复合酵母菌固态发酵动力学模型的建立

■ 王 勇 张锦玲 张立明 郭 鹏 袁丽佳 刘大程

(1.内蒙古农业大学兽医学院，内蒙古呼和浩特010018；2.农业部动物临床诊疗技术重点实验室，内蒙古呼和浩特010018)

酵母菌在特殊的发酵工艺下能够产生多种营养活性物质，如葡聚糖、甘露聚糖、氨基酸、多肽、有机酸等，这些营养活性物质在调控瘤胃功能和提高反刍动物免疫功能方面发挥积极的功效[1-2]。但前期科研工作中也发现，复合酵母菌培养物在固态发酵过程存在着缺陷：培养物中活性物质的产生规律及含量不清楚；发酵工艺多依靠技术工人的经验来控制，缺乏科学数据的支持；发酵结束后复合菌培养物质量的均一性较差，产品质量不稳定。

现阶段，对固态发酵动力学模型的研究大多在实验室条件下进行，且以β-葡聚糖、甘露聚糖为产物建立动力学模型研究鲜见报道，菌体生长动力学模型建立时，多以测定菌体细胞组分含量为主，如葡萄糖胺[3]、核酸[4]和麦角固醇[5]，但这些方法通常较复杂，且发酵基质成分对结果也可能会产生干扰[6]。M.R.Terebiznik等[6-8]通过测定发酵过程中发酵料干重的变化成功建立了估算发酵不同阶段菌体生物量的数学模型。

综上所述，本研究建立的动力学模型以生产实际为基础，通过测定发酵基质干重的变化估算菌体生物量，建立菌体生成动力学模型，以β-葡聚糖、甘露聚糖为活性产物建立产物生成动力学模型，应用这些模型对发酵工艺进行优化，对发酵过程进行预测及控制，为生产优质绿色饲料添加剂提供有力的理论基础。

1 材料与方法

本研究分别于2014年9月、10月和11月在内蒙古自治区呼和浩特市某生物科技有限公司发酵车间进行。

1.1 材料与仪器

酿酒酵母菌（Saccharomyces cerevisiae，SC）BC株、XR4株，均来源于内蒙古农业大学兽医学院反刍动物微生态制剂项目组菌种库；酵母菌活化培养基、麦芽汁培养基来自广东环凯微生物科技有限公司；固态发酵培养基[9]：培养基的基质成分及配比为麸皮52.69%、玉米片20.45%、玉米粉16.07%、米糠 4.09%、棉粕1.86%、豆粕 3.99%和无机盐 0.85%；β-葡聚糖、甘露聚糖、铅化玻璃珠(粒径0.45～0.6 mm，英国Sigma-Aldrich公司)。

安捷伦LC1100液相色谱仪（原产地美国）、T6系列紫外可见分光光度计（北京普析通用仪器有限责任公司）、Thermo Scientific生物安全柜（原产地德国）、HPS-160恒温生化培养箱（哈尔滨市东联电子技术开发有限公司生产）、Sigma 2-16pk高速低温冷冻离心机（SIGMA公司）、Sartorius精密电子分析天平（德国赛多利斯公司生产）。

1.2 试验方法

试验菌种制备：取 4℃ 保存的BC、XR4斜面菌种3环，接种于含有300 ml无菌麦芽汁培养基的1.5 L三角瓶中，于30℃、180 r/min摇床培养24 h后接种于50 L液体发酵罐中，30℃、180 r/min转速下培养48 h。

固态发酵：发酵料水质量比为1∶0.52，充分搅拌后，将混合好的发酵料堆放于发酵池（2 m×1.5 m×1.5 m）内，料高55 cm。

1.3 分析方法

1.3.1 采样

用采样器每隔3 h从固态发酵料表层下15～20 cm处均匀取样100 g，纬线圈法[10]取样225 g，混合均匀后，平均分为9份，3份样品用于测定干重，3份样品用于测定葡聚糖和甘露聚糖，剩下3份在80℃条件下烘干至恒重，用于测定底物总糖。

1.3.2 底物干重测定

称取不同时间的样品16 g，80℃烘干至恒重，称重[7]。

1.3.3 葡聚糖和甘露聚糖含量的测定

酵母破壁：涡流微珠破壁法[11]。

收集多糖：处理后的样品用冷却的去离子水充分清洗，收集玻璃珠，并收集洗液，重复5次。沉淀物加入3 ml去离子水，充分振荡，收集洗液，重复5次，合并洗液。将所得液体55℃静置24 h蒸发水分[12]。

酸水解：72%(w/w)的硫酸溶液进行酸水解[13]。

单糖含量测定:采用液相色谱-示差折光检测器测定样品及校正多糖中甘露糖和无水葡萄糖含量[14]。

结果计算:以校正多糖的含量为横坐标，峰面积为纵坐标制备校正曲线，得出回归方程。样品的峰面积代入回归方程中计算得到酵母β-葡聚糖及甘露聚糖含量。

1.3.4 底物总糖测定

采用硫酸蒽酮法测定底物总糖[15]。

2 结果与讨论

2.1 菌体生长动力学模型的建立

2.1.1 底物干重变化与菌体生物量关系的确定在固态发酵过程中，将底物烘干后，底物组成为[8]：

式中：W——发酵料干重(g)；

S——固态基质干重(g)；

B——菌体生物量（g）；

P——产物质量（g）；

dW/dt——发酵料干重变化率（g/h）；

dS/dt——固态基质消耗速率（g/h）；

dB/dt——菌体生长速率（g/h）；

dP/dt——产物生成速率（g/h）。

在固态发酵过程中，底物的消耗主要由于菌体生长、维持菌体生长和生成产物造成[15]，因此，可将式（2）变换为：

其中：

式中：(dS/dt)g——菌体生长消耗固态基质速率(g/h)；

(dS/dt)m——菌体维持消耗固态基质速率（g/h）；

(dS/dt)p——产物生成消耗固态基质速率（g/h）；

Yg——菌体生物量相关系数；

Yp——产物生成相关系数；

-km——维持菌体相关系数。

通过式（1）～（6）可得出底物干重与菌体生物量的关系：

其中：

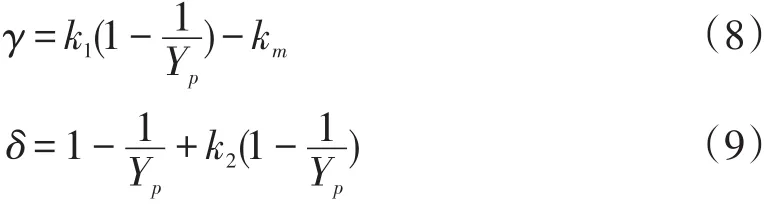
式中：γ、δ、k1和k2均为方程常数。

由Borzani等研究[8]可知，固态发酵过程中底物干重变化主要可分为2个阶段，结合图1、图2中底物干重变化可知，0～21 h为第1阶段，21～30 h为第2阶段，方程分别为：

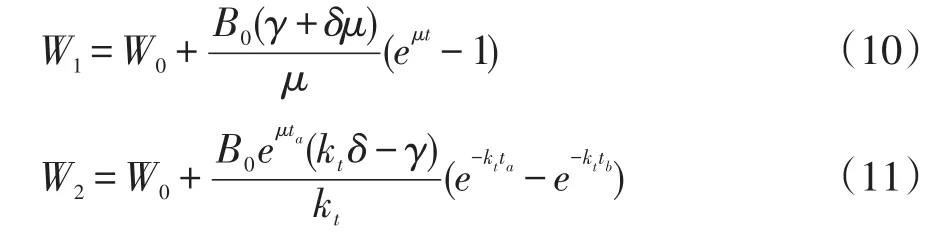
式中：W1——第1阶段发酵料干重（g）；

W2——第2阶段发酵料干重（g）；

W0——发酵料起始干重（g）；

B0——初始菌体生物量（g）；

μ——菌体生长比生长率（h-1）；

t——发酵时间（h）；

ta——第1阶段结束时间（h）；

tb——第2阶段结束时间（h）；

kt——方程常数。

由式（7）～（11）可得底物干重的变化与菌体生物量的关系式：

式中：Bs——不同时间菌体生物量（g）。

将底物干重结果带入式（10）和式（11）中，利用Origin 8软件进行曲线拟合，不同阶段拟合曲线见图1和图2，拟合方程式：

方程（13）和（14）的R2分别为0.974 9和0.929 9,方程均极显著（P＜0.000 1），表明方程计算所得干重值可以分别解释第1阶段97.49%的干重变化和第2阶段92.99%的干重变化，曲线拟合度较好。

由式（10）、（12）、（13）和（15）可得第1阶段菌体生物量的表达式：

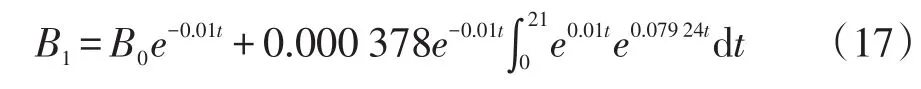
由式（11）、（12）、（14）和（16）可得第2阶段菌体生物量的表达式：

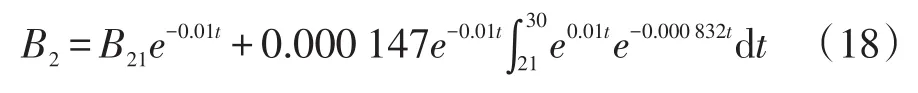
图1 第1阶段干重变化拟合曲线

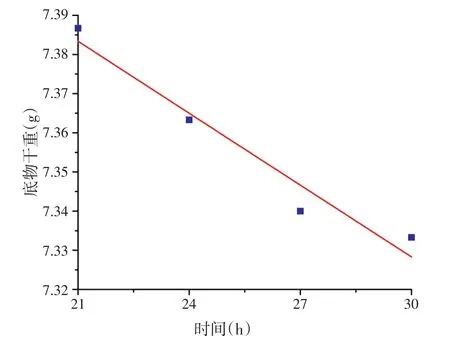
图2 第2阶段干重变化拟合曲线

2.1.2 Logistic模型的建立

Logistic模型是一个典型的S型曲线，通常被看作是一个表现细胞生长与营养物质之间的非线性关系的经验方程，能很好地反映该过程中菌体浓度增加对自身生长的抑制作用[16]，因此，采用此模型描述复合酵母生长动力学特性，Logistic方程[17]：

式中：Bm——最大菌体生物量（mg/g）；

μm——菌体生长最大比生长率（h-1）。

通过方程（17）和（18）计算所得生物量数据利用Origin 8软件进行拟合，参数估计值见表1。

表1 Logistic方程参数估计值

则复合酵母菌固态发酵菌体生长动力学模型为：

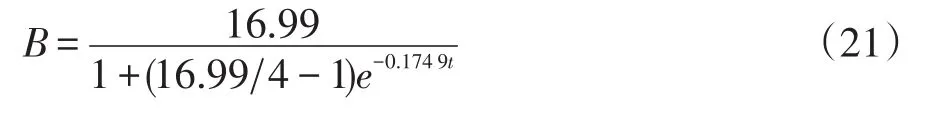
方程(21)的R2为0.959 8，方程极显著（P＜0.001），表明方程曲线拟合度较好，可以描述复合酵母菌在发酵过程中的生长情况。

2.2 产物生成动力学模型的建立

本研究用Luedeking-Piret方程来描述β-葡聚糖、甘露聚糖和菌体生长的关系[18]，即：

α、β为动力学参数，当α=0，β≠0时，产物生成与菌体生长为非偶联型；α≠0，β≠0时，产物生成与菌体生长为部分偶联型；α≠0，β=0时，产物生成与菌体生长为偶联型。本研究中，β-葡聚糖和甘露聚糖为酵母细胞壁的主要成分，其中β-葡聚糖为酵母细胞壁的主要多糖[19-21]，由于以β-葡聚糖和甘露聚糖建立Luedeking-Piret方程研究较少，因此，对模型的建立进行分类讨论。

①假设β-葡聚糖和甘露聚糖的生成模型为偶联型，即当β=0时，式（22）可简化为：

当t=0时，P=P0，将方程(19)带入方程(23)中，可得：

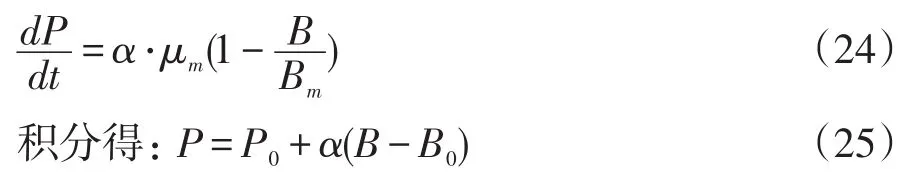
将不同时间点葡聚糖和甘露聚糖含量的P、B，以及P0、B0带入式（25）中，在软件1stOpt15PRO中利用Levenberg-Marquardt法和通用全局优化法求回归系数，可得：α1=4.09，α2=1.27。

②假设β-葡聚糖和甘露聚糖的生成模型为部分偶联型，即β≠0，

当t=0时，P=P0，将方程(19)带入方程(22)中，可得：

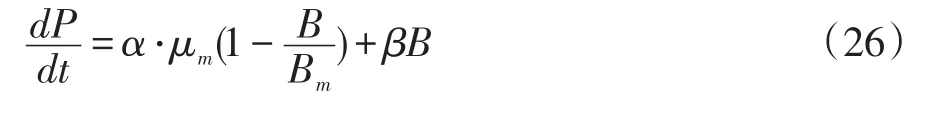
积分可得：

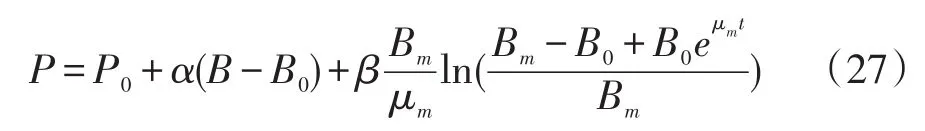
式中：P0——起始产物质量（g）。

将不同时间点葡聚糖和甘露聚糖含量的P、B以及P0、B0带入式（27）中，在软件1stOpt15PRO中利用Levenberg-Marquardt法和通用全局优化法求回归系数，可得：α1=5.083 5，β1=-3.23×10-5；α2=2.38，β2=-2.17×10-4。

由于β1和β2的值近似为0，因此，可知两种产物的生成与菌体的生长为偶联型，则可得：

β-葡聚糖生成模型：

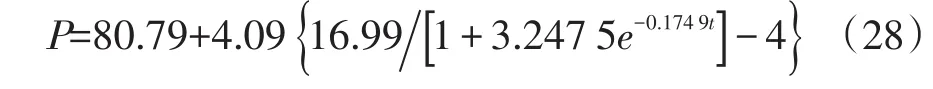
甘露聚糖生成模型：

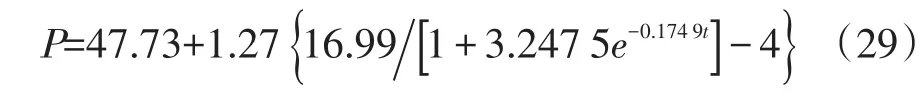
方程（28）和（29）R2分别为0.913 0和0.906 5，方程均极显著（P＜0.000 1），表明所选方程可以较好的反映产物生成的实际情况，相关性结果见图3和图4。

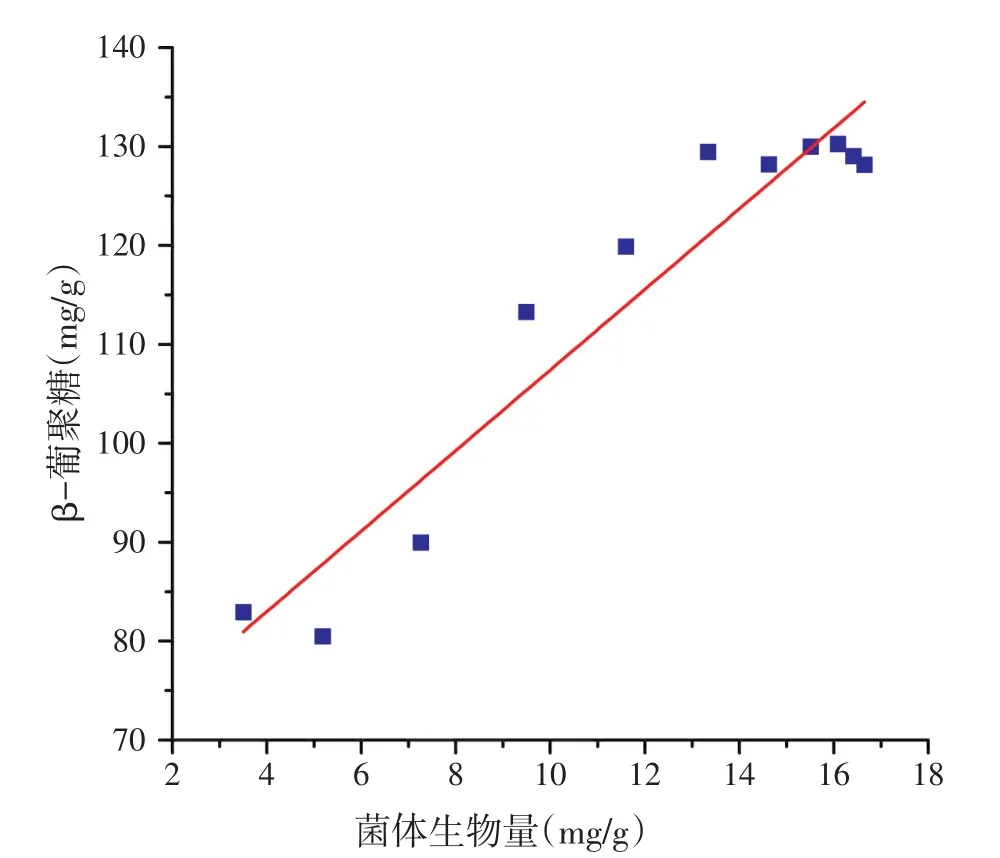
图3 β-葡聚糖生成与菌体生物量相关性

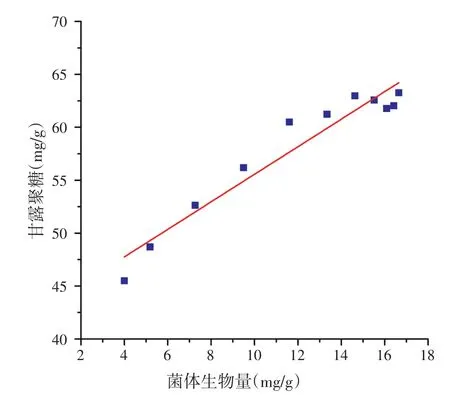
图4 甘露聚糖生成与菌体生物量相关性

2.3 底物消耗动力学模型的建立

常用的底物消耗动力学模型是基于底物消耗物料恒算建立的Luedeking-Piret/like方程式[22]，即：

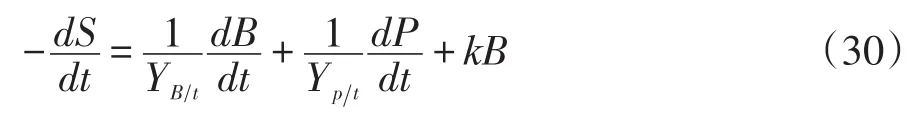
式中：St——底物总糖含量（mg/g）；

St0——起始底物总糖含量（mg/g）；

YBt——总糖用于菌体生长的得率常数；

k——维持常数。

酵母发酵过程中，总糖的消耗与产物合成仅有间接关系，假设基质的消耗用于产物合成的比例很小，可忽略不计，认为总糖的消耗仅用于菌体的生长，所以式（30）可简化为：

将式（19）带入式（31）积分得：

将不同时间点的B、St和B0带入式（32）中，在软件1stOpt15PRO中利用Levenberg-Marquardt法和通用全局优化法求回归系数，可得：YBt=0.112，S0=128.12。

则可得底物消耗动力学模型为：

方程（33）R2为0.949 6，方程均极显著（P＜0.000 1），表明所选方程可以很好的反映底物消耗的实际情况，相关性分析见图5。

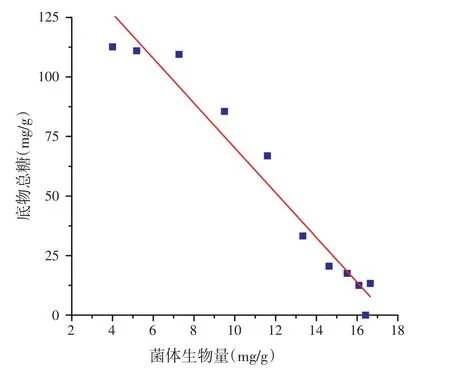
图5 底物总糖消耗与菌体生物量相关性

2.4 模型准确性分析

为了验证模型的准确性，在相同条件下进行复合酵母菌固态发酵的重复实验3次，实验结果取平均值，与动力学模型计算值进行比较，结果见表2。

表2 复合酵母菌固态发酵菌体生物量、甘露聚糖含量、β-葡聚糖含量和底物总糖含量动力学模型理论值与实际值对比

由表2可知，发酵料干重、甘露聚糖含量、β-葡聚糖含量和底物总糖含量的相对误差基本都小于10%，说明建立的动力学模型能较好地描述生产实际中复合酵母菌固态发酵过程。

3 结论

①以固态发酵料干重变化为基础建立了复合酵母菌菌体生物量生长Logistic动力学模型，B=方程极显著（P＜0.001），通过模型验证，干重模型平均相对误差为0.94%，间接表明在生产实际中复合酵母菌的生长符合Logistic方程。

②通过对Luedeking-Piret方程参数α和β分类讨论并计算，发现β-葡聚糖与甘露聚糖的生成与酵母菌为偶联型，其中β-葡聚糖生成模型P=80.79+4.09甘露聚糖生成模型P=R2分 别 为0.913 0和0.906 5，平均相对误差分别为4.71%和3.7%，方程均极显著（P＜0.000 1）。底物消耗动力学模 型R2为0.949 6，平均相对误差为6.63%，方程极显著（P＜0.000 1），说明模型可较好地描述发酵过程，对优化实际生产工艺，控制和预测发酵过程具有重要的参考价值。