两电机同步系统支持向量机广义逆控制
2015-01-21仲伟松张贞艳
张 锦,仲伟松,张贞艳,高 磊
(宿迁学院,江苏 宿迁 223800)
0 引言
多台交流电机同步调速系统在冶金、纺织、造纸等行业中应用广泛,但这类控制的高阶、非线性、强耦合问题如何解决是当前研究的瓶颈[1]。
逆系统是一种直接反馈线性化方法,已具备较完善的理论体系。但其要求模型精确可知,按照传统逆系统方法得到这类非线性系统的数学模型较困难。因此有学者提出基于神经网络[2]构建逆系统的方法来解决此问题,收到一定的效果,却同时存在过学习、过拟合等不足。而支持向量机[3]处于小样本情况时,可解决这类缺陷。因此采用支持向量机来逼近原系统的逆系统,串接于原系统前构成复合伪线性系统,从而完成系统的解耦与线性化。因为构建的逆系统难免会有一些建模误差,所以选择PID 控制器[4]以确保系统的鲁棒性。
本文以两电机同步系统为研究对象,将由支持向量机辨识的广义逆模型和PID 控制相结合,并对其控制效果进行仿真验证研究。
1 两电机系统支持向量机广义逆模型
1.1 两电机同步系统数学模型
图1 为两电机同步系统转速与张力控制结构示意图。

图1 两电机同步系统结构示意图Fig.1 Control diagram of two-motor synchronous system
基于矢量控制方式下且磁通稳定时,其数学模型可简化为[5]:
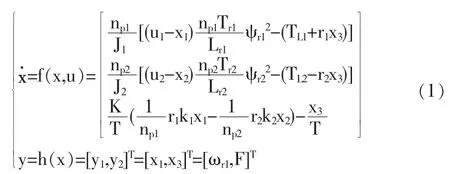
式中: 下标1、2 分别表示第1、2 台电机。k,r 分别为皮带轮的速比、半径;J—转子转动惯量;ω—定子频率的同步角速度;TL—负载转矩;Tr—电磁时间常数;ψr—转子磁链;Lr—转子自感;ωr—电气角速度;K—传递函数;T—张力变化常数;np—电机的极对数;皮带的张力为F。其中状态变量x=[x1, x2, x3]T=[ωr1, ωr2, F]T;控制变量为u=[u1, u2]T=[ω1, ω2]T。
1.2 广义逆的实现
将式(1)中输出求导,得其Jacobi 矩阵为:
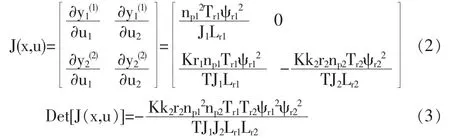
根据广义逆理论[6],系统的向量本阶性为3,而系统的相对阶为α=(1,2),即阶数为α1+α2=3,因此系统的本阶性等于向量相对阶,可知此系统可逆。由此系统的广义逆可表示为:


2 支持向量机
支持向量对比与神经网络控制算法差异在于采用了结构风险最小化原则。支持向量机能够很好地避免小样本情况下存在的过拟合等缺陷。其核心思想为将函数集构造成为一个函数子集序列,子集间折中取值经验风险和置信范围,以达到实际风险最小。其基本表达式为[7]:

式中:(·)是内积,w∈Rd,w —权系数;b—域值。在线性不可分条件下,综合考虑最大分类间隔及最小化分类误差,在式(6)基础上考虑松弛变量ξi≥0 求:
其中: C 表示惩罚因子,即将目标改为求此二次规划问题。
3 支持向量机广义逆PID 控制策略
首先构建由支持向量机辨识的原系统 (两电机同步系统) 广义逆模型: ①向原系统给定足够的激励信号;②取原系统的输出作为支持向量机逆系统的输入,而原系统输入作为支持向量机逆系统的输出,并对采样信号进行归一化处理;③支持向量机的核函数取高斯核函数,选择合适的核宽度及正归化系数等参数,得广义逆模型的输出。
将由支持向量机辨识的广义逆模型与以两电机同步系统为构成的原系统串接,从而行成复合伪线性系统。由式(6)可知,原系统转化为1/(s+1)的速度子系统及1/(s2+1.414s+1) 的张力子系统。
转化后的伪线性系统实现了原系统的解耦与线性化,但由于存在开环建模误差,此时引入PID 控制从而取得更好的闭环控制效果。PID 中比例、积分、微分环节系数需要根据实际控制效果调整,先确定合适的P 参数,然后调整I 及D 的参数,确定最佳PID 参数同步控制伪线性系统,从而构成了支持向量机逆PID 闭环控制系统。如图2 所示。
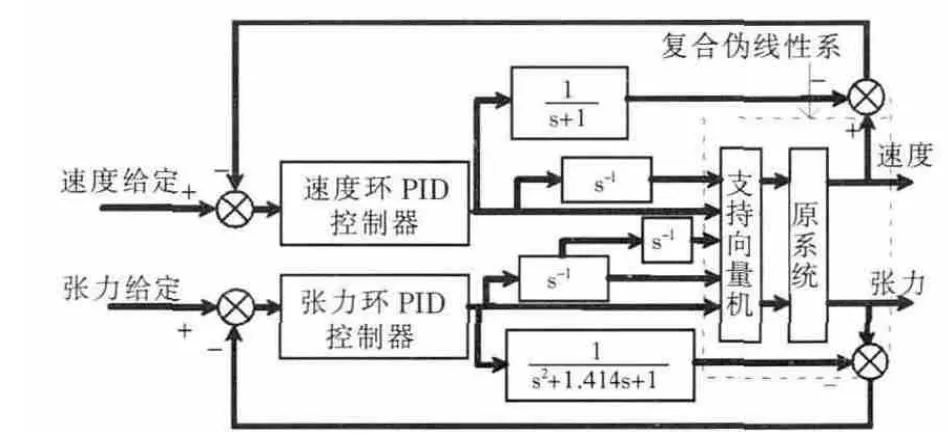
图2 支持向量机逆PID 控制原理图Fig.2 Diagram of SVM- PID control system
4 仿真验证
使用Matlab/Simulink 构建两电机变频系统模型并进行仿真。由支持向量机辨识两电机调速系统的广义逆模型,最后引入模糊PID 控制器实现闭环控制。
当转速给定250~350 r/min,张力给定300 N,图3~4 分别表示系统在传统PID 以及支持向量机广义逆与PID 方法结合后转速突增时的仿真试验波形。对比可看出,较传统PID 控制方法,支持向量机逆PID 算法更快地消除稳态误差,具有更好的鲁棒稳定性。
仿真结果证明了支持向量机逆模糊PID 控制策略的可行性。
5 结束语
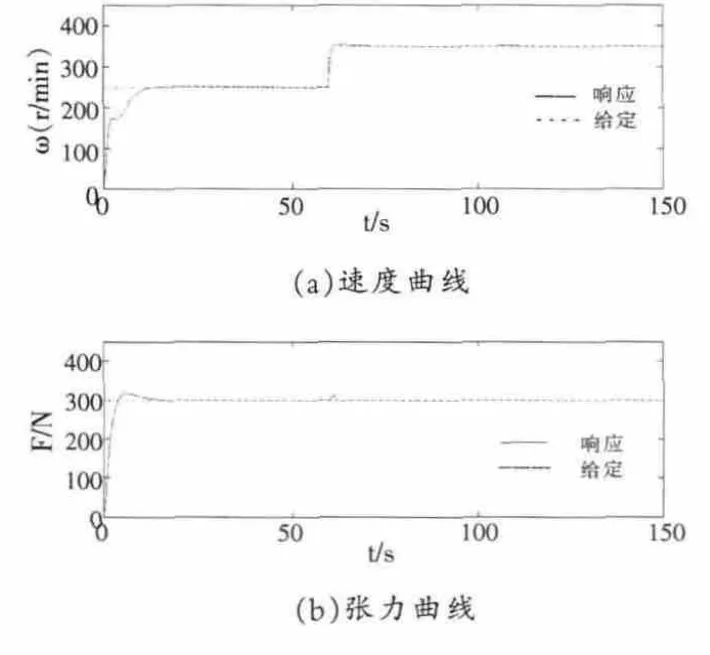
图3 PID 控制仿真响应波形Fig.3 Simulated responses with PID control

图4 支持向量机逆PID 控制仿真响应波形Fig.4 Simulated response with SVM- PID
针对两电机同步系统本文设计了由支持向量机逼近的广义逆模型与PID 相结合的控制方法。经过仿真及试验研究,可得出如下结论:
(1)支持向量机逆PID 控制不仅实现了两电机变频系统的解耦而且具有很高的控制精度。
(2)对比传统PID 方法,支持向量机逆PID 控制具有更好的动态响应特性。
[1] Hassan Kaghazchi,James Mannion.Synchronisation of a Multimotor Speed Control System [J].Assembly Automation,2013,4.
[2] 戴先中,刘国海.两变频调速电机系统的神经网络逆同步控制[J].自动化学报,2005,6.
[3] 王定成,方廷健,高理富,马永军.支持向量机回归在线建模及应用[J].控制与决策,2003,1.
[4] 吴宏鑫,沈少萍.PID 控制的应用与理论依据[J].控制工程,2003,1.
[5] 张懿,刘国海,魏海峰,等.基于最小二乘支持向量机左逆的两电机变频调速系统张力辨识策略[J].中国电机工程学报,2010,30.
[6] 刘国海,张锦,赵文祥,张懿,蒋彦.两电机变频系统的支持向量机广义逆内模解耦控制[J].中国电机工程学报,2011,6.
[7] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,1.
