关于矿物元素配合物生物学效价估计方法
2015-01-21王继华
■王继华 刘 伯
(河北工程大学动物科学系,河北邯郸 056002)
动物营养和饲料研究主要是动物对养分的需要量,这与饲料质量有关,传统上就是研究饲料的生物学效价,矿物元素配合物也不例外。
1 矿物元素配合物生物学效价的概念
Kirchgessner(1974)将必需微量元素的总利用率定义为吸收率与代谢率的乘积。一般养分的吸收率与利用率可按下列公式计算:
真吸收率(%)=[I-(F-M)]/I×100;
利用率(%)=[I-(F-M)-(U-E)]/[I-(F-M)]×100。
式中:I为食入某养分的量(g);F为粪中某养分含量(g);M为粪中代谢来源某养分含量(g);U为尿中某养分含量(g);E为尿中内源的某养分含量(g)。
为此,必须将粪中某养分是来自食物,还是来自体内代谢,尿中某养分是代谢的,还是内源的,加以清楚区分。然而,有很多因素影响微量元素吸收及在粪尿中的内源排泄量。因此,上述方法不仅复杂,有时甚至不能应用。
Ammerman(1995)定义生物学效价(bioavailabili⁃ty)为吸收后的营养素中能被动物利用的比例。Greger(1992)指出这一概念反映的是所有影响营养素吸收、转运、贮存和排泄的因素(日粮和非日粮的)的综合效应。Gueguen(1995)更明确指出,一种养分的生物学效价是指动物食入的养分中能被小肠吸收并能参与代谢过程或贮存在动物组织中的部分占食入总量的比率。可以看出,生物学效价与总利用率是两个近似的概念。
2 估计矿物元素生物学效价的方法
可用于研究矿物元素生物学效价的技术很多,可分为体外研究和动物饲养试验。体外研究(in vitro studies)更省钱,允许对试验变量做更多控制。体外研究的主要缺陷是不能模拟那些影响矿物元素生物学效价的生理状态或某些物理、化学性质和适应性反应。虽然已开发出最新的方法试图纠正这些限制和小肠吸收条件,然而,动物饲养试验对估计营养物质的生物学效价往往更实用。
评定矿物元素生物学效价的方法主要有绝对效价法和相对效价法。其中相对效价法主要是指相对生物学价值,历来美国NRC标准中的矿物质饲料营养价值的讨论引用的多为该方法测定的结果。绝对效价法包括表观消化率法、真消化率法以及体外消化法等。其中,相对生物学价值、表观消化率和体外消化法都不能反映动物对矿物元素吸收利用的真实情况,这是造成矿物元素盲目添加、过量排泄、污染环境的原因之一。矿物元素的真消化率能反映动物对矿物元素真实的吸收利用情况,许振英(1986)指出,矿物元素具有内源代谢粪的损失,其实还可能有尿中的损失,尤其是钙、磷、镁和铁,因此测定他们的表观消化率意义不大,重要的是测定真消化率。由于受矿物元素内源损失的干扰,至今尚无理想的测定方法。
就发表的研究论文看,无论是有机微量元素(包括铜、锌、铁、锰、硒等)还是无机微量元素,生物学效价研究方法大体上可分为三类:平衡试验法、放射性同位素法和斜率比法。
平衡试验法通过测定食入量、粪及尿排出量和内源损失量,以食入量减去粪中排出量计算表观消化率,即表观消化率(%)=(进食量一粪中排出量)/进食量×100。在此基础上再扣除尿中排出量计算表观代谢率,即表观代谢率(%)=(进食量一粪中排出量一尿中排出量)/进食量×100。这种方法相对快速、简便,但由于受微量元素内源损失的影响,无论是表观消化率还是表观代谢率,都不能反映其真正利用率。要测定真利用率,就需要使用纯合或半纯合日粮,不仅成本高,同时环境中的微量元素也会严重影响测定结果。因此用这种方法测定不同来源微量元素生物学利用率的试验报道不多。总之,当粪中某元素的内源排泄量不定时,作为总利用率的两个因素之一的吸收率,即无法用常规平衡试验测定,大多数微量元素属于此种情况。微量元素吸收后的代谢效率的直接测定更为困难,尤其是因为必需微量元素涉及许多代谢功能。因此,实践中经常设计间接方法,例如用各种耗竭再补偿法。
测定真吸收率的一个直接方法是同位素稀释法,试验动物经过一定时间的耗竭,在试验开始时,喂给各组动物不同数量的待测元素,同时注射一次一定剂量的该元素的放射性同位素。然后,连续定时测定血液、各种组织、器官和粪、尿中稳定的和放射性的微量元素含量,直至它们达到平衡。根据稳定的与放射性微量元素的比例,可以算出粪尿中微量元素的内源排泄量及该元素的利用率。放射性同位素法是通过测定标记微量元素在体内组织中的存留量来测定微量元素的利用率,可以反映微量元素在体内的分布情况,从理论上讲最理想,但要求一定设备,饲料成本也高,虽然在测定饲料原料中矿物元素生物利用率方面应用广泛,但在有机微量元素利用率测定方面应用不多。
总之,用同位素示踪法测定矿物元素的相对生物学效价,试验周期更短,一般不需要2~4周时间,但耗资更大,对小动物试验来说不太经济,而且用同位素示踪测定矿物元素表观消化率意义不大,因为粪中排出的矿物质既混有未吸收的,也有内源性的。
相对生物学效价(the relative biological efficacy,RBV)的测定方法一般采用斜率比法。通常采用耗竭-补偿法(depletion-repletion)来研究养分的生物学效价,以铁为例,先饲喂动物缺铁日粮,使动物体内铁贮适度耗竭后(血红蛋白含量下降),再饲喂不同水平铁的日粮,选择敏感的判据指标(生产性能、组织器官铁浓度、酶活等)来估计铁的生物学效价。每一种铁源为一个因子(其中一个应用最广泛的铁盐为参照物,例如硫酸亚铁),每个因子设置不少于4个水平,针对每一种铁源估计组织存留量(依变量y,mg/kg)对日粮铁含量(自变量x,mg/kg)的回归方程,用待测铁源的回归系数与标准参照铁源的回归系数之比(%)作为待测铁源的生物学效价,是待测铁源相对于参照铁源的生物学效价,正如Steike等(1978)给出的定义式,这就是所谓的斜率比(slope ratio)法。
3 斜率比法和平行线法
斜率比法在矿物元素的生物学价值评定方面应用最广。其优点在于:相对生物学效价(RBV)法忽略了动物矿物元素利用过程的许多问题,比较看重结果而不太注意过程,不但简化了试验过程,而且试验结果在实际生产上也具有实用性。斜率比法不足之处:①由于没有一个统一的反应指标和标准参照物,使得不同研究结果差异较大,相互之间缺乏可比性;②由于无机矿物元素盐的性质相对稳定,但植物性饲料受品种、气候、地理条件等多种因素影响,试验结果重复性较差;③斜率比法测定方法比较复杂,一般需要配合进行屠宰试验,试验成本较高。
回归线斜率比方法的原理是基于几个假定。首先是假定在待测矿物元素配合物和标准参照物,自变量与依变量之间都是直线关系,待测矿物元素配合物的回归方程是y=at+btx,标准参照物的回归方程是y=as+bsx,见图1。进一步的假定是两种物质在x=0时反应相当,也就是两条回归线在x=0处相交,at=as,所以可把截距值用一个共同数值表示为a,结果是,待测矿物元素配合物的回归方程可表示为y=a+btx,标准参照物的回归方程可表示为y=a+bsx,于是,让xt和xs分别表示产生相等的y所需要的待测矿物元素配合物和标准参照物的数量,那么,a+btxt=a+bsxs,由此即可解出回归线的斜率比为:
RBV=xs/xt=bt/bs。
根据生物学效价的定义,这个斜率比就是待测物的生物学效价,这就是斜率比法这个名称的由来。估计量RBV很有价值,只是需要假定线性反应并且两条回归线相交。可用统计测验来检验这些假定是否成立,Finney(1978)给出了这些统计测验方法。一般软件都有这个分析程序,例如SAS的PROC GLM、SPSS软件,还可用于估计RBV的标准误。
根据多重线性回归模型原理,可以把全部试验数据用一个线性模型表示为:
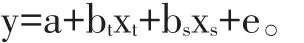
这样用一个模型表示并且使用多重回归方法分析试验数据,使得试验数据的统计分析更加明晰,统计分析的精度更高。

图1 斜率比法
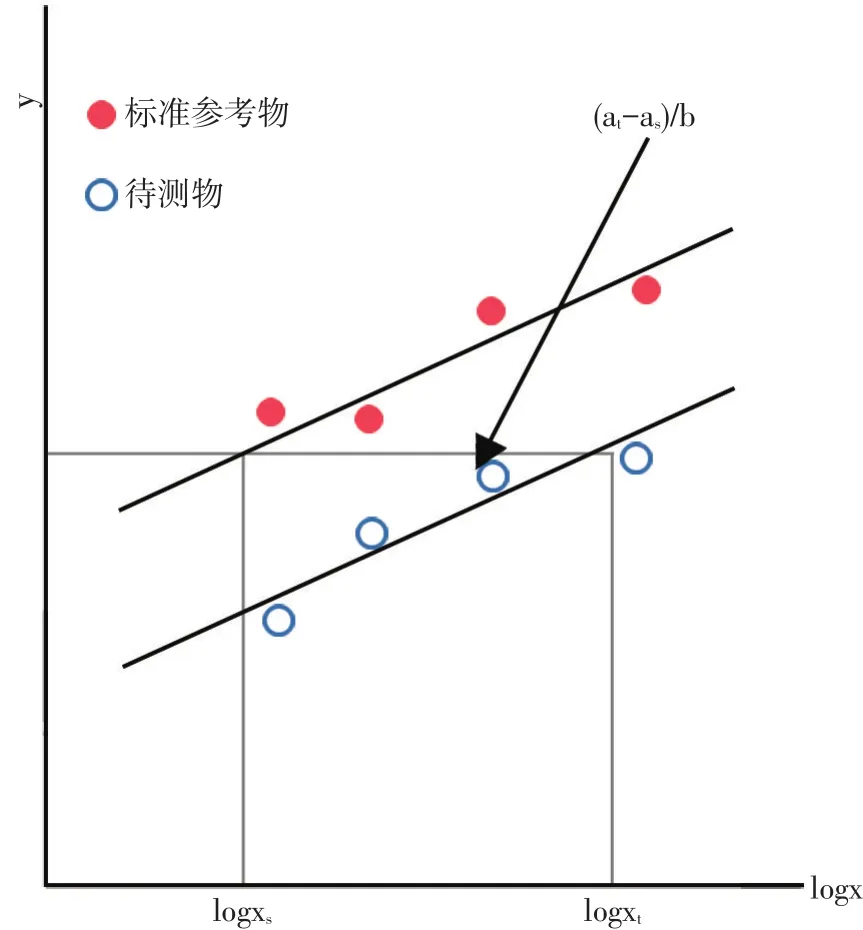
图2 平行线法
这样用一个模型表示并且使用多重回归方法分析试验数据,使得试验数据的统计分析更加明晰,统计分析的精度更高。
关于待测物与标准参照物的两条直线相交的假定一般是成立的,因为在x=0时,实际上就是基础日粮,饲喂待测物和参照物的两组动物都是使用的基础日粮,完全一样的日粮,所以应该有at=as。如果实践中at≠as,那就说明两组试验动物或饲养管理有差别,而不是饲料营养的差别。但是,关于自变量与依变量之间都是直线关系的假定未必成立,待测矿物元素配合物的回归方程未必是y=at+btx,标准参照物的回归方程未必是y=as+bsx,这个问题本文后面有进一步讨论。
Pott等(1999)曾用斜率比法测定无机钼对羔羊的生物学效价,标准对照物为试剂级钼酸钠,待测物分别是钼酸铵、三氧化钼和金属钼。分别建立了肝、肾、肌肉等组织沉积量(y)对日粮不同钼源添加量(x)的回归方程,然后用不同钼源方程的斜率与标准对照物钼酸钠的回归方程的斜率之比估计了不同钼源的生物学效价。
Huang等(2013)通过不包括两个对照组的2×2×4三因素方差分析设计,测定了不同锌源在肉鸡的生物学效价。一个因子是日粮植酸含量,分为高与低2个水平;一个因子是日粮植酸添加量,分为高与低2个水平;一个因子是日粮添加不同锌源(1个硫酸锌和3个有机锌),每个锌源添加量分为高与低2个水平。使用SAS(1988)的混合程序,笼为试验单元(每笼10只肉鸡),18个处理,每个处理6个重复。数学模型包括植酸水平、各种锌源锌水平的主效应,与全部适当的交互作用。检测到的统计学显著的效应,用Tukey-Kramer多重比较检验处理均数。对照组(空白对照NC和标准对照物对照PC)与试验组(补充锌)的比较是采用单一自由度正交对照分析法。比较同一植酸水平内不同锌源的线性回归斜率(Littell等,1995,1997),斜率比及其标准误差使用误差传播法(Littell等,1995)估计。不同锌源之间的差异使用最小显著差数(LSD)法测定各回归系数的差异(Huang等,2009)。
矿物元素的浓度与反应变量的关系,有时候y对x的对数呈线性关系。标准参照物回归方程是y=as+bsLog10x,待测物是y=at+btLog10x。如果这2条回归线斜率相等(平行线),那么,标准参照物和待测物的回归方程分别变为y=as+bLog10x和y=at+bLog10x,于是可有as+bLog10x=at+bLog10x,由此解出 Log10(xs/xt)=(at-as)/b。所以RBV估计值为RBV=antiLog[(at-as)/b]。从几何学来看,RBV就是一个水平线段的反对数,这个线段就是平行于横坐标的那条直线被两条平行线截断的这一段,如图2中箭头所指,所以,这种方法又叫平行线(parallel lines)法。
4 影响生物学效价评估结果的因素
用斜率比法研究矿物元素配合物的相对生物学效价有大量报道,但结果差异很大。影响生物学效价的主要因素,可分为动物因素、矿物元素本身、待测元素的生理学、试验设计技术、饲料和饲养管理等。
4.1 动物因素
①受试动物物种(单胃、反刍、家禽)、年龄、性别、生理状态(生长、怀孕、泌乳);②体质与健康状态。③受试动物体内矿物元素贮存状况;包括数量与化合态;④动物对于被测营养素的缺乏要有敏感的反应;在开始阶段,体重的变异应尽可能小(变异系数CV<5%);⑤动物生产性能对待测矿物元素的反应呈速度递减规律,与梯度添加试验结果相吻合,符合反应+平台的数学模型。
4.2 矿物元素本身因素
①矿物元素的化学形式(无机盐或配合物);②这个矿物质配合物的溶解度;③吸收的磷酸钙,硅酸盐,日粮纤维等;④矿物元素的电子结构和竞争性拮抗,不同化学态及价态的矿物元素在动物体内的代谢途径不同,会严重影响其生物学效价;⑤配位数(Coordi⁃nation number);⑥给药途径(口服或注射);⑦配合物等螯合剂的存在与否;⑧待测元素形成矿物元素配合物的能力,包括理论(体外)预测和有效(体内)能力;⑨其他矿物元素的相对数量,尤其是有协同作用或拮抗作用的;⑩矿物元素配合物产品质量。
4.3 待测元素的生理学因素
①与天然配体(ligands)的相互作用:包括蛋白质、肽、氨基酸,碳水化合物,脂质,阴离子分子,其他金属元素。②待测元素存在或穿过肠道黏膜时金属运输配体的竞争(Competition with metal-transporting ligands);吸收后内源性载体配体(Endogenously medi⁃ating ligands);和释放到靶细胞的过程。
4.4 试验设计技术因素
①试验设计时所设定的矿物元素添加水平,额外添加的待测矿物元素的量要占基础日粮中该种元素含量的主要地位。一般认为,添加的待测元素与基础日粮中该元素含量之比越宽,这项试验对于待测矿物元素配合物的反应就越敏感。②待测元素添加水平应在4个或以上,而且添加水平应使日粮总水平不超过动物的营养需要量,也就是每一个水平都低于动物的营养需要量;而且大部分的添加水平应在敏感范围之内;每个处理至少应有5个重复。③研究中所用评价指标:家畜不同组织器官的沉积量不同。④试验研究持续的时间。⑤试验技术,主要有:a)应用正确的研究设计;b)选择应用标准试材;c)应用正确的观察测定数据和记载;d)充分利用控制条件;e)多学科联合,综合研究;f)应用现代技术和设备,改进研究方法;g)对试验观测结果的正确分析方法。
4.5 饲料因素
①日粮结构,日粮组成应接近生产实际;根据原材料的实际分析值调整配方;②研究中所用日粮类型,基础日粮中待测元素含量和添加量;③添加的待测矿物元素配合物必须充分混匀(分析结果为准)。
5 剂量-反应模型
Littell等(1997)曾介绍动物营养报酬递减定律,也就是剂量反应曲线。一般情况下,动物性能表现(反应,依变量y)与日粮中某一养分的浓度(剂量,自变量x)之间的关系是一条指数-平台曲线(见图3),所以要对依变量y进行对数转换(而不是对自变量x进行对数转换),转换后的数据才可以进行回归分析。
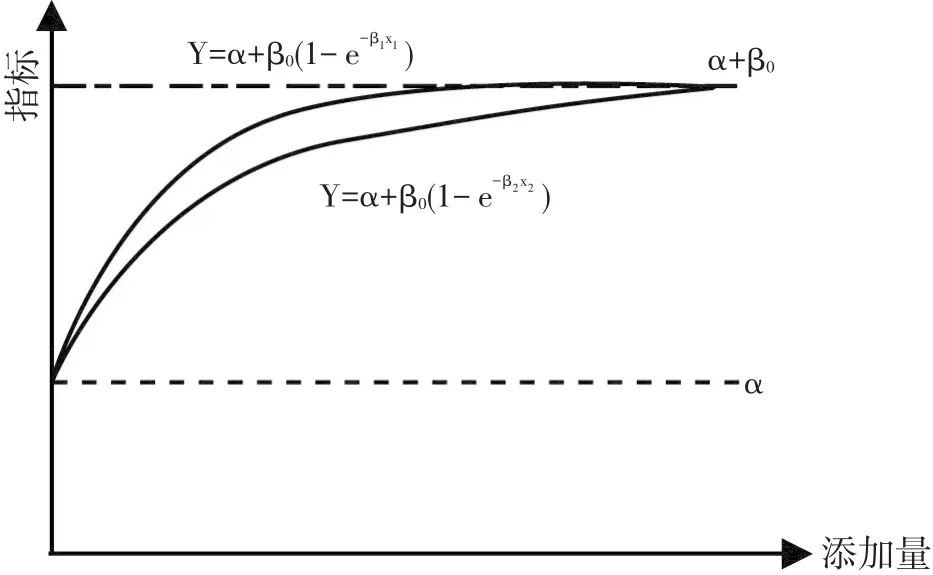
图3 动物营养报酬递减定律
待测元素的指数方程为y=α+β0(1-exp(-βtxt);
标准参照物的方程为y=α+β0(1-exp(-βsxs)。
式中:y是指生产性能观测指标;α是截距(对照组数据);β0是渐近效应,α+β0是指共同的渐近线(生产性能极值);βt和βs分别是待测物与标准参照物的回归系数;xt和xs分别是待测物与标准参照物的添加量。
这里强调,实践中要检验待测物和标准参照物的方程中渐近效应β0是否相同。
待测元素相对于标准参照物的RBV按以下公式计算:

一般在同一饲养试验中基础日粮相同,如果设计试验时待测物与标准对照物水平个数相同,并且在每个水平上添加量都相等(一一对应),如图所示的试验(必要时可以不满足这个要求),则可用一个多重非线性回归模型—非线性同平台回归模型(The nonlinear common plateau regression model,NLCPR模型)表示整个试验数据(Schutte等,1996;Kratzer等,2006):
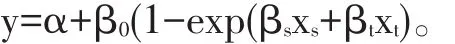
这一指数模型主要有3个特点:第一,标准参照物与待测物有不同曲线;第二,2条曲线始点相同(α);第三,2个曲线具有相同的渐近线(α+β0)(生产性能极值)。第二和第三个特点表明了待测物与标准参照物具有一个共同的出发点和一个共同的终点(平台),标准参照物与待测物的差别只在第一个方面,即,不同曲线到达渐近线的速度。实践中,这个指数模型可以使用SAS程序的PROC NLMIXED code运算。我们强调指出,①第三个特点未必为真,所以实践中可视为一个假设,分析试验结果前先对这个假设进行统计检验;②如果假设检验的结果是否定的,那么,可使用Kratzer等(2006)给出的模型。
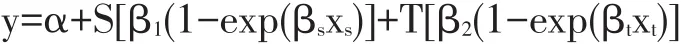
这里:S和T是只取0和1两个数值的变量,当反应值包含相应的矿物元素添加剂时,取值为1,否则为0。
Elwert等(2008)评定65%稀释DL-蛋氨酸的生物学效价,表明日粮中添加梯度与动物反应是指数回归关系(见图4)。所以,观测数据y要经过对数转换,才与自变量呈线性回归关系。Elwert等(2008)的指数回归方程为:

3种蛋氨酸添加剂DL蛋氨酸、稀释的DL蛋氨酸(65%)和蛋氨酸羟基类似物MHA-Ca的相对生物学效价计算式分别为:DLM=23.0/23.0=1,DLM(65%)=13.9/23.0=61%,MHA-Ca=14.9/23.0=65%。
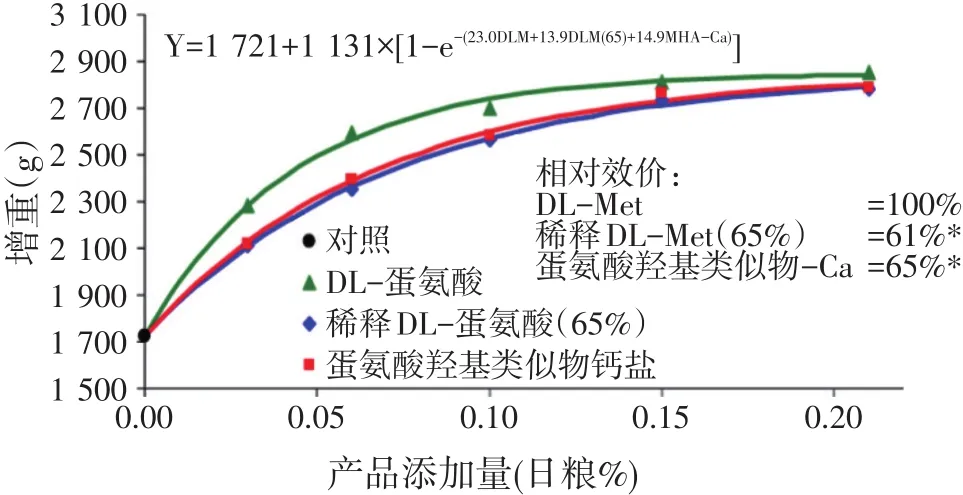
图4 添加剂的梯度添加和指数回归反应
因此,实践中应该先对依变量y与自变量x之间的关系进行检测,然后确定采用什么方法分析生物学效价。如果用线性回归模型处理指数回归问题,势必加大误差。
一般认为动物营养的剂量反应不是抛物线-平台曲线或指数-平台曲线,而是可以分为5个阶段的曲线,因为动物对某种养分的需要量有一个适中区,采食量过高或过低都不合适,表达这个现象一般用图5。
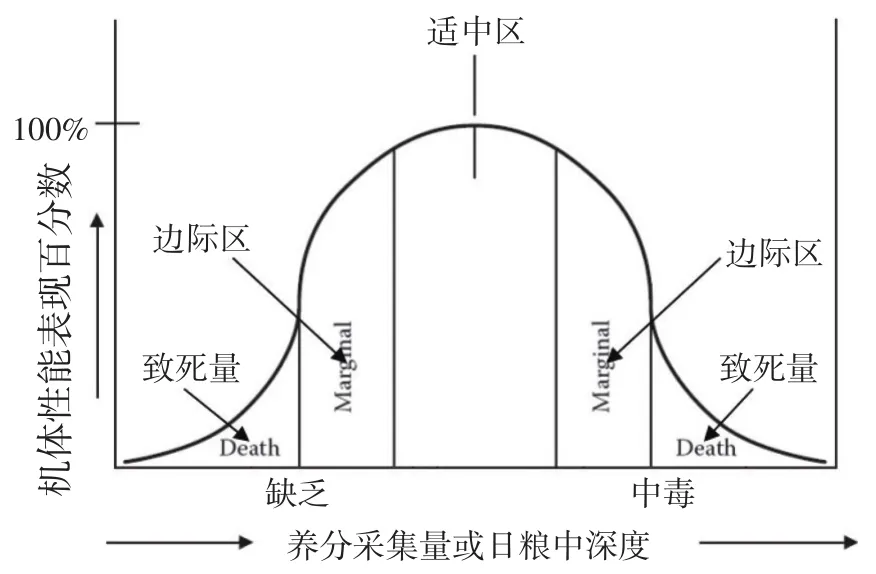
图5 对养分采食量的典型剂量反应
剂量反应曲线在各个研究领域都很常见。曲线的上升阶段和曲线顶部适于研究动物对某个养分的营养需要量,包括矿物质,蛋白质,能量,饲料效率等。这些试验研究的统计分析技术,突出表现为分段回归模型,包括折线回归模型,二次多项式+平台模型,抛物线+平台模型,指数-平台模型或其他非线性反应+平台模型。
