面向城市热环境格局时空演变的多重分形模式
——以郑州市为例
2015-01-20吴国玺杜根远李长坡申怀飞
高 歆,吴国玺,杜根远,李长坡,申怀飞
1 许昌学院, 城乡规划与园林学院, 许昌 461000 2 许昌学院,国际教育学院, 许昌 461000
面向城市热环境格局时空演变的多重分形模式
——以郑州市为例
高 歆1,*,吴国玺1,杜根远2,李长坡1,申怀飞1
1 许昌学院, 城乡规划与园林学院, 许昌 461000 2 许昌学院,国际教育学院, 许昌 461000
与单分形相比,多重分形模型赋予了更多描述客观世界中复杂现象和事物的参数和手段,为更加准确和精细地刻画自然界中普遍存在的非线性现象和过程提供了一种有效途径。以河南省郑州市为研究对象,选取三期Landsat5-TM影像反演城市地表温度,并采用多重分形的理论与方法定量地探讨和研究城市热环境场纹理结构及其在时空中的分布特征,以及在不同的标度区间内热环境场与NDVI之间的关系。研究结果表明:20年间郑州市热场景观的多重分形谱奇异性指数最大值与最小值之差α由0.6716减小为0.6419,奇异性指数最小值αmin和最大值αmax分别由1.4644、2.136减小为1.4304和2.0723,背景场奇异值α(fmax)由2.0111减小为2.0083,纹理测度最大值与最小值的分维数f(αmin)和f(αmax)分别由0.2354、1.4877增大为0.3412和1.734,意味着随着近20年经济的发展和城镇化率的提高,研究区域的热场纹理信息量不断减少,结构趋于简单,而纹理测度最大值、最小值和研究区温度有增大的趋势。对于位于郑州市不同位置且由不同景观斑块类型构成的区域,市区区域纹理测度波动幅度最小,而水体区域最大;市区纹理测度最大值和最小值的分维数最大,不同等级纹理像元数量分布比较均匀,空间簇聚程度高,而水体则相反,另从市区样本的多重分形参数来看,新开发的区域比老市区具有更小的αmin值和D2值。区域温度均值与多重分形参数之间呈现较强的线性相关性,而区域标准差与多重分形参数之间的相关性更强,线性变化的顺序依次为水体、农业用地、城郊和市区。另外,还利用C-A(浓度-面积)模型把2011年热场图像纹理结构分割为3个标度不变性区间,在此基础上讨论了奇异性指数α对区域温度与NDVI(归一化植被指数)之间关系的影响,发现斑块边缘的地表温度对NDVI最为敏感,且奇异性指数对不同标度区间的地表温度的本底值贡献是正向的,这些结论对热环境场的尺度转换研究具有一定的参考意义。
多重分形;热环境;格局;纹理;浓度-面积模型
随着城镇化速度的加快,城镇化的发展带来了剧烈的土地利用变化,大量的农业用地被城镇建设用地所取代,大量的生态环境问题也随之而来,其中,城市热岛效应已经成为全世界关注的焦点问题。城市热环境场是由复杂的地表景观格局及其热环境过程直接决定的,不仅受到地物本身热力学性质的影响,而且也受到地表环境条件与热状况等其它因素的影响,同时,由居民区、道路、耕地和湖泊等景观形成的热环境斑块相互作用、相互影响,构成了一个由各种子系统相互耦合的复杂系统。大量的研究结果表明尺度问题是城市热岛效应中的一个关键问题,城市热岛效应是一种在不同尺度的时间和空间上呈现出不同规律和特征的现象,具有多尺度、自组织和临界性,只有深入地研究和理解城市热环境中的尺度问题,才能认识组成因素在不同尺度上的相互作用和城市热岛效应的形成机制[1-7]。
“尺度效应”和“尺度转换”是尺度研究中的两个基本问题,也是当前空间格局与过程变化研究的热点问题和难题,虽然围绕它开展了大量的研究工作,但是突破性的成果并不多,大部分工作集中在景观格局空间异质性的定量描述上。空间异质性是某种变量在空间分布上的不均匀性及复杂程度的定量描述,是自然景观、地表参数的固有性质,是不同尺度间转换的基础和当前尺度研究中的重要内容。研究人员围绕热环境空间格局的异质性,尤其是与之有关的尺度特征,开展了大量研究,郭冠华等[8]以珠三角城市为例,研究了粒度变化对城市热岛空间格局分析的影响,发现30—150m可以作为城市热岛格局特征的分析粒度。孟丹等[9]通过半变异函数分析地表温度的空间异质性,在此基础上,计算不同粒度下的景观格局指数,分析热力景观格局及其尺度效应。韩贵锋等[10]以重庆市主城区为例,探讨了地表温度同归一化植被指数在不同尺度上的相关性,发现在120m尺度上两者之间的相关性最强,并且这种相关性在空间上呈现出较强的异质性。刘宇鹏等[11]使用一种基于区域统计数据的滑动窗口来提取热岛信息,以长沙市为例,分别在6种尺度上进行了试验,结果认为大小为11×11的窗口提取的热岛区域最符合实际。骆杨等[12]以杭州为例,利用2006年2月—2007年2月逐时气象数据,结合morlet小波变换方法分析了杭州热岛周期变化特征,发现在频域上存在多尺度的周期震荡,并且不同尺度上的影响因素也不同。叶露萍等[13]以武汉市为例,采用分形理论构建半径维数,定量描述了从热岛效应中心向四周低温辐射过程中土地利用空间格局的变化特征,发现半径维数能够有效区分各种土地利用在空间结构上对热环境效应的作用效果。高力浩等[14]应用多分形去趋势涨落分析(MF-DFA)方法,研究了中国地区相对湿度和温度序列的多分形特征差异,发现奇异谱3个特征参数的组合能够完整地刻画特定的长程相关特性,相对湿度和温度序列多分形特征的不同能够揭示其生成动力过程的差异。经研究发现,已有的热环境空间格局空间异质性研究成果存在以下不足:(1)采用景观生态学的理论和方法分析热环境的空间异质性,这种分析局限于尺度的离散性以及图像的分辨率,未能完整地描述景观格局中的自相似性特征;(2)采用地统计方法对研究区域的条带数据进行异质性研究,以变程作为分析尺度,未能充分地使用数据及完整地表达尺度特征;(3)采用单分形的方法进行研究,不具备奇异性的定位功能,凭借一个参数不能够充分挖掘景观格局的非线性特征。成秋明通过大量的地球物理和化学场分析研究以后,认为自然界中绝大多数的物理和化学场是服从多重分形规律的,可以使用多重分形模拟景观格局来认识和研究其物理过程中的多尺度特征[15-18]。多重分形是相对于单分形而提出的,单分形是通过一个分形维数来描述,而多分形是通过多个、无穷多个分维数,即用一个形状如钟形曲线的多重分形谱来描述。Agterberg、文战久、胡守庚等分别使用多重分形方法对地球化学、地球物理、地价等自然和社会经济场进行了模拟研究,很好地描述了场结构中的自相似性和奇异性,这对地壳元素和土地价格等在空间上的分布规律认识具有一定的参考价值[19-21]。

图1 郑州市区示意图Fig.1 Urban District of Zhengzhou City
陈云浩等[22]最先引入热力景观的概念,通过景观生态学的理论方法进行热环境的空间格局研究,如前所述,城市热环境的空间格局是各种大大小小、互相嵌套的自然现象及过程作用后的结果,是一个具有自相似性和非线性等特征的动力系统,在空间格局上表现为人为划分下不同级别的热岛斑块,而斑块与斑块之间是由无数个不规则的纹理连接而成,那么从纹理结构研究的角度,借助于多重分形的理论与方法来定量描述热环境的空间格局就构成了本文的出发点。本研究将以河南省省会郑州市为例,除了对热环境空间格局时空变化的异质性进行定量描述以外,还试图对其参数进行物理意义上的解释,为完善热环境空间格局尺度研究理论、热场中的信息识别及提取以及热场插值等提供参考和依据。
1 研究区概况
郑州市位于河南省中部,是陇海铁路和京广铁路的交点,下辖6个市辖区、5个县级市和1个县,面积7446.2km2,人口903.1万。郑州市属北温带大陆性季风气候,冷暖适中、四季分明,冬季最长,历时137d,夏季次之,历时110d,春季较短,仅有55d,年平均降雨量640.9mm,无霜期220d,全年日照时间约2400h。本次研究范围为郑州市的中心城区,范围取自郑州市城市总体规划(2010—2020),由于上街区离中心城区较远,不包括在本次研究中(图1)。随着中部崛起战略和中原经济区战略的全面实施,郑州市以前所未有的城镇化速度进行扩展,土地利用方式及其热环境景观格局也在时刻发生着剧烈的变化,由此引发了一系列生态环境和社会问题。根据中央气象台的高温统计数据,1951—2009年,郑州总高温日合计1015d,在全国省会城市中列第10位,另外据最新统计数据,郑州市的高温指数排名全国第12位,超越了传统四大火炉城市南京市,位居北方省会城市前3位。因此,针对郑州市热环境景观格局时空演变特征进行研究对于认识热岛形成机制、以及缓解城市热岛效应具有重要意义。
2 数据来源与研究方法
2.1 研究数据
本研究所用数据为1988-05-14、2000-06-16和2011-06-15获取得日期相近的三期TM数据,轨道号为126/36。在处理过程中,采用WGS84坐标系、UTM投影,投影带号为49°N。以2011年影像为基准图像,对另外两期图像分别进行精校正,分辨率统一采样为30m,在图面上均匀选择50个左右的控制点进行验证,最大控制误差不大于半个像元。经裁剪后的郑州市遥感数据清晰度高、无云层覆盖,适合用于本次研究,研究过程在ENVI和MATLAB软件中来实现。
2.2 温度反演
传感器接收到的热辐射遥感信息包括地面发射的热辐射、大气自身向上的热辐射以及大气向下的热辐射经地面反射后被传感器吸收的辐射,主要影响因素有大气效应、地表比辐射率等因素。本研究地面温度反演根据NASA官方的Landsat用户手册提供的算法进行计算。
第一步 计算热辐射能量值
Lλ=gain×DN+bias
(1)
式中,Lλ为由DN值转换后的热辐射能量值(mWcm-2sr-1);DN为像元灰度值;gain和bias分别为TM第六波段的增益和偏移值,可以通过TM的头文件获取。
第二步 计算辐射亮温
(2)
式中,T为传感器辐射亮温;K1和K2为定标参数,K1=607.76 (W m-2ster μm-1);K2为1260.56K。
第三步 计算地面温度
(3)
式中,λ为TM6的中心波长(11.5μm);=h×c/=1.438×10-2mK(斯特藩-波耳兹曼常数=1.38×10-23J/K,普朗克常数h=6.626×10-34Js,光速c=2.998×108m/s);ε为比辐射率,取值于参考文献[23]。
2.3 植被覆盖度
植被热容量相对较大,具有比建筑用地小的辐射能力,潜热存储能力也大于感热,是热环境的重要影响因素。通常来说,利用实验手段直接调查植被信息的工作量和困难程度都比较大,因此一般采用能够反映植被生物量和和长势指示性意义的指数来间接表示。在遥感影像上,通过对不同波段组合能够得到反映植物生长状况的指数,根据所采用波段和计算方法的不同,可以分为多种植被指数,其中NDVI是应用最广泛的一种指数.其计算方法如下[24]:
NDVI=(NIR-R)/(NIR+R)
(4)
式中,NIR为近红外波段,R为红波段。
由于植被指数是间接地获取地面植被的覆盖信息,是一种对植被覆盖的综合、抽象和概化度量,不能直接度量植被覆盖状况,因此,需要将植被指数转化为植被覆盖度。NDVI植被覆盖度的计算公式如下:
f=(NDVI-NDVImin)/(NDVImax-NDVImin)
(5)
式中,NDVImin为裸土或无植被覆盖区域的NDVI值,即无植被像元的NDVI值;而NDVImax则代表完全被覆盖的像元的NDVI值,即纯植被像元的NDVI值。
2.4 多重分形与计算过程
与单分形相比,多重分形理论中最重要的参数是多重分形谱和奇异性指数,前者描述了整个现象的结构,后者反映了分形体中的局部信息,常常被用于热红外目标分割和地球化学场异常圈定中,另外,使用多重分形谱进行比较研究可以有效避免不同时间和不同环境对于热环境场的影响。
2.4.1 多重分形理论
对于具有几何支撑的连续随机空间分布变量,这种支撑可以由通过k维空间Rk(k=1、2、3)分割产生的许多单元(盒子/格子)组成,记每一等分盒子的线度为ε。假设μ(S)表示集合S在Rk中的测度,边长为ε的第i个盒子中的测度为μi(ε)。则μi(ε)与ε的对数比值被限制在一个有限区间[αminαmax],这里存在-≥αmin≤αmax≤,αmin和αmax分别对应最强的奇异性和最弱的奇异性,且有:
(6)
这里的非整数αi称为coarse holder指数。把在分形上具有相同α值的小盒子数目记为Nα(ε),它与ε的大小无关,并且可以写成:
Nα(ε)∝ε-f(α)
(7)
将上式与N(ε)ε-D的简单分形公式对比,可见f(α)的物理意义是表示具有相同α值的子集的分形维数,或者说它描述了ε0+直方图N(ε)的变化,f(α)定义为具有相同α值的子集的Hausdorff维数,称为多重分形谱(Multifractal spectrum)或奇异性谱(Singularity spectrum):
f(α)=dH{xsuppμ,α(x)=α}
(8)
在多重分形谱的众多计算方法当中,矩方法是最常用的方法之一。为了解f(α)的分布特性,定义分割函数(Partition Function):
(9)
(10)
通过勒让德变换(Legendre transformation),通过q和τ(q)可以变为α(q)和f(α):
(11)
反之,知道α(q)和f(α)也可以求出τ(q)和Dq,q-Dq和α-f(α)谱构成了描述多重分形谱的基本数学语言[25]。
2.4.2 计算过程
(1)选择定义在支撑区间里的温度差作为本研究中的测度,即滑动盒子中的温差,假设图像为M×N个像素,使用一组不同尺度ε的正方形盒子对整个图像区域进行覆盖(需要(M/ε)×(N/ε)个),计算每个盒子中的温差Tε=(Tmax-Tmin)/ε,把Tε想象成图像曲面的高度,然后用Tε+1个盒子进行覆盖,就可以用μ(ε)=(Tε+1)/(Tε+1)来求取区域测度[26-27]。
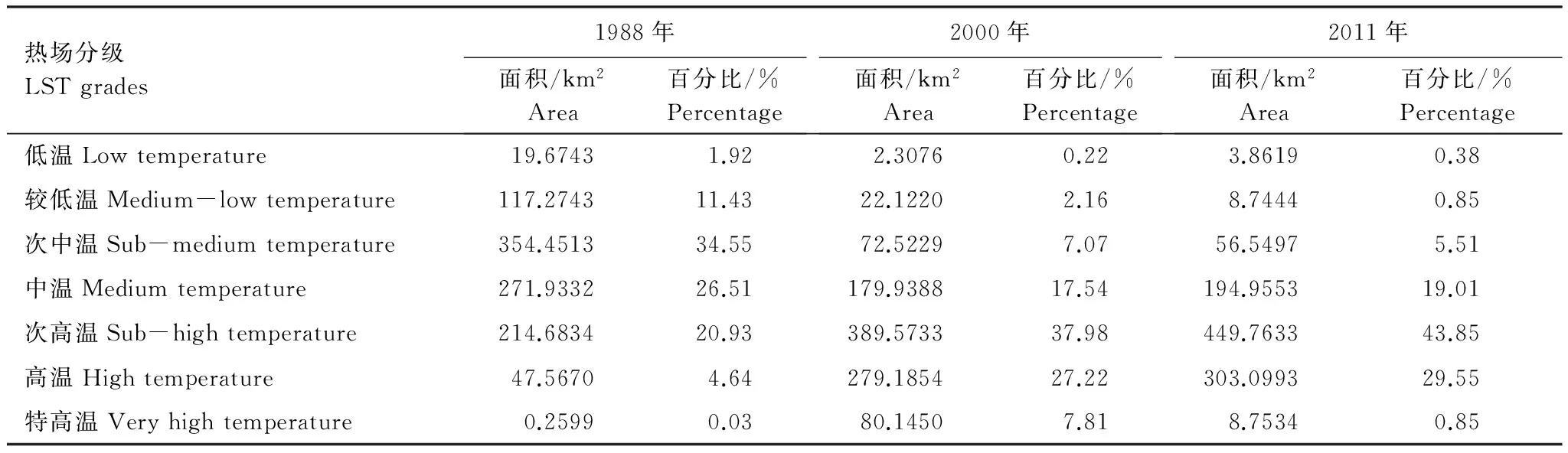
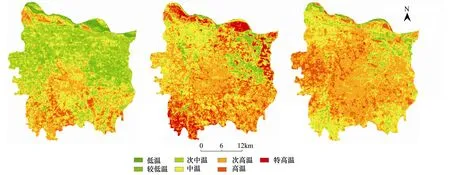
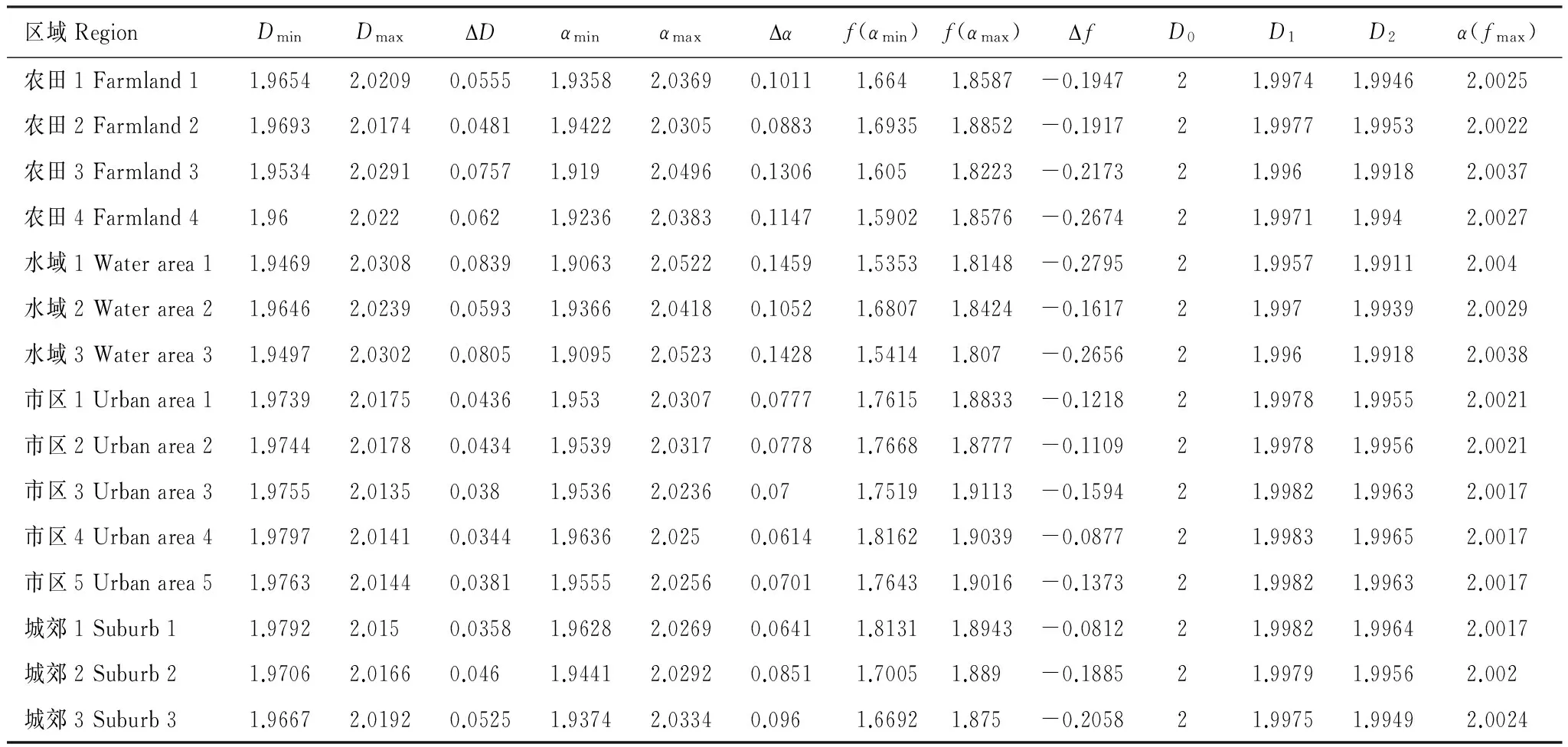
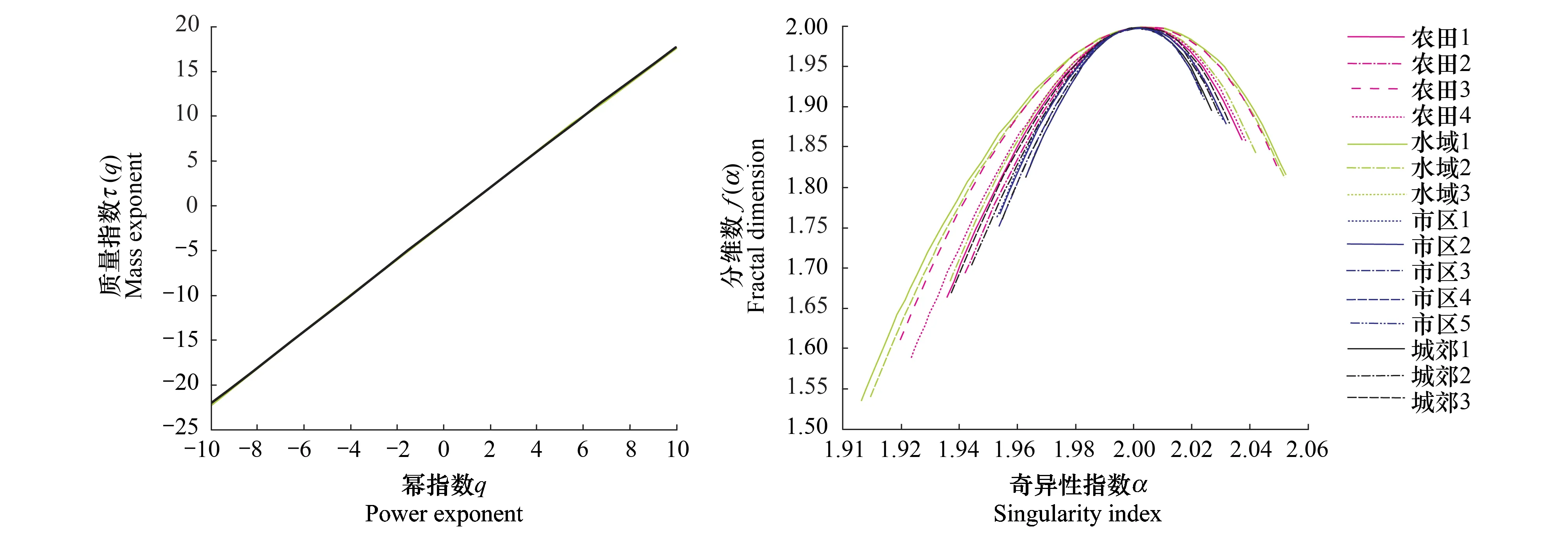
(2)取-10 (3)使用公式α(q)=(τ(q+1)-τ(q-1))/2计算α(q)。 (4)使用公式f(α)=qα(q)-α(q)计算f(α)。 为了对不同时间的热场影像景观格局进行对比分析,本文使用徐涵秋[28]提出的归一化方法将热场影像归一化到0—1区间内,这样有利于消除时间和背景信息的影响,然后按照等间距分级法对热场影像进行分级。鉴于对不同发展区域土地利用类型产生的纹理结构进行定量描述,分级数不应小于相应土地利用类型数目的原则,将热场分为7级,由低到高分别对应低温、较低温、次中温、中温、次高温、高温、特高温,其中次高温到特高温为热岛区域。从表1可以看出,以中温为界,低温到次中温面积显著减少,次中温面积减少幅度最大,净减少29.04%;次高温到特高温面积显著增加,其中高温面积增幅最大,净增24.91%;中温区域的面积呈减少的趋势,减幅为7.5%。另外,通过计算城市热岛比例指数URI,1988—2011年分别为0.36、0.68和0.75,发现20年来郑州市的热场面积显著增加。从三期热场影像的空间分布来看(图2),高温区域主要位于市区及裸露地表,而低温区域主要由植被覆盖区域和水域构成。1988年,特高温区域出现在郑州热电厂、纺织大世界、桐柏北路铁路用地和中原中路边的工业用地等区域。2011年中原区城镇化区域显著扩大,出现了长宏机械制造公司、郑州泰祥热电股份有限公司特高温斑块,除了上述区域,其它能耗大、人口密集区域如北陈伍寨市场、东方雪铁龙河南瑞铭、正道花园百货附近也出现了特高温斑块。总之,1988—2011年间,郑州中心城区的城镇建设用地面积显著增加,因土地利用变化导致的高温区域明显增加,位于城区西部的中原区热场变化明显,尤其是在长椿路和科学大道附近,全市的高温区域主要集聚其周围,其它辖区的次高温面积也出现了大幅度地增加。从热场图像可以看出,位于老城区的热场斑块形状和结构20年间逐渐变得更加复杂,例如,碧沙岗、绿城广场等区域附近出现城市绿岛,这也凸显了旧城改造引起的热场效应变化。 表1 1988—2011年间热场分级面积统计 图2 郑州市热场分级图Fig.2 Grade maps of Zhengzhou thermal field from 1988—2011 多重分形谱函数是城市热环境场格局和结构的直接反映,表现了分维数f(α)随奇异性指数α的变化过程,给出了不同奇异性度量下的分维数,即通过奇异性指数将研究对象分为多个区域并给出每个区域复杂性程度的定量描述。某点的奇异性指数α是该点不同尺度上的测度取对数值后的斜率,计算的时候,依次用不同尺度的盒子对某点进行覆盖来求取,反映了该点自相似性和奇异性的强弱程度,可用于进行空间定位。Dq表示广义分形维数,D0、D1和D2分别代表容量维、信息维和关联维,图3为Dq-q的图形,可以看出,Dq是关于q的单调递减函数,不同的q值对应不同的广义分形维数,Dq偏离D0越大,分形体结构越接近于点状,像元的数目也就越少,结构也就越趋于简单,Dq同f(α)的意义类似。从图3中可以看出,研究区域的三期热场影像均服从多重分形规律,其中也可以利用D1-D0来判断是否服从多重分形规律。根据统计物理学中f(α)和α的解释,αmin代表了概率测度最大的子集,对应于由最大测度像元构成的图案,本文中采用盒子温差作为纹理特征描述算子,因此αmin代表了由最大盒子温差所对应像元构成的纹理区域;相反,αmax代表了由最小盒子温差所对应像元构成的纹理区域,α表示纹理测度分布大小的均匀程度,α越大,概率的分布范围越宽,纹理测度分布越不均匀。一般情况下,热场中盒子温差最大的像元体现了斑块与斑块之间的边界,比如水体、绿地、林地和城建用地或者裸地的边界,盒子温差最小的像元则体现了斑块内部的纹理结构。f(αmin)代表了最大概率测度的分维数,反映了最大概率测度的个数;f(αmax)代表了最小概率测度的分维数,反映了最小概率测度的个数;f(α)max代表了最大的分维数,反映了概率测度最多个数的分维数。f代表了最大测度与最小测度个数的比值,反映了最大温差与最小温差单元个数的比例关系。 图3 1988—2011年三期热场的多重分形谱Fig.3 Mutifractal parameters of Zhengzhou thermal field within a period from 1988 to 2011 为减少位于市区边缘的热异常以及滑动滤波过程中不规则边界产生的影响,选取郑州中心市区1024×1024个像元区域进行计算,本区域基本上涵盖了郑州市的中心城区,能够代表近20年社会经济和城镇化发展的特点。从3个不同年份的多重分形谱f来看,左半部分的表现说明了2000、2011年相同纹理测度值下的分维数比1988年大,像元图案更复杂或者数目更多。产生上述结果的原因是由于城市面积进一步扩大,而城市用地的类型主要是由工业仓储、交通运输、商业与服务业、居住、绿地、水域等组成,纹理结构复杂,热辐射差异表现比农田、水域和城郊等区域大,反映了不同斑块之间混合的均衡程度,因此,可以通过f的左半部分比较不同城区中高温与水域、绿地等低温斑块之间的混合程度,某种程度上可以反映低温斑块的降温效应,混合的越均匀,越有助于降低特高温斑块的面积。α(fmax)为研究区域中概率最大值的像元奇异值,反映了辐射差异的背景信息,通常由大型或优势斑块所决定,可以据此判断基准温度的变化,20年间朝左移动,意味着背景场纹理测度值在增大,整体性温度有升高的趋势。f值总体上是增加的,表明最小值与最大值的个数比例在增大,意味着最小测度纹理边缘在相对增加,它们之间的差异在增大。从三期热场影像的f(α)-α钟型曲线和表2可以看出,1988年和2000年热场图像中的纹理测度取值区间最宽,包含的纹理信息量最丰富,区域纹理高程值波动幅度更大,2011年的结果则相反,究其原因,1988、2000年的城镇化水平较低,农田、郊区等区域面积大于或接近市区面积,导致f的右半部分较宽。信息维D1和关联维D2呈现先减小后增大的趋势,分别在2000年的时候达到最低值,意味着在不同的尺度演绎下2000年的区域辐射差异值最大,即纹理高程值的直方图分布最不均匀,不同强度的热岛斑块表现的更加破碎化且较均匀地相互穿插集聚在一起,反映了郑州市2000年经济处于快速发展时期引起的土地斑块之间的迅速转换。经上述讨论可知,城市的热辐射过程是非线性和自相似的,热场景观格局是不同过程相互作用的结果,不同等级的热岛斑块分别对应着一个或者数个生态过程,而不同过程可以用多重分形中的尺度不变性来表示,这就为热岛信息提取、分类提供了一种新的异于传统正态分布统计量计算阈值的方法,也为城市热场非线性插值、尤其是由其它过程导致的城市热污染、震前热红外异常识别以及地下煤火监测等提供了理论依据。 表2 三期热场影像的多重分形参数统计表 为了研究分布在不同区域上热场空间景观格局的多重分形模式和纹理特征,根据按不同基质和斑块构成的景观格局特征选取的原则,本文在2011年热场图像上选取了15个大小为128×128个区域(图4)进行研究,其中1—4号区域除了农用地基质以外,还含有农村居民点用地、道路交通用地、水域用地等类型斑块;5—7号区域除了水体基质以外,还含有农用地、城建用地等类型斑块;8—12号基质为城市建设用地,还含有水体、绿地等类型斑块;13—15号为城郊区域用地,其中农用地和城建用地的面积接近相等,属于城镇化最为活跃的区域。为了能够清楚地阐述研究问题,根据选择区域中的优势斑块、区域特征以及辐射差异对上述区域进行命名:1—4号而水体分布概率代表农田,5—7号代表水域,8—12号代表市区,13—15号代表城郊。计算结果见表3和图5,从表3中可以得出,水域αmin最小,从小到大依次为农田、城郊和市区;αmax、α的情况恰好与αmin相反,从大到小依次为水域、农田、城郊和城市区域;市区的f(αmin)、f(αmax)、f、D1和D2值最大,其余由大到小依次为城郊、农田和水域,而α(fmax)值则恰好相反。从α值的表现来看,水域具有最大的纹理测度最大值和最小的纹理测度最小值,市区具有最小纹理测度最大值和最大的纹理测度最小值,农田、城郊则介于两者之间;水域具有最宽的纹理测度取值范围,即纹理信息含量最大,说明α值与分析尺度上的辐射差异紧密相关,反映了低温与高温斑块间的边缘测度信息,水体含有更多更强的大型纹理信息,而市区则包含的是小型纹理。f(α)的分布规律表明市区的纹理测度最大值和最小值的分布概率最高,即像元数量最多,并且它们之间的数量差异最小;水体分布概率最小,它们之间的数量差异最大,反映了市区纹理强度分布比较均匀。相对于α,D1则代表了纹理测度值像元数量分布的均匀程度,D1越大,直方图包络曲线就越陡,反之则越缓,从表中可以得出市区的纹理测度像元数量分布最均匀,而水域则分布最不均匀,f(αmin)、f(αmax)和f值也验证了这一点。D2是关联维数,可以用分布在原子核周围的电子云概率密度来解释它的物理含义,D2越大,表明电子在原子核周围出现的概率分布越不均匀,即簇聚程度越高;相反,D2越小,表明电子出现的概率均匀地分布在原子空间内,簇聚程度越低。进一步研究其在热场图像中的含义,首先假设归一化后的热场纹理测度视为原子核周围的电子云密度,那么某个盒子中的纹理测度越高,意味着相对应的电子云密度就越大,因此D2在某种程度上反映了纹理测度在空间上分布的均匀程度,反映了空间中纹理测度值的密度差异,从表中可以得出市区的纹理测度簇聚程度最高,即空间分布最不均匀,而水域则簇聚程度最低,即空间分布最均匀。α(fmax)值从市区到水域逐渐增大,意味着分形谱曲线右移,表明背景场纹理测度值是逐渐降低的。从市区的不同城镇化率区域分析来看,农田、水域的多重分形参数值与市区、城郊之间的差异较大,表明随着城镇化区域的扩大,这种由多重分形过程引起的自相似特征有趋同的趋势。 图4 不同斑块组合样区分布图Fig.4 Distribution of sample area composed of various patches 表3 不同样区多重分形参数统计表 图5 2011年不同区域热场的多重分形参数Fig.5 Mutifractal parameters of different areas distributed throughout Zhengzhou City in 2011 在农田样本中,中心区域为丘陵地形,且含有尖岗水库、孔河等景观的农田3具有最小的αmin值,紧随其后的是耕地面积最大且含有河南豫棉物流有限公司、中国石油物资郑州公司等大型硬质斑块的农田4,农田1和2则为典型的农村宅基地用地、耕地以及零星的道路、工业用地等类型构成的区域。在市区样本中,市区2的α值比市区3大的原因是市区3中分布着碧沙岗公园、月季公园以及绿城广场等低温斑块,而D2值小的原因是市区3位于市中心,属于老城区,斑块破碎化程度高,密度大,而市区2毗邻城郊,属于新开发区域,规划较好;从市区的多重分形参数来看,新开发的区域比老市区具有更小的αmin值和D2值。在城郊样本中,城郊1的城镇化率最高,且没有任何水体,拥有老鸦陈村、普罗旺世等大型硬质地表斑块,也含有河南省体育中心及郑州大学体育学院等综合服务设施用地,城郊3含有郑州植物园、常庄水库等低温斑块,导致城郊1的αmin值最大,城郊3最小。 由于多重分形参数反映了区域的纹理结构特征,而某个区域的温度又受到其结构特征的影响,那么它们之间究竟存在什么样的相关关系呢,为了定量分析这个问题,本研究对15个区域的温度数据统计量分别与多重分形参数进行线性回归,回归结果见图6与图7。从图6与图7中可以得出,区域温度均值与Dmin、αmin、f(αmin)、f(αmax)、f(αmin)-f(αmax)、D1、D2呈显著的正相关关系,即随着水域、农田、城郊和市区多重分形参数的逐渐增大,区域温度也在不断增大;而与Dmax、D、αmax、α、α(fmax)呈负相关关系,即随着水域、农田、城郊和市区多重分形参数的不断增大,区域温度在不断减小。另外,区域温度标准差与多重分形参数之间同样存在着显著的线性关系,且拟合程度比区域温度均值更好,从图7可以看出其与Dmin、αmin、f(αmin)、f(αmax)、f(αmin)-f(αmax)、D1、D2负相关,即从水域农田城郊市区,区域方差是不断减小的;而与Dmax、D、αmax、α、α(fmax)呈正相关关系,即从水域农田城郊市区,区域方差是不断增大的。通过上述实验结果可以得出以下启发:具有较小αmin,较大αmax和α值的水域、农田呈现出较低的温度,意味着可以通过改变地表材料的物理性质,提高诸如水体、城市绿地、土壤等高比热容下垫面的覆盖率以增加纹理测度最大值、热辐射差异和区域的冷岛效应,最终实现降温;不同测度值的分维数f代表了斑块的周长、面积以及边缘纹理信息的复杂性,因此从不同区域分形谱的形态来看,可以通过提高冷岛斑块的面积、周长以及分维数来实现降温;另外,水体、农田区域的信息维和关联维小于城郊和市区,那么究竟通过降低信息维和关联维的措施能够实现降低温度吗?通过分析可知,这个结论对于由相同类型的低温、高温斑块以不同的配置方式构成的区域来说是成立的,反之,对于不同斑块类型不同配置方式构成的区域来说,结论不一定成立。鉴于标准差与研究区域之间存在良好的线性关系,可以将这种关系由斑块组合区域演绎到单一斑块区域中,进一步探讨单一土地利用类型斑块的多重分形特征。 图6 温度均值与多重分形参数之间的关系Fig.6 Relation between average temperature defined on boxes and multifractal parameters 图7 温度标准差与多重分形参数之间的关系Fig.7 Relation between standard deviation of temperature defined on boxes and multifractal parameters α值是奇异性指数,反映了热场局部的结构特征,其值偏离轴线越远,代表奇异性就越强,可以通过α值的大小将热场图像划分成不同的尺度区间,每个区间具有标度不变性,即自相似性。采样尺度选取5×5的像元来进行计算,由于是按照纹理结构进行分类的,因此每个计算单元中包含了多个不同组分的像元,由于像元分辨率的限制,很难获取代表单个地物的纯净像元,通常看到地都是由不同组分组成的混合像元,从这种角度来看,那么这种划分过程也是科学的,这种演绎过程也类似于尺度转换过程中升尺度推演过程(Upscaling)。本研究按照由Cheng[29]提出的C-A方法来进行分割,C-A是一种利用测度同面积之间的幂律关系而提出的一种滤波方法,它可以有效地区别不同标度区间的信息,按照谢淑云[30]提出的划分方法将城市热场划分为三类,分割阈值分别为1.4、1.6、2.0,通过研究发现,小于1.4的区域包含了绝大多数市区内部的纹理结构,1.4—1.6区域则近似代表了郊区农田的纹理结构,2.0以上区域则近似反映了不同斑块之间的边缘信息,即小于2.0的区域可以近似看为斑块内部纹理信息,而大于2.0的区域视为斑块边缘纹理信息。接着计算每个单元中的LST均值和NDVI均值,并将热场中的水体剔除,回归结果见图8。一次性系数反映了地表温度对于植被指数的敏感性,从图8可以看出,一次性系数的绝对值随着区域温差的增大而增大,说明斑块的边缘区域,地表温度对植被指数反应敏感。回归函数的常数项基本上体现了不同α值上LST的基本大小,发现随着α值的增大,常数项是增大的,即α值的贡献是正向的。 图8 不同的α值对NDVI与LST之间关系的影响Fig.8 Effects on LST from NDVI caused from different singularity index α 20年间郑州市的土地利用变化及其热岛效应均发生了剧烈的变化,热环境场的动态调查对于合理进行城市规划和舒缓城市热岛效应具有重要意义。本文借助于多重分形理论定量地描述了郑州市热环境场纹理结构在时间和空间的演变特征,与普通分形的单参数相比,多分形提供的多个参数均表现出较好的规律性,有助于人们从多个角度描述和研究城市的热环境特征。研究结果表明:20年间由于地表下垫面结构的变化,郑州市热环境场的多重分形谱变窄,1988、2000年两期热场的纹理测度大小分布均匀程度最低,纹理测度(盒子温差)背景值有升高的趋势;以水体为基质的盒子温差最大值最大,纹理测度大小分布均匀程度最低,中心城区的盒子温差最大值最小,纹理测度大小分布均匀程度最高;区域温度统计量与水体、农田、市区和城郊等区域的多重分形参数之间呈现出良好的线性关系,其中区域温度标准差拟合程度最好。 不同于其它以温度作为统计量和对象的研究,本文以格子单元中的温差作为统计量,即纹理测度,对城市热场纹理结构进行了分析,刘艳红[31]指出盒子中的温差,即某区域温差,可以反映该区域内部的降温潜力,反映斑块的边缘和异质性,α值越大,表示盒子中的异质性越强,降温潜力越大,位于轴线两侧的盒子,则表明异质性越小,降温潜力越小,究竟哪种结构有利于降温以及降温作用是由水体还是绿地引起等一系列问题还需要进一步探索和研究。从文中选择的15个研究样本来看,αmin与αmax有着一致的变化趋势,根据分析研究,αmax受到边缘引起的伪α极值的影响较大,其变化规律还需进一步研究。在分区研究中,不同的区域反映了斑块类型之间的组合和结构信息,对应着不同的多重分形参数和不同的温度,由于研究区域不同,不能得出较小α值具有较小温度的结论,如果研究区域一致且斑块类型相同,那么其结果更具有说服力。多重分形是一种捕捉奇异性的有效工具,属于幂律分布,不同于主要描述均值附近的正态分布,因此,极易受到一些极值,比如一些强热力像元,诸如电厂、热加工车间和热污染区域等奇异性强的像元的影响,从而导致多重分形谱产生变化。D2表示了空间中质点的簇聚程度,即分布均匀性,从水体到市区逐渐增大,结合其计算公式,发现其反映了较大值的信息,也就是说有极大值的区域其斜率坡度较缓,而极大值较小的区域则坡度较陡,因此也就不难解释含有水体区域拥有较大D2值的原因。 另外,由于遥感数据的获取时间是某一个瞬时时间点,三期影像很难精确调整到同一时刻,同物异谱和异物同谱的现象大量存在,例如2000年遥感图像中小麦收割后的农用地和其它两期存在显著的光谱特征差异,导致热场景观结构的复杂性和不确定性增加,也增加了解释的难度,因此使用某一刻热场影像的纹理特征并不能完全代表一整年的纹理特征,其具有时间上的局限性。由于实际的计算方法与模型的理论推导过程很难做到完全一致,比如,测度的选取、盒子的设置(各向同性和各向异性)等,且所有的计算公式均是在尺度趋于无穷小的条件下得来的,数据分辨率很难满足这一点,导致计算结果存在偏差。另外,由于提取测度或者计算分形参数过程中的滑动平均滤波行为会产生边缘效应,αmax、αmin的计算结果往往还混入了一些伪边缘信息,因此其并不能完全代表热场中的极值像元,因此在解释对应的实际情况时,需要特别注意。总之,从分析过程及分析结果来看,本文可以作为城市热场空间异质性研究的一次有意义的探索,下一步将采用如MODIS等低分辨率的数据,或者其它尺度转换方法,例如利用温度与NDVI之间的关系进行降尺度插值等方法进行分析研究,为进一步丰富和完善多重分形在城市热场空间异质性中的研究理论提供依据。 [1] 张佳华, 孟倩文, 李欣, Yang L M. 北京城区城市热岛的多时空尺度变化. 地理科学, 2011, 31(11): 1349-1354. [2] 张健, 章新平, 王晓云, 张剑明, 刘燚, 肖艳. 北京地区气温多尺度分析和热岛效应. 干旱区地理, 2010, 33(1): 51-58. [3] 程兴宏, 徐祥德, 张胜军, 丁国安. 北京地区热岛非均匀分布特征的卫星遥感——地面观测综合变分分析. 气候与环境研究, 2007, 12(5): 683-692. [4] 江学顶, 夏北成, 郭泺, 李楠. 广州城市热岛空间分布及时域-频域多尺度变化特征. 应用生态学报, 2008, 18(1): 133-139. [5] Gedzelman S D, Austin S, Cermak R, Stefano N, Partridge S, Quesenberry S, Robinson D A. Mesoscale aspects of the urban heat island around New York City. Theoretical and Applied Climatology, 2003, 75(1/2): 29-42. [6] Atkinson P M, Curran P J. Choose an appropriate spatial resolution for remotes sensing investigations. Photogrammetric Engineering and Remote Sensing, 1997, 63(12): 1345-1351. [7] Becker F, Li Z L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sensing Review, 1995, 12(3/4): 225-253. [8] 郭冠华, 陈颖彪, 魏建兵, 吴志峰, 容晓臻. 粒度变化对城市热岛空间格局分析的影响. 生态学报, 2012, 32(12): 3764-3772. [9] 孟丹, 李小娟, 龚辉力, 赵文吉. 北京地区热力景观格局及典型城市景观的热环境效应. 生态学报, 2010, 30(13): 3491-3500. [10] 韩贵锋, 梁保平. 地表温度与植被指数相关性的空间尺度特征——以重庆市为例. 中国园林, 2011, (1): 68-72. [11] 刘宇鹏, 杨波, 陈崇. U-TAE算法提取城市热岛信息的空间尺度分析. 地理科学进展, 2011, 30(9): 1118-1124. [12] 骆杨, 周锁铨, 孙善磊, 薛根元, 顾人颖, 黄珏. 杭州城市热岛空间分布及时域-频域多尺度变化特征. 生态环境学报, 2009, 18(6): 2200-2205. [13] 叶露萍, 吴浩, 李岩, 赵晓军, 张佳伟, 尤南山, 崔巍, 黄解军. 分形理论支持下的城市土地利用热环境效应研究——以武汉市为例. 华中师范大学学报: 自然科学版, 2013, 47(4): 578-582. [14] 高力浩, 付遵涛. 中国地区相对湿度与温度多分形特征对比分析. 北京大学学报: 自然科学版, 2012, 48(3): 399-404. [15] 成秋明, 张生元, 左仁广, 陈志军, 谢淑云, 夏庆霖, 徐德义, 姚凌青. 多重分形滤波方法和地球化学信息提取技术研究与进展. 地学前缘, 2009, 16(2): 185-198. [16] 成秋明. 成矿过程奇异性与矿产预测定量化的新理论与新方法. 地学前缘, 2007, 14(5): 42-52. [17] 成秋明. 多维分形理论和地球化学元素分布规律. 地球科学——中国地质大学学报, 2000, 25(3): 311-318. [18] 成秋明. 成矿过程奇异性与矿床多重分形分布. 矿物岩石地球化学通报, 2008, 27(3): 298-305. [19] Agterber F P. 地球化学图纹理的多重分形模拟. 地球科学——中国地质大学学报, 2001, 26(2): 142-151. [20] 胡守庚, 成秋明. 基于多重分形的城市地价场构建方法研究. 中国土地科学, 2012, 26(1): 38-44. [21] 文战久, 刘洪臣, 高星. 地球物理和地球化学异常的多重分形分析与分解. 地球物理学进展, 2007, 22(3): 972-978. [22] 陈云浩, 李晓兵, 史培军, 何春阳. 上海城市热环境的空间格局分析. 地理科学, 2002, 22(3): 317-322. [23] 李金香, 塔西甫拉提特依拜, 雷磊, 田源. 干旱区典型绿洲热场分布规律研究——以渭干河-库车河三角洲绿洲为例. 中国沙漠, 2011, 31(4): 992-1000. [24] 李苗苗, 吴炳方, 颜长珍, 周为峰. 密云水库上游植被覆盖度的遥感估算. 资源科学, 2004, 26(4): 153-159. [25] 陈志军. 多重分形局部奇异性分析方法及其在矿产资源信息提取中的应用[D]. 北京: 中国地质大学, 2007. [26] 杜华强, 赵宪文, 范文义. 北京地区温度场分布与地面空间结构关系的分形描述. 遥感学报, 2005, 9(6): 696-707. [27] Parrinello T, Vaughan R A. Multifractal analysis and feature extraction in satellite imagery. International Journal of Remote Sensing, 2002, 23(9): 1799-1825. [28] 徐涵秋. 基于城市地表参数变化的城市热岛效应分析. 生态学报, 2011, 31(14): 3890-3901. [29] Cheng Q M, Agterberg F P, Ballantyne S B. The separation of geochemical anomalies from background by fractal methods. Journal of Geochemical Exploration, 1994, 51(2): 109-130. [30] 谢淑云, 鲍征宇. 地球化学场的连续多重分形模式. 地球化学, 2002, 31(2): 191-200. [31] 刘艳红, 郭晋平. 基于植被指数的太原市绿地景观格局及其热环境效应. 地理科学进展, 2009, 28(5): 798-804. Spatio-temporal changes of thermal landscape pattern based on a multifractal model: a case study of Zhengzhou City GAO Xin1,*, WU Guoxi1, DU Genyuan2, LI Changpo1,SHEN Huaifei1 1CollegeofUrban-ruralPlanningandlandscapearchitecture,XuchangUniversity,Xuchang461000,China2SchoolofInternationalEducation,XuchangUniversity,Xuchang461000,China Multifractal analysis has been more commonly used than fractal analysis to give a more precise characterization and a multi-scale analysis of non-linear phenomena. Multifractal analysis can also be used to analyze processes having a greater number of parameters. The objective of this study was to use a multifractal model to quantitatively describe the texture structure, spatio-temporal features, and relationship between regional temperature and Normalized Difference Vegetation Index (NDVI) at different invariant intervals for the urban thermal environment field in the Zhengzhou metropolitan area. We used Landsat TM images for three different periods. The results were calculated for the entire area as follows: (1) the difference between the maximum valueαmaxand minimum value of the singularity indexαmindecreased from 0.6716 to 0.6419; (2)αmaxandαminof the singularity index decreased from 1.4644 and 2.136 to 1.4304 and 2.0723, respectively; (3) the singularity value of the backgroundα(fmax) decreased from 2.0111 to 2.0083; and (4) the fractal dimension of the maximum and minimum valuef(αmin),f(αmax) increased from 0.2354 and 1.4877 to 0.3412 and 1.734, respectively. These results show that with the economic development and progression of urbanization in the past 20 years, the information contained in the texture of the thermal field in the Zhengzhou metropolitan area constantly decreased, and its structure and maximum and minimum texture values became simpler and larger, respectively. For selected locations, we observed that urban areas have fluctuated on a small scale with respect to the amplitude of texture, and the largest fractal dimensions of the maximum and minimum values of texture are well distributed at different scales with high clustering properties. Contrasting results were observed for water areas. Furthermore, there were smallerαminandD2values for older urban districts than those reported for newly developed areas. The relationship between the multifractal parameters and regional temperature statistics were clearly linear, with a stronger mean value than the standard deviation, and the order of variation was as follows: water areas, agricultural land, suburbs, and urban area. In addition, the singularity index of the influence of the relationship between regional temperature and the NDVI was evaluated by obtaining a three scale-invariant segmentation field using a concentration-area model based on a 2011 image. The results showed that the regional average value of land surface temperature (LST), composed of patches of edge pixels, is sensitive to the singularity index, and the contribution of the singularity index to the background value is positive, which can provide some guidance for the scaling transformation of thermal images. multifractal; thermal environment field; landscape pattern; texture; concentration-area model 国家自然科学基金联合基金项目(U1304403);国家自然科学基金青年基金项目(41301405);河南省科技攻关(重点项目)计划(132102210398);河南省基础与前沿技术研究计划(132300410349) 2014-05-29; < class="emphasis_bold">网络出版日期: 日期:2015-07-08 10.5846/stxb201405291108 *通讯作者Corresponding author.E-mail: gxin826@126.com 高歆,吴国玺,杜根远,李长坡,申怀飞.面向城市热环境格局时空演变的多重分形模式——以郑州市为例.生态学报,2015,35(20):6774-6787. Gao X, Wu G X, Du G Y, Li C P,Shen H F.A Spatio-temporal changes of thermal landscape pattern based on a multifractal model: a case study of Zhengzhou City.Acta Ecologica Sinica,2015,35(20):6774-6787.3 结果与分析
3.1 城市热环境场演变特征
3.2 城市热环境场的多重分形参数
3.2.1 不同时间热场的多重分形参数


3.2.2 不同热场区域的多重分形参数

3.3 多重分形参数与温度之间的关系
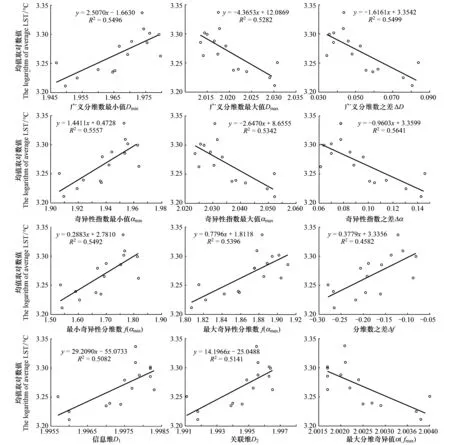
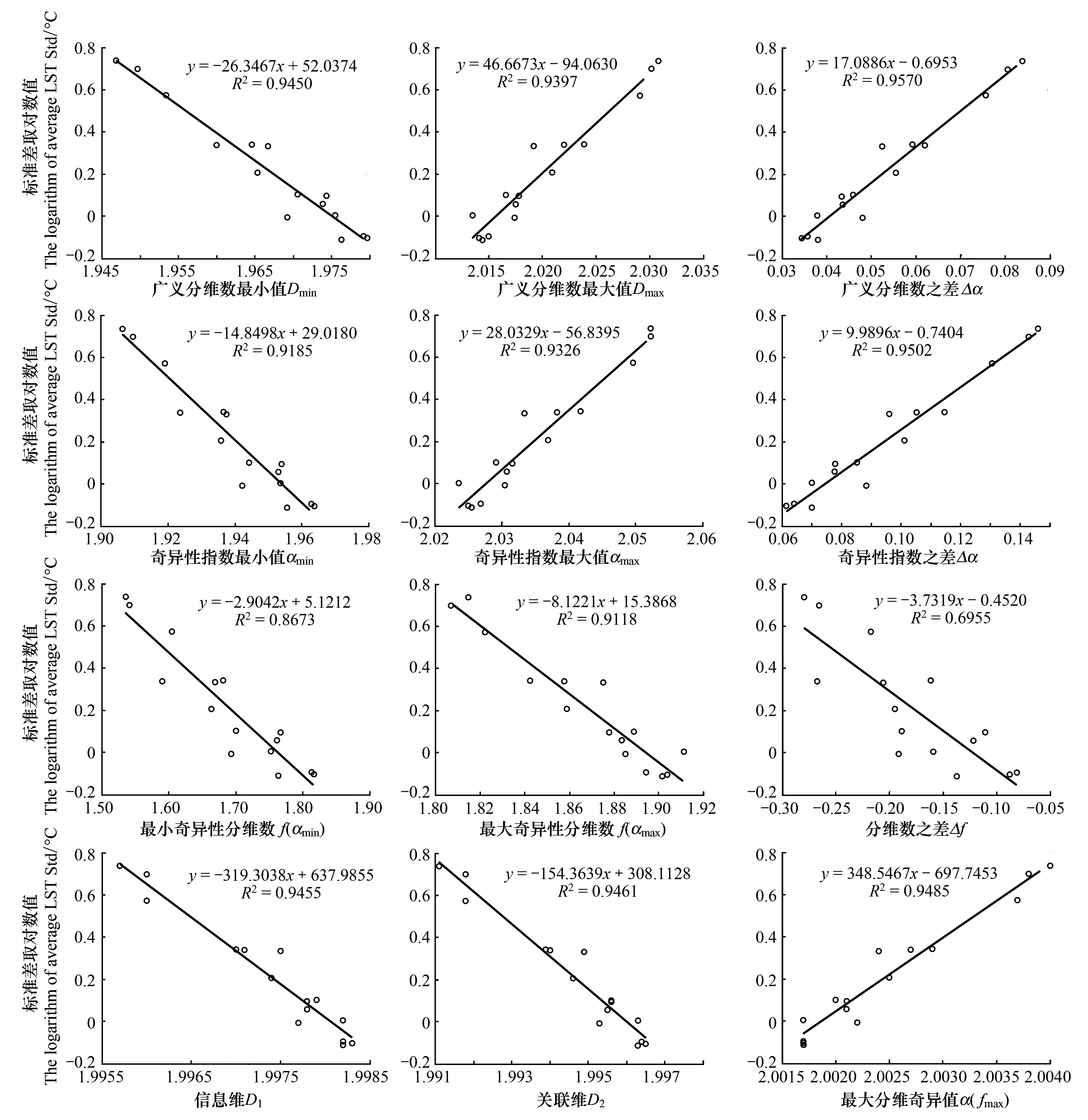
3.4 α对LST与NDVI之间关系的影响

4 结论与讨论
