高桩码头Pushover分析影响因素研究

高树飞，贡金鑫，冯云芬

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.聊城大学 建筑工程学院，山东聊城 252059）

高桩码头Pushover分析影响因素研究

高树飞1，贡金鑫1，冯云芬2

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.聊城大学 建筑工程学院，山东聊城 252059）

非线性静力分析方法或Pushover分析方法是近年提出并在高桩码头抗震设计中得到应用的位移计算方法，该方法将Pushover曲线与反应谱相结合对结构位移进行估计。探讨了影响高桩码头Pushover分析结果的因素，对Pushover分析的能力谱法和N2法及能力谱法中采用的不同等效线性化方法、等效阻尼比公式和不同反应谱进行了定性和定量分析，同时通过一个实际工程案例，比较了上述不同情况的目标位移计算结果。研究表明，能力谱法与N2法的计算结果之间存在差异，差异的大小与能力谱法采用的等效阻尼比计算公式有关；能力谱法中，不同等效阻尼比公式和反应谱曲线下降段的形状对高桩码头目标位移的计算结果有较大影响；Pushover曲线双折线化方法对位移计算结果的影响不是很大。

高桩码头；Pushover分析；目标位移；等效阻尼比；线性化方法；反应谱

高树飞，贡金鑫，冯云芬.高桩码头Pushover分析影响因素研究［J］.水利水运工程学报，2015（5）：1－14.（GAO Shu⁃fei，GONG Jin⁃xin，FENG Yun⁃fen.Influencing factors of Pushover analysis for open typewharfwith standing piles［J］.Hydro⁃Science and Engineering，2015（5）：1－14.）

Pushover分析方法是利用一组单调递增、能近似反映结构地震水平惯性力对结构进行推覆分析结构弹塑性性能的一种方法。推覆过程包括了结构从弹性阶段开始，经历开裂、屈服直至倒塌破坏全过程的信息，因而可以对结构的抗震性能作出评价。但单纯的推覆分析并不能得到结构的地震响应，通常要与反映地震特性的反应谱结合才能对结构的目标位移做出估计。

常用的Pushover分析方法有两种：能力谱法（CSM）和N2法。能力谱法最早由美国学者FREEMAN SA于1975年提出［1］，用于评估海军造船厂房屋的抗震性能，后经改进编入美国应用技术协会报告ACT－40［2］，之后被多本规范采用，成为结构Pushover分析最流行的方法。N2法是斯洛文尼亚FAJFAR P教授最早提出的Pushover分析方法［3－5］，被欧洲规范8［6］采用。对于高桩码头结构，美国《海洋油码头和维护标准》（简称MOTEMS）［7］和《长滩港码头设计标准》（简称POLB）［8］采用了能力谱法，欧洲规范8采用的是N2法。能力谱法和N2法原理不同，即使同一方法不同规范采用等效阻尼比公式和Pushover曲线双折线化方法等也不同，从而计算结果会存在很大差异。另外，采用的反应谱也会影响分析结果。因此，定性和定量了解Pushover分析结果的影响非常重要。本文对上述规范采用的能力谱法和N2法及相关公式的影响进行了定性和定量分析，并通过一个实际的高桩码头工程案例，对计算结果进行了定量分析，目的是为研究高桩码头Pushover分析方法以及为工程人员从事海外工程设计提供参考。

1 Pushover分析方法及误差

Pushover分析方法是基于单自由度体系分析原理的一种地震弹塑性最大反应近似分析法，对于多自由度体系，则需通过第一振型（也可用其他水平力比例）将其转换为单自由度体系。因此，Pushover分析的其中误差之一来自于将弹性第一振型用于弹塑性结构产生的误差，很多文献对此进行了研究［9］。对于梁板式、无梁板式、桁架式和实体墩式高桩码头，可以直接等效为单自由度体系，无需进行转化。因此，这些码头不存在将多自由度体系转换为单自由度体系而产生的误差。

1.1 能力谱法

能力谱法也称为“替代结构法”，即用一个具有“等效刚度”和“等效阻尼比”的“等效弹性结构”代替原来的非线性结构，从而近似采用弹性反应谱理论计算结构的地震反应，其中等效刚度一般采用割线刚度，等效黏滞阻尼比按照非线性结构黏滞阻尼耗能与弹性结构滞回耗能相等的原则确定。众所周知，结构进入非线性状态后，刚度降低，结构的地震反应也会减小；而结构进入非线性状态后的滞回耗能也会降低结构的地震反应。能力谱法则通过增大结构阻尼比、降低弹性反应谱的值来考虑这种非线性地震反应。由于结构的“等效刚度”和“等效阻尼比”都与结构的地震位移反应有关，而位移是需要求解的量，所以采用能力谱法进行分析需要迭代计算。对于高桩码头，文献［7］和［8］均给出了迭代计算的步骤。ACT－40将结构的Pushover曲线转换为能力谱，将反应谱转换为需求谱，可采用图示法表示能力谱法的原理，如图1所示，其中迭代确定的性能点对应的位移为目标位移。

1.2 N2法

图1 能力谱法的性能点Fig.1 Performance point of capacity spectrum method

N2法将非弹性体系等效为弹性体系的出发点是基于这样一个事实：理想弹塑性体系的位移反应与相同周期弹性体系的位移反应有一定关系，即对于中等周期的结构，等效弹性体系的位移反应符合“等能量原理”；对于长周期的结构，等效弹性体系的位移反应符合“等位移原理”。利用N2方法确定目标位移时也需要进行迭代，迭代步骤可见文献［6］。

Pushover分析方法的另一个误差是将弹性体系的结果转化为弹塑性体系产生的。对于单自由度体系而言，能力谱法的误差来自于将弹性反应谱通过改变结构阻尼和刚度近似用于弹塑性结构；N2法采用弹塑性反应谱，而弹塑性反应谱根据弹塑性反应与弹性反应形的近似关系确定。

为比较能力谱法与N2法计算的最大位移的不同，对模型化的单自由度结构进行分析，结构的荷载－变形曲线（Pushover曲线）见图2，第一刚度为K＝1.512× 107N／m，第二刚度系数r＝0.05，结构的质量为m＝T2K／（2π）2，屈服力为Fy＝λmg，其中T为结构周期，λ为相对屈服力（结构屈服力与结构重力之比）。图3给出了λ＝0.1，0.2，0.4，0.6和峰值地面加速度αpg＝0.6g时，采用能力谱法（采用ATC－40的等效阻尼比计算式（式（2））和N2法按欧洲规范反应谱（C类场地）计算的结构最大位移Δd随结构周期（T＝0.1～2.0 s）的变化。

图2 单自由度结构及荷载－变形曲线Fig.2 SDOF and load⁃displacement curve

由图3可以看出，采用N2法计算的位移比采用能力谱法计算位移的大，λ＝0.1时二者之间的差别在自振周期1.0～1.25 s时最大；随着相对屈服力λ的增大，两种方法计算的位移之间的差别越来越小，并随着周期的增大而趋同。

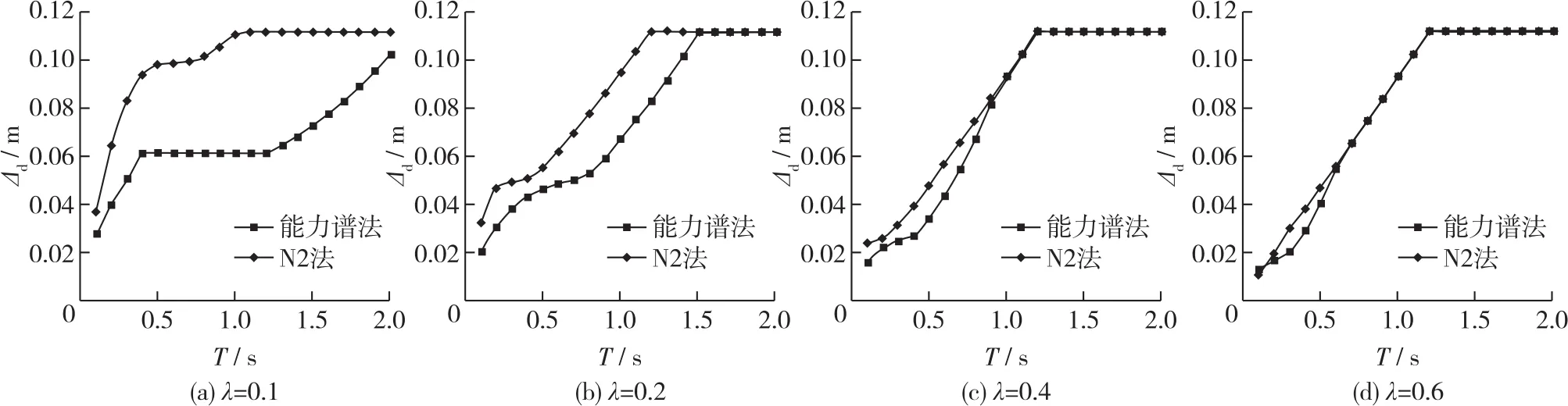
图3 能力谱法与N2法计算的最大位移Fig.3 Maximum displacements calculated by capacity spectrum method and N2 method

2 Pushover曲线双折线化

进行Pushover分析前首先要得到结构的Pushover曲线，Pushover曲线是在考虑结构自重作用的同时，通过对结构施加水平单调递增荷载来将结构推覆至某一预定位移或使结构成为机构所得的荷载－变形曲线。进行推覆计算时，桩土相互作用可采用土弹簧模拟，土弹簧的荷载－位移关系可由p⁃y曲线确定。另外，计算荷载－变形曲线时应力－应变关系中的材料强度采用平均值而不是标准值或设计值［8，10］。

得到Pushover曲线后，还要将其等效为图2（b）所示的双折线力－变形曲线，以获得延性系数μ，屈服后刚度与屈服前刚度比r和割线刚度Ke等参数。不同Pushover方法及不同规范中曲线线性化的方法不同。图4为ATC－40，FEMA 356［11］，POLB和欧洲规范8中N2法采用的双折线化方法示意图。ATC－40的双折线化方法将第一段折线斜率定义为初始刚度Ki，再根据曲线和横坐标轴包围的面积与双折线和横坐标轴包围的面积相等的原则迭代确定屈服点的位置；FEMA 356的双折线化方法首先估计屈服力Fy，第一段折线采用曲线上0.6Fy处的割线刚度，与ATC－40相同，采用面积相等的原则确定屈服点位置；POLB的双折线化方法中，第一段折线刚度采用原点与桩第一个塑性铰形成时连线的斜率，并将实际Pushover曲线在第一个塑性铰形成以前的部分视为直线，再根据面积相等的原则确定屈服点位置，但这样得到的简化折线与坐标横轴包围的面积将小于真实Pushover曲线与坐标横轴包围的面积。MOTEMS采用的方法与POLB相似。N2的分析方法采用理想的弹性－完全塑性体系（图4），初始刚度按实际荷载－位移曲线下的面积与理想荷载－位移曲线下的面积相等确定。理想单自由度体系的屈服位移为

图4 能力谱法和N2法中Pushover曲线的双折线化Fig.4 Bilinear representation of Pushover curves for capacity spectrum method and N2method

由此可以看出，无论是能力谱法还是N2法，确定的Pushover曲线的屈服位移和屈服力均随目标位移Δd的变化而变化。就能力谱法的双折线方法而言，不同规范得到的屈服位移和屈服力也不同。这些都会影响Pushover方法的分析结果。

3 等效阻尼比

等效阻尼比ξeq是能力谱法分析需要采用的参数，是根据非线性体系一个滞回环消耗的能量和与等效线性体系黏滞阻尼消耗的能量相等的原则确定的。根据不同的结构滞回模型，目前已经提出了多个不同的计算公式［12］。式（2），式（3）和式（4）分别为ATC－40，MOTEMS及POLB采用的公式。

式中：μ为延性系数，μ为待求的目标位移Δd与结构屈服位移Δy之比；r为结构屈服后刚度与屈服前刚度之比（图2（b））；κ为修正系数。ATC－40中，根据地震持时和结构新旧程度将结构区分为Type A，Type B和Type C三类，对于不同的结构类型规定了不同的κ值。

在式（2）～（4）中，第1项（即常数项）为结构弹性黏滞阻尼比，第2项为将结构滞回耗能等效为黏滞耗能得到的等效黏滞阻尼比。式（4）根据非线性时程分析结果得出，不根据采用图2（b）所示的双折线骨架曲线的滞回模型提出，因而与r无关。图5为按照上述3个等效阻尼比公式计算得到的阻尼比，对于ATC－40，考虑结构性能类型为Type A。由图5可见，在r较小时，ATC－40的计算结果最大，POLB和MOTEMS的计算结果较接近；在r较大时，ATC－40和POLB的计算结果较接近，但随着μ的增大，二者差别变大，MOTEMS的计算结果较小，在μ较大时甚至出现小于0.05的情况，故在利用MOTEMS的等效阻尼比公式确定Δd时，当阻尼比小于0.05时，应取0.05。3个等效阻尼比模型的较大差别也是引起Pushover分析计算结果出现差异的重要因素。

图5 不同等效阻尼比公式的比较Fig.5 Comparison of various equivalent damping equations

图6给出了λ＝0.1，0.2，0.4，0.6和峰值地面加速度αpg＝0.6 g时，采用能力谱法（等效阻尼比分别按式（2）～（4）计算）按FEMA 356的反应谱（D类场地，SXS＝1.5 g，Sx1＝0.75 g）计算的结构（图2）最大位移Δd随结构周期（T＝0.1～2.0 s）的变化，该图反映了采用的等效阻尼比公式的影响。

由图6可以看出，总体上采用MOTEMS等效阻尼比公式计算的位移最大，POLB次之，ATC－40最小；随着相对屈服力λ增大，采用MOTEMS和ATC－40公式计算的位移随着结构周期增大而趋于相同，因为在屈服力λ较大时，结构的屈服位移较大，在周期较大时，结构的反应为弹性，因而采用MOTEMS和ATC－40的阻尼比公式得到的阻尼比相同，进而计算结果相同，而POLB的等效阻尼比公式的弹性黏滞阻尼比较大（0.1）。

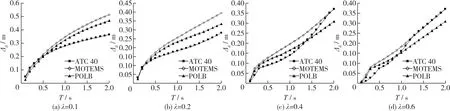
图6 等效阻尼比模型对Pushover分析结果的影响Fig.6 Influence of equivalent damping ratio equation on analysis results

4 反应谱

反应谱是不同周期的单自由度体系对地震的反应。当结构进入非线性状态时，能力谱法通过将结构非线性滞回耗能等效为黏滞阻尼耗能、增大结构阻尼比来考虑结构地震的反应变化，N2法则直接使用非弹性反应谱。图7示出了美国FEMA 356（MOTEMS采用该反应谱）、欧洲规范8和我国《建筑抗震设计规范》（GB 50011—2010）［13］阻尼比为0.05时的弹性反应谱，图中参数的意义可见相关规范或文献［14］。我国《水运工程抗震设计规范》（JTS 146—2012）［15］只给出了5%的阻尼比，不能用于Pushover分析。

图7 规范中的反应谱Fig.7 Response spectra in codes

由图7可见，美国FEMA 356将反应谱分为3段表示，欧洲规范和中国规范分为4段表示，欧洲规范反应谱反映了短周期结构反应加速度与周期的倒数成正比（由速度控制）、中长周期结构反应加速度与周期倒数的平方成正比（由位移控制）的特征。3个反应谱相比，欧洲规范的反应谱最“瘦”，我国规范的“适中”，美国FEMA 356的最“胖”。另外，在美国规范和欧洲规范的反应谱中，平台段的加速度为周期为0时（结构刚度无穷大），加速度为2.5倍，中国规范为2.25倍。结构的地震反应与结构所在场地的类别有关，虽然不同规范场地类别划分的方法、指标和类型数有所不同，但最好一类场地（美国规范和欧洲规范为A类，中国规范为I类）特性比较接近。

将3本规范反应谱坐标的纵坐标统一为相同的表达形式，即加速度反应Sa与地面峰值加速度αpg的比值，图8给出了阻尼比分别取ξ＝5%，10%，20%和30%时3本规范的反应谱曲线。需要说明的是，虽然按欧洲规范进行Pushover分析时不采用调整阻尼比的方法来考虑结构的非线性（而是直接采用非弹性反应谱），这里画出不同阻尼比时的反应谱只是用于比较。由图8可见，随着阻尼比的增大，加速度反应越来越小，但减小的幅度越来越小；FEMA 356反应谱下降最快，GB 50011—2010次之，欧洲规范8最慢。反应谱的区别也会使得采用不同反应谱进行Pushover得到不同的结果。图9给出了λ＝0.1，0.2，0.4，0.6和峰值地面加速度αpg＝0.6g时，采用能力谱法（反应谱分别采用以上3种反应谱，不同反应谱参数确定可参看5.2节；采用ATC－40的等效阻尼比计算式（式（2））计算的结构（图2）最大位移Δd随结构周期（T＝0.1～2.0 s）的变化，该图反映了采用的反应谱影响。

图8 不同阻尼比时的反应谱Fig.8 Response spectra at different damping ratios

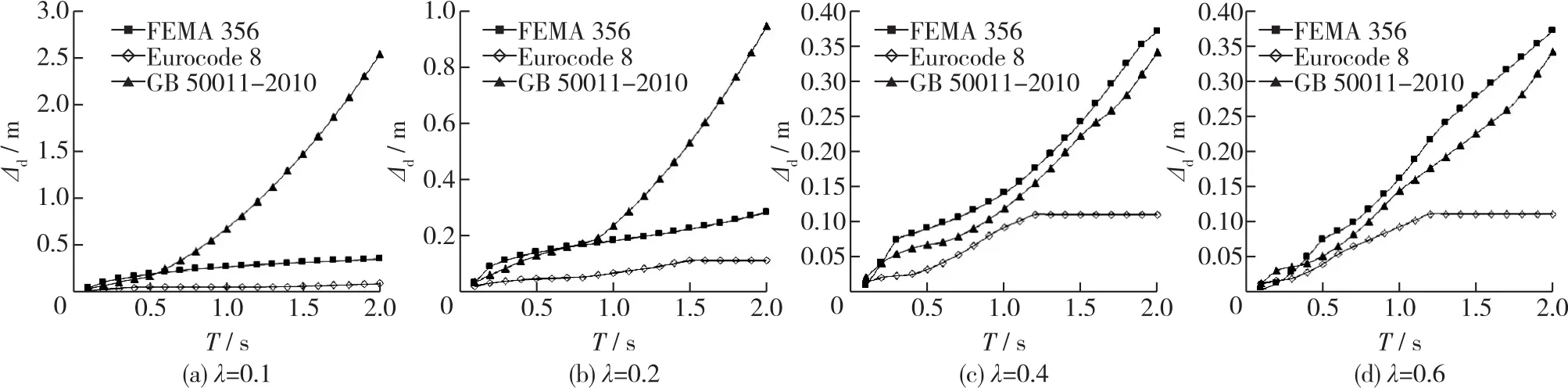
图9 反应谱对Pushover分析结果的影响Fig.9 Influences of response spectra on analysis results

由图9可见，相对屈服力λ为0.1和0.2时，短周期时采用FEMA 356反应谱计算的位移最大，GB 50011—2010次之，欧洲规范8最小。但随着周期的增大，采用GB 50011—2010计算的位移逐渐增大并超过FEMA 356；相对屈服力λ为0.4和0.6时，采用FEMA 356反应谱计算的位移最大，GB 50011—2010次之，欧洲规范8最小。产生以上现象的主要原因是，短周期时FEMA 356反应谱的谱值最大，GB 50011—2010次之，欧洲规范8最小，而长周期时GB 50011—2010反应谱的谱值最大；λ较小时，结构屈服位移较小，等效结构的周期比弹性周期大得多，λ较大时，二者差距相对较小。

5 案例分析

前面从能力谱法与N2法原理、Pushover曲线双线性化、等效阻尼比模型和规范反应谱的不同定性和定量分析了对Pushover分析结果的影响，下面通过一个高桩码头实例进一步定量说明这些因素的影响。

5.1 工程概况

海外某强震区一高桩码头的断面如图10，码头宽28.87 m，排架间距6.3 m，面板厚0.45 m。圆形实心混凝土桩直径0.8 m，横梁高1.9 m，宽1.5 m；前边梁高2.2 m，宽1.5 m；轨道梁高1.9 m，宽1.6m；中纵梁高1.9 m，宽1.5 m；后边梁高1.9 m，宽1.5 m，码头面堆载为40 kPa。当地平均海平面为1.2 m。C，D和F桩与上部结构的连接如图11所示，其他各桩类似。土层标高及物理力学参数列于表1。经判定，按美国规范ASCE 7－05［16］，场地类型为D类，欧洲规范为C类，中国规范为II类。

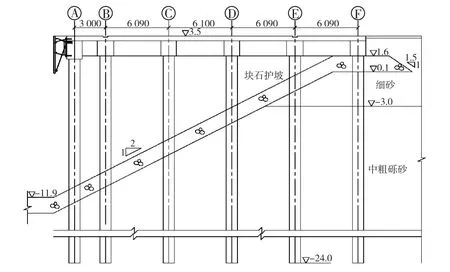
图10 码头断面（单位：高程m，其他mm）Fig.10 Section of wharf（unit：elevation in m，others in mm）

图11 桩与上部结构连接（单位：高程m，其他mm）Fig.11 Pile⁃wharf connection（unit：elevation in m，others in mm）

表1 土体物理力学参数Tab.1 Physical and mechanical parameters of soilmass

5.2 地震动

选取多个地震动水准进行计算，其50年内的超越概率和峰值地面加速度αpg如表2所示。对于中国规范GB 50011—2010，地震分组取为第一组；对于欧洲规范8，选用2型谱。对于中国规范和欧洲规范，直接根据地面峰值加速度和场地类别即可确定反应谱的参数，但对于FEMA 356给出的反应谱，无法确定周期为1 s的谱加速度值SX1，对于本案例中的场地类型，由于欧洲规范8和中国规范GB 50011—2010反应谱中水平段的起始周期均为0.1 s，故本文考虑FEMA 356中T0为0.1 s以确定SX1（如果仅是中美两个反应谱进行比较，通常做法是保证反应谱下降段起点对应的周期相同以确定反应谱参数SX1，由于本文涉及3个反应谱，故近似进行上述处理），并近似按5%的阻尼比确定TS，由此可得各反应谱的参数，结果列于表2。图12为不同规范在某一水准下阻尼比为5%的加速度反应谱。

图12 加速度反应谱（ξ＝5%）Fig.12 Acceleration response spectra（ξ＝5%）

表2 地震动及反应谱参数Tab.2 Ground motion and response spectra parameters

（续表）

5.3 Pushover曲线

由于结构沿纵向对称，取一个排架进行分析。混凝土圆柱体抗压强度采用 f′c＝34.47 MPa，密度为2 400 kg／m3，泊松比为0.167，分析中采用强度平均值f′ce＝1.3f′c。钢筋采用 60级钢，屈服强度 fy＝60 413.7 MPa，屈服强度平均值 fye＝1.1fy，泊松比为0.3，混凝土和钢筋的应力－应变关系根据POLB确定。利用p⁃y曲线考虑桩土相互作用，其中桩在块石中的p⁃y曲线参考文献［17］确定，在细砂和中粗砾砂中的p⁃y曲线按文献［18］确定。Pushover分析模型见图13，分析模型轴线为所有构件截面的中心线，第1个土弹簧设在坡面下15 cm处，坡面下3 m范围内间距30 cm，3 m以下范围内间距60 cm，图中弹簧仅为示意，不代表实际计算中采用的数量和位置。

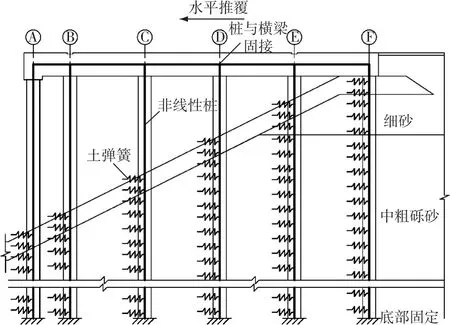
图13 使用p⁃y弹簧的Pushover模型Fig.13 Pushovermodel with p⁃y springs

采用通用有限元软件ABAQUS6.12对码头进行推覆，桩和梁采用二维梁单元B21，梁单元中的钢筋通过∗rebar关键字实现，混凝土采用Concrete Damaged Plasticity模型模拟，钢筋采用 Plastic模型模拟。土弹簧采用Connector单元模拟。在ABAQUS中建立两个分析步，第一个分析步施加重力荷载，参考POLB，重力荷载考虑上部结构自重、面板底部至岸坡以下5倍桩径范围内桩重量的1／3及堆载的10%，结构自重换算为横梁自重，堆载按线荷载施加在梁上；第二个分析步在F桩顶施加水平推覆力（上部结构重心处），逐步增加水平荷载，计算确定水平荷载作用下码头的荷载－变形曲线，在加载过程中发现，桩的首个塑性铰出现在F桩桩顶，对应的位移与荷载见图14。

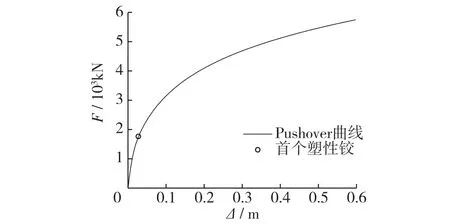
图14 Pushover曲线Fig.14 Pushover curve

5.4 目标位移计算

考虑Pushover分析方法及Pushover曲线双折线化方法、等效阻尼比和反应谱的不同，按以下4种情况对计算的目标位移Δd进行比较。

（1）反应谱相同，Pushover分析方法不同。利用欧洲规范的反应谱，分别采用能力谱法和N2法进行分析，能力谱法中的等效阻尼比分别采用式（2）～（4），Pushover曲线双折线化方法采用ATC－40中的方法，计算结果见图15。

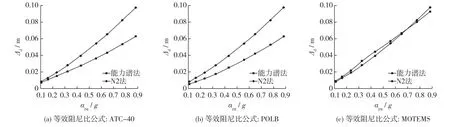
图15 能力谱法和N2法计算的目标位移Fig.15 Target displacement calculated by capacity method and N2 method

由图15可见：①能力谱法中采用MOTEMS的阻尼比公式计算的位移与N2法的最接近，其次是ATC－40；②采用ATC－40和POLB的等效阻尼比公式计算的位移均小于N2法的，采用MOTEMS等效阻尼比公式计算的位移略大于N2法的，但在αpg逐渐增大时有相互接近并小于N2法计算位移的趋势。

（2）反应谱相同，等效阻尼比公式相同，Pushover曲线双折线化方法不同。采用能力谱法计算不同地震水平下的目标位移，计算结果如图16～18所示。图16（a）为采用FEMA 356反应谱及ATC－40中等效阻尼比公式、不同Pushover曲线双折线化方法时计算的目标位移，其他各图的含义类似。

图16 采用FEMA 356反应谱计算的目标位移Fig.16 Target displacement calculated based on spectrum in FEMA 356

图17 采用Eurocode 8反应谱计算的目标位移Fig.17 Target displacement calculated based on spectrum in Eurocode 8

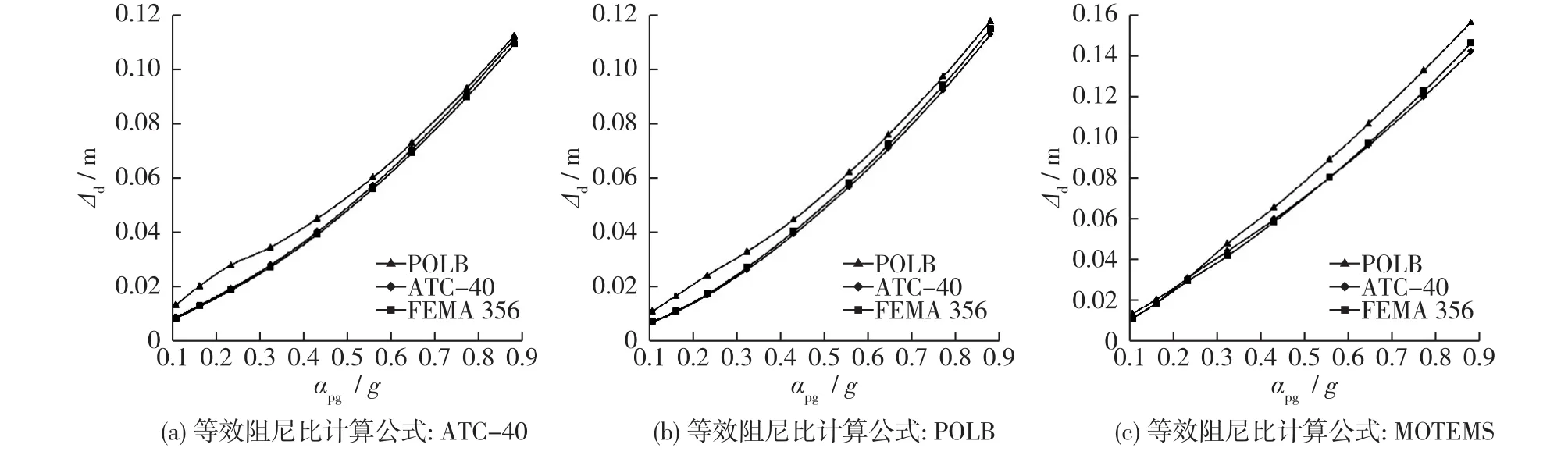
图18 采用GB 50011—2010反应谱计算的目标位移Fig.18 Target displacement calculated based on spectrum in GB 50011—2010

从图16～18可见：①3种Pushover曲线双折线化方法计算的位移差别不大。αpg较小时，采用POLB计算的位移较大，采用ATC－40和FEMA 356计算的位移较为接近，这是因为POLB得到的简化折线与坐标横轴包围的面积小于真实Pushover曲线与坐标横轴包围的面积，这在αpg较小时的影响较为明显，因而等效阻尼耗散的能量较少，反应谱折减较小，进而计算结果较大；②从图16（c）、图17（c）和图18（c）可以看出，αpg较小时，3种方法计算的位移基本相同，这是因为3种方法得到的r均较大，而MOTEMS采用的等效阻尼比公式在r较大时会小于5%。如前所述，在计算过程中出现小于5%时，取5%，故此时等效阻尼比的计算实际上已不受双折线化方法的影响。

（3）反应谱相同，Pushover曲线双折线化方法相同，等效阻尼比计算公式不同。采用能力谱法计算不同地震水平下的目标位移，计算结果如图19～21所示。从图19～21可见：①随着峰值地面加速度αpg的增大，目标位移逐渐增大；②3个等效阻尼比公式中，ATC－40和POLB的计算位移较为接近，MOTEMS的计算位移最大。这一规律与图5中各阻尼比的规律一致，因为目标位移较小时，屈服后刚度与屈服前刚度之比r较大，3个等效阻尼比公式中MOTEMS的阻尼比最小，由图8可知，阻尼比越小，反应谱的折减越小，进而得到的目标位移也相对越大；③从图19可以看出，在αpg超过一定值后，POLB的计算位移大于ATC－40的，这可从图5得到解释，在较小的目标位移范围内，r值较大，ATC－40的阻尼比较POLB小，而随着目标位移的增大，r变小，ATC的阻尼比较POLB大，故目标位移较小。

图19 采用FEMA 356反应谱计算的目标位移Fig.19 Target displacement calculated based on spectrum in FEMA 356

图20 采用Eurocode 8反应谱的目标位移Fig.20 Target displacement calculated based on spectrum in Eurocode 8

图21 采用GB 50011—2010反应谱计算的目标位移Fig.21 Target displacement calculated based on spectrum in GB 50011—2010

（4）等效阻尼比公式相同，Pushover曲线双折线化方法相同，反应谱不同。采用能力谱法计算不同地震水平下的目标位移，计算结果如图22～24所示。可见：①3个反应谱中采用FEMA 356计算的位移最大，GB 50011—2010次之，Eurocode 8最小，规律与图12中各反应谱的规律一致；②αpg很小时，各反应谱结果的相对差别较小，而随着αpg增大，差别越来越大，这是因为αpg较小时，目标位移较小，等效单自由度体系的割线刚度较大，周期较小，而从图12可见，在反应谱下降段以前，3个反应谱间的差别不大。

图22 采用ATC－40等效阻尼比公式计算的目标位移Fig.22 Target displacement calculated based on equivalent damping ratio equation in ATC－40

图24 采用MOTEMS等效阻尼比公式计算的目标位移Fig.24 Target displacement calculated based on equivalent damping ratio equation in MOTEMS

6 结 语

本文对影响目标位移计算的4个主要因素（分析方法、Pushover曲线双折线化方法、等效阻尼比和反应谱）进行了定性和定量分析，并通过案例计算，分析了4个因素对目标位移计算结果的影响。研究得出如下结论：

（1）能力谱法采用MOTEMS阻尼比公式时的目标位移计算结果与N2法最接近，其次是ATC－40；采用ATC－40和POLB的等效阻尼比公式的计算结果均小于N2法。

（2）能力谱法中，采用3种Pushover曲线双折线化方法计算的目标位移较为接近。目标位移值较小时，采用POLB的双折线化方法计算的结果相对较大；相比于等效阻尼比，Pushover曲线双折线化方法对目标位移计算结果的影响较小，基本可以忽略。

（3）能力谱法中，采用不同的等效阻尼比公式对高桩码头目标位移的计算结果有较大影响。采用ATC－40和POLB的阻尼比公式计算的结果较为接近，采用MOTEMS阻尼比公式计算的结果最大。

（4）FEMA 356，Eurocode 8和GB 50011—2010规范反应谱的下降段差别较大，在计算的目标位移上也得到了体现。采用FEMA 356反应谱计算的目标位移最大，GB 50011—2010次之，Eurocode 8最小。

参 考 文 献：

［1］FREEMAN，S A，NICOLETTI JP，TYRRELL J V.Evaluation of existing buildings for seismic risk—A case study of Puget Sound Naval Shipyard Bremerton，Washington［C］∥ Proceedings of the 1st US National Conference on Earthquake Engineering，1975.

［2］ATC－40 Seismic evaluation and retrofit of concrete buildings［S］.

［3］ FAJFAR P，FISCHINGER M.Non⁃linear seismic analysis of RC buildings：implications of a case study［J］.European Earthquake Engineering，1987，1（1）：31⁃43.

［4］FAJFAR P，FISCHINGER M.N2⁃A method for non⁃linear seismic analysis of regular buildings［C］∥Proceedings of the Ninth World Conference in Earthquake Engineering，1988，5：111⁃116.

［5］FAJFAR P，GAŠPERŠIĈP.The N2 method for the seismic damage analysis of RC buildings［J］.Earthquake engineering＆structural dynamics，1996，25（1）：31⁃46.

［6］EN 1998⁃1：2004 Eurocode 8：Design of structures for earthquake resistance—Part1：General rules，seismic actions and rules for buildings［S］.

［7］California State Lands Commission.Marine oil terminal engineering and maintenance standards（MOTEMS）［S］.

［8］Port of Long Beach（2012），wharf design criteria（Version 3.0）［S］.

［9］KRAWINKLER H，SENEVIRATNA G.Pros and cons of a pushover analysis of seismic performance evaluation［J］.Engineering Structures，1998，20（4）：452⁃464.

［10］Permanent International Association for Navigation Congresses.Seismic design guidelines for port structures［S］.

［11］FEMA－356 Prestandard and commentary for the seismic rehabilitation of buildings［S］.

［12］DWAIRIH M，KOWALSKY M J，NAU JM.Equivalent damping in support of direct displacement⁃based design［J］.Journal of Earthquake Engineering，2007，11（4）：512⁃530.

［13］GB 50011—2010 建筑抗震设计规范［S］.（GB 50011—2010 Code for seismic design of buildings［S］.（in Chinese））

［14］贡金鑫，高树飞，张勤，等.基于位移的高桩码头抗震设计［R］.大连：大连理工大学，2014（GONG Jin⁃xin，GAOShu⁃fei，ZHANG Qin，et al.Displacement⁃based seismic design of pile⁃supported wharf［R］.Dalian：Dalian University of Technology，2014.（in Chinese））

［15］JTS 146—2012 水运工程抗震设计规范［S］.（JTS 146—2012 Code for seismic design of water transport engineering［S］.（in Chinese）））

［16］ASCE 7－05 Minimum design loads for buildings and other structures［S］.

［17］EMI.Bi⁃linear p⁃y curves for pier 400 piles and pendentwall［R］.Oakland：Fugro West Inc，1999.

［18］APIRP2A－WSD－2005 Recommended practice for planning，designing and constructing fixed offshore platforms—working stress design［S］.

［19］LIYing，GONG Jin⁃xin，ZHANG Yan⁃qing.Pushover analysis for seismic performance of pile⁃supported wharf structures［J］. Journal of Ship Mechanics，2011，15（9）：1022⁃1032.

［20］SHAFIEEZADEH A.Seismic vulnerability assessment ofwharf structures［D］.Georgia：Georgia Institute of Technology，2011.

［21］KAWAMATA Y.Seismic performance of a pile⁃supported container wharf structures in rockfill［D］.Oregon：Oregon State University，2009.

Influencing factors of Pushover analysis for open type wharf w ith standing piles

GAO Shu⁃fei1，GONG Jin⁃xin1，FENG Yun⁃fen2
（1．State Key Laboratory ofCoastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China；2．School of Architecture and Civil Engineering，Liaocheng University，Liaocheng 252059，China）

The nonlinear static analysis method or Pushover analysis method，coinciding with the response spectrum，is of the methods developed in recent years for quantifying the displacements and has been widely applied to seismic design for the open typewharfwith standing piles.The factors influencing the estimation outcome by thismethod is clarified，and the qualitative and quantitative analyses are made between the capacity spectrum method and N2 method as well as the linearization procedures，equivalent damping ratio equations and response spectra used in the capacitymethod.A case study of the open type wharf with standing piles is conducted for the target displacement estimation to investigate the influences of the abovementioned factors.The analysis results show that there exist differences between the outcomes of the capacity method and N2 method and that the extension depends on the equivalent damping ratio equations used in the capacitymethod.For the capacity spectrum method，a great discrepancy arises from the equivalent damping ratio equations and the shape of descent branch of the response spectra，and the linearization method of Pushover curve has played a minor role，that has no great influence upon the calculated results for the displacements.

open type wharf with standing piles；Pushover analysis；target displacements；equivalent damping ratios；linearization methods；response spectra

U656.1＋13

A

1009－640X（2015）05－0001－14

10.16198／j.cnki.1009－640X.2015.05.001

2014－03－25

国家自然科学基金资助项目（51278081）；交通运输部项目“强震区港口工程结构抗震设计研究”（JTSBD 2013 02 130）

高树飞（1989—），男，安徽蚌埠人，博士研究生，主要从事港口工程结构抗震设计研究。

E⁃mail：gaosf1989＠qq.com