异构多种群粒子群优化算法在水位流量关系拟合中的应用

崔东文

（云南省文山州水务局，云南 文山 663000）

异构多种群粒子群优化算法在水位流量关系拟合中的应用

崔东文

（云南省文山州水务局，云南 文山 663000）

通过8个复杂函数对一种异构多种群粒子群优化算法进行仿真验证，并与传统单种群粒子群优化算法进行对比。针对水位流量关系拟合中相关参数难以确定的不足，利用异构多种群粒子群优化算法优化水位流量关系相关参数，以云南省龙潭站、西洋站水位流量关系拟合为例进行实例研究，并与粒子群优化算法、最小二乘法拟合结果进行对比。结果表明：异构多种群粒子群优化算法收敛精度远远优于粒子群优化算法，具有较好的计算鲁棒性和全局寻优能力。该算法对龙潭站和西洋站水位流量关系拟合的平均相对误差绝对值分别仅为0.27%和0.50%，拟合精度优于粒子群优化算法和最小二乘法。利用异构多种群粒子群优化算法优化水位流量关系可以获得更好的拟合效果。

水位流量关系；异构多种群粒子群优化算法；参数优化；盘龙河；西洋江

崔东文.异构多种群粒子群优化算法在水位流量关系拟合中的应用［J］.水利水运工程学报，2015（5）：89－95.（CUIDong⁃wen.Application of convergent heterogeneous particle swarm optimization to fitting stage⁃discharge relation［J］.Hydro⁃Science and Engineering，2015（5）：89－95.）

水位流量关系是指河流某断面的流量与其水位之间的对应状态，通常采用经验曲线、经验方程或表格等形式表达，受水面宽、断面面积、水力比降和糙率等各种水力因素的影响，具有较大的不确定性。提高水位流量关系拟合精度对于水利水电工程规划、水文预测预报以及实行最严格水资源管理制度具有重要意义。目前曼宁公式幂指数法和多项式法常用于构造水位流量关系表达式，其相关参数的选取对于水位流量关系拟合精度有着关键性影响，目前用于水位流量关系参数选取的方法主要有最小二乘法（Least Square Method，LSM）［1］、遗传算法（Genetic Algorithm，GA）［2］、混合禁忌搜索算法（Tabu Search Algorithm，TSA）［3］等，在提高水位流量关系拟合精度上取得了较好的效果。粒子群优化（Particle Swarm Optimization，PSO）算法是近年来发展起来的一种新型进化算法（Evolutionary Algorithms，EA），具有实现容易、精度高、收敛快等优点，并被证明在大多数情况下比GA更有效。然而在实际应用中，传统单种群PSO算法存在易陷入局部最优、收敛较慢等缺点，针对这一缺点，诸多PSO改进方法被纷纷提出，如基于参数选择的改进方法［4－5］、基于混合算法的改进方法［6－9］、基于多种群设计的改进方法［10］以及基于异构多种群策略的改进方法［11］等，均在提升PSO算法收敛性能及收敛速度方面取得了较好效果。其中，基于异构多种群策略改进的PSO算法具有一定优势，对提高PSO算法在实际应用中的求解性能具有重要意义。然而，目前关于PSO算法的异构多种群策略研究中，子群大多采用相同的搜索策略和机制，使得多种群PSO算法的性能提升受到一定限制。文献［12］提出一种新型异构多种群粒子群优化（Convergent Heterogeneous Particle Swarm Optimization，CHPSO）算法，该算法将整个种群分为4个异构但彼此信息共享的子群，各子群采用不同的搜索策略进行搜索，依据不同的信息共享机制在子群之间进行信息共享，最终将子群中最优解作为该算法的全局最优解。

由于多项式型水位流量关系因其图形与大部分观测站的水文特性相符而被广泛采用。因此本文采用多项式型水位流量关系拟合表达式，利用CHPSO算法优化确定多项式系数，并以云南省龙潭站、西洋站水位流量关系拟合为例进行实例研究。主要做法为：一是利用8个复杂函数对CHPSO算法进行验证，并与单种群粒子群优化（PSO）算法进行对比。二是利用CHPSO算法优化确定多项式系数，并与PSO算法、LSM算法拟合结果进行对比。

1 异构多种群粒子群优化算法

异构多种群粒子群优化（CHPSO）算法是文献［12］提出的一种新型粒子群改进算法。其基本原理是：在进化过程中将整个种群分为S1，S2，S3和S4共4个异构但彼此信息共享的子群，各子群采用不同的搜索策略进行搜索，并依据不同的信息共享机制在子群之间进行信息共享，最终将4个子群中最优解作为该算法全局最优解，即

CHPSO算法各子群定义及粒子更新规则如下：

定义1：定义S1和S2为开发搜索的基本子群，其粒子更新策略采用经典粒子群速度及位置的更新方式：

式中：上标（1）／（2）表示基本子群S1和S2；γ1，γ2分别为S1和S2子群的（t＋1）代粒子的适应度值。

定义2：定义S3为自适应子群，采用式（2）进行速度及位置更新：

式中：γ＝γ1＋γ2；r3和r4为分布于［0，1］之间的随机数。

定义3：定义S4为探索子群，采用式（3）进行速度及位置更新：

式中：α1，α2，α3为权重系数，约束于1＝α1＋α2＋α3，本文取α1＝1／6，α2＝1／3，α3＝1／2。

从CHPSO算法可以看出：CHPSO算法基于不同子群粒子更新搜索机制以及信息共享机制，可以有效提高搜索能力和实现局部搜索与全局搜索之间的良好平衡，有利于获得全局最优解。其中，子群S1，S2是子群S3和S4信息更新的基础，S3利用基本子群S1，S2粒子速度及适应度值来更新自身粒子的位置及速度；子群S4是唯一共享所有信息的子群，其利用其他3个子群粒子信息来获得更多的潜在解、保持种群多样性以及探索新的未知空间。文献［12］表明该算法可有效引导粒子趋于全局最优解。

2 CHPSO算法优化水位流量关系的实现步骤

CHPSO算法实现水位流量关系优化的基本思想是：确定水位流量关系表达式，从而确定表达式中待优化系数向量；将CHPSO算法中整个种群平分为4个子群，每个子群粒子所处空间位置均包含一组待优化向量，通过适应度函数来衡量各子群粒子所处空间位置的优劣，并利用式（1）～（3）更新操作来获取各子群最佳函数值对应的粒子空间位置，并将各子群中最佳函数值对应的粒子空间位置作为全局最优解，即待优化系数向量。

CHPSO算法优化水位流量关系的实现步骤可归纳如下：

Step 1确定水位流量关系表达式。本文采用多项式型水位流量关系表达式，其流量与水位关系可用下

式表示：

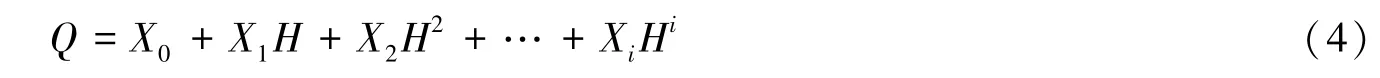
式中：Q为流量；H为与之对应的水位；X0，X1，…，Xi为多项式系数，即为待优化参数。

Step 2确定CHPSO算法的适应度函数。本文选用平均相对误差绝对之和作为适应度函数：

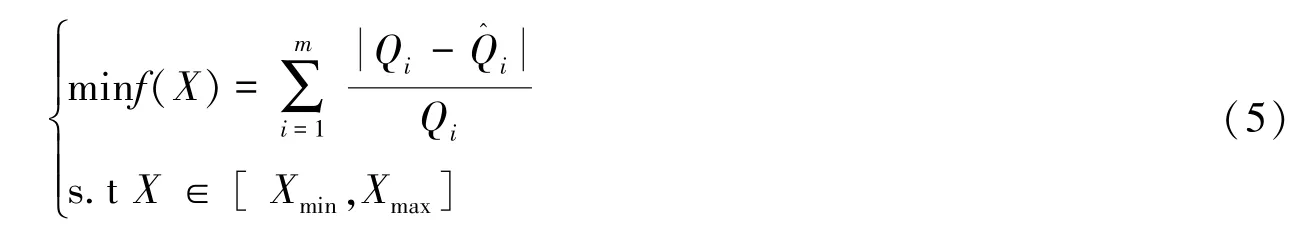
式中：Qi为第i组实测流量；Q＾i为第i组拟合流量；m为水位－流量组数。

Step 3初始化控制参数。设置最大迭代次数，种群规模n，惯性因子ω，局部学习因子、全局学习因子c1，c2，并令初始迭代数t＝1。

Step 4定义子群。将种群规模n平分为S1，S2，S3和S4共4个子群，表示为

和速度Vsk。

Step 6依据式（5）计算各子群粒子的适应度值，并利用式（1）～（3）更新各粒子个体位置，将各子群中个体极值Pi设置为当前位置，群体极值Pg设置为初始群体中最佳粒子的位置。

Step 8比较各子群中粒子适应度值，保留4个子群中粒子个体最优位置

Step 9判断算法迭代终止条件是否满足，如果满足，转向Step10；否则，t＝t＋1，并执行Step6。

Step10算法结束，获得最优位置Pg，即待优化系数向量。

3 算法验证

为客观评价CHPSO算法性能，本文利用8个复杂函数对该算法的性能进行验证，并与PSO算法寻优结果进行对比，见表1。CHPSO算法参数设置为：最大迭代次数T＝2 000，种群规模n＝40；惯性因子ω采用线性递减法，ωmax＝0.90，ωmin＝0.35；局部学习因子、全局学习因子c1＝c2＝1.494 45；探索子群S4位置更新的权重系数分别为α1＝1／6，α2＝1／3，α3＝1／2。PSO算法参数设置为：最大迭代次数T＝2 000，种群规模n＝50，ωmax＝0.90，ωmin＝0.35，局部学习因子、全局学习因子c1＝c2＝1.494 45，个体速度限制为［－0.5，0.5］。

2种算法基于Matlab 2010a用M语言实现，对表1中8个函数重复进行20次寻优计算，见表2。并从最优值、最劣值、平均值、标准差和计算成功率5个方面对2种算法进行评估，当满足式（6）时，即认为当前寻优计算成功。

表1 基准函数Tab.1 Reference functions

（续表）

式中：F为函数的理想最优值；F∗为每次寻优计算所得最优函数值。

表2给出了2种算法的寻优计算统计结果。

表2 函数优化对比结果Tab.2 Function optimization contrast results

从表2可以看出，对各个测试函数两种算法皆独立运行20次的情况下，CHPSO算法收敛精度远远优于PSO算法，其获得的最优值、最劣值、平均值和标准差均比PSO算法的优化结果提高了10个数量级以上，寻优成功率均达到100%。尤其是对Eggcrate，Sphere，Quadric，Griewank，Zakharov，Sumsquares和Schwefel 2.22函数的优化结果比PSO算法提高了100个数量级以上，表现出较高的寻优精度和较好的算法执行能力。其中，CHPSO算法对于Eggcrate，Griewank函数的寻优效果达到了理论最优解，获得的最优值、最劣值、平均值和标准差均为0。

可见，基于不同子群间各异的粒子更新搜索策略以及信息共享机制的CHPSO算法获得了较为理想的寻优效果，同标准PSO算法相比，其优势非常明显，表现出更高的寻优精度和全局搜索能力。

4 实例应用

本文以云南省龙潭站、西洋站2000年32组典型的水位流量数据为例进行实例研究。实测的32组数据见表3。经最小二乘法（LMS）二次、三次、四次和五次多项式拟合比较，当采用四次多项式拟合时LMS算法具有最佳水位流量拟合效果。因此，本文应用CHPSO，PSO及LMS算法对龙潭站、西洋站水位流量四次多项式进行拟合，并选取平均相对误差绝对值ea和最大相对误差绝对值eamax对各算法拟合效果进行评价，其中，CHPSO与PSO算法搜索空间为－100～100，其余参数设置均同上。各算法拟合及比较结果见表4及图1。

表3 2000年实测的32组水位流量数据Tab.3 Measured data of 32 groups of water level and flow discharge in 2000

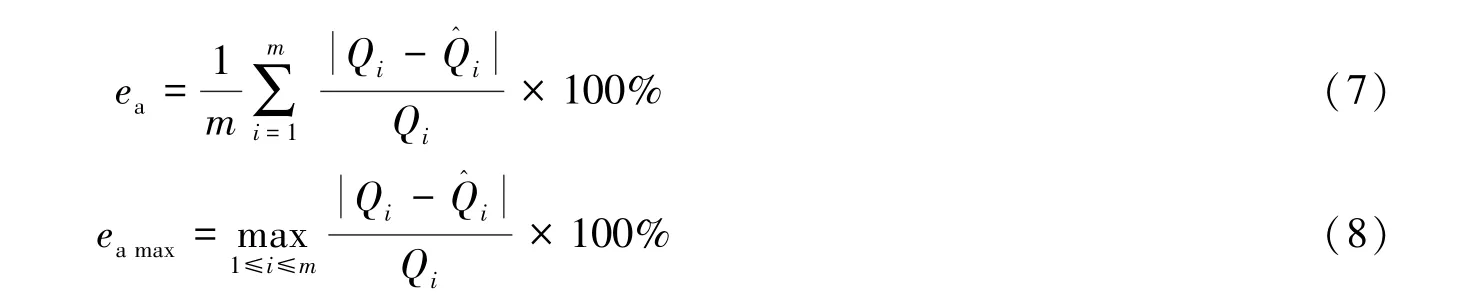
式中：Qi为第i组实测流量；Q＾i为第i组拟合流量；m为水位流量组数。

表4 龙潭站及西洋站水位流量关系拟合及结果比较Tab.4 Water level flow relationship fitting and comparison of results of Longtan and Xiyang stations

从表4可以看出，CHPSO算法对龙潭站水位流量关系拟合的ea，eamax仅为0.27%和0.55%，精度分别比PSO算法和LMS算法提高了50.9%和48.1%；对西洋站水位流量关系拟合的ea，eamax仅为0.50%和1.64%，精度分别比PSO算法和LMS算法提高了81.5%和47.4%。拟合精度均优于PSO算法和LMS算法，表明CHPSO算法具有较好的收敛精度和全局寻优能力，利用CHPSO算法优化水位流量关系可以获得更好的拟合效果。从图1来看，基于CHPSO算法的流量拟合结果相对误差最小，其次是LMS法，基于PSO算法的流量拟合误差相对较大。

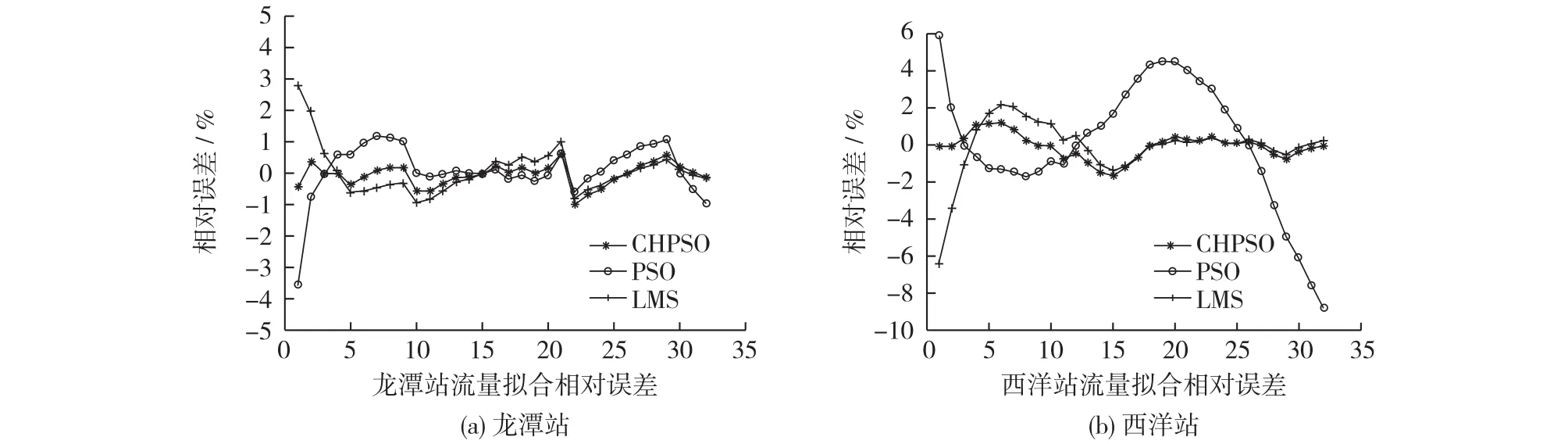
图1 龙潭站和西洋站流量拟合相对误差Fig.1 Flow fitting relative errors for Longtan and Xiyang station

5 结 语

（1）介绍了新型异构多种群粒子群优化（CHPSO）算法，通过8个高维复杂函数对该算法进行对比验证。结果表明基于不同子群间各异的粒子更新搜索策略以及信息共享机制的CHPSO算法具有更好的收敛精度和全局寻优能力。

（2）提出CHPSO算法优化水位流量关系的步骤及方法，利用CHPSO算法优化水位流量关系，不但提高了水位流量关系的拟合精度，而且为解决水位流量关系相关参数寻优问题提供了一种全新的途径和方法。

（3）从2个实例的拟合结果来看，CHPSO算法的拟合精度优于PSO算法及LMS算法，可为相关水位流量关系拟合提供借鉴和参考。

［1］戴凌全，戴会超，蒋定国，等.基于最小二乘法的河流水位流量关系曲线推算［J］.人民黄河，2010，32（9）：37⁃39.（DAI Ling⁃quan，DAIHui⁃chao，JIANG Ding⁃guo，etal.Relationship curve of riverwater level flow based on least squaremethod［J］. Yellow River，2010，32（9）：37⁃39.（in Chinese））

［2］杨晓华，陆桂华，郦建强.自适应加速遗传算法及其在水位流量关系拟合中的应用［J］.水文，2002，22（2）：14⁃18.（YANG Xiao⁃hua，LU Gui⁃hua，LI Jian⁃qiang.Adaptive accelerating genetic algorithm and in the stage discharge relation fitting［J］.Hydrology，2002，22（2）：14⁃18.（in Chinese））

［3］汪嘉杨，李祚泳，倪长健，等.基于混合禁忌搜索算法的水位流量关系拟合［J］.系统工程，2006，24（6）：107⁃110.（WANG Jia⁃yang，LIZuo⁃yong，NIChang⁃jian，et al.Fitting ofwater level flow relationship based on hybrid tabu search algorithm［J］. System Engineering，2006，24（6）：107⁃110.（in Chinese））

［4］赵远东，方正华.带有权重函数学习因子的粒子群算法［J］.计算机应用，2013，33（8）2265⁃2268.（ZHAO Yuan⁃dong，FANG Zheng⁃hua.Particle swarm optimization algorithm with weight function's learning factor［J］.Journal of Computer Applications，2013，33（8）2265⁃2268.（in Chinese））

［5］郜振华，梅莉，祝远鉴.复合策略惯性权重的粒子群优化算法［J］.计算机应用，2012，32（8）：2216⁃2218.（GAO Zhen⁃hua，MEI Li，ZHU Yuan⁃jian.Particle swarm optimization algorithm with composite strategy inertia weight［J］.Journal of Computer Applications，2012，32（8）：2216⁃2218.（in Chinese））

［6］余玉丰，李国，徐晨.基于分组的PSO与DE的混合算法［J］.计算机应用究研究，2014，31（8）：2294⁃2298.（YU Yu⁃feng，LIGuo，XU Chen.Hybrid algorithm based on grouped PSO and DE［J］.Application Research of Computers，2014，31（8）：2294⁃2298.（in Chinese））

［7］刘朝华，张英杰，章兢，等.一种双态免疫微粒群算法［J］.控制理论与应用，2011，28（1）：65⁃72.（LIU Zhao⁃hua，ZHANGYing⁃jie，ZHANG Jing，et al.A two⁃state immune particle swarm optimization algorithm［J］.Control Theory＆Applications，2011，28（1）：65⁃72.（in Chinese））

［8］林国汉，章兢，刘朝华.免疫综合学习粒子群优化算法［J］.计算机应用研究，2014，31（11）：3229⁃3233.（LIN Guo⁃han，ZHANG Jing，LIU Zhao⁃hua.Immune comprehensive learning particle swarm optimization algorithm［J］.Application Research of Computers，2014，31（11）：3229⁃3233.（in Chinese））

［9］郭一楠，程健，曹媛媛，等.基于混沌知识迁移的多种群粒子群文化算法［J］.控制理论与应用，2011，28（9）：1056⁃1062.（GUO Yi⁃nan，CHENG Jian，CAO Yuan⁃yuan，et al.Multi group particle swarm culture algorithm based on chaotic knowledge transfer［J］.Control Theory＆Applications，2011，28（9）：1056⁃1062.（in Chinese））

［10］刘衍民，隋常玲，赵庆祯.基于K⁃均值聚类的动态多种群粒子群算法及其应用［J］控制与决策，2011，26（7）：1019⁃1025.（LIU Yan⁃min，SUI Chang⁃ling，ZHAO Qing⁃zhen.Dynamic multi⁃swarm particle swarm optimizer based on K⁃means clustering and its application［J］.Control and Decision，2011，26（7）：1019⁃1025.（in Chinese））

［11］倪庆剑，邓建明，邢汉承.基于异构多种群策略的动态概率粒子群优化算法［J］模式识别与人工智能，2014，27（2）：146⁃152.（NI Qing⁃jian，DENG Jian⁃ming，XING Han⁃cheng.Dynamic probabilistic particle swarm optimization based on heterogeneousmultiple population strategy［J］.Pattern Recognition and Artificial Intelligence，2014，27（2）：146⁃152.（in Chinese））

［12］CHEUNG N J，DING Xue⁃ming，SHEN Hong⁃bin.Convergent heterogeneous particle swarm optimization for Takagi⁃Sugeno fuzzy modeling［J］.IEEE Trans on Fuzzy System，2014，22（4）：919⁃933.

Application of convergent heterogeneous particle swarm optim ization to fitting stage⁃discharge relation

CUIDong⁃wen
（Wenshan Water Conservancy Bureau of Yunnan Province，Wenshan 663000，China）

By use of 8 complex functions，a heterogeneous multi group particle swarm optimization algorithm is simulated，comparing with the traditional single population particle swarm optimization algorithm.Aiming at the deficiencies of the stage discharge relation fitting in it is difficult to determine the parameters，using a variety of the heterogeneous particle swarm optimization algorithm for optimizing the relative parameters of the stage⁃discharge relationship，taking stage⁃discharge relation fitting of Yunnan Province Longtan station，Xiyang station as case studies，and the particle swarm optimization algorithm and least squares fitting results are compared in the study. The analysis results show that the convergence accuracy of the heterogeneous multi group particle swarm optimization algorithm is much better than the particle swarm optimization algorithm，with good computational robustness and global optimization ability.The relative error absolute values of the fitting for the relationships between the water level of the Longtan railway station and the Xiyang station are only 0.27%and 0.50% respectively.The fitting accuracy is better than that of the particle swarm optimization and the least squaremethod. The better fitting effect can be obtained by optimizing the water level flow relationship by using the heterogeneous multi group particle swarm optimization algorithm.

stage⁃discharge relation fitting；convergent heterogeneous particle swarm optimization algorithm；parameter optimization；Panlong River；Xiyang River

P337－3

A

1009－640X（2015）05－0089－07

10.16198／j.cnki.1009－640X.2015.05.012

2015－02－05

崔东文（1978—），男，云南玉溪人，高级工程师，主要从事水资源水环境研究及水资源保护等工作。E⁃mail：cdwgr＠163.com.