一种基于RSSI的三角形质心改进算法

于 泉，徐保国

（江南大学 物联网工程学院，江苏 无锡 214122）

无线传感器网络节点定位研究受到国内外学者的广泛关注，根据定位时是否需要测量距离，定位算法可分为基于测距（Range—Based）算法和无需测距（Range—free）算法[1]。 基于测距的定位算法利用测量的距离或角度信息等进行定位运算，常用的测距技术主要有 RSSI[2]、TOA、TDOA、AOA[3]，无需测距通常根据网络连通性进行定位，无需测距的算法主要有质心算法、DV－Hop算法、APIT算法、MDS算法。基于测距的定位算法需要附加的设备，提高了设备成本和通信开销大，无需测距算法由于对设备要求低，计算简单和通信开销小等优点，成为无线传感器网络定位研究的热点。无需测距定位的算法因在成本、功耗等方面的优势，受到越来越多的关注。

1 传统定位算法模型

1.1 传统质心算法

南加州大学的Nirupama Bulusu等人[4]提出一种基于网络连通性无需测距的质心定位算法，主要思路举例体现，假设未知节点F在A1…An为锚节点组成的多边形中，锚节点坐标分别为（x1，y1）～（yn，yn），则未知节点 F 坐标为：

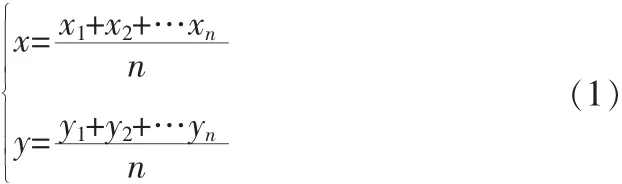
传统质心算法的计算量和通信开销较少，原理简单容易实现，受到广泛研究，但其对传感器节点密度和均匀度依赖强，质心算法受这两个因素影响较大，当锚节点接受的信息方差较大时，定位精度会变得比较低，定位精度有待提升，文献[5]提出了基于RSSI的三角形质心算法，三角形面积减小，定位精度得到一定提升；文献[6]利用三角形三边的垂直平分线，划分6个区域，通过比较三锚节点接收的信号强度，确定未知节点所在的区域；上述算法都是通过缩小未知节点所在三角形的面积，提高定位的精度，本文思路大致相同，通过连接三边中点划分16或10个区域，利用外心的适应度值大小确定未知节点所在区域，同样提升了定位精度。

1.2 RSSI测距技术

RSSI的测距，接收节点根据收到信号强度，计算信号传输损耗，利用信号的经验模型或理论模型将传输损耗转化为距离[7]。信号的经验模型是匹配建立在各个点上的位置与信号强度的数据库，理论模型通常采用的是无线电传播损耗模型，常用的传播路径损耗模型有：对数－常态分布模型和自由空间无线电传播路径损耗模型，采用对数－常态分布模型[8]，即

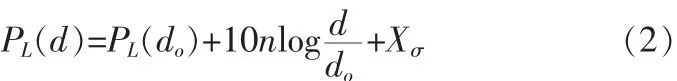
其中，PL（d）为信号传输距离 d 的路径损耗，PL（do）为信号传输距离do的路径损耗，n为信号衰减参数，通常取2～5，Xσ为期望为0标准差为σ的高斯分布。未知节点接收到锚节点信号强度为：

2 改进的三角形质心算法

如图1所示未知节点D在三个锚节点组成的锐角三角形内，A1、A2、A3分别为 AB、AC、BC 的中点， 则 4 个小三角形两两全等，外接圆的半径也相同，假设点D是两平行线A1A2、A4A5之间的任意一点，作DE垂直 A1A2，则∠P1DE为钝角，连接 P1E、P2E，点 O 为 A1A2的中点，连接 P1O、P2O，P1、P2分别为三角形A A1A2和三角形A1A2A3的外心，圆心到弦中点的直线垂直平分弦，即P1O、P2O垂直平分A1A2，所以，P1E=P2E，因为∠P1DE为钝角，所以P1E>P1D，所以P1E>P1D，即点D到三角形A A1A2的外心比到三角形A1A2A3的外心距离要小，三角形内的其他点，即三角形A A3A4内的点，到P1的距离明显比到P2的距离小，得出三角形A A1A2内的点到外心的距离中，到P1的距离最小。其它相邻三角形的判断与上述同理，判断未知节点在锚节点组成的三角形内后，连接三边中点，计算小三角形的外心，然后比较未知节点到四个外心的距离，得到距离最近的外心，它所在的小三角形就是未知节点所在区域，继续按此原理划分区域，最终把三角形划分了16个区域，通过判断未知节点到哪一外心距离最小，来判断其所在的小三角形，但是未知节点坐标未知，无法计算其到外心的距离，受到定位算法中适应度值[9]计算的启发，距离未知节点越近，适应度越小，确定未知节点所在小三角形后，得到小三角形质心，质心为未知节点估计坐标。

适应度值计算公式为：

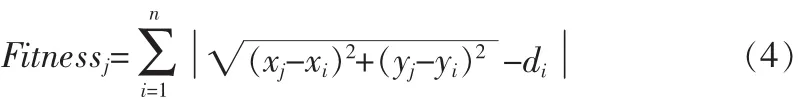
式中：（xj，yj）为小三角形的外心坐标，（xi，yi）为 i锚节点坐标，di为未知节点到i锚节点的距离，n为锚节点数量。

所有患者均给予常规对症治疗,吸氧、服用阿司匹林、阿托伐他汀,控制血压、血糖,根据颅内压情况酌情给予甘露醇脱水治疗,并给予改善微循环、抗感染维持水、电解质平衡等治疗。在此基础上,对照组给予依达拉奉注射液(吉林省辉南长龙生化药业股份有限公司,国药准字H20080592)30 mg加入生理盐水100 m L中静脉滴注,2次/d。观察组在对照组基础上服用丁苯酞软胶囊(石药集团恩必普药业有限公司,国药准字H20050299)0.2 g/次,3次/d。14 d为1个疗程,1个疗程后评价疗效[3]。

未知节点在三锚节点组成的直角三角形时，连接三边中点，其中两个小三角形的外心重合，先判断这3个外心适应度值最小者。如果重合的外心适应度值最小，把所在的区域缩小为矩形区域，再把矩形区域平分成4个小矩形，求出其外心坐标及其适应度值，得到适应度值最小的外心，相应的小矩形的质心为估计位置。如果另外两个小三角形外心适应度值最小，连接三边中点，重合外心的两个小三角形作为一个区域参与判断，最终直角三角形被分成10个三角形或矩形，如图2所示，P1～P10为10个三角形或矩形的外心，若顶点A、B、C坐标后计算P1～P10的适应度值，判断未知节点在哪一小三角形后，求出三角形的质心，质心则为未知节点的估计坐标。

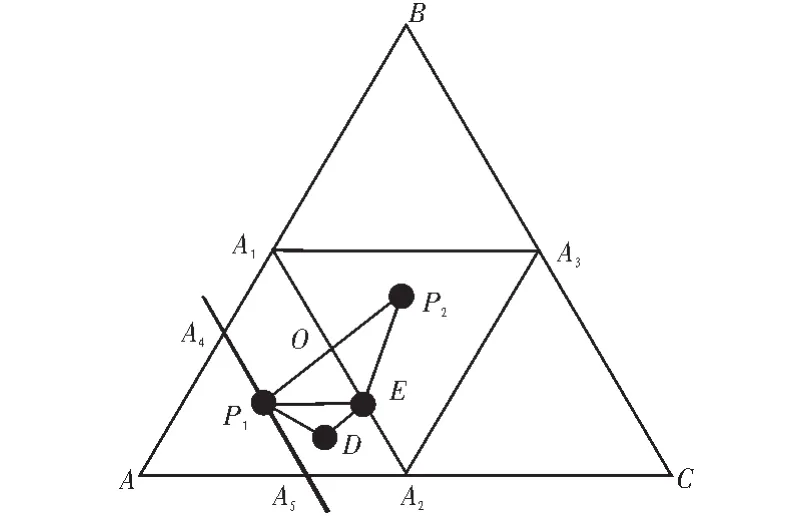
图1 未知节点在锐角三角形中Fig.1 The unknown node in acute triangle

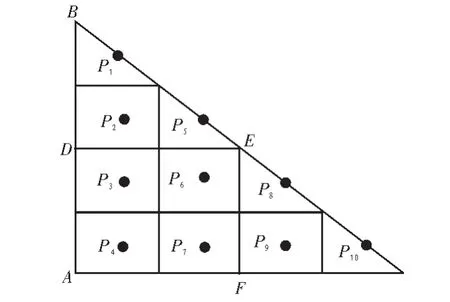
图2 未知节点在直角三角形中Fig.2 The unknown node in right triangle

未知节点在3个锚节点组成的钝角三角形中时，与锐角三角形情况不同的是，两个小三角形的外心在相邻的三角形中，如图3所示，D、E分别为三角形P1P2P3、P1B P3的外心，未知节点F在三角形P1B P3内，距离三角形P1B2P3的外心最近，未知节点F在三角形P1P2P3内时，距离三角形P1B P3的外心最近。先判断三角形P1A P2、P2CP3、P1P2P3外心的适应度值，若判断未知节点在三角形P1P2P3内，未知节点也可能在三角形P1B P3内，再比较外心D、E的适应度值，若D适应度值小，未知节点在三角形P1BP3内，若E适应度值最小，未知节点在三角形P1P2P3内，连接三边中点，继续划分小三角形。若未知节点在三角形P1A P3或三角形P1CP3内，继续连接中点划分三角形，最终三角形被划分为16个小三角形。

在100×100 m矩形区域随机分布50个传感器节点，取其中一个作为参考点，取距离参考节点h的圆上点，从弧度0～6.2选取63个点，得到适应度值曲线，如图4所示，距离未知节点相同的适应度值是波动的，并不是恒定不变的，距离相差大的时候，距离越小适应度值越小，但是当距离相差不大时，适应度值曲线会有交点，距离大的适应度值不一定大，存在一定误差，会造成上述判断错误，降低定位精度。

图3 未知节点在钝角三角形中Fig.3 The unknown node in obtuse triangle

图4 距离不同的适应度值曲线Fig.4 Fitness value curve in different distance

以一个锐角三角形特列仿真实验，三角形面积为32 m2，在三角形内随机取100个点，验证算法是否准确，实验100次取平均，求得判断准确率为30.25%，造成误差的主要原因是距离不变时适应度值不稳定，会造成判断所在的小三角形和实际所在的小三角形不同，由于只有在距离相差少时才会造成判断错误，所以两个小三角形往往是邻居，上述的锐角三角形特例实验中，也得出了定位误差小于1 m的点达到80.63%，判断误差一定程度上提高了定位精度，说明本算法的可行性。

3 算法步骤

1）锚节点向周围环境周期性广播包含自身ID和位置坐标的信息。

2）未知节点收到锚节点广播的信息后，对同一个锚节点的RSSI值[11]，取多个RSSI数据的均值，作为其接收的RSSI值；

3）未知节点接收锚节点广播的信号，并建立3个集合:锚节点集合：B_Set={b1，b2，…，bn}；未知节点到锚节点距离集合：D_Set={d1，d2， …，dn}； 锚节点位置集合：P_Set={（x1，y1），（x2，y2），…（xn，yn）}；

4）未知节点从集合中选择距离未知节点小于通信半径R的锚节点，然后从选取的锚节点中任意选择三个组成三角形，构成一个3角形集合，分别采用添加计数器的PIT测试[10]，选出内含未知节点的三角形集合，记为：T_Set={（b1，b2，b3），（bi，bj，bk）…}，若选取的锚节点数小于 3，利用传统质心算法来定位；

5）判断三角形是锐角三角形、直角三角形或钝角三角形，然后分别采用上述方法求出未知节点的坐标集{（xe1，xe1），（xe2，xe2）…（xep，xep）}。

6）取坐标集合{（xe1，xe1），（xe2，xe2）…（xep，xep）}的期望，即其中，（x，y） 是未知节点的坐标。

4 仿真结果及分析

通过Matlab R2010b进行仿真，同时仿真传统质心算法和本文优化的三角形质心算法，来验证算法的性能。评估算法性能指标为平均定位误差。

其中定位误差为：

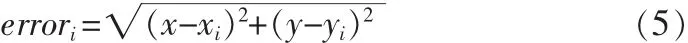
式中：（x，y）为算法估计未知节点 i的坐标，（xi，yi）为未知节点i的真实坐标。

平均定位误差为：

式中：n为未知节点数量，R为通信半径。

节点分布越均匀、密度越大，定位精度越高，每次实验的均匀度和密度不同，这些因素会影响实验结果，因此实验100次取平均值更合理，更能体现算法的定位效果。如图5所示，传感器节点数量50，通信半径20 m，调节锚节点比列，锚节点比例越大平均定位误差越小，本文算法的平均定位误差降低了15.47%。如图6所示，锚节点比例保持40%、通信半径20 m，传感器节点越多平均定位误差越小，本文算法的平均定位误差降低了15.21%，最高降低了17.80%。如图7所示，传感器节点50，锚节点20个，调节通信半径，本文算法的平均定位误差降低了11.70%，通信半径越大，两者定位误差差距有扩大趋势。上述实验表明锚节点比例越大、传感器节点数量越多、通信半径下越大，平均定位误差越小，本文算法的定位精度提升明显。

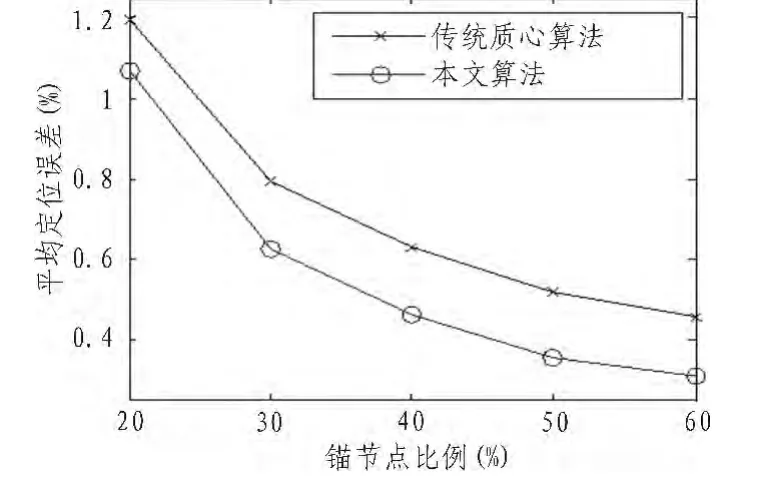
图5 锚节点比例不同时的误差Fig.5 Error of different anchor node proportion

如图8所示，在60×60 m矩形区域中随机分布50个传感器节点，锚节点25个，通信半径20 m，图示25个未知节点的误差图，传统质心算法节点误差的期望为11.479 4 m，方差为38.030 1，本文算法的节点误差期望为6.606 4 m，方差为29.007 2。可以看出，本文算法相比传统质心算法精度提升明显，稳定性也得到了一定的提高。

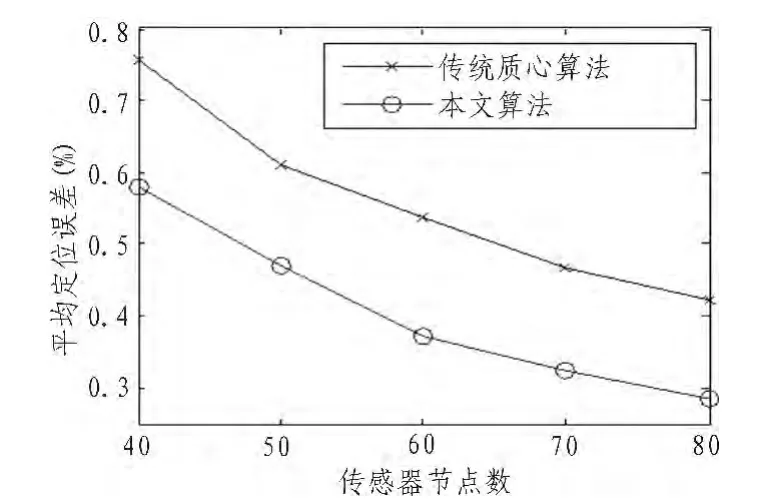
图6 节点数量不同时的误差Fig.6 Error of different number of nodes

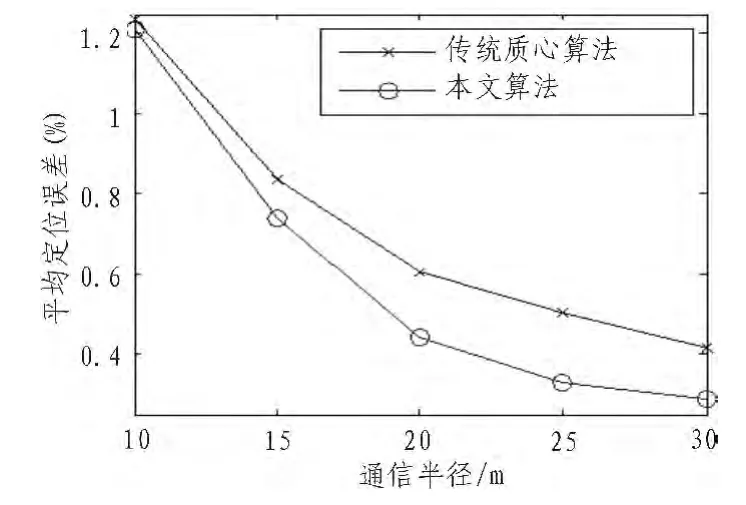
图7 通信半径不同时的误差Fig.7 Error of different communication radius

图8 节点误差图Fig.8 Node error figure

5 结 论

传统质心算法计算简单、通信开销少，但对网络环境依赖程度较高，定位精度也有待提升，本文算法把内含未知节点的三角形划分16或10个区域，利用外心适应度值的大小，来确定未知节点所在区域，三角形面积减小，定位精度变高，通过matlab仿真得出：本文算法的定位精度提升明显，平均定位误差最高降低了17.80%，稳定性也得到一定提升。

[1]刘锋，章登义．基于RSSI的无线传感器网络质心定位算法[J]．计算机科学，2012，39（6A）：96-98.LI Feng，ZHANG Deng-yi. The centroid localization algorithm based on RSSI for Wireless sensor network[J].Computer Science，2012，39（6A）:96-98.

[2]Lu thy K A，E Grant D，Henderson T C.Leveraging RSSI for Robotic Repair of D is connected Wireless Sensor Networks[C]//Proceedings of 2007 IEEE In tern at ion al Conference on Robotics and Automation.Rome， Italy，2007:10-14.

[3]刘姗，冷文，王安国，等.一种基于RSSI的AOA估计算法[J].传感器与微系统，2013，32（11）：132-134.LIU Shan，LENG Wen，WANG An-guo，et al.An AOA estimation algorithm based on RSSI[J].Transducer and Microsystem Technologies，2013，32（11）:132-134.

[4]Nirupama Bulusu，John Heidemann，Deborah Estrin.Adaptive Beacon Placement[C]//In Proceedings of the 21st International Conference on Distributed Computing Systems.Mesa:[s.n.]，2001:489-498.

[5]林玮，陈传峰.基于RSSI的无线传感器网络三角形质心定位算法[J]．现代电子技术，2009，289（2）：180-182.LINWei，CHENChuan-feng.The triangle centroid localization algorithm based on RSSI for wireless sensor network[J].Modern Electronic Technology，2009，289（2）:180-182.

[6]Yu Liu，Xiao Yi，You He．A Novel Centroid Localization for Wireless Sensor Networks [J].International Journal of Distributed Sensor Networks，2012，2012：1-8．

[7]孙利民，李建中，陈渝，等.无线传感器网络[M].北京：清华大学出版社，2005.

[8]孙懋珩，廖根健．WSNs中基于粒子群优化的节点定位算法[J].测控技术，2011，30（12）：111-115.SUN Mao-hang，LIAO Gen-jian.Node localization algorithm based on particle swarm optimization In WSNs[J].Measurement and Control Technology，2011，30（12）:111-115.

[9]李牧东，熊伟，梁青.基于人工蜂群改进算法的无线传感器网络定位算法[J].传感技术学报，2013，26（2）：241-245.LI Mu-dong，XIONG Wei，LIANG Qing.Wireless sensor networks node localization algorithm based on improved ABC algorithm[J].Chinese Journal of Sensors and Actuators，2013，26（2）:241-245.

[10]王新生，廖世奇.基于区域分割的无线传感器网络定位算法[J].计算机应用与软件，2013，30（4）：231-234.WANG Xin-sheng，LIAO Shi-qi.Wireless sensor network localization algorithm based on region segmentation[J].Computer Applications and Software，2013，30（4）:231-234.

[11]张铮，饶志训，黄志峰.无线传感器网络中RSSI滤波的若干处理方法[J].现代电子技术,2013(20):4-6,10.ZHANGZheng，RAOZhi-xun，HUANGZhi-feng.Someprocessing methods of RSSI filtering in wireless sensor network[J].Modern Electronics Technique，2013（20）:4-6，10.