基于模糊层次分析法的太阳能系统在封场后填埋场的应用

王 渡，江剑明，陈德珍

(1.上海电力学院 能源与机械工程学院，上海 200090;2.同济大学 热能与环境工程研究所，上海 200092)

填埋法是最早对垃圾进行处理的方法之一.到目前为止，在中国有成百上千座垃圾填埋场，它们分布在许多城市的周围，占用了大量的土地.如果不对封场后的垃圾填埋场进行合理规划，将会导致城市土地使用的紧张和混乱.自1999年以来，中国的城市固体废弃物填埋场的数量已经从549座减少到409座.因此，在过去的10多年里，至少有140座左右的垃圾填埋场被关闭封场，[1-4]这意味着有数十万亩的土地可以被再利用.

随着城市化进程的发展，对于土地的需求也在日益增加，而封场后垃圾填埋场的土地的潜在价值被逐渐开发利用.然而我国对于封场后垃圾填埋场的土地和资源利用的研究只是最近几年才展开，且大部分研究的重点集中于理论思想和观点，部分研究还只是处于实验室阶段.[5-7]近年来，在封场后垃圾填埋场上也有了几个工程应用的案例，大部分是植被复耕方案.由于政府鼓励对包括封场后垃圾填埋场在内的土地进行再利用，若在这些地区安装可再生能源装置将会受到欢迎.

在封场后垃圾填埋场安装太阳能发电系统有3个重要的优势:一是封场后垃圾填埋场可以提供上万亩的空闲土地用于太阳能系统的安装，而这些土地在近期是无法用于商业开发的;二是封场后的填埋场具有更低的土地交易成本;三是在闲置土地上发展清洁的太阳能发电系统可以减轻在其他地方安装清洁能源的压力.

本文针对封场后垃圾填埋场上太阳能发电系统，从技术可行性、经济效益和环境保护3个方面进行研究，通过模糊层次分析法建立了封场后垃圾填埋场上太阳能发电系统的决策模型.

1 模糊层次分析法

层次分析法是在20世纪70年代由美国学者首先提出的，[8-10]它是一个实践性很强的分析决策模型，将定性和定量的分析结合在一起.用层次分析法作系统分析时，首先将问题层次化，根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，然后按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型.最终将系统分析归结为最底层(供决策的方案)，相对于最高层(总目标)的相对重要性权值的确定或相对优劣的排序问题.此外，该方法对于解决目标结构非常复杂且所需数据缺乏的决策问题十分有效，因此该方法日益得到广泛的重视和使用.但在遇到不确定性和模糊性因素较多的问题时，层次分析法很可能受到决策者主观判断的影响，与实际情况偏差较大.

针对上述问题，本文提出采用基于三角模糊数的层次分析法来评价封场后垃圾填埋场的太阳能利用系统，对判断矩阵的各元素进行模糊化，使所得结果更符合实际.

根据层次分析法建立阶梯层次结构后，目标层与准则层元素的隶属关系就已确定.决策者依据确定评价指标的判断矩阵，对因素x1和 x2的重要性进行比较，一般使用9点的比例标度来对比较后的重要性进行赋值.其中，1，3，5，7，9 分别表示相同重要、明显重要、相当重要、强烈重要和极端重要;而2，4，6，8为上述相邻判断的中值.

令aij为模糊判断矩阵中第i个评价准则相对第j个评价准则的重要程度值，用aij=(l，m，u)表示，反之，aij－1=(1/u，1/m，1/l)，构造模糊评判矩阵A=(aij)n×n.

考虑决策问题的复杂性、个人喜好、语言判断的模糊性和不确定性等因素，认为评价指标的判断矩阵皆为模糊信息，其判断结果在一定的模糊程度内是一个重要度等级范围，因此基于表1对判断矩阵进行模糊化处理.表1中，λ为每次判断的模糊度等级(取λ=1，2)，本文取λ=1.

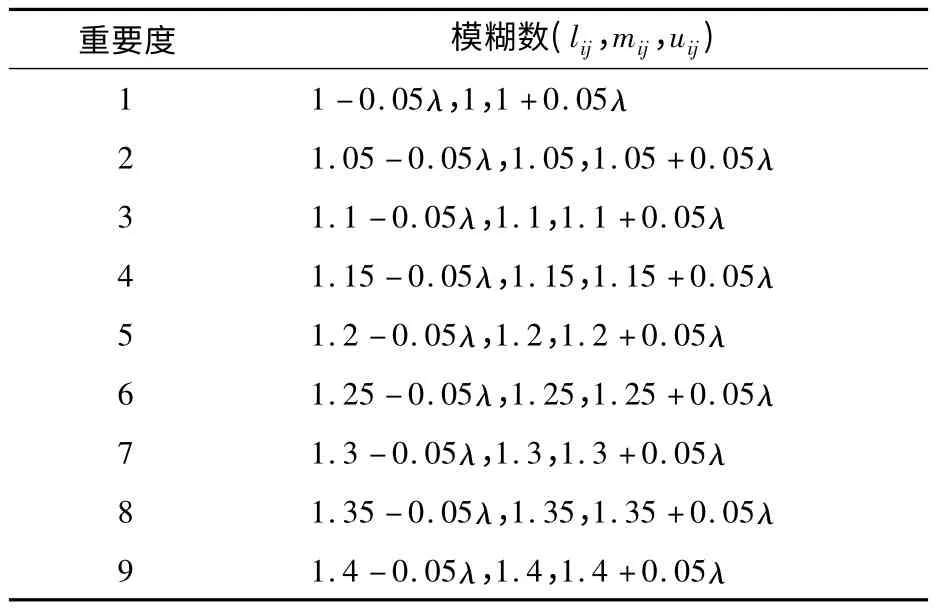
表1 判断矩阵元素模糊化的前后对照

利用三角模糊数的相关定理可确定相关指标的权重值.在构造的模糊判断矩阵中，指标Si表示模糊判断矩阵中第i个评价准则相对其他所有准则的综合重要程度值，其表达式为:

设S1=(l1，m1，u1)和S2=(l2，m2，u2)是两个三角模糊数，V(S1≥S2)表示三角模糊数S1≥S2的可能程度，V(S≥S1，S2，S3，…，Sn)表示三角模糊数S大于等于n个三角模糊数Si的可能程度，令d＇(C i)表示一个指标C i优于其他准则的纯测量度M，则有:

于是，可得所有准则的权重向量为:

经过归一化处理，可得每个准则的归一化权重值为:

2 项目分析

2.1 构造层次结构

本文将分析层次模型分为目标层、准则层和项目层3个层次，如图1所示.将封场后垃圾填埋场上最合适的太阳能系统作为目标层，包括环境因素、技术条件和经济效益在内的3个评估因素作为准则层.项目层被分为多晶硅太阳能光伏系统、柔性薄膜太阳能光伏系统和碟式太阳能热发电系统[11-15]3个具体的方案.

图1 层次模型结构示意

2.2 构造判断矩阵

在工程应用中，技术方面需要考虑设备的安装以及安全可靠性，而整个太阳能发电系统的经济效益问题对系统整体方案的确定影响最小.因此，构造判断矩阵如下:

在经济性分析中需要考虑太阳能系统的投资成本和运行成本.在3个方案中，碟式太阳能热发电系统的投资成本和运行成本最大，而柔性薄膜太阳能光伏系统的成本最小.不同权重由成本来决定，故判断矩阵如下:

技术条件的评估主要考虑效率、风载、雨雪等因素.多晶硅太阳能光伏系统的效率高于柔性薄膜太阳能光伏系统，但抵御风雪的能力较差.根据综合评估得出判断矩阵如下:

环境因素分析主要与支撑系统的重量、阴影、渗滤液等因素有关.柔性薄膜太阳能光伏系统的重量最轻，而且它所带来的环境影响也最小.根据综合分析得出判断矩阵如下:

2.3 目标层权重计算

以矩阵A为例，说明权重的求解过程.

根据式(1)，计算B1层的综合重要程度:

同理，可以得到

因此，根据式(2)、式(3)和式(4)，可以分别计算得到:

同理:

计算可得W'=[0.5，0.75，1]，经归一化处理，W=[0.223，0.333，0.444].同理，可以求得各个项目层与目标层的权重值，见表2.

表2 太阳能系统应用权重

2.4 3个方案的排序结果

根据表2计算可以得到3个方案的结果，多晶硅太阳能光伏系统为0.22，柔性薄膜太阳能光伏系统为0.51，碟式太阳能热发电系统为0.21.

根据上述分析，在封场后垃圾填埋场上建立太阳能系统方案的排序结果为:柔性薄膜太阳能光伏系统＞多晶硅太阳能光伏系统＞碟式太阳能热发电系统.由此可见，柔性薄膜太阳能光伏系统最适合在封场后垃圾填埋场上应用.

3 结语

模糊层次分析法能够克服传统层次分析法的局限性，使权重的客观性和准确性得到更好的保证，对不同方案的定性问题进行定量分析.本文从环境、技术和经济3个角度，通过模糊层次分析法对封场后垃圾填埋场上布置太阳能系统的方案决策建立了模型.3个方案的结果分别为 0.22，0.51，0.21.由结果可知，在封场后垃圾填埋场上最适合采用柔性薄膜太阳能光伏系统.

[1]CHEN Jiali，LI Xuejian.The research of bank performance evaluation based on principal component analysis and analysis hierarchy process(AHP)[J].Journal of Systems Science，2011，19(1):74-76.

[2]WINRNEBRAKE J J，CRESWICK B P.The future of hydrogen fueling systems for transportation:an application of perspective-based scenario analysis using the analytic hierarchy process[J]. Technological Forecasting and Social Change，2003，70(4):359-384.

[3]SAATY T.Decision making with the analytic hierarchy process[J]. International Journal of Services Sciences，2008，1(1):83-98.

[4]SAATY T L.The analytic hierarchy process:planning，priority setting，resource allocation[M].London:McGraw-Hill International Book Co.，1980:56-62.

[5]MILLS D.Advances in solar thermal electricity technology[J].Solar Energy，2003，76(1-3):19-31.

[6]COLLADO F J.Quick evaluation of the annual heliostat field efficiency[J].Solar Energy，2008，82(4):379-384.

[7]MILLS D.Compact linear Fresnel reflector solar thermal power plants[J].Solar Energy，2000，68(3):263-283.

[8]TAGGART S.CSP:dish projects inch forward[J].Renewable Energy Focus，2008，9(4):52-54.

[9]RAMANATHAN R，GANESH L S.Energy resource allocation incorporating qualitative and quantitative criteria:an integrated model using goal programming and AHP[J]. Socio-Economic Planning Sciences 1995，29(3):197-218.

[10]WALLENIUS J，JAMES S，PETER C .Fishburn，et al.Multiple criteria decision making，multiattribute utility theory:recent accomplishments and what lies ahead[J]. Management Science，2008，54(7):1 336-1 349.

[11]QU H，ZHAO J，YU X，et al.Prospect of concentrating solar power in China-the sustainable future[J]. Renewable and Sustainable Energy Reviews，2008，12(9):2 505-2 514.

[12]KOMENDANTOVA N，ANTHONY Patt，LUCILE Barras，et al.Perception of risks in renewable energy projects:the case of concentrated solar power in north Africa[J].Energy Policy，2009(12):2 008.

[13]LI J. Scaling up concentrating solar thermal technology in China[J]. Renewable and Sustainable Energy Reviews，2009，13(8):2 051-2 060.

[14]FAUSTO C.Fuzzy TOPSIS approach for assessing thermalenergy storage in concentrated solar power systems[J]. Applied Energy，2010，87(2):496-503.

[15]XU Y L，JOHN F.Developing a risk assessment model for PPP projects in China—A fuzzy synthetic evaluation approach[J].Automation in Construction，2010，19(7):929-943.