不同理论公式预测粘性土地基极限承载力比较

包松考，王启贵，杨梅萍

（1.浙江省温州市瓯江口开发建设投资集团有限公司，浙江温州，325000；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州，310014）

不同理论公式预测粘性土地基极限承载力比较

包松考1，王启贵2，杨梅萍2

（1.浙江省温州市瓯江口开发建设投资集团有限公司，浙江温州，325000；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州，310014）

基于文献中实测的载荷试验数据和计算数据，采用有限元软件ABAQUS建立三维模型进行计算分析，对Vesic、Hansen和Meyerhof三个理论公式预测粘性土地基极限承载力进行了比较，讨论了基础尺寸、基础埋深、土性参数等因素对预测结果的影响。结果表明：（1）这三个公式预测粘性土浅基础（D＜B）极限承载力误差相对较小，但均不适用于粘性土深基础（D＞B）。（2）对于粘性土浅基础，三个公式预测值总体上均偏大，一般Meyerhof公式误差最大，Vesic公式误差最小；当φ＜25°、粘聚力c＜20 kPa时，各公式预测误差一般不超过10%；各公式预测误差随地基土内摩擦角和粘聚力增大而增大。

极限承载力；载荷试验；三维有限元

0 引言

自Rankine首次提出地基极限承载力计算公式后，Prandtl、Reissner、Terzaghi、Meyerhof、Hansen、Vesic等不断改进并发展了基于刚塑性理论的极限承载力计算方法，其中，广泛应用于实践的主要有Terzaghi、Meyerhof、Hansen和Vesic公式[1]。研究表明，地基极限承载力公式的影响因素包括基础埋深、基础宽度和形状、内摩擦角、粘聚力等[2-3]。在工程实践中，考虑到基础的形状、宽度和埋深等条件，这些方法之间所建议的各项承载力系数和承载力修正系数差别较大，使得即使在相同的条件下，不同公式经修正得到的极限承载力也会存在较大差别[4]。我国现行《建筑地基基础设计规范》[5]在确定地基承载力特征值时，一般采用理论公式计算值除以一个较大安全系数（一般取2～3）得到，总体上偏于保守。因此，对这些理论公式的可靠性和准确性的分析与比较仍然有待积累经验并深入研究。

为了研究Vesic、Hansen和Meyerhof这三个常用理论公式的适用性，了解其预测的准确性和可靠性，基于文献中平板载荷试验结果，结合有限元计算分析，对各理论公式预测粘性土地基极限承载力的准确性和可靠性进行了对比分析和评价，以期为工程中估算地基的极限承载力提供参考。

1 表达形式与参数

Meyerhof、Hansen以及Vesic极限承载力理论计算公式的一般形式均可表示为：

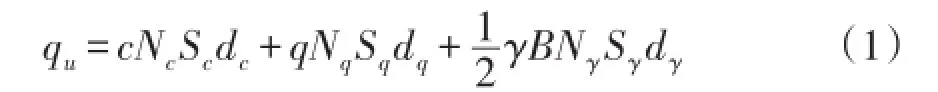
式中：c为地基土的粘聚力；q为基础底面以上超载；B为基础的宽度；Nc、Nq、Nγ为承载力系数；Sc、Sq、Sγ为形状系数；dc、dq、dγ为深度影响系数。

这三个理论公式间的区别主要是：（1）承载力系数的不同[7]，平面应变条件下，对土体的剪切破坏分析不同，Meyerhof分析了基础两侧有超载土体对抗剪强度以及摩擦作用的影响；Hansen在Meyerhof的基础上，又考虑了基础深基础和倾斜放置的情况；Vesic利用刚度指标对土体剪切破坏形式进行判别，指出不同剪切破坏形式下如何对承载力公式进行修正。（2）工程实践中，考虑到基础的形状、宽度和埋深等因素，在由平面应变推导出地基极限承载力公式的基础上，引入一定的参数修正，不同公式修正方法和系数计算间有差异。各公式系数差异详见表1（以方形基础为例）。

2 基础宽度和埋深的影响

选用文献[6]中的静载荷试验资料，用前述三种理论公式分别对粘性土地基相同基础埋深但不同基础宽度时极限承载力进行了预测，结果见表2。

表1 极限承载力系数和修正系数[8]Table 1 Ultimate bearing capacity coefficient and the correction coefficient

表2 静载荷试验资料及极限承载力计算结果与修正结果Table 2 Static load test data and the calculation and correction results of ultimate bearing capacity

可以看出，对于粘性土地基，载荷试验结果随基础宽度增大而迅速减小，这与“随基础宽度增大，承载力系数Nγ随之显著降低”[9]的研究结果相一致。然而，前述三个理论公式中承载力系数Nγ均没有反映基础宽度变化的影响（表1），其计算结果不随基础宽度而变化。当引入深度修正系数后，随着宽度增加，修正计算结果和试验结果的变化趋势一致，修正后Meyerhof公式的预测误差减小了20%，而Hansen公式则减小了10%。

利用文献[6]中的静载荷试验资料（表2），用前述三种理论公式分别对粘性土地基深基础（D＞B）和浅基础（D＜B）时极限承载力进行了预测，预测结果与试验结果对比见图1、图2。

由图1可以看出，Meyerhof公式和Hansen公式的预测结果数据点均位于45°线上方，即预测值均大于试验值。其中，Hansen公式最大预测误差超过载荷试验结果的50%。而Vesic公式不包含深度修正系数，不能反映不同埋深时承载力的变化。可见，对于粘性土深基础（D＞B），这三个理论公式均不适用。

类似地，由图2可以看出，这三个理论公式应用于浅基础极限承载力预测时，预测值也均大于实测值。其中，Vesic公式预测值误差最小，Hansen公式预测误差最大，最大误差未超过15%，远小于深基础情况。

可见，Meyerhof、Hansen以及Vesic极限承载力公式均不适用于粘性土深基础（D＞B），而对于粘性土浅基础（D＜B），三个公式的预测误差相对较小，可在一定的范围内使用。

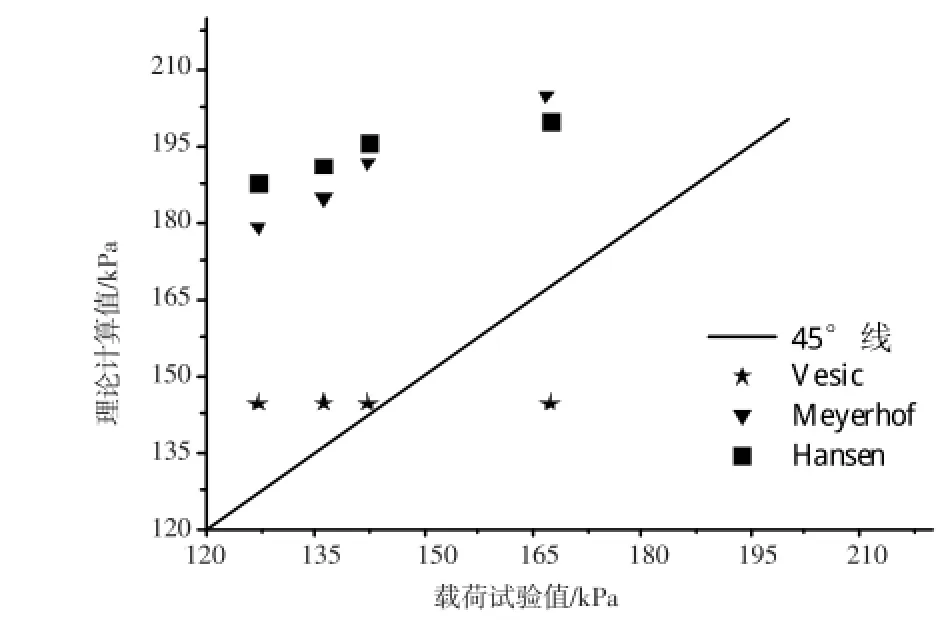
图1 载荷试验结果与计算结果比较（D＞B）Fig.1 Comparison of load test results and calculation results (D＞B)

图2 载荷试验结果与计算结果比较（D＜B）Fig.2 Comparison of load test results and calculation results (D＜B)

3 地基土参数影响

3.1 计算模型

由于能够收集到的详实的静载荷试验资料较少，为了研究不同条件下各理论公式的可靠性和适用性，采用ABAQUS进行粘性土浅基础三维有限元计算分析，以有限元计算结果为基准，分析比较各公式预测地基承载力的误差。

计算中考虑了无埋深基础（D=0.0 m）和有埋深浅基础（D=0.3 m）两种情况。考虑到对称性，取1/4基础和地基作为研究对象，其中基础尺寸为3.5 m× 3.5 m×3 m，地基土体的计算区域为50 m×50 m× 50 m。采用C3D8R八节点三维实体减缩积分单元，并对与基础接触部分区域的地基土进行网格细分（图3）。以地基沉降随基础顶部竖向荷载变化曲线上突变点来确定地基极限承载力大小。

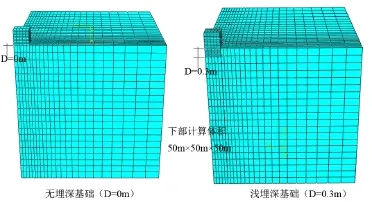
图3 无埋深和浅埋深基础FEM计算分析模型Fig.3 The FEA model of no buried depth and shallow foundation

3.2 计算参数选用

选取文献[6]中无埋深及有埋深浅基础各一组试验作为试算对象，当地基承载力的有限元计算结果与载荷试验相近，确定基础底面和侧面接触参数取硬摩擦，摩擦系数为0.27（tan 0.75φ，取φ=20°）。

试算结果表明，对无埋深基础（D=0 m，B= 0.71 m，c=9.8 kPa，φ=20°，γ=17.06 kN/m3），根据有限元计算结果绘制的lgP-S曲线（图4），确定极限承载力约为220 kPa，与实际载荷试验结果（220 kPa）一致。而对有埋深浅基础（D=0.3 m，B=0.71 m，c=9.8 kPa，φ=20°，γ=17.06 kN/m3），由有限元结果绘制lgP-S曲线（图4）确定的极限承载力约为240 kPa，略小于实际载荷试验结果（257 kPa）。

图4 无埋深与有埋深浅基础沉降lgP-S曲线Fig.4 The settlement lgP-S curve of no buried depth and shallow foundation

从上述试算结果可以看出，建立的有限元模型及选用的接触参数能够较准确地反映基础与地基的相互作用，下文将以该模型及接触参数在不同土性条件下的有限元计算结果为基准，来比较分析不同地基承载力理论公式的预测能力及预测误差。

3.3 地基粘性土内摩擦角的影响

分别用上述有限元模型和理论公式计算了有无埋深时地基土的内摩擦角为5°、10°、15°、20°、25°和30°时的地基承载力，将数值计算结果与理论公式计算结果对比绘制于图5、图6中。

从图5可以看出，对无埋深基础地基，当φ＜25°时，有限元和理论公式计算的地基承载力大小基本上一致，二者的结果较为吻合。随着摩擦角的增大，理论计算值与有限元计算值相对误差增大；当摩擦角φ达到30°时，理论公式的地基承载力计算结果比有限元计算结果大约13%。

图5 地基土内摩擦角变化时有限元计算值与理论公式计算值比较（无埋深基础）Fig.5 Comparison of FEA calculation values and theoretical formula calculation values with the variation of internal friction angle of foundation soil(no buried depth foundation)

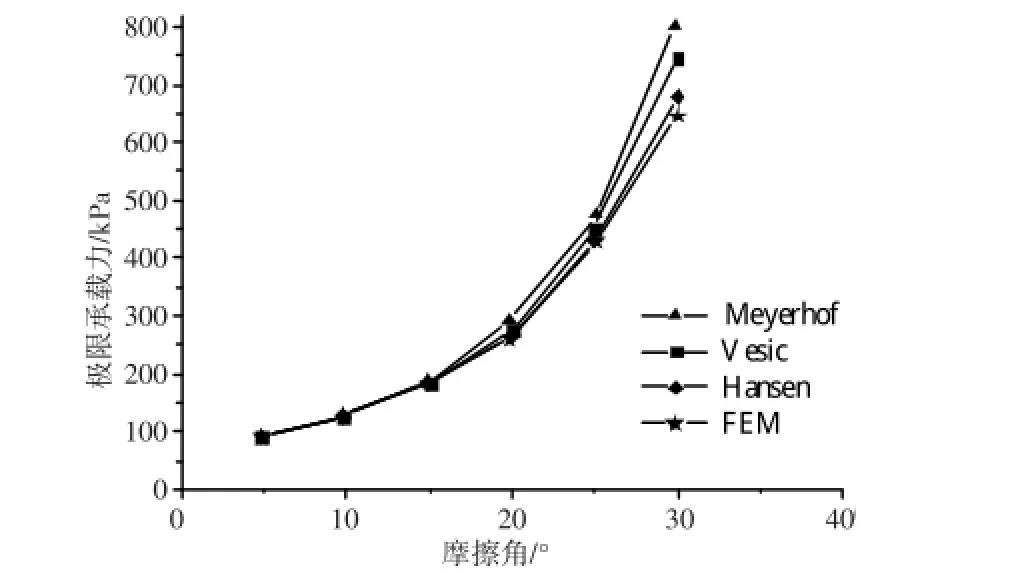
图6 地基土内摩擦角变化时有限元计算值与理论公式计算值比较（有埋深浅基础）Fig.6 Comparison of FEA calculation values and theoretical formula calculation values with the variation of internal friction angle of foundation soil(shallow foundation)

从图6可以看出，对有埋深浅基础地基，随着摩擦角的增大，理论公式计算结果与有限元计算结果误差也不断增大。当φ=30°时，Meyerhof和Han⁃sen公式的计算结果比有限元计算结果大25%以上，其误差是无埋深基础计算时的2倍；此时Vesic公式的计算结果和有限元计算结果基本一致，相对误差约为5%。而当φ＜20°时，理论公式计算结果与无埋深条件下结果相似，理论结果与有限元结果相对误差较小，所得结果比较可靠。

3.4 地基土粘聚力的影响

利用上述有限元模型和理论公式计算了有无埋深时地基土的粘聚力为5 kPa、9.8 kPa、15 kPa、20 kPa、25 kPa和30 kPa时的地基承载力，将数值计算结果与理论公式计算结果对比，见图7、图8。

图7 地基土粘聚力变化时有限元计算值与理论公式计算值比较（无埋深浅基础）Fig.7 Comparison of FEA calculation values and theoretical formula calculation values with the variation of cohesive force of foundation soil(no buried depth foundation)

图8 地基土粘聚力变化时有限元计算值与理论公式计算值比较（有埋深浅基础）Fig.8 Comparison of FEA calculation values and theoretical formula calculation values with the variation of cohesive force of foundation soil(shallow foundation)

从图7可以看出，对无埋深基础地基，当c＜20 kPa时，有限元和理论公式的计算结果基本上一致，理论公式计算所得结果较为可靠；而当c＞20 kPa时，理论公式的计算值与有限元计算结果之间的相对误差随着粘聚力的增大而逐渐偏大，粘聚力c达到30 kPa时，理论公式的计算结果比有限元计算结果大约20%。

从图8可以看出，对有埋深浅基础地基，随着粘聚力的增大，理论公式计算结果与有限元计算结果的相对误差不断增大，且误差明显大于无埋深基础地基。当粘聚力c达到30 kPa时，Meyerhof、Han⁃sen、Vesic公式计算结果比有限元计算结果依次偏大40%、25%、10%。当c＜30 kPa时，Vesic公式的计算结果与有限元计算结果相对误差较其他两个公式误差小，有埋深的情况下需要利用理论公式计算地基承载力时建议使用Vesic公式。

4 结语

通过采用文献中一些载荷试验的试验数据和计算数据，采用ABAQUS弹塑性有限元分析研究了不同的地基极限承载力公式的可靠性和适用范围。通过分析得出以下结论：

（1）三个公式预测粘性土地基浅基础（D＜B）极限承载力误差相对较小，在极限荷载不高于500 kPa时，相对误差不超过12%，计算得到的安全系数在规定范围内；但对于粘性土深基础（D＞B），即使在较小荷载时，计算所得的地基承载力误差大小一般都在30%以上，三个公式均不宜使用。

（2）对于粘性土浅基础，三个公式预测值总体上均偏大，一般Meyerhof公式误差最大，Vesic公式误差最小。当φ＜25°、粘聚力c＜20 kPa时，对于无埋深条件，各公式预测误差一般不超过10%；各公式预测误差随地基土内摩擦角和粘聚力增大而增大。 ■

[1]钱家欢,殷宗泽.土工原理与计算[M].北京：中国水利水电出版社，1996.

[2]De Beer.Experimental determination of the shape factors and the bearing capacity factors of sand[J].Geo-technique, 1970,20(4):387-411.

[3]Chen W F.Limit analysis and soil plasticity[M].Amster⁃dam:Elsevier Scientific Publishing Company,1975.

[4]廖化荣,赵宇鷃,王占华.地基极限承载力确定方法的分析与评价[J].中山大学研究生学刊(自然科学、医学版), 2005(2)：140-143.

[5]GB 50007-2002，建筑地基基础设计规范[S].

[6]Bowles J E.基础工程分析与设计[M].唐念慈，译.北京：中国建筑工业出版社,1987.

[7]Ukritchon B.Calculations of bearing capacity factor Nγusing numericallimitanalyses[J].JournalofGeotechnicalandGeoenvironmentalEngineering,ASCE,2003,129(6):468-474.

[8]蒋益平,熊巨华.方形和圆形基础地基极限承载力分析[J].岩土力学,2005,26(12):1991-1995.

[9]杜佐龙,黄茂松,秦会来.基底宽度对承载力系数Nγ的影响分析[J].岩土工程学报，2010,32(3)：408-414.

[10]GB 50330-2002，建筑边坡工程技术规范[S].

作者邮箱：XDBSK@163.com

Comparison of ultimate bearing capacity prediction for cohesive soil foundation with 3 theoretical

formulas

BAO Song-kao,WANG Qi-gui and YANG Mei-ping

Wenzhou Oujiangkou Development

and Construction Investment Group Co.,Ltd.

Based on the cited data of loading tests and calculation,3-D finite element analysis is con⁃ducted with the software ABAQUS.Comparison of 3 theoretical prediction formulas for ultimate bearing capacity is carried out,which are Vesic's,Hansen's and Meyerhof's.This paper discusses the impact on prediction results of foundation size,foundation embedded depth and soil properties.The results show that:(1)The prediction errors of these three formulas are relatively low when they are used for shallow foundation(D＜B)of cohesive soils.However,none of these three formulas is applicable for deep founda⁃tion(D＞B)of cohesive soils.(2)For shallow foundation of cohesive soils,the ultimate bearing capacity is totally overestimated with these three formulas.In general,prediction result of Meyerhof's formula is largest,and Vesic's is closest;when the soils'properties meet the condition of φ＜25°and c＜20 kPa,the prediction errors of these formulas are no more than 10%generally;the prediction errors of these formu⁃las increase with the increasing of the frictional angle and cohesion of foundation soils.

ultimate bearing capacity;loading test;3-D finite element analysis

TV223

A

1671-1092（2015）04-0020-05

2015-05-04

包松考（1973-），男，浙江泰顺人，工程师，主要从事市政工程管理。