我国近十年美术教育研究热点知识图谱
2015-01-16赵诚程
赵诚程
(温州大学 浙江温州 325030)
我国近十年美术教育研究热点知识图谱
赵诚程
(温州大学 浙江温州 325030)
借助Bicomb软件及SPSS软件对近十年国内美术教育的研究热点进行分析,结果表明美术教育的研究热点可以从两个维度和四个热点分类展开,两个维度:学校美术教育和美术教育对于发展创造力的研究,四个热点分类:美术教育的课程设置及开发儿童创造性思维的研究,儿童在美术教育中的体验性研究,学校美术教育,当代艺术及教学模式的研究
美术教育 关键词 知识图谱
1 引言
美术教育是人类重要的文化教育活动。它适应于人们延续美术文化,传播社会知识,表达内心情感,满足审美需求的愿望而产生,并随着人类的进步和社会的发展而日趋成熟。作为一种重要的教育门类,美术教育以其独特的方式发展和完善了人的精神和身体,促进了人类文明程度的提高,同事,其自身也在这一过程中得以完善和发展。美术教育与人类及其社会形成了彼此助益,双向建构的关系。
19世纪以来,美术教育在西方发达国家出现并迅速发展起来。作为美术教育发源地的德国,19世纪开始就比较重视美术对人的素质的影响,它将美术教育视为一种文化哲学的应用学科,其目的在于纠正科学理性主义给社会以及人本带来的负面效应,以完善人格,表达个性,陶冶情操,提高民众的审美趣味;而美国的美术教育从一开始带有浓重的实用主义色彩,其目标是为蓬勃发展的资本主义经济培养有一定技艺的劳动者。同时,也帮助人们从美的角度选择日常生活用品和服饰,美化环境,欣赏和评价各类美术作品,并发展每个人的创造能力。自20世纪50年代后期开始,我国也开始注重审美教育的培养,教育部几易课标,直到2001年颁布了较为适合我国国情的《全日制义务教育美术课程标准(实验稿)》,并提出课程的基本理念:使学生形成基本的美术素养;激发学生学习美术的兴趣,引导学生在文化情境中认识美术;培养创新精神和解决问题的能力。这才相对比较完善的将美术教育作为真正的学科较为全面的推广到社会中去。但是,由于考试机制的存在,美术教育在学校教育的实施过程中并不能够更全面的展开并发挥作用,因此创造力就不能更好的去培养,加之艺术教育相对于文化课教育,本来就不被重视,很多学习美术出来的学生原本就是奔着通过学习艺术而上学,毕业后虽然找到相关工作但却不能很投入的热爱,因此导致了师资的匮乏,在某种角度上造成了恶性循环。
尽管如此,随着全球化以及社会观念的慢慢变化,人们会转变学习艺术的角度意识,美术教育也会逐渐走向新的领域和层面,变成不仅仅是艺术的教育,更是贯穿于整个教育体系中的教育链接,本文就是通过对近年来更多老师和学者对美术教育的研究进行小部分的综合分析,探索,总结得出近几年美术教育的研究趋势及热点问题并进行讨论,从而更好的判断接下来的美术教育的研究及发展趋势。
2 资料来源与研究方法
2.1 资料来源
2.2 研究工具
主要研究工具有Bicomb共词分析软件、SPSS13.0和SPSS20.0。其中Bicomb共词分析软件由中国医科大学医学信息学系崔雷教授和沈阳市弘盛计算机技术有限公司开发。首先使用Bicomb共词分析软件对研究资料进行关键词提取,获得高频关键词的共现矩阵;其次,使用SPSS13.0获得高频关键词的相似矩阵;最后,使用SPSS20.0进行聚类分析和多维尺度分析。
2.3 研究进程
首先,将从CNKI检索到的343篇有效文献导出,存为文本文档,并将文本格式存为Bicomb软件能够识别的ANSI编码格式;其次,在Bicomb软件中建立新项目,将文本文档导入,提取文献中的关键词字段,统计得到472个关键词,选择词频大于等于6的19个高频关键词生成共现矩阵,导出矩阵到文本文档中;第三,将共现矩阵导入到SPSS13.0中,得到高频关键词的相似矩阵,并在excel中通过运算(1-相似矩阵)得到高频关键词的相异矩阵;第四,在SPSS20.0中运用共现矩阵进行聚类分析,得到关键词聚类树图;第五,在SPSS20.0运用相异矩阵进行多维尺度分析,绘制出科学课程研究热点知识图谱;最后,结合关键词聚类树图和研究热点知识图谱进行解释和分析。
3 研究结果与分析
3.1 高频关键词及分析
通过对233篇有效文献进行关键词统计并抽取词频大于等于4的34个高频关键词,结果如表1。通过对高频关键词的统计分析,可以更直观地把握研究领域的集中热点和趋势。
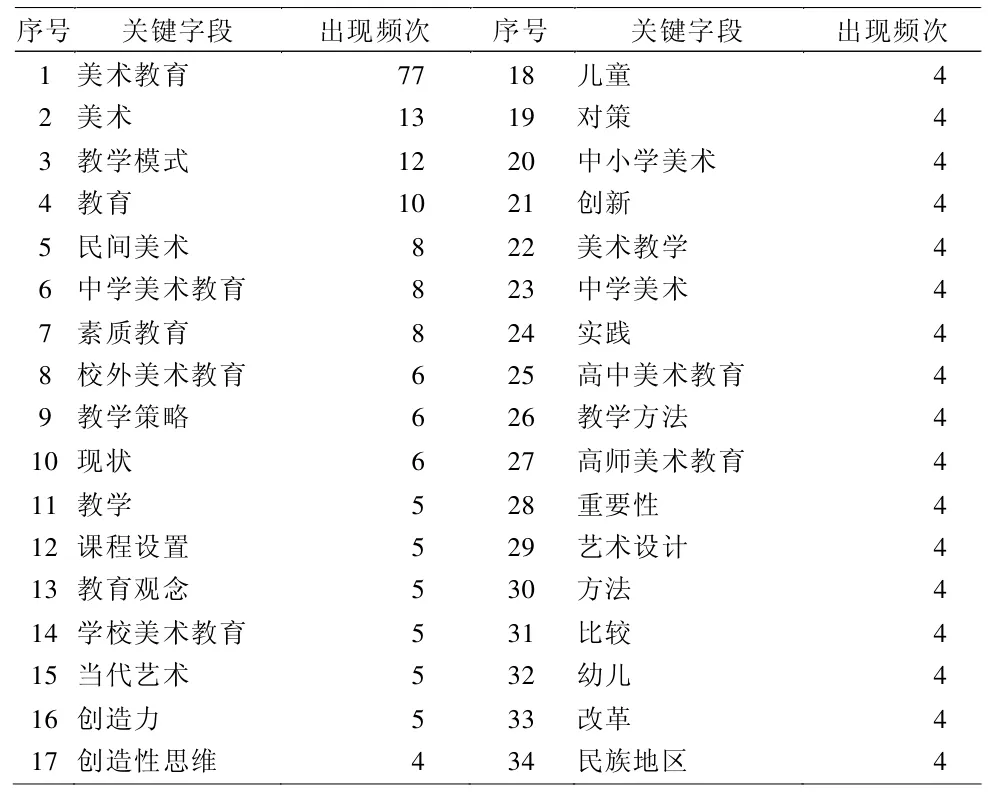
表1 前19位高频关键词排序
从表1可以初步地了解到近十年来我国美术教育课程领域的集中热点和趋势。具体为,前10个热点分别为:美术教育(77)、美术(13)、教学模式(12)、教育(10)、民间美术(8)、中学美术教育(8)、素质教育(8)、校外美术教育(6)、教学策略(6)、现状(6)。但是,仅通过统计分析高频关键词的词频难以发现关键词间的联系,因此,需要通过关键词共现技术来进一步挖掘它们之间的联系。
3.2 高频关键词的Ochiai系数相异矩阵
为了得到符合尺度分析要求的数据结构,应用Bicomb软件对上述19个高频关键词进行共词分析,生产共现矩阵,将共现矩阵导入SPSS13.0,生成共词相似矩阵,再在Excel中转化为相异矩阵,结果见表2.
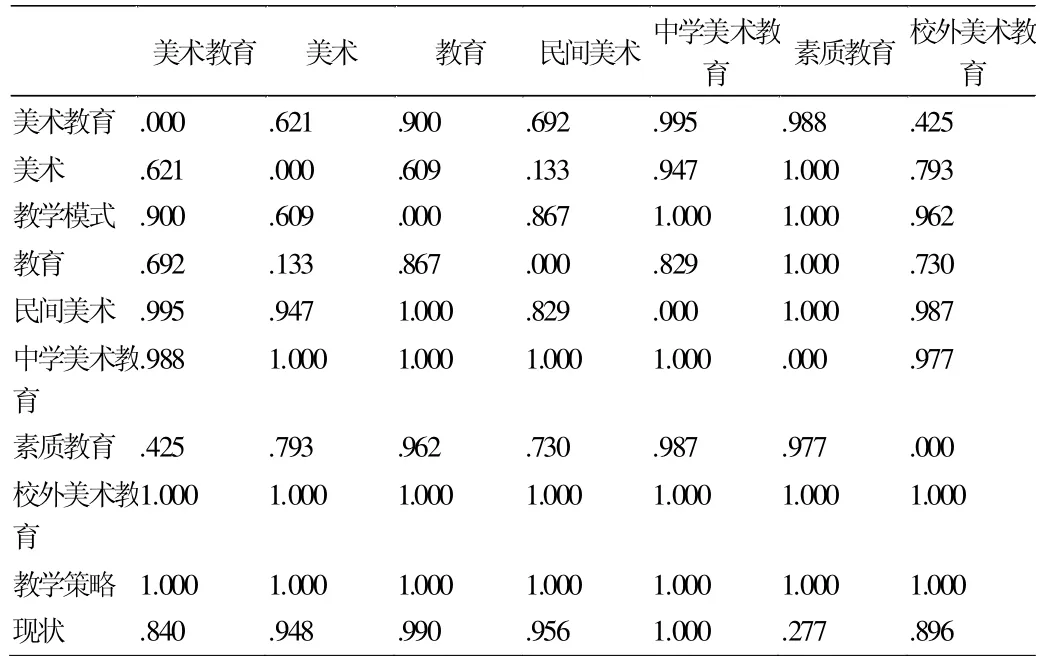
表2 高频关键词Ochiai系数相异矩阵(部分)
表2相异矩阵中的数字表示数据间的相异性,即对应的两个关键词距离的远近。数值越大则关键词间的距离越远,相似度越低;而数值越接近零,则表示关键词间距离越近,相似度越高。下面将通过对知识图谱的分析清晰展现其研究现状。
3.3 高频关键词聚类分析
聚类图显示出关键词之间关系的亲疏远近,进一步反应科学课程的研究热点分布规律。关键词聚类分析是以关键词两两之间同时在一篇文章中出现的频率(共词)为分析对象,利用统计学方法,将关联紧密的关键词聚集成类团。先以最有影响力的关键词(种子关键词)生成聚类;然后,由聚类中的种子关键词及相邻的关键词再组成新的聚类。关键词之间越相似,他们的距离则越近;反之,则越远。使用SPSS20.0对关键词的相异矩阵进行系统逐次聚类分析,生成的聚类结果见图1.
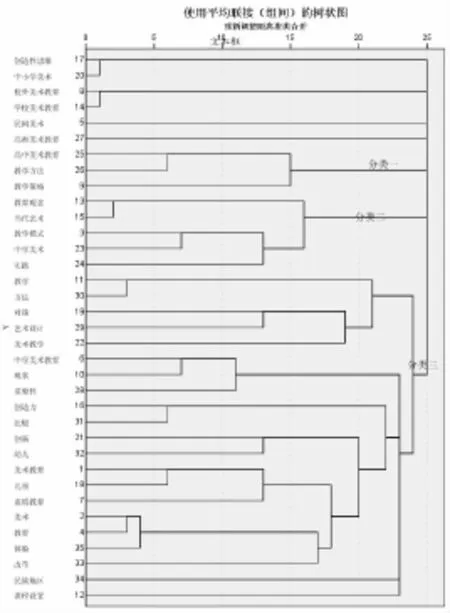
图1 美术教育研究领域关键词聚类图
根据图1的聚类分析的连线,可以将美术教育研究领域分为三大类。分类一是对美术教育的学校教育及其创造力培养的研究,包括创造性思维,中小学美术,校外美术教育,学校美术教育,民间美术,高师美术教育,高中美术教育,教学方法,教学策略9个关键词;分类二是对教育观念和教学模式的研究,包括教育观念,当代艺术,教学模式,中学美术,实践5个关键词;分类三是对中小学美术教育课程的研究,包括艺术设计,幼儿,美术教育,美术,体验,改革等21个关键词。
3.4 美术教育研究热点知识图谱及分析
利用SPSS20.0对相异矩阵进行分析,得到知识图谱,再结合聚类分析的结果对图上的研究热点进行划分,见图2.
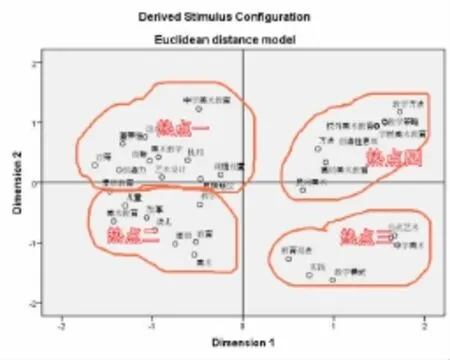
图2 2004-2013年我国美术教育研究热点知识图谱
图2 的结果以更直观的形式,更明晰的向我们展示了美术教育研究的热点问题,进一步向我们展示了美术教育研究主要围绕学校美术教育,教育方法和课程设置的问题进行展开,它们分别为:美术教育的的设置对于培养创造力的研究,美术教育体验教学的研究,当代艺术对美术教学观念影响的研究,从图2中4个具体研究领域的分布情况看,我国科学课程研究大部分还停留在对美术课程设置方面的研究,对于当代艺术以及儿童绘画体验模式的教学较少。
4 结论与展望
综上所述,知识图谱法比较直观的反映了我国近9年的美术教育的研究主要围绕美术课程模式,教学方法以创造力的培养方面,主要研究领域为中小学美术课程的研究,美术体验教学的研究,美术教学的策略方面。
通过对聚类分析图和多为尺度分析图的进一步归纳分析,我们可以看到,近9年国内关于美术教育研究相对较为丰富,但也存在着以下问题:(1)研究缺乏系统性和连续性。很多成果都停留在对其内涵、概念、模式等的解读,或是对国外有关文献的介绍,很多都是泛泛而谈,没有形成体系;许多论文大同小异,选题缺乏创新性,研究缺乏深度;很多研究只是短期内对某一问题的关注,缺乏长期连续的研究。这些研究基本上是局部性的,处于各自为战的散乱状态,缺乏宏观上的把握和协调。处于这种状态下的研究往往是粗浅的、片面的。(2)许多边缘化的问题没有被延伸,拓展,比如,民间美术教育,当代艺术,以及教学模式问题,这些都没有很好的进行延伸。如果将这几个因素进行延伸,或许对前面的几项研究会更加有帮助。
综上所述,美术教育研究仍然有很大的空间供研究者发掘,我们希望能够通过知识图谱为后继研究者提供参考,期待更多的研究者参与到科学课程的研究中,为将来美育在我国的实施提供充足的理论支持。
赵诚程(1989.2~)女 籍贯山东淄博 单位 温州大学2012级美术课程与教学论研究生 研究方向:儿童美术教育
找资料。打开中国知网,进入中国学术期刊
总库,以“美术教育”和“美术教学”为主题词,将来源类别限定为“核心期刊”,开始检索2004—2013年相关文献,得到343篇相关文献。其次,确定研究资料。本文的研究范围限定在中小学教育和美术教育的课程设置的相关内容的研究,因此剔除了与本文研究范围不相关的文献,并剔除会议通知、书评、人物介绍以及没有关键词、重复发表的文献等,最后得到有效文献233篇作为研究资料。最后,规范资料。使资料的编码格式符合研究工具要求,并标准化关键词使其含义保持一致。
