方腔内合金相变材料的熔化过程*

郭茶秀，陈 俊

（郑州大学 化工与能源学院，郑州 450001）

方腔内合金相变材料的熔化过程*

郭茶秀†，陈 俊

（郑州大学 化工与能源学院，郑州 450001）

本文利用CFD软件对方腔内合金相变材料在温差作用下的熔化过程进行了数值模拟研究。通过与试验结果的比较，验证了本文采用的模型和算法的正确性。同时，详细研究了熔化过程中合金相变材料的固−液界面、温度及环流速度的变化规律。结果表明，为了减小传热热阻，加快合金的熔化速度，从方腔的侧面和底面加热相变材料时熔化效果最好。

合金相变材料；熔化；数值模拟

0 引 言

工贸企业存在大量的低品位工业余热，由于工业余热的不连续性，使得现有以直接回收利用为主的余热回收技术无法实现低温的余热跨时间、空间梯级利用，从而导致企业能源综合利用率较低。而储能技术能解决能量供求在时间和空间上分配的不均匀性，可有效提高能源利用率，在工业的热过程、新能源利用、民用建筑采暖等方面已得到广泛应用[1]。

目前的热能存储技术主要包括显热、潜热和化学储热三种。其中潜热存储以其储热密度高、温度变化小、容易控制等特点，成为合理利用能源、减小环境污染、提高能源利用率的一种储能方式[2]。潜热存储所使用的相变材料分为有机、无机和混合相变材料三类，其中Ga、Pb等合金，因具有储能密度大、热循环稳定性好、导热系数大、过冷度小等特点而受到国内外研究者的关注，并且主要在合金的热物理性能研究方面取得了一定的进展[3]， 但在其传热性能方面研究较少，因此在合金的传热方面还可以开展许多研究。

在合金相变材料相变过程中，由温差引起的自然对流始终存在，使得合金相变材料熔化或凝固时固−液界面的位置受时间、温度、传热量以及容器形状尺寸等因素的影响，极大地增加了研究固−液界面运动规律和传热效率的复杂性。本文利用CFD软件FLUENT[4]对合金相变材料在自然对流条件下的相变过程进行了数值模拟研究，探讨了其相变过程中自然对流对温度分布、环流速度及固−液界面随时间的影响，为相变材料的有效利用、蓄热系统的优化设计及性能的准确分析提供参考依据。

1 物理模型及数学模型的建立

1.1 物理模型

本文研究的物理模型[5]如图1所示，方腔内装入合金镓作为相变材料，其热物性如表1所示。方腔的尺寸为：x方向长8.89 cm，y方向长6.35 cm，z方向远大于x、y方向。上下两面设有保温层，左右两侧面温度恒定，相变材料的相变温度在两者之间以便于模拟计算。左侧面为加热面，温度为38℃；右侧面温度为28.3℃。为了分析方便，可将其物理模型简化为x、y平面内的二维模型，并做了以下假设[6]：

（1）流体中粘性耗散不计；（2）除密度外其他物性为常数；（3）自然对流是由液相的密度发生变化而形成的，而密度变化符合Boussinesq假设。

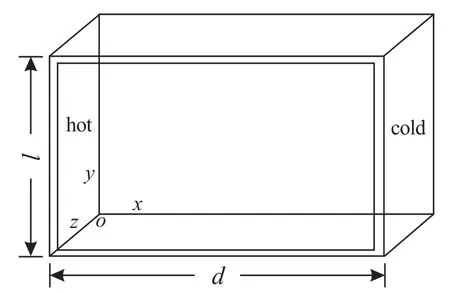
图1 物理模型Fig. 1 Physical model

表1 相变材料热物性参数Table 1 property parameters of PCM

1.2 数学模型

由于合金相变材料相变过程是一个非稳态过程，且相变过程中传热方式以导热和对流为主，比单纯的导热或者单纯的对流情况复杂得多。尤其是因为相变传热是一个非线性的传热问题，叠加原理不再适合。因此在求解能量方程的过程中引入焓，并将整个相变区域看成多孔介质，孔隙度用液相分数lf来表示，当lf=0时，模拟对象为固相，流体的流速为0；当lf=1时，模拟对象为液相，流体的流速为动量方程的速度；当0＜lf＜1时，模拟对象为模糊区，流速为液相分数的函数。考虑到自然对流的影响，在连续方程中应考虑到密度的变化，在动量方程中应该考虑体积力的影响，故其二维控制方程及边界条件如下：

连续方程：

动量方程：

能量方程：

基于前面的假设，动量方程中的密度表示为：

动量方程的源项：

能量方程源项：

式（6）中ε是一小于0.000 1的数，Amush为糊状区域的连续数（在104～107之间）。

能量基本方程式（4）中的H表示为：

自然对流是在重力场或者其他力场的作用下由密度差引起的浮升力产生的，大多数情况下，密度差是由于温度差引起的，液体受热或冷却后体积膨胀或缩小，导致密度增大或减小。假设远离加热面某点处的液体密度为ρ'，加热面附近某点处液体的密度为ρ，则ρ=ρ'(1-βΔT)，于是这两点将形成压差：

当Δt较小时，，在压差的推动下，必然造成液体的环流，其速度满足关系式：

式中，β为体积膨胀系数，ΔT为两点的温差，l为受热面的高度，g为重力加速度，u为速度绝对值，ρ为密度，p为压力。

可见环流速度的绝对值取决于流体的性质（例如粘度）、流动空间的几何形状及尺寸。

2 模拟过程的实现及结果

2.1 参数设置

利用Gambit 2.1.3对图1所示简化后的2D计算模型进行网格划分，经过网格独立性考核，网格总数选为1 344个。将网格文件导入FLUENT 6.3中，定义求解器Solver为分离式2D，非稳态，一阶隐式；选定Solidification/Melting模型；输入相变材料热物性参数及边界条件；离散项中压力梯度项采用PRESTO格式，压力速度耦合项采用SIMPLE算法；时间步长取0.1 s。为了得到相变过程中温度与速度的关系，在计算模型中设置了水平线y=3.175上的4点：point1、point2、point3、point4。4个点的横坐标为x=1.778 cm、x=3.556 cm、x=5.334 cm、x=7.112 cm，并监视这4个点的温度、速度与时间的关系。另外，为了获得各个时刻系统中温度的分布情况，定义了平行于x轴的4条直线，这4条直线的纵坐标为y=1.27 cm、y=2.54 cm、y=3.81 cm、y=5.08 cm[5]。

2.2 模拟结果及分析

图2所示为模拟计算结果，与文献[7]的试验结果相比较，证明本文模拟的结果是正确的。

图2 计算与实验结果的比较Fig. 2 Comparison of simulation and experimental results

为了分析蓄热温差ΔT=Thot-T（cTc为相变材料的熔点）为10℃时自然对流对相变过程的影响规律，将初始温度设为相变材料的熔点。图3所示为ΔT=10℃，计算模型中相变材料的固−液界面在不同时刻的固−液界面分布情况。

图3 相变材料固−液界面Fig. 3 Interface of solid-liquid in PCM

从图3可以看出，在熔化的初始阶段，由于相变材料的液态量较少，传热的方式主要以导热为主，2 min以前方腔内的界面曲线弯曲不大，但是随着时间的推移，固−液界面弯曲越来越严重。由于液态量逐渐增多，导热方式从以导热为主转变成以对流为主，靠近加热壁面的液相相变材料由于温度升高，密度减小，在浮力的作用下向上移动，方腔的上部受到热流的冲击，使得上半部分相变材料熔化的速度加快，同时由于热的相变材料在与固−液界面发生对流换热后，液态的温度降低，使得液态相变材料在靠近固−液界面区域向下流动，产生回流。由于沿固−液界面回流时液态温度逐渐降低，故使得固−液界面的移动速度沿自身自上而下逐渐减小。

图4 和图5为自然对流条件下，相变材料分别在5 min、15 min时刻的相变过程中的等温线图。从不同时刻等温线来看，受自然对流的影响，在液相区（温度大于302.93 K）有两个区域的温度梯度较大，一个是位于方腔上部的固−液界面前沿，此区域是由于受到热流体的冲击；另一个区域是位于方框下方靠近加热壁的区域，此区域是由于冷流体回流后被加热。受自然对流的影响，一方面，液体加热后温度升高，密度减小，在浮力的作用下向上流动，加热面附近的液态相变材料的温度迅速升高并沿加热面上升；另一方面，在固−液界面附近的相变材料，由于不断地向固−液界面传递热量，温度不断降低并导致密度增大，逐渐下沉。高温流体在上升过程中与固−液界面接触时，由于两者的温差较大（固−液界面的温度始终等于相变温度），使得该区域的温度梯度较大；同样低温流体下降冷却后与加热面接触时，由于加热面的温度远高于流体的温度，使得该区域的温度梯度也较大。低温流体加热后上升，高温流体传递热量后下降，从而导致液态的循环流动。因此，可以推测从侧面和底面加热时，固态能够始终与加热面相接触，熔化速度最快，效果最好。

图4 相变材料在5 min时的等温线Fig. 4 Isothermal line at 5 minutes in PCM

图5 相变材料在15 min时刻的等温线Fig. 5 Isothermal line at 15 minutes in PCM

图6为=ΔT10℃条件下，本文所设置的4点温度随时间的变化图。由图6可看出，未达相变温度之前，各点温度逐渐升高，距离加热面越近，曲线斜率越大，温度升高越快；当温度达到相变温度之后，各点的温度发生波动，波动先增大后减小，且温度始终不低于相变温度。温度未达相变温度之前，相变材料为固态，热量以导热的形式传递，离加热面越近，热阻越小，温度上升越快，此阶段以显热的形式储存热量；当温度到达相变温度之后，受液态自然对流的影响，该点温度产生波动，此阶段以潜热的形式储存热量；当相变完成后，自然对流引起的循环流动使流体区域的温度均匀化，随着蓄热的进行，温度波动逐渐减小并逐渐升高，此阶段又以显热的形式储存热量。在不考虑自然对流的条件下，各点的温度均不会发生波动[8]。

图6 四点温度随时间的变化Fig. 6 Temperature changes with time at four points

图7～图10分别为y=1.27、2.54、3.81、5.08 cm四条直线上，合金相变材料在2、4、6、8、10、12、14、16 min时的温度分布图。从图中可以看出在2 min的时候，相变材料在相变的初始阶段，由于液相量比较少，各等高线上的温度在熔点以上呈直线分布；4 min的时候，由于热流体向上流动，y=1.27 cm和y=2.54 cm 的温度仍呈线性分布，而y=3.81 cm和y=5.08 cm的温度分布线发生了扭曲，并随时间逐渐加强；16 min的时候，在x=0.01 m到x=0.08 m的中间部分，直线y=5.08 cm的温度分布比较平稳、温度最高，y=3.82 cm和y=2.54 cm次之，y=1.27 cm最陡。蓄热过程中，液态相变材料加热后不断上升，并尽量靠近上壁面流动，温度越高，上升越高，使同一水平面上的温度均匀化。由以上可知：在无限接近上底面的等高线上，温度分布最平稳，最接近加热面的温度。合金相变材料在相变过程中受自然对流的影响，液态区域的传热以对流为主，液态受热之后密度减小，在浮升力的作用下迅速离开原来的位置，使得热量尽量传递到温度较低区域，导致固态熔化速度加快。

图7 y=1.27 cm温度随时间分布Fig. 7 Temperature distributions at liney=1.27 cm

图8 y=2.54 cm温度随时间分布Fig. 8 Temperature distributions at liney=2.54 cm

图9y=3.81 cm温度随时间分布Fig. 9 Temperature distributions at liney=3.81 cm

图11所示分别为point1、point2、point3、point4四点的速度随时间的变化规律。结合图7可以看出：相变材料在未达熔点之前，各点速度为零。当温度超过熔点以后，由于对流产生速度的影响，各点的温度在熔点以上发生波动。同时由于环流的流速与温差成正比，各点的速度随温度波动增大而增大，到达最大之后逐渐减小。随着温差波动的减小，各点速度逐渐趋于零。

图10 y=5.08 cm温度随时间分布Fig. 10 Temperature distributions at liney=5.08 cm

图11 四点速度随时间的变化Fig. 11 Velocity changes with time at four points

图12为温差ΔT=10℃、15℃，相变时间为4 min时方腔内的相变材料的速度矢量分布图。从图中可以看出：在同一时刻，温差为15℃时相变材料的最大速率为2.36 cm/s，而温差为10℃时的最大速率为1.74 cm/s，即温差越大，相变材料的液相速率越大。在液相区，受自然对流的影响，液相环流随液相所占比例的增大而越来越明显，环流速度的绝对值除了取决于冷热面的温差外，还与流体的性质（如粘度、膨胀系数等）、流动空间的几何形状尺寸有关。

图12 速度矢量分布图（4 min时刻）Fig. 12 Velocity vector distributions at 4 minutes

3 结 论

（1）本文对自然对流作用下的合金相变材料镓的熔化过程建立了数学模型和物理模型，并利用FLUENT软件对其进行了数值模拟。通过与试验结果的比较，表明本文对合金相变材料的相变问题进行传热分析是正确的。

（2）合金相变材料在熔化过程中，由于浮升力的作用，热流体上升，冷流体下降，沿固−液界面回流时液态温度逐渐降低，故使其固−液界面的移动速度沿自身自上而下逐渐减小。在自然对流作用下，环流速度与温度差成正比。环流速度随温度波动增大而增大，到达最大之后逐渐减小，随着温差波动的减小，速度逐渐趋于零[5]。

（3）相变材料水平线的位置越高，温度分布越平稳，由此可推出无限接近上表面的水平线上，温度分布最平稳，最接近加热面的温度。

（4）根据对自然对流对合金相变材料熔化过程影响的分析，可知从方腔的两个侧面和底面加热相变材料时熔化效果最好，因为在相变材料熔化过程中固态下沉且更接近加热面，从而减小传热热阻，使熔化速度加快。

[1] Agyenim F, Hewitt N, Eames P, et al. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems, Renewable and sustainable energy reviews[J]. 2010, 14(2): 615-628.

[2] 张寅平, 胡汉平, 孔祥东. 相变贮能——理论和应用[M]. 中国科技大学出版社, 1996.

[3] 李元元, 程晓敏, 俞铁铭. Sn-Zn合金相变储热材料的热循环稳定性[J]. 特种铸造及有色金属, 2012, 32(7): 674-676.

[4] 韩占忠, 王敬, 兰小平. FLUENT流体工程仿真计算事例与应用[M]. 北京理工大学出版社, 2004.

[5] 陈俊. 相变蓄热技术的数值模拟研究[D]. 郑州: 郑州大学, 2007.

[6] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001.

[7] Gau C, Viskanta R. Melting and Solidification of a Pure Metal on a Vertical Wall[J]. ASME Journal of Heat Transfer, 1986, 108(1): 174-181.

[8] 周建辉. 高温固液相变蓄热器的结构设计和数值模拟[D]. 哈尔滨: 哈尔滨工程大学. 2004.

Phase Change Process of Alloy Phase Change Material in a Rectangular

GUO Cha-xiu, CHEN Jun
(School of Chemical and Energy Engineering, Zhengzhou University, Zhengzhou 450001, China)

The melting process of alloy phase change material in a rectangular under temperature difference is simulated by CFD software. The simulation model is verified by the experimental result. The impacts of the natural convection on the solid-liquid interface, the temperature and the circulation speed in the melting process are analyzed. The results show that the phase change material in rectangular should to be heated from the two sides and the bottom in order to reduce heat transfer resistance and get a faster melting speed.

alloy phase change material; melting; numerical simulation

TK02

A doi：10.3969/j.issn.2095-560X.2015.04.012

2095-560X（2015）04-0319-06

郭茶秀（1968-），女，博士，教授，主要从事新能源的开发与利用方面的研究。

2015-04-14

2015-05-28

国家自然科学基金（51176173）；河南省教育厅科学技术研究重点项目（14A480002）

† 通信作者：郭茶秀，E-mail：guochaxiu@163.com