葡萄酒理化指标质量评价数学模型

叶思平，陈海光，梁凯豪

(1.从化市职业技术学校，广州从化 510920；2.仲恺农业工程学院轻工食品学院，广东广州 510225；3．仲恺农业工程学院计算科学学院，广东广州 510225)

葡萄酒理化指标质量评价数学模型

叶思平1，陈海光2，梁凯豪3*

(1.从化市职业技术学校，广州从化 510920；2.仲恺农业工程学院轻工食品学院，广东广州 510225；3．仲恺农业工程学院计算科学学院，广东广州 510225)

葡萄酒质量是从葡萄酒的外观、香气和口感方面的综合评价，以往一般是通过评酒员来对葡萄酒的质量进行评估。通过研究葡萄酒的理化指标，包括花色苷、总酚和单宁等，对葡萄酒的质量进行评价。为了消除不同理化指标的量纲对葡萄酒质量评价值的影响，先要对葡萄酒的各个理化指标数据进行标准化，并根据离差最大化原理，建立葡萄酒质量的非线性规划(NLP)综合评价模型。结果表明，理化指标能够从一定程度上反映葡萄酒的质量。

MSE准则；葡萄酒；理化指标；NLP综合评价模型

当前，在对葡萄酒的质量进行评价时，多数分析方法是建立在评酒员感官评价的基础上的，但在实践中，由于各种因素的共同作用，如评价尺度的差异、评价位置的差异、评价方向的差异等，可能造成评酒员间出现异质性。如果能够通过测定葡萄酒中的理化指标，包括花色苷、单宁、总酚、酒总黄酮、白藜芦醇等，对理化指标进行综合评价，从而得到葡萄酒质量的评价，将会一定程度上减弱异质性。这种通过理化指标的方法可以有效地对评酒员间异质性问题进行检验。

1 葡萄酒理化指标分析

葡萄酒的理化指标主要有花色苷、单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积(IV50)、色泽和芳香物质总量。其中，色泽是通过颜色中的3个因素来测定的，分别为L*(D65)、a*(D65)、b*(D65)。

在红葡萄酒中，花色苷能起到辅助成色作用。所谓辅助成色作用[1]，即花色苷与葡萄酒中的辅色素如酚酸、类黄酮等作用，通过氢键形成一种三明治结构复合物，使葡萄酒色度更深、色泽更稳定。辅助成色作用能使花色苷产生红移效应，给葡萄酒带来一种更深的蓝色色调。除了感官上的作用，花色苷还能消除体内自由基及预防心脑血管疾病等生理作用[2]。因此，它是影响红葡萄酒质量的重要指标之一。

单宁是葡萄酒中所含有的一种酚化合物物质。单宁的多少可以决定酒的风味、结构与质地。缺乏单宁的红酒质地轻薄，没有厚实的感觉[3]；单宁丰富的红酒可以存放经年，并且逐渐酝酿出香醇细致的陈年风味。

葡萄酒中大量多酚化合物与抗氧化能力密切相关[4]。有学者从红葡萄酒中分离出多酚化合物，分离出的多酚化合物对人LDL的抗氧化能力比VE要高2倍左右。另外，还检测了20种加里福尼亚商业葡萄酒在体外对人LDL的抗氧化能力，结果显示，红葡萄酒的抗氧化能力为36%～65%，抗氧化能力与葡萄酒中总酚含量的相关系数为0.94。

黄酮类化合物具有降血脂、降血糖、增强人体免疫力的功能[5]。

白藜芦醇是红葡萄酒多酚物质的有效成分，各项研究证明，它具有抗血小板凝集、调节脂类代谢、松弛血管以及保护心脏和脑等功能[6]。

生物学上用DPPH法测量生物的自由基含量和对自由基的肃清才能即抗氧化剂的含量，自由基剩余量，称作半抑制量(半抑制体积)。

葡萄酒的颜色来源于葡萄中的色素，葡萄的色素则决定着红葡萄酒的颜色气质。红葡萄酒的颜色差别大，从黑紫色到各种红色都有，甚至会蜕变成琥珀色。红酒年轻时，颜色越深，酒的味道越浓郁，单宁含量也越高[7]。干白酒的颜色通常比较浅，年轻时常常带绿色反光，呈现出淡黄色，随着酒龄而逐渐加深。葡萄酒的颜色与其成熟程度也有密切关系，成熟度高的葡萄颜色越深；年份不好、葡萄成熟度不足，酒的颜色也会相应跟着变淡。

芳香物质是造就葡萄酒风味的物质之一，芳香物质越多，葡萄酒的风味就浓厚[8-9]。尽管芳香物质总量在葡萄酒的物质构成中所占比例非常小，但它们对葡萄酒的特色和风味有着非常显著的贡献。

从以上分析可以看出，虽然影响葡萄酒品质的因素很多，包括酿造技术和酿酒葡萄的产地、品质等，但是葡萄酒中的理化指标的含量起着非常重要的作用，可以用来作为判断葡萄酒质量的指标依据[10]。

2 葡萄酒NLP综合评价模型的建立

为了建立葡萄酒质量的综合评价模型，分别用Q1，Q2，…，Q10表示葡萄酒的10个理化指标：花色苷、单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积(IV50)、色泽(L*、a*、b*)和芳香物质总量，不妨设葡萄酒的评价体系L=(Q1，Q2，…，Q10)，并且取得了n个葡萄酒样品的10项理化指标的测量数据Qij(i=1，2，…，n;j=1,2,…，10)。下面的问题就是确定对应于Q1，Q2，…，Q10的权系数b1，b2，…，b10，求出葡萄酒的综合评价值Pi(i=1，2，…，n)，根据Pi的大小对葡萄酒的质量进行评价[11]。

为了尽可能反映实际情况，排除由于葡萄酒的各个理化指标不同量纲所带来的困难，以及各个理化指标数据大小悬殊对计算程度的影响[12]，可对以上葡萄酒10项理化指标的观测数据按如下方式进行标准化处理，即：

(1)

其中，

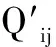
Pi=b1Qi1+b2Qi2+…+b10xi10，(i=1，2，…，n)

(2)

为了确定10项理化指标的权重系数b1，b2，…，b10，记b=(b1，b2，…，b10)T，并且按最大离差原理[15-16]，可以建立如下的非线性规划(NLP)数学模型：

(3)

模型(3)是一个带约束的非线性规划模型(NLP)，如果直接求解模型(3)的权重系数b=(b1，b2，…，b10)T是有一定困难的。因此，对模型(3)进行系列变换，以便于求出权重系数向量b=(b1，b2，…，b10)T。

不妨设P=(P1，P2，…，Pn)T，Q=(Qij)n×10，则评价葡萄酒质量的综合评价函数可以表示如下：

P=Qb

(4)

评价值变量P按n个葡萄酒样品取值构成的样本均方差为：

不妨设A=QTQ，并令μ=nσ2，则有：

μ=bTAb

由于bTb=1，于是非线性规划(NLP)模型(3)将变成如下形式：

(5)

s.t. A=QTQ

其中，b=(b1，b2，…，b10)T。

非线性规划(NLP)模型(5)的权重系数b=(b1，b2，…，b10)T可以根据下面的定理求解。

定理：方差μ=bTAb取得最大值时，b为对称正定矩阵A=QTQ的最大特征值λmax所对应的单位特征向量。换言之，NLP模型(5)的解b=(b1，b2，…，b10)T则为对称正定矩阵A=QTQ的最大特征值λmax所对应的单位特征向量[17]。

证明：设λ1，λ2，…，λ10为对称正定矩阵A=QTQ的特征根，不妨设λ1≥λ2…≥λ10，又设e1，e2，…，e10为A的正交化单位特征向量，则A的谱分解式为：

设a=(a1，a2，…，a10)，则：

这就证明了方差μ小于或等于对称正定矩阵A的最大特征值。然后采用Lagrange乘数法，设F(λ，b)=bTAb-λ(bTb-1)，式中λ为Lagrange乘数，则解必须满足下列条件：

于是，F(λ，b)=bTλb-λ(bTb-1)=λ。

要使F(λ，b)达到最大值，则应使λ达到最大值，而λ正是向量b所对应的特征根。因此，b为对称正定矩阵A=QTQ的最大特征值λmax所对应的单位特征向量。利用数值计算方法中的Jacobi法能快速求出矩阵A=QTQ的最大标准特征根以及对应的单位特征向量，即NLP模型的解b。

3 葡萄酒综合评价实证分析

这里，可以分别测量出27个红葡萄酒样品和28个白葡萄酒样品的10项理化指标数据。由于葡萄酒中芳香物质的种类繁多，以葡萄酒中芳香物质的总量作为葡萄酒芳香物质的衡量。

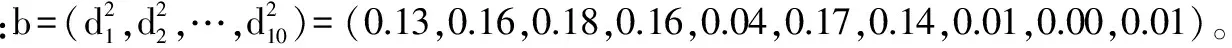
然后根据该权重系数和红葡萄酒10项理化指标的标准值，可以得出27种红葡萄酒样品的评价值。为了方便与评酒员对相应红葡萄酒样品的评分进行，将评价值扩大100倍。将红葡萄酒样品按照评酒员评分从小到大排序，并根据评分和评价值画图，得图1。

从图1中可以看出，评分曲线与评价值曲线的变化具有一定的一致性，两者的相关系数为0.866，这表明评价值能从一定程度上反映红葡萄酒的质量，大概能够反映出86.6%的红葡萄酒质量情况。

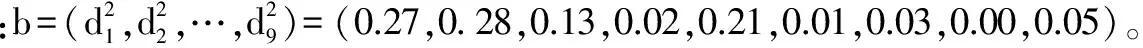
根据该权重系数算出28种白葡萄酒样品的评价值，同样将评价值放大100倍。将白葡萄酒样品按照评酒员评分从小到大排序，并根据评分和评价值可得图 2。

根据图2，评价值曲线基本上随着评分曲线的增大而增大，两者的相关系数为0.841，这表明评价值也能从一定程度上反映白葡萄酒的质量，大概能够反映出84.1%的白葡萄酒质量情况。

4 结论

理化指标对葡萄酒质量的影响，在不同品种的葡萄酒中有着不同的影响力。在红葡萄酒中，理化指标对红葡萄酒质量的影响为86.6%；在白葡萄酒中，理化指标对白葡萄酒质量的影响要低一些，为84.1%。因此可知，理化指标能在一定程度上反映葡萄酒的质量等级，但并不是葡萄酒质量评价的唯一基准。因为通过化学分析仪器测定得到的理化指标只能表示葡萄酒的化学成分含量．无法完全表示酒的风味质量和视觉感受。只有通过专业评酒员的目测、鼻嗅与口尝，才能依靠视觉、嗅觉、味觉对酒的色泽、芳香、滋味做出更加准确的鉴定。不过，利用该方法模型也可以对评酒员的异质性进行检验，减少评酒员个人主观误差的影响。

[1] 刘丽媛，苑伟，刘延琳．红葡萄酒中花色苷辅助成色作用的研究进展[J]．中国农业科学，2010，43(12)：2518-2526．

[2] 姚乾元．红葡萄酒保护心血管的功效[J]．食品与药品，2006，8(1)：72-73．

[3] 游玲，王涛，李华兰．葡萄酒芳香物质研究进展[J]．四川食品与发酵，2008，44(2)：29-33．

[4] 高尧来，温其标，张福艳．葡萄酒中的多酚类物质及其保健功能[J]．食品与发酵工业，2002，28(8)：68-72．

[5] 高山，胡平，龙世平．响应面法优化荸荠皮总黄酮的提取工艺[J]．化学与生物工程，2010，27(12)：41-44.

[6] 皱建凯.气相色谱/ 质谱研究中国干红葡萄酒香味成分[J].分析化学，2001，29(4)：492- 493．

[7] 房玉林，王华，张莉，等．不同酿造工艺对毛葡萄酒香气的影响[J]．农业工程学报，2007，23(2)：21-26．

[8] 马宗魁．葡萄酒香气分析[J]．酿酒，2009，36(2)：76-77.

[9] 李记明，宋长冰，贺普超．葡萄与葡萄酒芳香物质研究进展[J]．西北农业大学学报，1998，26(5)：105-109.

[10] 马腾,赵丽,李军.2008年份昌黎原产地葡萄酒理化特性的统计学分析[J].河北科技师范学院学报,2012(1):5-11,36.

[11] 梁凯豪，高凌云，梁海东．一类排序问题的求解及效果评估[J]．大学数学，2010，26(4)：157-161.

[12] 李文华．一类具有三重指标的分批排序问题[J]．工程数学学报，2007，24(1)：183-186.

[13] 梁雪春，谢岭南，陈森发，等．企业资信等级的定性定量评估模型研究[J]．东南大学学报：哲学社会科学版，2006，8(5)：31-34.

[14] JAN PIETER KRAHNEN，MARTIN WEBER.Generally accepted rating principles：A primer [J].Journal of Banking and Finance，2000，25(1)：5-6.

[15] 王应明．运用离差最大化方法进行多指标决策与排序[J]．系统工程与电子技术，1998，2(7)：24-31.

[16] XU Z S.Generalized chi square method for the estimation of weights [J].Journal of Optimization Theory and Applications，2000，107(1)：183-192.

[17] 成兰，郭瑞林．基于离差最大化原理的灰色综合评判方法及其应用[J]．数学的实践与认识，2007，37(20)：94-100.

[18] 张海妍，丁立孝，丁新，等.苹果白兰地发酵工艺模型的建立[J].中国酿造，2011(5)：176-178.

Evaluation Model of Grape Wine Quality Based on Physicochemical Indexes

YE Si-ping1, CHEN Hai-guang2, LIANG Kai-hao3*

(1. Vocational Technical School of Conghua, Conghua, Guangzhou 510921; 2. College of Light Industry and Food, Zhongkai University of Agriculture and Engineering, Guangzhou, Guangdong 510225; 3.College of Computational Science, Zhongkai University of Agriculture and Engineering, Guangzhou, Guangdong 510225)

Quality of grape wine is an overall merit of its exterior, aroma and taste. Before, the evaluation of grape wine is from wine judgers. This paper studies physicochemical indexes of grape wine, including anthocyanin, total phenols and tannin, to evaluate the quality of wine. For the sake of eliminating effect of dimension of different indexes, the data of indexes need to be standardized. According to deviation maximizing principle, non-linear planning model of grape wine quality is established. Results show that physicochemical indexes can reflect the quality of wine in certain extent.

MSE criterion; Grape wine; Physicochemical indexes; NLP model

广东省教育厅育苗工程项目(2012WYM_0081)。

叶思平(1985- )，女，广东广州人，助教，硕士，从事食品安全与营养方面研究。*通讯作者，讲师，硕士，从事数学建模和金融工程方面研究。

2015-03-15

S 11+4

A

0517-6611(2015)12-214-03