传统Bayes 判别与非参数核密度Bayes 判别的比较

艾天霞， 张 蕾

(1.榆林学院 数学与统计学院，陕西 榆林719000;2. 云南师范大学文理学院 工商管理学院，云南昆明650222)

判别分析的基本思想是根据对已有的分类数据进行研究，找出样本数据的分类规律，然后建立判别函数，进而通过判别函数对新样本的分类情况进行判别的一种分类学科。根据是否需要事先假设总体的分布情况，判别分析分为参数判别分析和非参数判别分析。参数判别分析就是传统的判别分析，主要有距离判别、Bayes判别和Fisher 判别。非参数判别分析主要分为两种:一种是非参数核密度估计判别分析;另一种是非参数最近邻估计判别分析［1］。在参数判别分析方法中，Bayes 判别方法应用最为广泛;在非参数判别分析方法中，非参数核密度Bayes 判别方法最为普遍。下面介绍这两种判别分析的基本原理，并对这两种判别分析方法进行比较。

1 传统Bayes 判别分析

传统Bayes 判别分析主要讨论正态分布的情况。假设有k 个总体G1，G2，…，Gk，对应的概率密度函数分别为f1(x)，f2(x)，…，fk(x)，Xi服从均值为μi，协方差阵为∑i的正态分布，其中i = 1，2，…，k，Xi的密度函数为

相应的先验概率分别为p1，p2，…，pk，则有pi≥0 且p1+p2+…+pk= 1。提前假定所有的错判损失都相同，则多分类Bayes 判别的判别准则为［2］

2 非参数核密度Bayes 判别分析

在非参数核密度Bayes判别分析中，假设有k 个总体G1，G2，…，Gk，p 个指标，相应的核密度函数［3-4］分别为fn1(x)，fn2(x)，…，fnk(x)，先验概率分别为p1，p2，…，pk，假定所有的错判损失相等，采用SJ 带宽，并取核函数为高斯核函数，则总体Gj(j =1，2，…，k)的核密度估计［5-6］可表示为

其 中，i = 1，2，…，nj;j = 1，2，…，k;n = n1+n2+ … +nj;相应的先验概率的估计为

将先验概率的估计值代入多分类贝叶斯判别规则中，得到后验概率，然后进行比较。因此，非参数核密度贝叶斯判别规则为

3 传统Bayes 判别分析与非参数核密度Bayes 判别分析比较

3.1 两种判别分析方法的理论比较

传统Bayes 判别方法是一种参数判别方法，主要讨论总体服从正态分布的情形。采用传统Bayes判别方法时，需要事先假定总体服从正态分布。但是，在实际情况中，总体通常不服从正态分布，或者总体的分布情况是未知的，此时已不再适用传统Bayes 判别方法。非参数核密度Bayes 判别方法是一种非参数判别方法，运用非参数判别方法时，不需要事先假定总体的分布情况，而是直接通过数据本身来估计总体的概率密度，适用于任何分布形式的总体。从理论上来说，相比于传统方法，非参数核密度Bayes 判别方法具有更广泛的适用性。

3.2 两种判别分析方法的统计模拟

通过统计模拟的方法对传统Bayes 判别方法与非参数核密度Bayes 判别方法进行比较。若总体所考虑的指标有p 个，那么总体就是p 维数据，所采用的判别分析就是p 维判别分析。为了方便研究，文中仅仅模拟了p = 1 和p = 2 的情形，其他多维情形可以类似推导。

对于一维情形和二维情形，又分别模拟了正态数据和非正态数据，其中正态数据作为对照组，非正态数据作为比较组。总体中参数的取值情况不同，得到的数据也不一样。针对上述情形，文中将分别模拟参数的不同取值情况，以便更好地说明结果。

3.2.1 一维正态 用R 语言随机生成服从N(μ，σ2)的一维数据xi(i = 1，2，…，n)，其中针对参数μ和σ2的不同取值，模拟了以下6 种情况:(1)μ = 0，σ2= 1;(2)μ = 0，σ2= 0.5;(3)μ = 5，σ2= 1;(4)μ = 5，σ2= 0.5;(5)μ = 10，σ2= 1;(6)μ =10，σ2= 0.5。生成随机数据后，定义每组数据的原始分类情况，采用的方法是:求出每组数据的中位数，记为Me(xi)，对于i = 1，2，…，n，定义

则Si就是每组数据的原始分类情况。如果存在若干数据等于Me(xi)的情况，就需要剔除掉这几个数据，然后再重新生成几个随机数据，直至每组数据中没有等于中位数的情况为止，最后将保证类别1和类别2 的数据各占数据总量的一半。

3.2.2 一维非正态 不妨采用服从Gamma 分布的数据进行模拟。用R 语言随机生成服从Gamma(α，β)分布的数据xi(i = 1，2，…，n)，其中针对参数α 和β 的不同取值，模拟了以下6 种情况:(1)α = 2，β = 0.1;(2)α = 2，β = 0.5;(3)α = 2，β = 1;(4)α = 2，β = 2.5;(5)α = 2，β = 5;(6)α =2，β = 10.5。生成随机数据后，定义每组数据的原始分类情况，方法同上。

3.2.3 二维正态 用R 语言随机生成服从N2(μ，Σ)的二维正态数据，其中第一维数据xi1服从N(μ1，)，第二维数据xi2服从N(μ2，)，针对参数μ1，，μ2，的不同取值，模拟了以下6 种情况:。生成随机数据后，定义每组数据的原始分类情况，采用的方法是:令

求出yi的中位数，记为Me(yi)，最后，对于i = 1，2，…，n，定义

则Si就是每组数据的原始分类情况。如果存在若干数据等于Me(yi)的情况，就需要剔除再选，直至每组数据中没有等于中位数的情况为止，最后将保证类别1 和类别2 的数据各占数据总量的一半。

3.2.4 二维非正态 不妨采用混合分布组成的非正态二维数据，具体方法如下:先构造第一维数据xi1，用R 生成两组具有不同μ 和σ2的一维正态数据，第一组数据ri1服从N(μ1，)，第二组数据ri2服从N(μ2，)，其中μ1≠μ2且，再生成一组服从U(0，1)的均匀分布数据zi，对于i = 1，2，…，n

则xi1为第一维数据，同理构造第二维数据xi2。针对参数μ1，，μ2，，μ3，，μ4，σ24 的不同取值，模拟以下6 种情况:

生成二维随机数据后，定义每组数据的原始分类情况，方法同上。

3.2.5 模拟结果 利用随机生成的数据，采用两种判别方法进行判别分析。在统计模拟时，分别取样本容量n = 50，n = 200，n = 500 3 种情况，进行重复数N = 1 000 次的模拟试验，最后取1 000 次模拟结果的平均值作为最终结果。运行R 软件，得出每组数据的最终模拟结果，将两种判别方法的最终模拟结果进行比较。结果显示，在上述统计模拟的各种情形中，非参数核密度Bayes 判别方法的正判率都明显高于传统Bayes 判别方法的正判率。

3.3 两种判别分析方法的实证比较

3.3.1 对一组正态体检数据的判别分析 为研究冠心病，某位医生测定了15 例50 ～59 岁的冠心病人和15 例50 ～59 岁的正常人的舒张压和胆固醇指标(数据来源于《SPSS 宝典》16.3 实例数据［7］)。对这30例数据分别用两种判别方法进行判别分析，将分类结果与原始分类情况进行比较，结果如表1 所示。

表1 体检数据的两种判别结果比较Tab.1 Comparison of two discriminant results for physical examination data

表1 结果表明，在冠心病组的判别中，非参数核密度Bayes 判别方法的正判率是66.7%，高于传统Bayes 判别方法的正判率;在正常人组的判别中，两种方法的正判率都是100%。综合来看，非参数核密度Bayes 判别方法的正判率高于传统Bayes 判别方法。

3.3.2 对一组非正态企业财务数据的判别分析为研究企业财务预警［8-9］问题，随机选取了20 家被特别处理的上市公司(ST 公司)和180 家正常的上市公司(非ST 公司)作为研究对象(数据来源于Wind 资讯)。测定这200 家上市公司的8 个财务指标。对这8 个财务指标数据进行正态性检验，各指标数据都不服从正态分布。针对这200 例数据，分别采用两种判别方法进行判别分析，将分类结果与原始分类情况进行比较，计算出两种方法的正判率，结果如表2 所示。

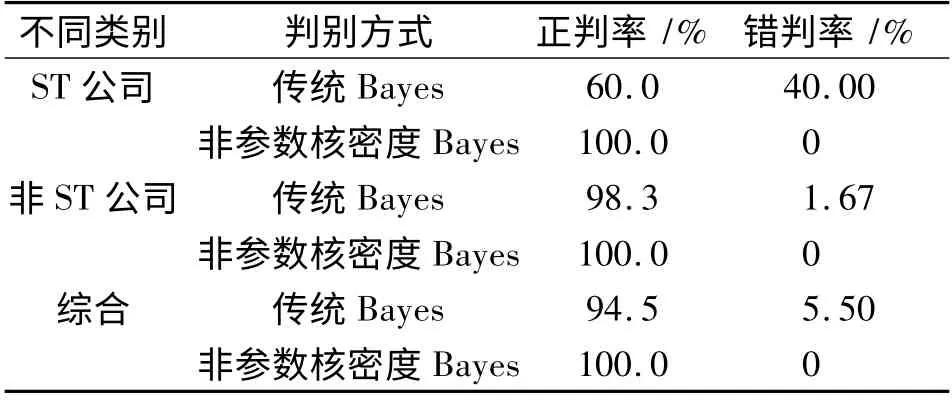
表2 企业财务数据的两种判别结果比较Tab.2 Comparison of two discriminant results for enterprise’s financial data

表2 结果表明，在ST 公司的判别中，非参数核密度Bayes 判别方法的正判率是100%，明显高于传统Bayes 判别方法的正判率;在非ST 公司的判别中，非参数核密度Bayes 判别方法的正判率略高于传统Bayes 判别方法的正判率。综合来看，非参数核密度Bayes 判别方法的正判率明显高于传统Bayes判别方法的正判率。

4 结 语

综上所述，非参数核密度Bayes 判别方法要明显优于传统Bayes 判别方法。从理论上看，当总体的分布情况已知，且服从正态分布时，传统Bayes 判别方法无疑是适用的;但当总体的分布情况未知时，此时应该采用非参数核密度Bayes 判别方法。非参数核密度Bayes 判别方法不需要事先假定总体的分布情况，所以适用范围更广。通过统计模拟和实证分析两方面验证，结果表明，当总体服从正态分布时，非参数核密度Bayes 判别方法的正判率不低于传统Bayes 判别方法的正判率;当总体不服从正态分布时，非参数核密度Bayes 判别方法的正判率远远高于传统Bayes 判别方法的正判率。可见，对于任何分布形式的总体来说，非参数核密度Bayes 判别方法都是有效的。

［1］朱干江.非参数密度估计在判别分析中的应用［D］.南京:南京信息工程大学，2007.

［2］薛毅，陈立萍.统计建模与R 软件［M］.北京:清华大学出版社，2007:375-397.

［3］马明卫，宋松柏.非参数方法在干旱频率分析中的应用［J］.水文，2011，31(3):5-12.

MA Mingwei，SONG Songbai.Nonparametric approach for drought frequency analysis［J］. Journey of China Hydrology，2011，31(3):5-12.(in Chinese)

［3］牛玉坤，胡晓华.基于非参数核估计方法的中国股市收益率分布研究［J］.湖南师范大学学报:自然科学版，2013，26(4):363-367.

NIU Yukun，HU Xiaohua. The Chinese stock market returns distribution research based on nonparametric kernel estimation method［J］.Journal of Hainan Normal University:Natural Science，2013，26(4):363-367.(in Chinese)

［5］ZHANG Jin，WANG Xueren.Robust normal reference bandwidth for kernel density estimation［J］.Statist Neerlandica，2009，63:13-23.

［6］Adamowskik.Nonparametric kernel estimation of frequencies［J］.Water Resources Research，1985，21(11):1585-1590.

［7］张庆利.SPSS 宝典［M］.2 版.北京:电子工业出版社，2011:214-287.

［8］罗怡，郑春伟.我国企业财务预警实证分析—以2012 年23 家金融机具上市公司为例［J］.财经科学，2014(2):88-95.

LUO Yi，ZHENG Chunwei.Financial warning empirical analysis of the financial instrument companies:evidence form 23 listed companies of 2012［J］.Finance and Economics，2014(2):88-95.(in Chinese)

［9］黄振，朱珺，张为.基于Bayes 判别分析法的上市公司财务风险研究［J］.洛阳理工学院学报:社会科学版，2012，27(3):26-28.

HUANG Zhen，ZHU Jun，ZHANG Wei. Research based on discriminative analysis of bayes into financial risks faced with the exchange-listed companies［J］.Journal of Luoyang Institute of Science and Technology:Social Science，2012，27(3):26-28.(in Chinese)