LCL 滤波并网逆变器的新型电流控制策略

何春花， 惠 晶

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡214122)

光伏并网逆变技术作为分布式发电系统并网的关键技术之一，对并网系统的安全稳定运行、电能质量控制以及电力系统的规划都至关重要［1-2］。光伏逆变器的脉宽调制(PWM)过程中会产生大量的开关频率次谐波，为提高并网电流质量，需要采用适当的滤波器［3］。常用滤波器有L 型、LC 型、LCL型滤波器。LCL 滤波器所需总电感量比L 和LC 滤波器小得多，运用LCL 滤波器不仅能降低成本，减小滤波器的体积和质量，还能提高动态响应能力，对谐波的抑制效果佳，具有较好的应用前景［4-5］。但LCL 滤波器是一个3 阶系统，本身存在着谐振问题而使系统不稳定。为了抑制谐振必须增加阻尼环节，而阻尼环节会带来系统功率损耗［6］。为提高逆变效率和供电质量，可以采用合适的控制方案来实现有源阻尼降低系统功率损耗同时抑制谐振，因此优化逆变器的控制策略是近年来研究的一个重点和热点。

文中采用并网电流和电容电流双闭环控制策略，用电容电流内环来增加系统阻尼，以有效抑制谐振发生，用进网电流外环控制实现对并网电流的直接控制，可保证高的进网电流功率因数。通过仿真验证，该方法具有良好的稳态和动态性能。

1 LCL 拓扑及并网电流控制策略

1.1 系统结构模型

LCL 滤波器以其所需电感量小、对高频谐波抑制能力强等优点受到广泛认可［7-8］。图1 所示是采用LCL 滤波器的三相并网逆变器拓扑结构，由逆变器侧电感L1、滤波电容C 和网侧电感L2组成，其中Udc是直流母线电压。控制方案采用并网电流作为外环，实现对并网电流的直接控制，可有效提高进网电流功率因数。电容电流作为内环，增加系统阻尼，抑制系统振荡，提高系统的动态性能，同时结合同步矢量电流比例-积分(Proportional Integral，PI)调节器的SVPWM 方法，实现开关管的导通与关断，使电压源型LCL 滤波并网逆变器输出电流的相位完全与电网电压相位一致，保证向电网输送电流的总谐波含量符合标准要求。

图1 三相LCL 滤波并网逆变器Fig.1 Three-phase grid-connected inverter with LCL filter

1.2 PWM 并网逆变器的数学模型

PWM 可以同时实现变频变压反抑制谐波，因此在交流传动及其它能量变换系统中得到广泛应用，并一直是研究的热点。而逆变桥开关管的控制模式又多种多样，因此不考虑具体开关器件的类别，建立PWM 逆变器的通用数学模型对系统仿真设计和验证具有重要意义。

为便于分析，作如下假设:(1)电路开关器件为理想开关元件;(2)所有续流二极管导通压降均为零;(3)在换相过程中，忽略晶体管开关时吸收电容的影响;(4)三相电网电压对称且稳定，直流侧电压纹波为零。这里首先用开关函数建立三相逆变全桥环节的通用数学模型，然后建立滤波器的数学模型，把两者直接相连即可构造出仿真模型。

定义各个开关函数:Sj= 1，第j 个开关导通，Sj= －1，第j 个开关断开，j = 1，2，3，4，5，6。则

其中k = 0，1，…，7。

设O 为直流电源负极电位点，求得每相逆变桥输出点a，b，c 到直流电源负极之间的电压与开关函数之间的关系为

根据基尔霍夫电压定理，由图1 可知

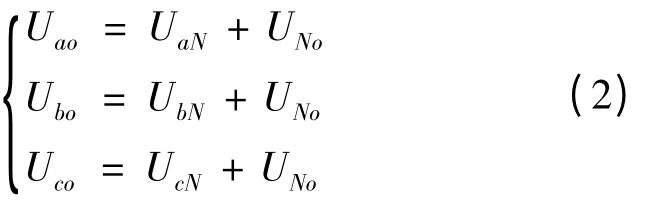
由先前假设可知，三相电压和负载是对称的，即UaN+ UbN+ UcN= 0 所以有

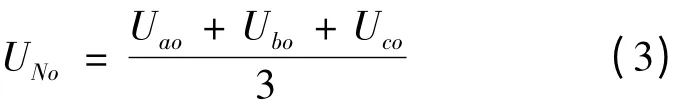
由式(1)～(3)定理可得

1.3 LCL 滤波器的数学模型

LCL 滤波器作用是利用加入的电容支路为高频开关纹波电流提供低阻通路，起到对高频分量的旁路作用，减少注入电网的纹波电流。分别选择电感L1中的电流i1k、电感L2中的电流i2k和滤波电容电压Uck为状态变量，其中k = a，b，c。图2 为每相LCL滤波器的传递函数结构图。

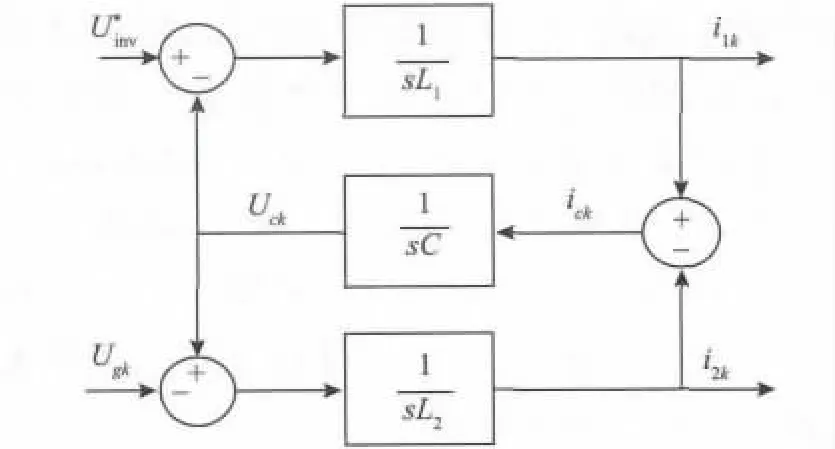
图2 每相滤波器模型Fig.2 Each phase filter model

其状态空间方程为

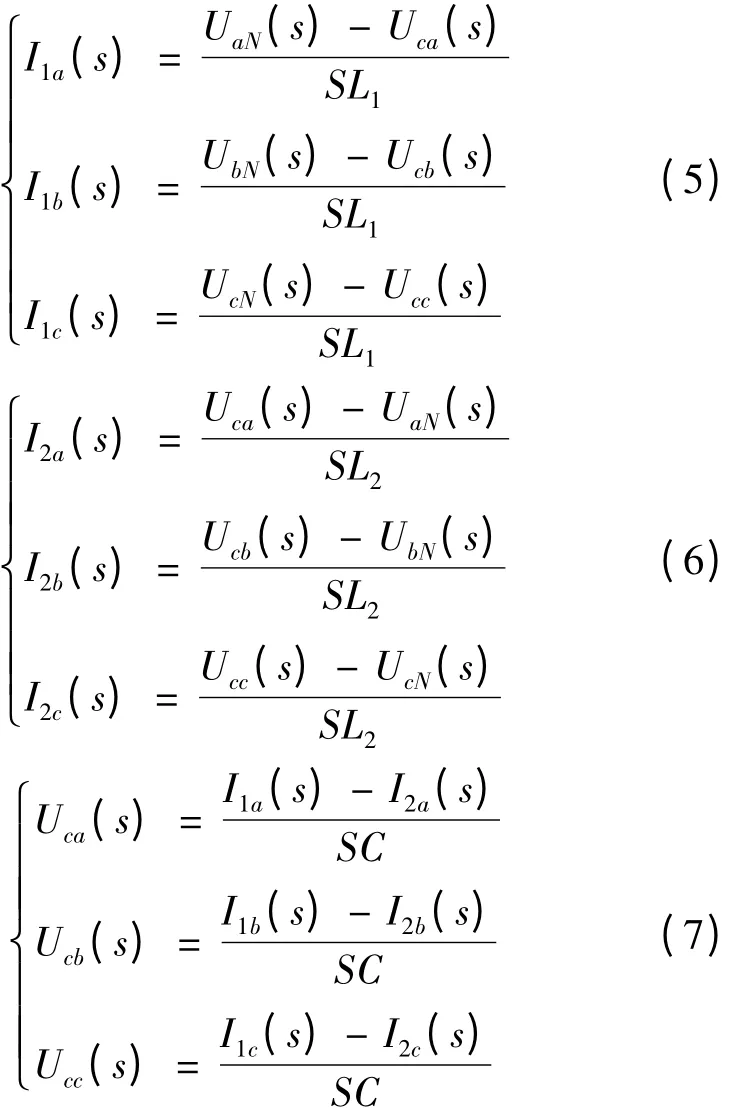
2 控制策略及其稳定性分析

2.1 系统原理框图及其稳定条件分析

从上述状态方程式可知，各相传递函数之间是相互独立的，并且其形式和单相逆变器状态方程是一致的。因此，该逆变电源系统的控制策略及其稳定性分析讨论可基于单相逆变器展开，为实现交流变量控制的零稳态误差，控制器采用无差拍控制器，能够实现无差跟踪，具有良好的动态性能［9］。

对于三相并网逆变器而言，控制策略的实现是通过变量导数预测控制结果，这样使用动态响应较快和鲁棒性较强的PI 调节器即可实现并网电流的无静差调节，使并网逆变器向电网输出高质量并网电流，且基于SVPWM 的同步矢量电流PI 控制方案对一些非线性因素的影响也具有一定的补偿功能［10］。

图3 给出文中所提逆变器并网运行控制方法的结构，图4 所示为电流双闭环控制的等效结构。

为便于系统的稳定性分析，设电流反馈均为单位反馈。其中，逆变桥相对于直流电源的等效输出增益为KPWM;比例控制环节为K。

图3 电容电流环的主要作用是增加系统阻尼，以有效抑制谐振发生，其控制器只需用比例控制即可，K 为比例系数。利用自动控制理论中的等效变换法将图3 等效变换，简化得到并网电流控制的等效结构如图4 所示。

由图4 可以看出，并网电流的质量不仅受电网电压自身谐波含量的影响，而且与电流控制策略有关。

图3 电流双闭环控制结构Fig.3 Current double closed-loop control structure diagram

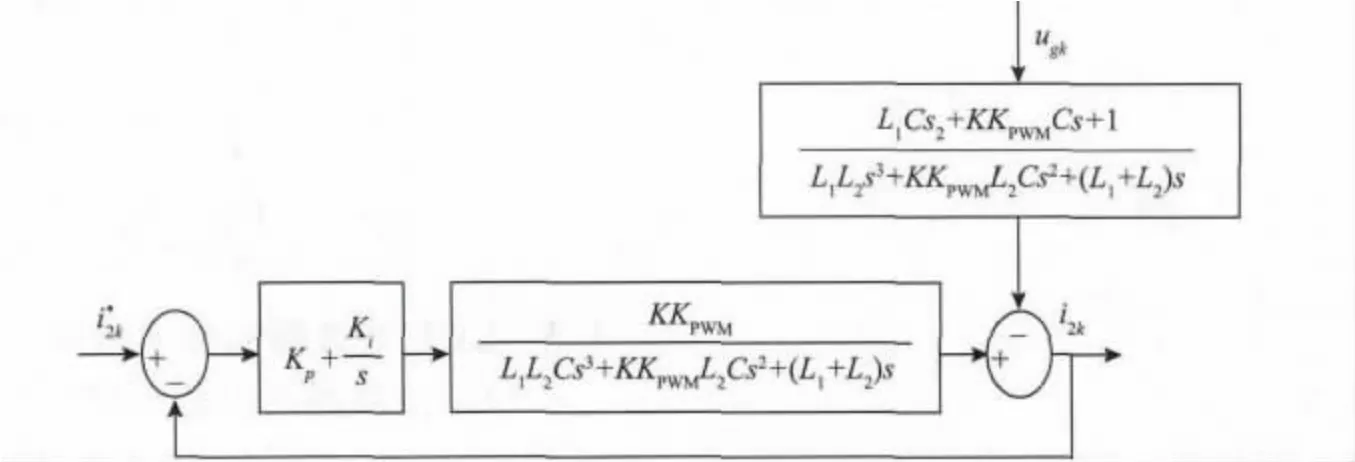
图4 电流双闭环控制的等效结构Fig.4 Structure diagram of the double closed-loop of current

文中主要研究电流控制策略对并网电流的影响，系统的开环传递函数为

为求出系统的稳定条件，由式(8)得到闭环传递函数

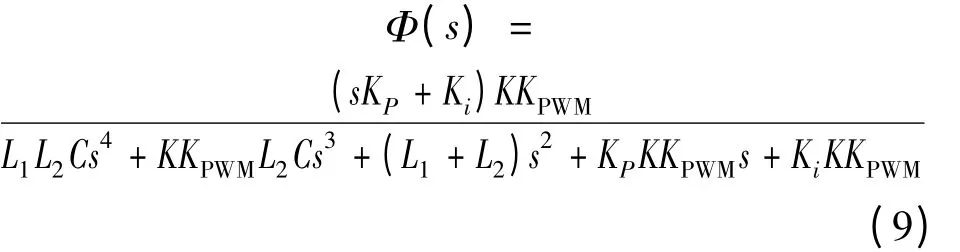
闭环系统传递函数的特征方程为

根据Hurwitz 稳定判据，系统稳定的充要条件为式(10)各项系数全大于零，且

由式(11)～(13)可以解出KP，Ki的临界值。

2.2 系统闭环参数设计与性能分析

LCL 滤波器为3 阶电路，系统稳态性能和动态性能受闭环参数的影响较大，所以设计的控制器参数要保证系统有足够的稳定裕度。根据控制原理，实际工程中一般要求幅值稳定裕度h 为5 ～10 dB，相角稳定裕度为25 ～60。由于文中控制策略中内环主要作用是增加系统阻尼，因此可以忽略高阶项，其特征阻尼比近似表示为

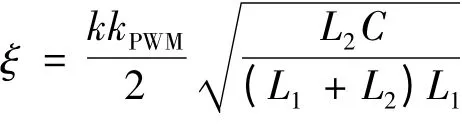
k 越大，系统阻尼比越大，谐振抑制效果越好，但是阻尼过大，系统快速性差，调节时间长。工程上往往取0.5 ＜ξ ＜1，但为了兼顾系统的阻尼效果和动态性能，一般取0.6 ＜ξ ＜0.8。考虑到实际系统参数L1，L2，C 与设计值可能存在一定程度的偏离，因为LCL 滤波器是利用了电感与电容对不同频率分量所呈现阻抗差异性的特点。与L 型滤波器相比，增加了滤波电容C 和网测电感L2，引入C 和L2后可对高次谐波的逆变器桥输出电流进行并联阻抗分流，滤波电容C 为高频部分提供低阻通路，从而有效降低入网电流中的谐波电流分量。但是，C 参数越大其需要的无功功率越多，相应导致逆变器的功率因数降低。通常用折衷值ξ = 0.707［11］。不同的L1，L2与C对滤波器频率特性的影响如图5 和图6 所示。

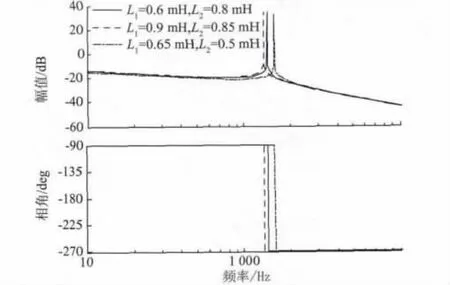
图5 C 不变L1，L2 取不同值的滤波器频率特性Fig.5 Filter frequency characteristic for constant C and different，L1 and L2

图6 L1 不变L2，C 取不同值时滤波器频率特性Fig.6 Filter frequency characteristic when constant L1 and different，C and L2

图5 是C = 10 μF 时的频率特性。可以看出，组合2 的滤波特性最好，组合3 的滤波特性比组合1 的差，虽然前者的L1比后者大，逆变桥电流中的高频含量相对较小，但过小的L2影响了分流效果，导致最终的滤波效果较差。

图6 是L1= 0.6 mH 不变且保证XC/XL2不变，改变L2与C 大小时滤波器的频率特性。从图中可以看出，3 种组合的频率谐振点不同，在转折频率以上的高频阶段，3 种组合的滤波性能几乎相同。改变L2后，由于改变了总的滤波电感量，3 种组合的低频段增益存在差异，滤波电感量越小则低频增益越高，电感造成的电压损越低。外环PI 调节器的设计方法比较多，文中结合KP，Ki的边界范围采用“振荡指标法”获得一组参数，以确保系统具有足够的稳定裕度，同时尽可能兼顾系统的动态性能。

3 仿真验证

为验证电感电流和电容电流双闭环控制策略的优越性，运用Matlab/Simulink 软件对LCL 并网逆变器的双闭环电流控制进行模型搭建并对其进行仿真，系统主要仿真参数如表1 所示。

表1 仿真参数Tab.1 Simulation parameters

图7 表示稳态运行时电网电压、并网电流和网侧电感电流的仿真波形。图8 是A 相并网电流的频谱分析。可以看出，网侧电流的相位与电网电压非常接近，系统实现了高功率因数并网运行，并且网侧电流THD 为1.02%，与网侧电感电流独立控制相比，很好地抑制了入网电流的谐波含量，获得了预期的电流输出效果。为验证系统的动态性能，在0.03 s 时突然增加并网电流。系统的动态仿真波形如图9 所示。可以看出，系统在半个周期内即可达到稳定状态，说明动态响应较快。

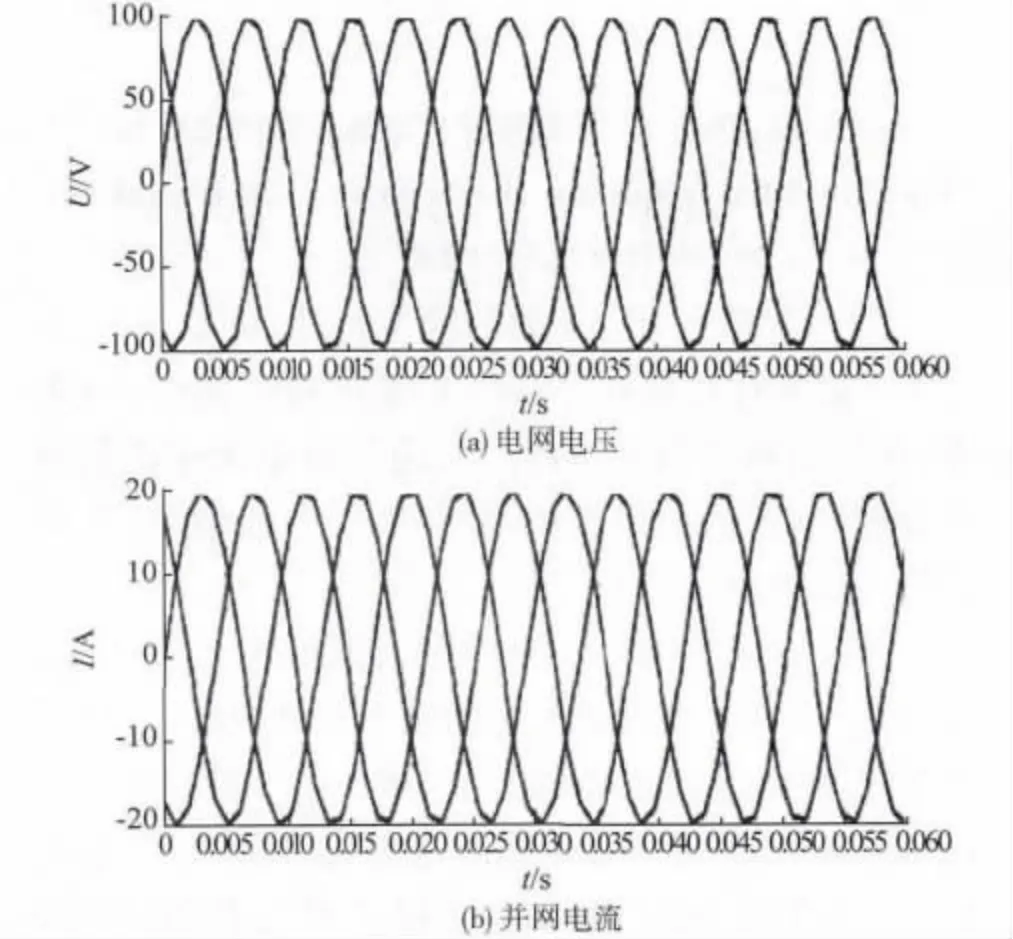
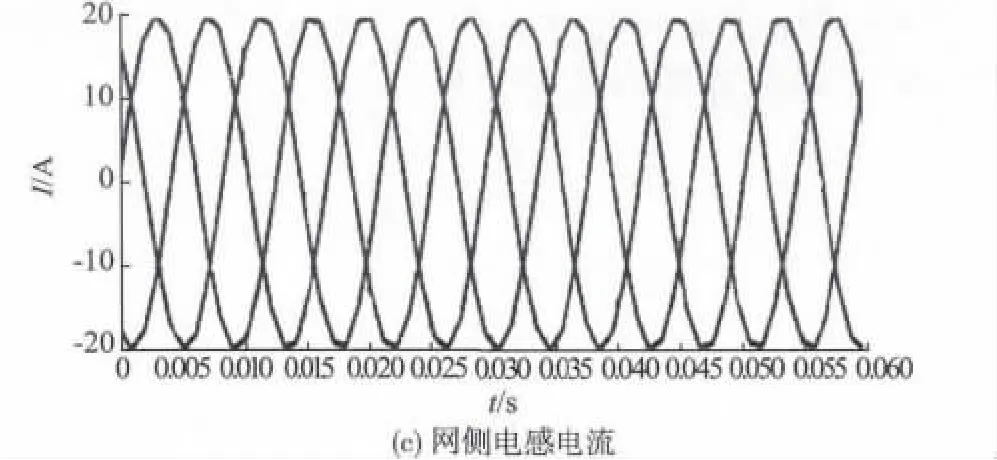
图7 稳态时仿真波形Fig.7 Simulation waveform in steady-states

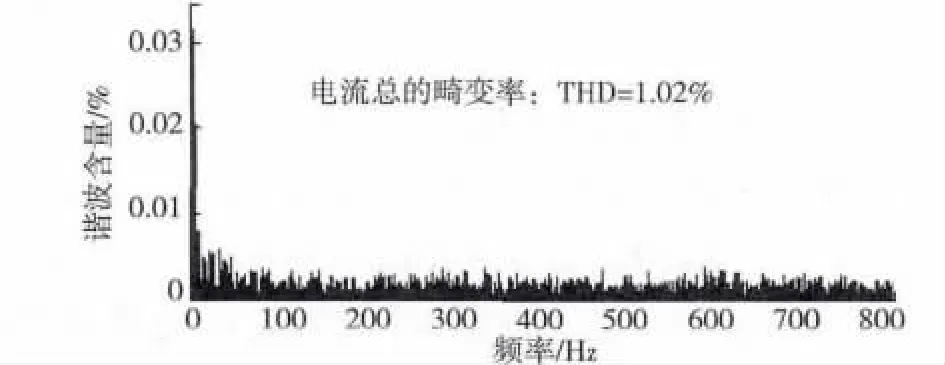
图8 a 相并网电流FFT 分析Fig.8 FFT analysis of the A-phase grid-connected current

图9 输出电流的动态仿真波形Fig.9 Dynamic simulation waveform of the output current

4 结 语

采用并网电流直接闭环控制的LCL 滤波逆变器并网系统存在谐振尖峰，易造成系统不稳定。文中采用网侧电感电流和电容电流相结合，提出并网电流作为外环、电容电流作为内环的控制策略。通过仿真表明，该控制策略既可有效抑制入网电流谐振和实现进网电流的高功率因数运行，同时又具有良好的稳态和动态性能，且方案简便易行。

［1］特奥多雷斯库.光伏与风力发电系统并网变换器［M］.周克亮，王政，徐青山，译.北京:机械工业出版社，2012.

［2］张兴，曹仁贤.太阳能光伏并网发电及其逆变控制［M］.北京:机械工业出版社，2011.

［3］陈东.并网逆变器系统中的重复控制技术及其应用研究［D］.杭州:浙江大学，2012.

［4］王国君.基于虚拟磁链直接功率控制的并网逆变器的研究［D］. 哈尔滨:哈尔滨工业大学，2008.

［5］赵方平，杨勇，阮毅，等.三相并网逆变器直接功率控制和直接功率预测控制的对比［J］. 电工技术学报，2012，27(7):212-220.

ZHAO Fangping，YANG Yong，RUAN Yi，et al. Comparative study for direct power control and direct power predictive control in three-phase grid-connected inverters［J］.Transactions of China Electrotechnical Society，2012，27(7):212-220.(in Chinese)

［6］韩咏茹，薛士龙，邓勇智.基于LCL 滤波的逆变器并网电流控制策略研究［J］.电源学报，2014，1(51):103-110.

HAN Yongru，XUE Shilong，DENG Yongzhi.Current control strategy for the grid-connected inverter with LCL filter［J］.Journal of Power Supply，2014，1(51):103-110.(in Chinese)

［7］郭小强，邬伟扬，顾和荣，等.并网逆变器LCL 接口直接输出电流控制建模及稳定性分析［J］. 电工技术学报，2010，25(3):102-109.

GUO Xiaoqiang，WU Weiyang，GU Herong，et al. Modelling and stability analysis of direct output current control for LCL interfaced grid-connected inverters［J］.Transactions of China Electrotechnical Society，2010，25(3):102-109.(in Chinese)

［8］TANG Yi，Poh Chiang Loh，WANG Peng，et al. Exploring inhere damping charae tefisfic of LCL-filters for three-phase gridconneetod voltage source inverters［J］.IEEE Tmnsactions on Power Electronics，2012，27(3):1433-1443.

［9］ZHANG X，Spencer J W，Guermro J M.Small signal modeling of digitally controlled grid-connected invertem with LCL filter［J］.IEEE Transactions on Industrial Electronics，2013，60(9):3752-3765.

［10］艾淑云，翟登辉，李献伟，等.基于无差拍算法的单相光伏并网逆变器的研究［J］.通讯电源技术，2014，31(3):4-6.

AI Shuyun，ZHAI Denghui，LI Xianwei.Research on single-phase photovoltaic grid-connected inverter based on deadbeat control［J］.Telecom Power Technology，2014，31(3):4-6.(in Chinese)

［11］Jeong Hea-Gwang，Lee Kyo-Beum，Choi S. Performance improvement of LCL filter based grid-connected inverters using PQR power transformation［J］.IEEE Trans On Power Electronics，2010，25(5):1320-1330.