一种快速小盲区的主动移频式孤岛检测方法研究

陈超波，李继超，高 嵩，宋 鹤

（西安工业大学电子信息工程学院，西安710021）

引言

孤岛效应［1-3］是指当电网因故中断供电时，独立的光伏并网发电系统仍与本地负载形成一个自给供电的孤岛发电系统。光伏并网发电系统处于孤岛运行状态时，可能会损坏电气设备，严重时甚至会危及电网及维修人员的人身安全［1-4］。因此研究一种有效的孤岛检测方法，既能快速、准确地检测出孤岛，又尽量减小对并网电能质量产生的不良影响，对避免孤岛发生时所带来的严重危害具有十分重要的现实意义。

国内外目前所研究的孤岛检测方法主要为被动式和主动式两大类。被动式检测法利用逆变器输出端电压或频率等的异常来判断孤岛发生，包括过/欠压 OVP/UVP（over voltage protection/under voltage protection）和过/欠频 OFP/UFP（over frequency protection/under frequency protection）等方法［2］； 主动式检测法通过对逆变器输出施加扰动，根据监测PCC点电压幅值、频率等量的变化来判断孤岛发生。主动频率偏移法［3］AFD（active frequency drift）是最基本的主动移频式孤岛检测方法。文献［4］提出一种带正反馈的主动频率偏移法AFDPF（active frequency drift with positive feedback），通过引入频率正反馈，加快孤岛检测速度快，但频率扰动方向单一，当负载呈容性时，该方法易失效，即存在检测盲区；文献［5］介绍了一种周期性不间断地对逆变器输出电压进行正反两个方向的频率扰动的AFDPF法，有效避免对单一频率扰动方向的平衡作用的问题，但孤岛检测速度较慢。

本文在分析AFD及AFDPF检测方法基本原理及检测性能的基础上，对AFDPF算法参数进行改进，提出一种小盲区的快速主动移频式孤岛检测方法，进一步提高孤岛检测速度，减小检测盲区。采用Qf0×Cnorm对3种主动移频式算法的孤岛检测盲区进行对比分析，搭建了Matlab/Simulink系统仿真模型，选取有效参数对改进算法孤岛检测性能的有效性进行进一步验证。

1 AFDPF法原理简析

1.1 AFD法的基本原理

AFD孤岛检测方法是以公共耦合点PCC（point of common coupling）处电压频率为输出电流的参考信号，在并网逆变器输出电流的正负半波尾部注入一定的死区时间tz，使其频率呈现增大或减小的趋势来进行孤岛检测，检测原理如图1所示。

图1 AFD原理Fig.1 Principle of AFD

以斩波因子cf来表征频率扰动强度大小，即

式中：tz为死区时间，表示电流过零点超前（或滞后）公共点电压过零点的时间间隔；TVpcc为公共点电压的周期。

在AFD算法中，cf为固定值，若设置过小，则不能在规定时间内检测出孤岛，增大孤岛检测盲区；若设置过大，虽能很快检测出孤岛，减小检测盲区，但同时也会使并网逆变器输出电流的总谐波畸变率 THD（total harmonic distortion）增大。

1.2 AFDPF法的基本原理

AFDPF在AFD的基础上，引入每一个周期PCC点电压频率与电网电压额定频率之差，给cf以频率正反馈，使cf的值不断增大，加速PCC点电压频率偏离正常值，实现孤岛检测。第i个周期的扰动量大小cfi可表示为

式中：cfi为第i个周期的频率扰动量；cf0为初始扰动量；k为正反馈增益；fi为第i个周期PCC点的电压频率；fg为电网电压额定频率。

与AFD法相比，AFDPF法提高了孤岛检测速度，减小了检测盲区；与AFD法一样，AFDPF法只适合纯阻性或呈感性负载的孤岛检测，对容性负载的检测仍存在很大的盲区［6］。

2 改进AFDPF法

2.1 改进AFDPF法原理

基于对AFDPF基本原理的分析，本文提出一种改进的AFDPF孤岛检测方法。该方法以第i个周期（包括第i个周期）以前的频率变化量累加值的绝对值作为正反馈量，以第0周期PCC点电压频率与电网电压额定频率之差的符号作为初始斩波因子及正反馈量的系数，其算法可表示为

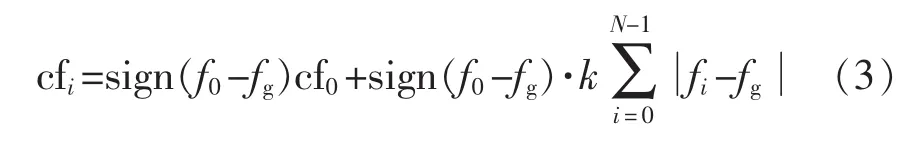
式中：f0为孤岛发生初始时刻PCC点电压频率；N为孤岛检测的周期数；sign（f0-fg）为初始时刻PCC点电压频率与电网电压额定频率之差的符号，由负载的性质决定，即：阻感性负载时，电压相位超前于电流相位，逆变器会不断增大输出电流的频率使得电压与电流同相位，此时f0-fg＞0；阻容性负载时，电压相位滞后于电流相位，逆变器会不断减小输出电流的频率使得电压与电流同相位，此时f0-fg＜0；纯阻性负载时，电压与电流同相位，此时f0-fg=0。则有

在电网断开初始时刻，检测当前PCC点电压频率f0，与电网电压额定频率fg进行比较，由其差值符号sign（f0-fg）确定初始斩波因子及正反馈量系数（即扰动方向），让二者扰动方向一致，从而进行叠加，加速PCC点频率偏移。对前i个周期PCC点电压频率与电网电压额定频率变化量取绝对值后进行累加，将累加值作为正反馈量，可有效避免由于电网扰动或外界其他因素干扰而引起的误判，使扰动量始终以初始时的扰动方向对PCC点电压频率进行扰动，以此形成正反馈，进一步加速公共点的电压频率偏移至孤岛保护阈值，检测出孤岛，触发过频/欠频保护。

2.2 改进AFDPF算法步骤

我国的单相交流电其电压额定有效值是220 V。根据GB/T 19939-2005规定：电网额定频率为50 Hz，孤岛保护阈值为 50±0.5 Hz，检测时间不超过 0.2 s。在此标准下，设计改进AFDPF算法步骤如下。

步骤 0 初始化初始斩波因子cf0=0.01，正反馈增益k=0.06，检测周期数i=0，电网额定频率fg=50 Hz，孤岛保护阈值上下限分别为fup=50.5 Hz、fdown=49.5 Hz。根据孤岛检测时间标准要求检测时间不超过0.2 s，因此改进AFDPF算法对单个扰动方向的孤岛检测。需在5个周期（0.1 s）内完成，则设置单个扰动方向的最大检测周期数Nmax=5。

步骤1 检测PCC点电压频率fi，利用第0周期的频率f0与电网额定频率fg之差的符号sign（f0-fg）来确定初始斩波因子及正反馈量对PCC点电压频率施加扰动的方向，即：f0-fg≥0，则 sign（f0-fg）=1，扰动量使 PCC 点频率向上偏移；fi-fg＜0，sign（f0-fg）=-1，则使PCC点频率向下偏移。

步骤2 检测并判断PCC点电压频率fi是否满足 49.5 Hz＜fi＜50.5 Hz。 若满足，则需要主动施加频率扰动，顺序执行步骤3；若不满足，即fi≥50.5 Hz或fi≤49.5 Hz，则说明孤岛已发生，则跳转至步骤 5。

步骤3 根据sign（f0-fg）符号确定单个方向的频率扰动量cfi为或cfi=-cf0-k对PCC点电压频率施加扰动。扰动完成后执行步骤 4。

步骤4 判断单个扰动方向的检测周期数i是否超过最大检测周期数Nmax。若i≥Nmax，即在当前的扰动方向下，未检测到孤岛，说明未发生孤岛，将检测结果直接返回；若i＜Nmax，则继续按照初始的扰动方向对PCC点电压频率施加扰动，并回到步骤2，进入循环。

步骤5 关闭逆变器，并返回。

采用此算法，不管是平衡负载，还是感性或者容性负载，均可根据sign（f0-fg）进行判别，从而施加有效的扰动算法，加快PCC点电压频率的变化，使频率迅速地偏移，触发UFR/OFR，从而快速检测出孤岛。

3 孤岛检测盲区

孤岛检测盲区的大小是评价一个孤岛检测方法性能的重要指标之一。孤岛检测盲区即为易引起某一孤岛检测方法检测失败的某些负载组合的集合［7］。针对不同的孤岛检测方法，常用4种不同坐标系下的检测盲区来描述其有效性［8］。经过分析比较，采用Qf0×Cnorm坐标系［9］对算法的孤岛检测盲区分布进行描述，不仅能反映孤岛检测性能受负载品质因数影响的情况，并且使盲区的图形表现力更强。

3.1 3种方法的检测盲区分布

文献［10］给出了相角判据方程，由文献［9］的分析推导，并根据GB/T 15945-1995规定的电网电压额定频率fg=50 Hz，允许的频率正常波动范围Δf为-0.5～0.5 Hz，可计算出 3 种方法的检测盲区分布。

（1）AFD盲区分布。AFD盲区的电容值范围为

式中：ωg为电网额定角频率，ωg=2πfg=100π；Cnorm为电容的标幺值；Qf0为类似负载品质因数［11］，与Qf含义完全不同。由式（5）得到AFD盲区分布如图2所示。

图2 AFD的孤岛检测盲区分布Fig.2 Island non-detection zone distribution of AFD

（2）AFDPF 盲区分布。将式（2）及 Δf的上、下限代入式（5）可得到AFDPF盲区的电容值范围为

由式（6）得到AFDPF盲区分布如图3所示。

图3 AFDPF的孤岛检测盲区分布Fig.3 Island non-detection zone distribution of AFDPF

（3）改进 AFDPF 盲区分布。 由式（3）、式（5）、式（6），可推算出改进AFDPF的盲区分布。

对于感性负载，盲区的电容值范围为

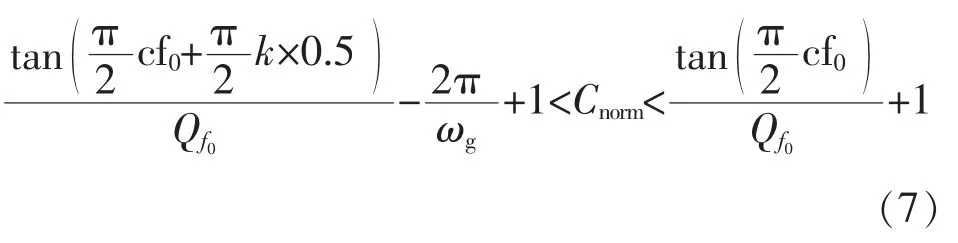
对于容性负载，盲区的电容值范围为

设置 cf0=±0.02，k=0.07，由式（7）、式（8），改进AFDPF的盲区分布如图4所示。

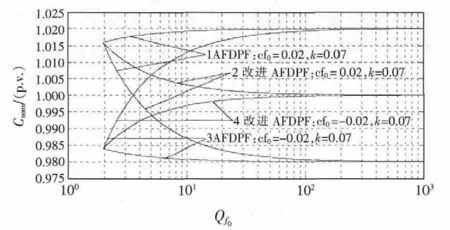
图4 改进AFDPF的孤岛检测盲区分布Fig.4 Island non-detection zone distribution of improved AFDPF

3.2 检测盲区分布图的分析

在图2～图4中，曲线包围部分为孤岛检测盲区。由图2、图3可见，cf0几乎不改变NDZ的大小，但能改变NDZ在负载平面上的位置，随cf0增大，NDZ位置向上移动；由图3可以看出，随正反馈增益k的增加，盲区向右减退，引起检测失败的负载参数区域减小；由图2～图4可见，检测盲区的大小依次为：AFD＞AFDPF＞改进AFDPF； 图2、 图3表明，AFD和AFDPF只适合非容性负载的孤岛检测，图4表明改进AFDPF不仅适合感性负载的孤岛检测，同时也适合容性负载的检测，并且相比前两种孤岛检测算法，具有更小的NDZ。

4 仿真分析

4.1 算法参数选取

正反馈增益k的选取：由以上对盲区的描述可知，增大正反馈增益k数可有效减小孤岛检测盲区，但过大的增益会增大电流畸变［12］。因此k值的选取需同时兼顾盲区与电流畸变的有效性。由文献［13］的分析，在利用AFDPF法检测孤岛时，必须满足 k ＞0.053 1，常设置 k=0.07，此时，对电能质量影响较小，且检测效率较高。对于改进的AFDPF，由于正反馈量的增加，会比AFDPF的电流THD大，因此选取改进AFDPF的正反馈增益k=0.06，在兼顾检测盲区较小的同时，可有效减小由于反馈量增加而引起的电流畸变。

初始扰动值cf0的选取原则是：cf0的改变对检测盲区的大小影响不大，但直接影响着PV系统输出电流的谐波水平及孤岛检测速度。由文献［14］中对cf0和电流THD之间的关系分析可知，二者接近线性关系，因此cf0不宜取值过大，一般cf0=0.01或0.02。对于孤岛检测时间而言，cf0越大，检测时间越短。本文算法在引入正反馈的基础上进一步增大了正反馈量，可快速将频率推离至孤岛保护阈值，兼顾检测时间与电能质量的考虑，cf0不宜过大，取为cf0=0.01。

4.2 仿真结果分析

为了验证本文所提出的改进AFDPF法在电网断开后能够快速可靠地检测出孤岛，在Matlab/Simulink环境下建立了孤岛仿真模型，仿真模型如图5所示，逆变器输出采用恒电流控制模式。

图5 孤岛检测仿真模型Fig.5 Simulation model of islanding detection

模型参数设置为：输入直流电压400 V，电网电压有效值220 V，频率50 Hz，逆变器输出电流经LC滤波器滤波后与本地负载及电网链接，L=6 mH，C=3 μF，在最恶劣的工况环境下配置本地负载参数，RLC并联负载的有功功率为2 kW，负载品质因数Qf0=2.5，负载固有谐振频率为 50 Hz；分别调整本地负载为感性和容性，在0.08 s时断开电网。对改进算法进行Matlab/Simulink仿真，电网断开后，两种负载情况下PCC点电压、逆变器输出电流波形及PCC点电压频率分别如图6、图7所示。

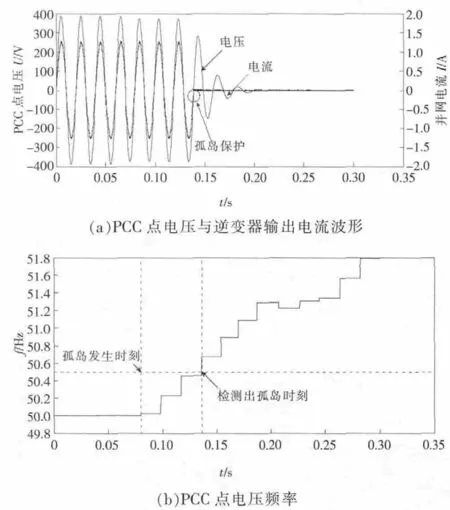
图6 阻感负载情况下的仿真结果Fig.6 Simulation results of reactive location loads

由图6可见，在0.08 s前，光伏系统处于并网运行状态，逆变器输出电流与电网电压始终保持同频同相，电网断开瞬间，负载谐振频率等于电网电压频率，即fi-fg=0。仅在cf0的作用下，PCC点电压频率正向偏移，此后，在cf0及正反馈的共同作用下，PCC点电压频率持续偏移，在0.14 s时AFDPF将电压频率推离至50.5 Hz，检测出孤岛，发生欠压保护，逆变器封锁功率管的输出，电压、电流衰减至0，检测时间为 0.06 s，比传统 AFDPF 检测时间［6］提高 0.12 s。

图7 阻容负载情况下的仿真结果Fig.7 Simulation results of active location loads

由图7可见，在负载呈阻容性时，此时f0-fg＜0，cf0与正反馈扰动的方向相反，传统AFDPF在0.2 s 内无法检测出 孤岛［6］，而改进算法则直接根据负载的性质自动调整cf0的扰动方向，使其与正反馈扰动方向一致，并且通过正反馈量的累积，使PCC点电压频率迅速向下偏移，在0.12 s时检测出孤岛，仅需0.04 s，有效消除了由于负载性质不同而引起的检测盲区。

为进一步验证改进算法的检测性能，对并网逆变器输出电流进行FFT分析，分析结果如图8所示。

改进算法中，由于正反馈量的增加，使得扰动量cfi增大，从而导致并网逆变器输出电流畸变率稍大于传统 AFDPF的THD，GB/T 14549-1993规定，电流畸变率小于5%，因此，改进算法符合孤岛检测电能质量要求。

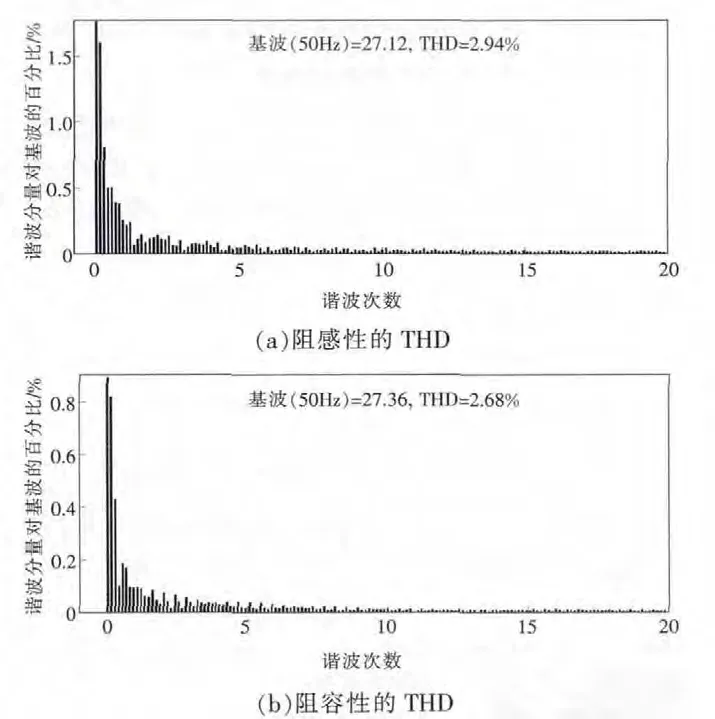
图8 并网逆变器输出电流的FFT分析Fig.8 FFT analysis of grid-connected inverter output current

5 结语

本文在传统AFDPF检测方法原理分析的基础上，通过对初始斩波因子、正反馈系数及正反馈量进行改进，提出了一种改进的AFDPF孤岛检测方法，以Qf0×Cnorm坐标系对新算法检测盲区进行了描述，并搭建Matlab/Simulink孤岛仿真模型，验证了该方法的有效性。仿真结果表明，该方法能在满足孤岛检测要求的情况下，能快速、准确地检测出孤岛。对于本文提出的改进算法，还可以通过与智能算法相结合，自适应地选取算法参数，对算法进行进一步的改进与完善。

［1］罗振环,杨富文.一种新型偶次谐波注入的主动式孤岛检测方法［J］.电源学报,2014,12（1）：15-22.Luo ZhenHuan,Yang FuWen.A new islanding detection method based on even harmonics injection［J］.Journal of Power Supply,2014,12（1）：15-22（in Chinese）.

［2］谢东.分布式发电多逆变器并网孤岛检测技术研究［D］.合肥：合肥工业大学,2014.Xie Dong.Research on Islanding Detection Technology for Multi-Grid Connected Inverter Based Distributed Generation［D］.Hefei ：Hefei University of Technology,2014（in Chinese）.

［3］Ko M J,Choy I,Choi J Y,et al.Simulation of active frequency drift adding zero current method for islanding detection［C］//2006 IEEE Power Electronics Specialists Conference,IEEE,2006：1-5.

［4］Ropp M E,Begovic M,Rohatgi A.Analysis and performance assessment of the active frequency drift method of islanding prevention［J］.Energy Conversion,IEEE Transactions on,1999,14（3）：810-816.

［5］John V,Ye Z,Kolwalkar A.Investigation of antiislanding protection of power converter based distributed generators using frequency domain analysis［C］//2003 IEEE Power Engineering Society General Meeting.IEEE,2003：4.

［6］郑涛,袁飞,王燕萍,等.基于模糊控制的快速无盲区的频移式孤岛检测法［J］.电力系统保护与控制,2014，42（23）：38-43.Zheng Tao,Yuan Fei,Wang Yanping,et al.A fast frequency drifts islanding-detecting method without non-detecting zone based on fuzzy control［J］.Power System Protection and Control,2014，42（23）：38-43（in Chinese）.

［7］刘芙蓉,康勇,段善旭,等.主动移频式孤岛检测方法的参数优化［J］.中国电机工程学报,2008,28（1）：95-99.Liu Furong,Kang Yong,Duan Shanxu,et al.Parameter optimization of active frequency drift islanding detection method［J］.Proceedings of the CSEE,2008,28（1）：95-99（in Chinese）.

［8］程明,张建忠,赵俊杰.分布式发电系统逆变器侧孤岛检测及非检测区描述［J］.电力科学与技术学报,2008,23（4）：44-52.Cheng Ming,Zhang Jianzhong,Zhao Junjie.Anti-islanding detection of power converter based distributed generation systems and mapping method of non-detection zones［J］.Journal of Electric Power and Technology,2008,23 （4）：44-52（in Chinese）.

［9］刘芙蓉,康勇,段善旭,等.一种有效的孤岛检测盲区描述方法［J］.电工技术学报,2008,22（10）：167-172.Liu Furong,Kang Yong,Duan Shanxu,et al.A novel method for mapping non-detection zone［J］.Transactions of China Electrotechnical Society,2007,22（10）：219-223（inChinese）.

［10］Ropp M E,Begovic M,Rohatgi A,et al.Determining the relative effectiveness of islanding detection methods using phase criteria and non-detection zones［J］.IEEE Transactions on Energy Conversion,2000,15（3）：290-296.

［11］LopesL,SunH.Performanceassessmentof active frequency drifting islanding detection methods［J］.IEEE Transactions onEnergyConversion,2006,21（1）：171-180.

［12］蒋翠,祁新梅,郑寿森.带电压频率正反馈的主动移频式孤岛检测方法［J］.电力系统保护与控制,2014,42（8）：95-100.Cui Jiang,Qi Xinmei,Zheng Shousen.Active frequency drift islanding detection with positive feedback of voltage frequency［J］.Power System Protection and Control,2014,42（8）：95-100（in Chinese）.

［13］刘方锐,康勇,张宇,等.带正反馈的主动移频孤岛检测法的参数优化［J］.电工电能新技术,2008,27（3）：22-25.Liu Fangrui,Kang Yong,Zhang Yu,et al.Parameter optimization of active frequency drift with positive feedback islanding detection method［J］.Advanced Thecnology of Electric Engineering and Energy,2008,27（3）：22-25（in Chinese）.

［14］王晓寰,张修北,董杰,等.基于0-1序列的三相并网逆变器孤岛检测方法［J］.电源学报,2014,12（6）：86-92.Wang Xiaohuan,Zhang Xiubei,Dong Jie.Active islanding detection method based on 0-1 sequence for threephase grid-connected inverter［J］.Journal of Power Supply,2014,12（6）：86-92（in Chinese）.

［15］Yafaoui A,Wu Bin,Kouro S.Improved active frequency drift anti-islanding detection method for grid connected photovoltaic systems［J］.Power Electronics,IEEE Transactions on,2012,27（5）：2367-2375.

［16］邓燕妮,桂卫华.一种低畸变的主动移频式孤岛检测算法［J］.电工技术学报,2009,24（4）：219-223.Deng Yanni,Gui Weihua.An improved active frequencydrift method for islanding detection for islanding detection with low harmonics distortion［J］.Transactions of China Electrotechnical Society,2009,24（4）：219-223（in Chinese）.