基于自校正LS-SVM的电厂锅炉烟气含氧量软测量系统

唐振浩 段 洁 曹生现 王 恭

(东北电力大学自动化工程学院，吉林 吉林 132012)

根据国家能源局2015年发布的信息，我国2014年火力发电设备容量为91 615万千瓦，约占全口径发电设备容量的67.32%，这说明火力发电仍然是我国当前最主要的发电方式。火电厂锅炉生产过程的重要指标是锅炉烟气含氧量，烟气含氧量过高锅炉热效率会降低，烟气含氧量过低则煤炭不能完全燃烧，影响锅炉热效率的同时也容易造成排放物超标[1]。因此控制火电厂锅炉烟气含氧量在合理范围内，保持锅炉在最佳的运行状态，是电厂降低燃料消耗和污染排放的重要手段。为了实现火电厂锅炉烟气含氧量的高精度控制，就要实时高精度获取相关的检测信息。目前常用的烟气含氧量检测方法有：磁式氧气传感器和氧化锆氧气传感器。这两类传感器的安装环境高温高噪声，所以经常要校正或更换传感器，而且检测结果的传输也比较滞后。

为了解决传统传感器技术的不足，软测量技术成为火电厂锅炉烟气含氧量控制的重要技术之一[2,3]。卢洪波等对电站锅炉飞灰含碳量进行建模估计[4,5]，李少华等对锅炉烟气中CO的含量基于神经网络进行建模[6]；在锅炉烟气含氧量软测量方面，湛腾西、袁俊文及韩璞等分别提出改进的神经网络方法进行建模，并取得了一定的成果[7～9]；王刚等采用差分进化和序列最小优化算法(Sequential Minimal Optimization，SMO)相结合的方法实现烟气含氧量的软测量[10]。文献[11～14]分别设计了基于支持向量机和最小二乘支持向量机的软测量方法。这些方法虽然都取得了一定的成果，但在测量精度方面仍有改进空间。

为此，笔者提出一种基于差分进化算法的自校正LS-SVM算法建立软测量模型，首先根据已有经验和实际数据分析选取适当的过程变量，并考虑含氧量变化的时序特点建立建模数据库；然后根据问题特点，采用差分进化算法校正LS-SVM参数；对差分进化算法进行改进，改善算法局部寻优能力，获取更高的测量精度；最后对该方法进行了验证。

1.1 电厂锅炉生产过程

电厂锅炉生产过程具有强非线性及时变性等特点，其生产过程可以简单概括为进料、燃烧和废气排放3个部分，如图1所示。在进料过程中，被磨煤机研磨成的煤粉经一次风机通过管道送入给粉机，煤粉经过给煤机送入炉膛燃烧。燃烧过程产生的热量将炉内水冷壁中的水加热形成水蒸气。燃烧结束后产生的烟气经引风机排出。

图1 电厂锅炉生产过程简图

1.2 烟气含氧量数据分析

电厂锅炉生产过程复杂，通过机理分析可知对烟气含氧量影响较大的因素有给水流量、燃料量、主蒸汽流量、主蒸汽压力、送风量、引风量、送风机电流、引风机电流、机组负荷、再热蒸汽温度及排烟温度等。由于炉况和实际生产环境的不同，这些影响因素与烟气含氧量在实际生产过程中的相互关系也不稳定。

针对不同炉况，用现场采集数据进行相关性分析，采用Pearson相关性分析法对影响因素和烟气含氧量之间的相关性进行分析，同时对实际生产数据进行相关性分析，从分析结果中选取0.01和0.05水平显著相关的变量作为建模输入量。选取主蒸汽压力、机组负荷、排烟温度、引风机电流、送风量、给水流量、炉膛负压、炉膛温度和再热器温度作为所研究锅炉的主要影响因素；由于温度变化具有时序特征，某一时刻温度与前N时刻的温度相关，经过相关性分析，在实验中选取N为5。在此共选取了14个参数作为输入变量构造锅炉烟气含氧量软测量模型。

2 烟气含氧量数据解析建模

2.1 数据预处理

实际生产中获取的数据存在噪声数据和数据缺失现象，为此采取相应的处理方法：

a. 对数据中的噪声进行处理。对建模时间段内不同参数的数据进行统计分析，计算各参数的期望μ和标准差σ。根据拉依达准则，将数值中在[μ-3σ,μ+3σ]区间之外的数据删除，根据含氧量数据连续变化的特征，用删除时刻前后两个时刻的平均值代替该数据。

b. 对数据缺失进行处理。由于检测设备故障或信号传输异常，实际获取的数据常有数据缺失的情况，对缺失数据采用均值插补法进行处理，将缺失时刻前后两个时刻的平均值填补缺失数据。

2.2 算法整体结构

基于DE优化的自校正LS-SVM算法中的LS-SVM算法根据DE粒子信息设定计算参数，采用建模数据库数据建立预测模型，并计算所得模型预测值的相对误差，该误差作为相应粒子的适应度函数值。

2.3 算法实现

基于DE优化的自校正LS-SVM算法流程如图2所示，具体实施步骤如下：

a. 将建模数据读入内存，采用2.1节所述方法对建模数据进行预处理。

b. 初始化差分进化算法，首先随机生成种群个数为NP、粒子维数为ND的种群(ND为所需优化参数的个数)，然后初始化DE算法参数F=0.4(F为缩放因子，控制搜索速度，其值越大搜索速度越快)。

c. 计算粒子适应度函数值，将预测误差作为对应粒子的适应度值，首先根据粒子信息为LS-SVM参数赋值；然后采用5-fold方法计算对应模型的平均测量误差，将建模数据分为5份，用其中的4份建立软测量模型，剩余一份作为检验数据，根据所建模型计算得到测量误差，重复进行5次并计算5次测量误差的平均值作为对应粒子的适应度函数值。

图2 基于DE优化的自校正LS-SVM流程

d. 如果粒子适应度值即所建立模型的测量误差达到终止条件，则停止算法，输出模型参数信息；如果没有达到终止条件，则进行粒子交叉、变异、选择操作，执行步骤c。

步骤d中，算法达到最大迭代次数NLOOP；算法最优解在指定代数NNF内不更新；算法计算时间达到指定时间NMAXT，3个条件满足其一就停止算法。

3 实验与结果分析

采用国内某电厂的实际数据来验证算法的有效性，选取其中160组数据进行实验。计算机硬件配置：CPU T5870 2.00GHz，内存1.96GByte。相关算法程序采用VC++6.0编写。算法参数设定：种群数NP为50个，种群粒子维数ND为2，算法最大循环次数NLOOP为1 000，最优解最大不更新次数NNF为20，算法最大运行时间NMAXT为30min。实验用不同算法对相同时间段内的锅炉烟气含氧量进行软测量，结果与误差如图3、4所示。

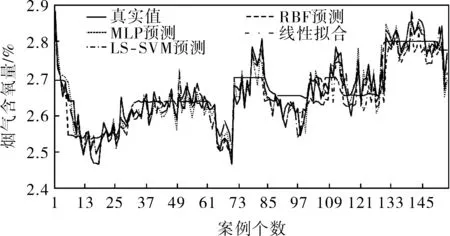
图3 不同算法烟气含氧量软测量结果

图4 不同算法的预测误差绝对值

由图3可以看出，笔者提出的软测量方法与其他算法对比，均能较好地跟随烟气含氧量的变化，反映其变化趋势；由图4可以看出，笔者所提算法与其他算法相对比，其最大测量误差绝对值低于0.07，相对误差低于3%，满足实际生产需要。

4 结束语

针对电厂锅炉烟气含氧量测量过程中存在的成本高及测量数据传输延迟等问题，结合机理分析和数据相关性分析选定影响因素，设计基于差分进化算法的自校正最小二乘支持向量机算法，用某电厂锅炉的实际数据进行的实验结果表明：该算法与其他算法相对比，其最大测量误差绝对值低于0.07，相对误差低于3%，满足实际需要，能够为锅炉生产的顺利进行提供必要参考。

[1] 范晗东,彭鑫,吕玉坤.基于烟气含氧量的电站锅炉经济性优化分析研究[J].电力科学与工程,2009,25(12):40～45.

[2] 周建新,樊征兵,司风琪,等.电站锅炉燃烧优化技术研究发展综述[J].锅炉技术,2008,39(5):33～36.

[3] 田亮,霍秋宝,刘鑫屏,等.电站锅炉总风量软测量[J].中国电机工程学报,2014,34(8):1261～1267.

[4] 卢洪波,王金龙.基于LIBSVM和智能算法的电站锅炉飞灰含碳量优化[J].东北电力大学学报,2014,34(1):16～20.

[5] 卞和营,王军敏.支持向量回归在飞灰含碳量软测量中的应用[J].计算机测量与控制,2014,22(2):345～348.

[6] 李少华,许乐飞,宋东辉,等.基于BP神经网络的锅炉烟气中的CO的测量[J].东北电力大学学报,2014,34(3):85～88.

[7] 湛腾西,郭观七.电厂烟气含氧量的智能混合预测方法[J].仪器仪表学报,2010,31(8):1826～1833.

[8] 袁俊文,周正兴,王丽,等.基于改进BP神经网络的烟气含氧量软测量方法[J].黑龙江电力,2011,33(6):418～420.

[9] 韩璞,王东风,翟永杰.基于神经网络的火电厂烟气含氧量软测量[J].信息与控制,2001,30(2):189～192.

[10] 王刚,刘林,王朋.基于微分进化和SMO算法的烟气含氧量软测量[J].电力科学与工程,2012,28(2):71～74.

[11] 刘长良,李淑娜.基于LS-SVM和单纯形的烟气含氧量软测量[J].热能动力工程,2010,25(3):292～296.

[12] 许巧玲,林伟豪,赵超,等.基于KPCA-LS-SVM的工业锅炉烟气含氧量预测[J].计算机与应用化学,2012,29(7):834～838.

[13] 张倩,杨耀权.基于支持向量机回归的火电厂烟气含氧量软测量[J].信息与控制,2013,42(2):258～263,272.

[14] 周霞,柳善建.基于多目标LSSVM回归的火电厂烟气含氧量软测量[J].计算机测量与控制,2014,22(10):3101～3104.