基于自适应学习速率的模糊神经网络控制器

邹彦艳 孙 晶 邵克勇 李征璐

(东北石油大学电气信息工程学院,黑龙江 大庆 163318)

在实际工业生产现场中有很多复杂的控制系统，它们通常具有大惯性、非线性及时间延迟等特性，很难通过精确的数学模型来表示系统的受控对象，而模糊控制具有不依靠模型及适应能力强等特点，因此可将其应用到有复杂控制系统的实际生产中。

随着模糊控制越来越广泛的应用，一些学者开始通过采用多种算法(如神经网络等)与模糊控制相结合[1]，来得到适用性更强的新控制算法。张秀玲等提出了一种优化自适应模糊神经网络算法，并应用在污水处理系统中，提高了系统的稳定性，使模糊神经网络具有更高的鲁棒性[2]。赵继印等提出一种基于误差自动调节修正因子的自适应学习速率法，从而提高网络的收敛速度[3]。徐春梅等提出的权矩阵学习速率自适应调整算法，可以取得更好的控制跟踪效果[4]。房振勇等通过调节动量因子实现学习速率的自调节，提高了学习的平稳性[5]。王玲芝和王忠民将BP网络的节点实际输出与期望输出的平均绝对值误差及其误差变化率作为自变量，并寻求学习速率与两个自变量的函数关系，对学习速率进行了动态调整，使系统具有更快的收敛速度[6]。徐雅斌和杜鹏将模糊推理方法引入到BP算法中，实现了自适应调节学习速率[7]。

在此，笔者将带有动量因子的自适应学习速率的新型BP算法应用到模糊神经网络控制器中，给出了一种基于自适应学习速率的模糊神经网络控制器，利用新型BP算法来训练模糊控制中的隶属度函数和模糊规则，采用模糊推理的方法来自适应调节学习速率，使系统具有良好的控制效果。

1 问题描述①

考虑如图1所示的模糊神经网络[8]，该网络为五层结构，其输入为误差e和误差变化ec，输出为u。

图1 模糊神经网络结构

设系统的理想输出为yd，实际输出为y，则性能指标J的计算式为[9]：

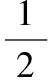
通常，模糊神经网络控制器中学习速率是常数，在学习过程中很难确定一个最佳学习速率，同时在修正权值、中心值和宽度值时，仅按当前时刻的负梯度方向修正，而不考虑以前时刻的梯度方向，会导致在学习过程中出现振荡和收敛速度慢的问题。

2 基于自适应学习速率的模糊神经网络控制器

2.1 参数初始化

通常，初始权值、隶属度函数的中心值和宽度值会取常数或赋一个较小的随机数，但这种初始化方法会导致网络收敛速度较慢，甚至只能收敛到局部极值上。因此，笔者采用均匀分布随机数产生权值、中心值和宽度值，使初始权值随机产生并均匀分布。

2.2 带动量因子的BP改进算法

在标准的BP算法中，设η是学习速率，模糊神经网络控制器中的可调参数权值ωij、中心值mij和宽度值σij的计算式分别为：

在此，引入动量因子β(0≤β<1)，采用上一次在学习过程中的校正量来影响本次的校正量，以加快收敛速度，即:

通过选择合适的β值，可避免每一步修正值过大出现的振荡现象或因BP陷入局部最小值和修正值过小的问题。

2.3 自适应学习速率

由可调参数知，学习速率通常是设定的常数，但在整个过程中，无法找到一个最合适的学习速率来满足该算法对学习速度的要求。为此，通常采用自适应调节学习速率的方法[10]，即根据实际情况和网络误差来自适应调节：

其中，Et为t时刻的误差，Et+1为(t+1)时刻的误差。可见，若误差变化修正方向正确，即总误差减小，则学习速率增大；反之，则学习速率减小。α通常取0.01～0.03，虽然采用这种方法对于缩短学习时间、提高收敛速度有一定的效果，但α仍然是一个常数，学习速率依然是一个不变量。因此，对于学习速率的问题仍然需要研究，笔者采用模糊神经网络自调整学习速率的方法，以提高系统的收敛性。

将误差E总和误差变化ΔE看作模糊程度，从而引入模糊推理的概念，按照E总→0和ΔE→0的程度来更新学习速率。具体步骤如下：

a. 模糊化。求出y、E总和ΔE，并对E总和ΔE进行模糊化处理。

b. 模糊分割。将误差和误差变化分别分割为5个语言变量，分别为NB、NS、ZE、PS和PB；将学习速率分割为5个语言变量，分别为ZE、PS、S、B和PB。

e. 清晰化。采用加权平均法，使清晰化后的η用于BP算法中的误差反传。

表1 学习速率η的模糊控制规则

因此，采用模糊推理的方法来自调整学习速率，使学习速率在学习过程中适时地改变，从而提高控制系统的收敛速度。

考虑如下线性系统：

(1)

e=yd-y

(2)

(3)

控制器的输出ui为：

ω——权值；

φ——第三层的输出。

因此可以得到：

(4)

φ=[φ1…φNrφ1x1…φNrx1…φ1xNi…φNrxNi]T

取Ni=2，Nr=7。

理想控制器的输出u*为：

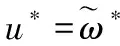
(5)

将式(5)代入式(1)得：

(6)

将式(1)和式(6)作差，并将式(2)、(3)代入其中，得到系统的误差方程为：

(7)

将式(4)、(5)代入式(7)可得：

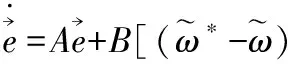
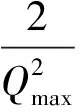
证明P是对称正定矩阵，它满足ATP+PA=-Q，其中Q是可选的对称正定矩阵。

又：

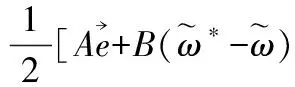
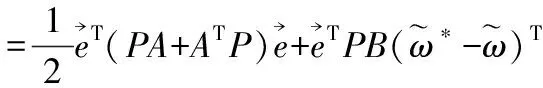
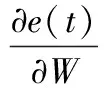
式中O(t)——模糊神经网络的实际输出；

W——m、σ、ω的统称。

定义：

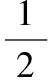
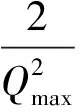
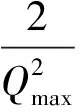
3 仿真实验与分析

考虑如下二阶控制系统：

采样时间T=1ms，产生49条规则，阶跃输入信号r=1.0、β=0.75，经过500次迭代，初始权值取[0,1]上的均匀随机数，初始中心值是[1.0,1.6]上的均匀随机数，初始宽度值是[2.0,2.6]上的均匀随机数。

对于同一受控对象，运用Matlab进行仿真，对比并分析本方法、模糊控制和常规模糊神经网络控制方法的仿真实验结果(图2、3)。采用本文方法得到的学习速率变化曲线如图4所示。

图2 系统的输出对比

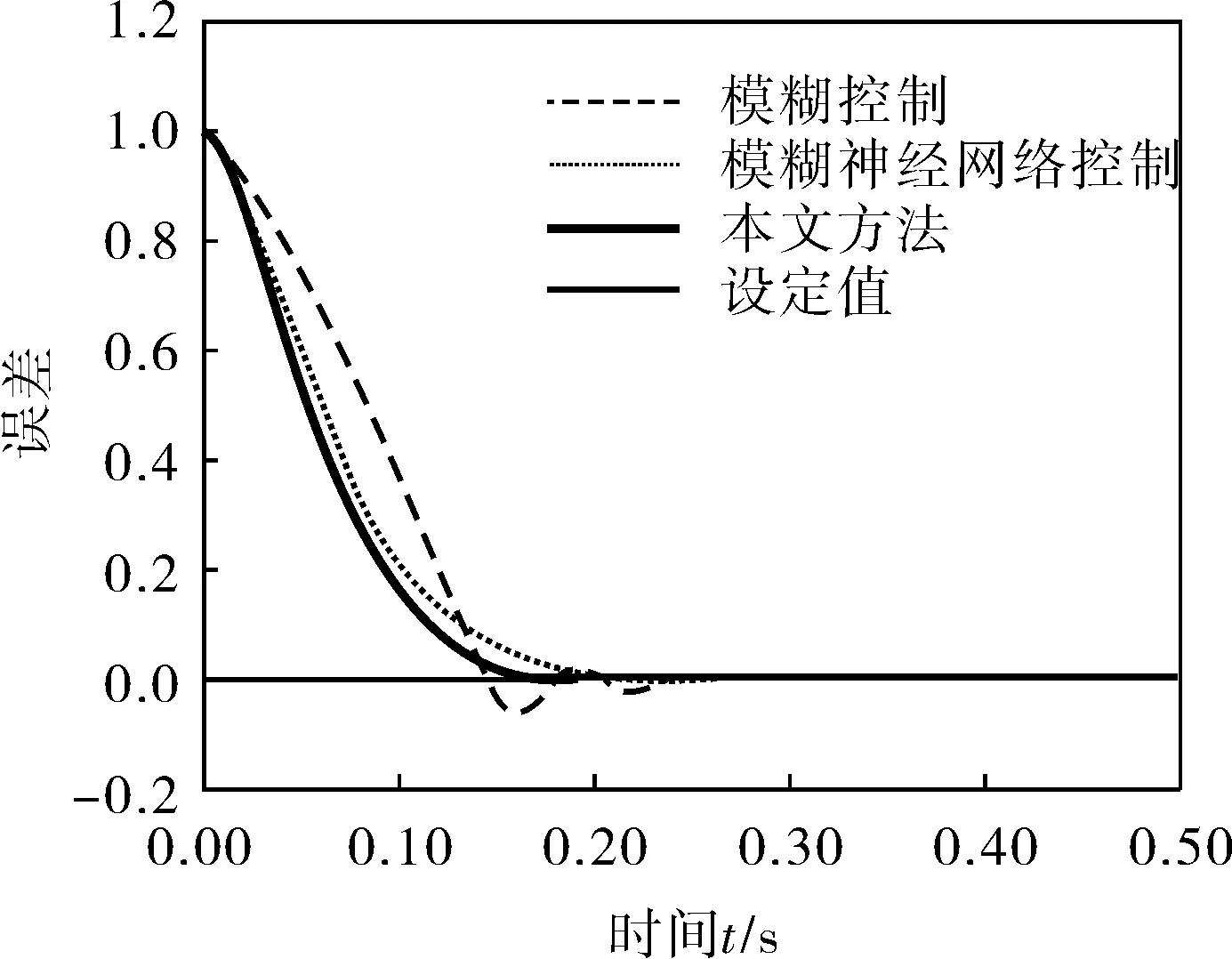
图3 系统的误差对比

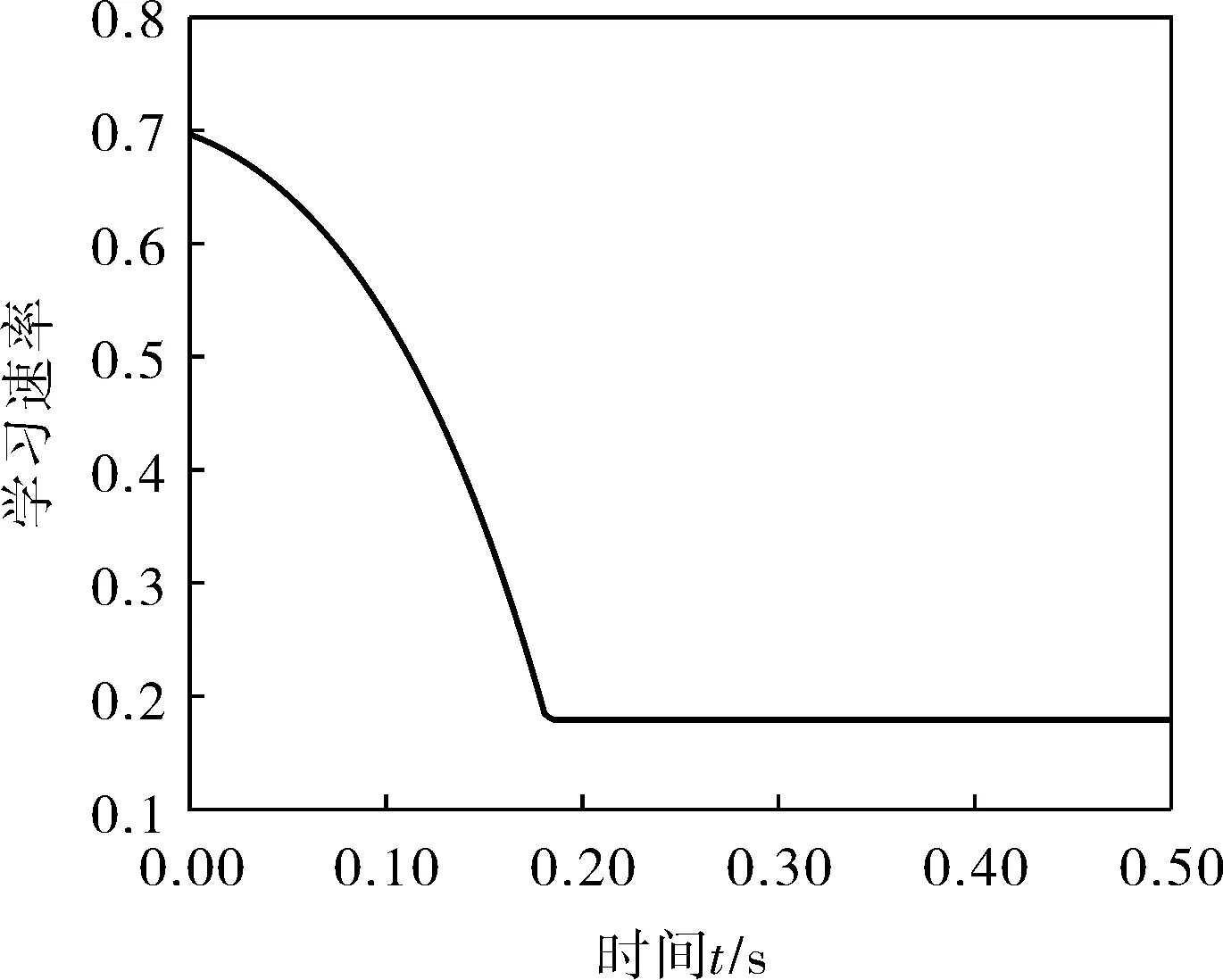
图4 学习速率变化曲线

实验对比结果见表2。

表2 实验对比结果

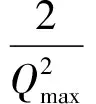
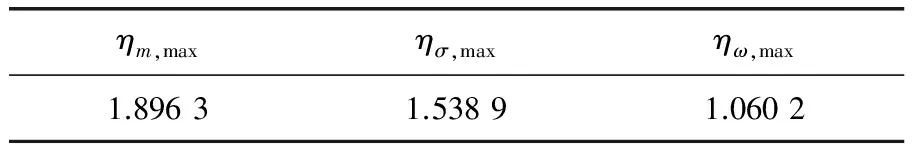
表3 学习速率满足系统收敛性的最大值

综上所述，本文方法调整时间短、响应速度快、精确度高，能达到较好的控制水平和控制效果。

4 结束语

笔者提出了一种新型的BP算法，将带有动量因子的自适应学习速率的BP算法引入模糊神经网络控制器中。利用模糊推理方法，实现了学习速率的自适应调节，选择合适的动量因子可加快学习过程中的收敛速度，并通过Lyapunov定理证明了系统的稳定性。仿真结果表明，笔者提出的方法可以提高系统的控制性能，使系统达到较好的控制水平。

[1] 高润泉,杨志成,王宏,等.模糊神经网络控制在二阶液位控制中的应用[J].化工自动化及仪表,2008,35(2):75～77.

[2] 张秀玲,郑翠翠,黄兴格,等.基于参数优化的自适应模糊神经网络控制在污水处理中的应用[J].化工自动化及仪表,2009,36(3):12～14.

[3] 赵继印,李建坡,郑蕊蕊.自适应学习速率法在变压器故障诊断中的应用[J].吉林大学学报(信息科学版),2008,26(4):415～420.

[4] 徐春梅,尔联洁,刘金琨.动态模糊神经网络及其快速自调整学习算法[J].控制与决策,2005,20(2):226～229.

[5] 房振勇,游文虎,冯汝鹏.改进BP算法在模糊神经网络中的应用[J].北京航空航天大学学报,2007,33(11):1321～1324.

[6] 王玲芝,王忠民.动态调整学习速率的BP改进算法[J].计算机应用,2009,29(7):1894～1896.

[7] 徐雅斌,杜鹏.基于隶属度函数的BP人工神经网络改进算法[J].辽宁工程技术大学学报(自然科学版),2009,28(5):795～797.

[8] Yu W,Li X O.Fuzzy Identification Using Fuzzy Neural Networks with Stable Learning Algorithms[J].IEEE Transactions on Fuzzy Systems,2004,12(3):411～420.

[9] 牛培峰,郭兴华,孟凡东.模糊神经网络控制在汽温系统中的应用[J].控制工程,2010,17(3):293～296.

[10] 李义宝,张学勇,马建国,等.基于BP神经网络的改进算法研究[J].合肥工业大学学报(自然科学版),2005,28(6):668～671.