短幅内摆线型螺杆-衬套副滑动速度分析*
2015-01-13杜秀华刘双新宋玉杰韩国有
杜秀华 刘双新 宋玉杰 韩国有
(东北石油大学机械科学与工程学院)
单螺杆式水力机械是石油化工和钻采机械领域中常用的水力机械,如单螺杆泵、单螺杆钻具及单螺杆油气混输泵等。它们都是依靠一对螺杆-衬套副的啮合来实现液体传输或动力传递的,因此螺杆-衬套副的滑动速度是影响其磨损程度和使用寿命的重要因素之一。早在20世纪80年代苏义脑等就对短幅内外摆线型螺杆-衬套副的线型理论进行了系统的研究,形成了螺杆-衬套副线型的基本理论[1~3]。20世纪90年代万邦烈等通过理论和试验方法研究了螺杆-衬套副的啮合理论与优化设计方法[4~6]。2000年以后许多学者进行了螺杆-衬套副的运动仿真和有限元计算,并取得了一定的成果[7~9],但对螺杆-衬套副运动学方面的研究仅限于对结构简单的单头普通内摆线型螺杆-衬套副螺杆在衬套内的运动轨迹和运动规律进行分析,针对螺杆-衬套副滑动速度的研究尚无报道,为此笔者对多头短幅内摆线型螺杆-衬套副的线型设计、运动分析和滑动速度的计算方法进行系统的研究。
1 螺杆-衬套副的线型设计
螺杆-衬套副的空间共轭问题可转化为平面共轭曲线副的相对运动问题[10],因此对螺杆-衬套副的啮合状况和运动分析可集中在其横截面上。螺杆和衬套的横截面曲线简称线型或型线。短幅内摆线型螺杆-衬套副的线型设计首先形成一条短幅内摆线作为衬套骨线,再利用外滚法形成螺杆骨线,最后分别向外侧取骨线的等距线,形成螺杆-衬套副的线型。
首先采用无包心法形成Nw头的短幅内摆线作为衬套骨线R(θ),其复矢量方程为[10]:
R(θ)=R2(Nejθ+Ke-jNθ)
(1)
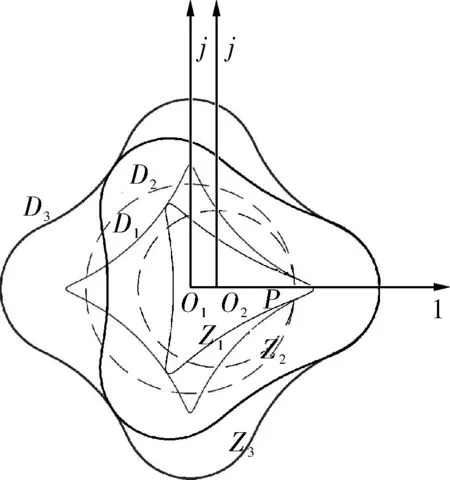
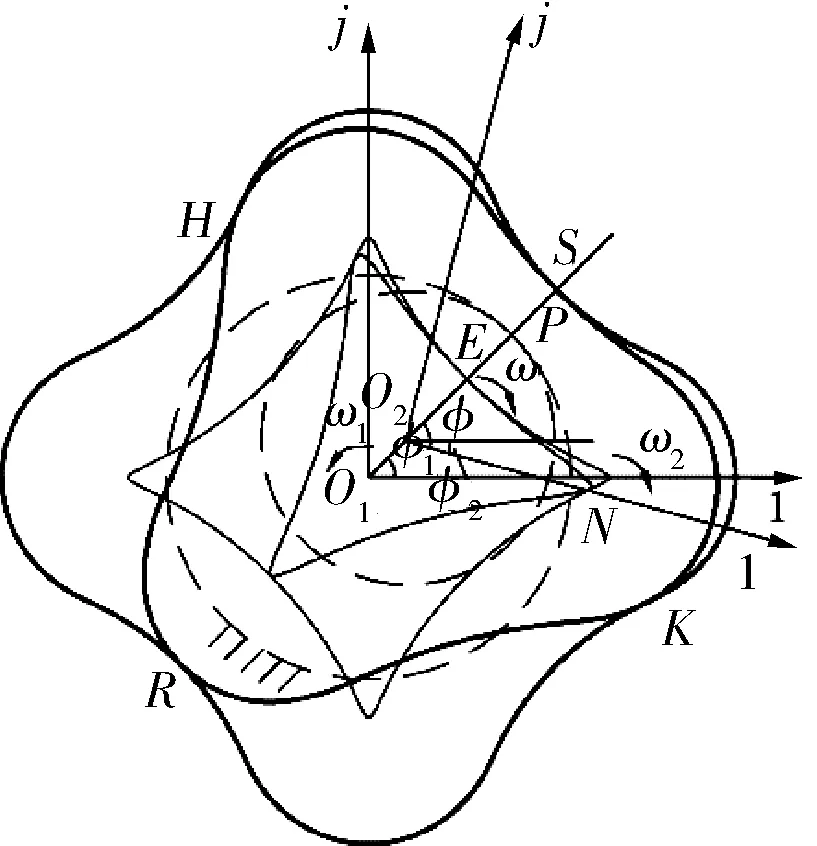
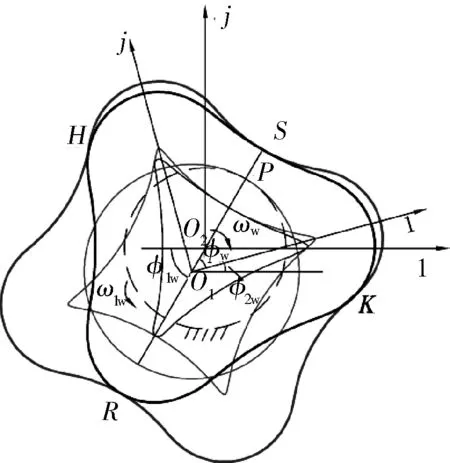
式中K——变幅系数,0 N——螺杆头数,N=Nw-1; R2——滚圆半径,mm; θ——导圆滚角,0≤θ≤2π。 形成短幅内摆线的导圆半径R1与滚圆半径R2的关系为: R1=NwR2 (2) 再采用外滚法,即以R(θ)的包心法导圆做动瞬心圆,携带R(θ)沿定瞬心圆外侧做纯滚动,R(θ)运动轨迹的内包络线即为螺杆骨线,如图1所示,其中动瞬心圆半径R″与定瞬心圆半径R′分别为: R″=NwKR2 (3) R′=NKR2 (4) 图1 外滚法形成螺杆骨线 因此动瞬心圆与定瞬心圆的偏心距E(即螺杆-衬套副的偏心距)为: E=R″-R′=KR2 (5) 综上,只要给定短幅内摆线型螺杆-衬套副的基本结构参数,即螺杆头数N、偏心距E和变幅系数K,就可确定螺杆-衬套副的骨线,并满足共轭条件。再给出等距半径或等距半径系数,则可设计出螺杆-衬套副的线型。 螺杆-衬套副的结构参数为:短幅内摆线型,变幅系数K=0.8,偏心距E=5mm,螺杆头数N=3,等距半径系数r0=2。根据上述线型设计方法得出螺杆-衬套副的线型如图2所示。图中曲线Z1、Z2、Z3分别表示螺杆的骨线、定瞬心圆和线型,曲线D1、D2、D3分别表示衬套的骨线、动瞬心圆和线型。为方便分析,在图2中建立两个复平面参考坐标系,其中1-O1-j的原点位于衬套型线的几何中心,且与衬套固连,为静坐标系;1-O2-j的原点位于螺杆型线的几何中心上,且与螺杆固连,为动坐标系。 图2 螺杆-衬套副啮合的初始状态 单螺杆式水力机械工作时一般螺杆旋转,衬套不动,即定瞬心圆携带螺杆骨线和型线在动瞬心圆内做纯滚动,称为第一种啮合运动,它可分解为两种运动(图3): a. 螺杆中心O2绕衬套中心O1做半径为E的公转,公转角为φ1,公转角速度为ω1,方向逆时针,螺杆的滚角为φ,滚角速度为ω,方向顺时针,公转角与滚角的关系为φ1=-Nφ/(N+1); b. 螺杆绕自身中心O2做自转,自转角φ2为公转角与滚角的代数和,自转角速度为ω2,方向为顺时针,即φ2=φ/(N+1)。 图3 第一种啮合运动时间t时的啮合状态 螺杆-衬套副在啮合过程中,螺杆骨线上的3个尖点将依次连续地划过衬套骨线,这3个接触点相对于螺杆来说是固定的,称为固定接触点(如点N);螺杆与衬套骨线间还有一个接触点(E点),它沿衬套边界逆时针流动,称为流动接触点。与螺杆骨线尖点对应的一段型线(圆弧),即螺杆的齿凸,其上的各点将依次与衬套型线接触,因此对于型线来说,不存在固定接触点,但流动接触点仍然存在。为叙述问题方便,将型线的这两类接触点称为螺杆齿凸接触点(H、K、R点)和螺杆齿凹接触点(S点),简称为齿凸接触点和齿凹接触点。 当φ>0的瞬时,螺杆齿凸与衬套齿凹由线接触变为点接触,螺杆的速度瞬心P沿定瞬心圆逆时针移动,而齿凸接触点K(还有H、R)沿衬套轮廓顺时针移动,齿凹接触点S沿衬套轮廓逆时针移动;φ由0增大到π的过程中,瞬心到齿凸接触点的距离PK逐渐增大到最大值;φ由π增大到2π的过程中,PK逐渐减小,直到螺杆齿凸又一次与衬套的下一个齿凹变为线接触,完成螺杆与衬套啮合的一个周期。由此可见,螺杆和衬套要完成一个循环的啮合,螺杆导圆的滚角应为(N+1)2π。 3.1齿凸接触点的滑动速度 外滚法形成螺杆-衬套副时相当于螺杆不动,衬套做行星运动,称为第二种啮合运动,它可分解为两种运动(图4): a. 衬套中心O1绕螺杆中心O2做半径为E的公转,公转角φ1w,公转角速度ω1w,方向为逆时针,衬套的滚角φw,滚角速度为ωw,方向为顺时针,衬套的公转角与滚角的关系为φ1w=-Nwφ/(Nw-1); b. 衬套绕自身中心O1自转,自转角φ2w为公转角与滚角的代数和,自转角速度为ω2w,方向仍为逆时针,即φ2w=-φw/(Nw-1)。 图4 第二种啮合运动时间t时的啮合状态 单螺杆式水力机械一般是螺杆旋转,衬套不动,因此为了方便利用短幅内摆线型理论推导螺杆-衬套副的滑动速度,则要推出两种啮合运动的参数关系。图3、4表示的是利用两种运动形式达到相同啮合状态,由啮合原理不难得到关系式φw=-φ1,φ1w=-φ,φ2w=-φ2。 由图3可知,齿凸接触点(如K点)的相对滑动速度Vt的表达式为: Vt=PK×ω2 (6) 由几何矢量关系得: PK=O1K-O1P (7) O1K=O1N+NK (8) 则: Vt=(O1N+NK-O1P)ω2 (9) 其中,O1N为固定接触点N在静坐标系1-O1-j中的运动轨迹,即定子骨线;NK为等距半径矢量;O1P为衬套导圆半径矢量。 θ角和滚角φ的关系由短幅内摆线型固定接触点的φ函数确定,φ函数为[10]: φw=-Nθ+2Tπ,0<θ<2π,T=0,1,2,…,N-1 (10) φw与固定接触点对应,若只考虑螺杆骨线第一个尖点的运动轨迹,令T=0,则: θ=-φw/N (11) 由此可知: θ=-φ/(N+1) (12) 固定接触点的运动轨迹即为衬套骨线,方向顺时针,则矢量方程为: R(θ)=R2(Ne-jθ+KejNθ) (13) 由此可知: (14) 等距半径矢量NK为: (15) (16) P点是两导圆做纯滚动时的速度瞬心,因此: O1P=R2(N+1)Kejφ1 (17) 结合上式,可得: (18) 整理得齿凸接触点的相对滑动速度为: (19) 式(19)中滚角φ为顺时针方向,为了在分析问题时,给φ代入正值,将φ前加上负号,式(19)变形为: (20) 将K=1分别代入式(20)、(16),整理后可得到普通内摆线型螺杆-衬套副间齿凸接触点的相对滑动速度为: (21) 3.2齿凹接触点的滑动速度 螺杆-衬套副在啮合过程中,齿凹接触点只有一个(S点),如图3所示。该点的滑动速度Va表示为: Va=PS×ω2 (22) 由几何矢量关系得: PS=O1E+ES-O1P (23) 其中,O1E为螺杆骨线流动接触点在静坐标系1-O1-j中的运动轨迹;ES为等距半径矢量。 螺杆骨线流动接触点的运动轨迹即衬套骨线,方向逆时针,则有: (24) 等距半径矢量: ES=R2r0ejα=rejα (25) (26) 其中,α表达式前的正负号依据具体情况而定,应遵循等距向量朝外的原则。 θ和滚角φ的关系由短幅内摆线型流动接触点的φ函数确定,φ函数为[10]: φw=-Nθ+2β+2Tπ,0≤θ<2π,T=0,1,2,…,N-1 (27) (28) 整理式(27)、(28),并取T=0(只分析第一头)得: Nφ/(N+1)=-Nθ+2β (29) (30) 由此可见,θ与φ之间无法用初等函数来表达,只能利用数值分析方法,绘制φ曲线接触图,进而分析确定θ与φ的数值关系。 将式(18)、(24)、(25)分别代入式(22)、(23)得齿凹接触点的滑动速度为: (31) 式中的α和θ由式(26)、(29)、(30)确定,都用滚角φ表达。 将K=1代入式(26)、(30)并利用三角函数变换,得: α=±(π/2)-(N-1)θ/2 (32) β=(N+1)θ/2 (33) 将式(33)代入式(29)得φ与θ的关系为: θ=-Nφ/(N+1) (34) 将式(32)、(34)代入式(31)得到普通内摆线型螺杆-衬套副齿凹接触点的滑动速度为: (35) φ角为顺时针,为了在分析问题时,给φ代入正值,则在φ前加上负号,则公式(35)变形为: (36) 4头普通内摆线型螺杆-衬套副,设其偏心距E=10mm,等距半径系数r0=1,自转角速度ω2=π/10rad·s-1,滚角速度ω=π/2rad·s-1,公转角速度ω1=2π/5rad·s-1。将数据分别代入式(21)、(36),并将滚角φ用时间t表示(φ=ωt)得: (37) (38) 利用MATLAB软件将式(37)、(38)生成曲线如图5、6所示。 图5 齿凸接触点的滑动速度曲线 图6 齿凹接触点的滑动速度曲线 由曲线可知,齿凸接触点的滑动速度在衬套内凹处最小,在衬套内凸中点处最大;齿凹接触点的滑动速度在离开衬套内凹处的瞬间最大,在衬套内凸中点最小;齿凹接触点的滑动速度的最大值是齿凸接触点的滑动速度的最小值;齿凸接触点的啮合周期是齿凹接触点的N倍。 5.1单螺杆式水力机械中螺杆-衬套副的线型形成原理和过程较复杂,所涉及到的参数较多,分析确定了形成短幅内摆线型螺杆-衬套副线型所需的基本参数。 5.2分析了螺杆-衬套副的啮合过程与规律,定义了螺杆-衬套副骨线间的固定接触点和流动接触点,以及螺杆-衬套副型线间的齿凸接触点和齿凹接触点。 5.3推导出了短幅(普通)内摆线型螺杆-衬套副齿凸接触点和齿凹接触点的相对滑动速度公式,并通过具体应用得出了螺杆-衬套副在啮合过程中齿凸接触点和齿凹接触点滑动速度的变化规律。 [1] 苏义脑,谢竹庄.螺杆钻具马达线型分析基础及研究方法[J].石油钻采机械,1985,13(6):10~20. [2] 苏义脑,于炳忠,谢竹庄.单螺杆钻具马达线型分析[J].石油学报,1986,7(4):95~109. [3] 苏义脑,谢竹庄.单螺杆钻具马达短幅内摆线等距线型分析[J]. 石油机械,1987,15(6):5~11. [4] 万邦烈,曹玉德.短幅内摆线型单螺杆式水力机械螺杆- 衬套副的评价指标及参数的优选[J].石油矿场机械,1989,18(2):17~27. [5] 葛占玉,万邦烈.单头单螺杆式水力机械螺杆- 衬套副的啮合理论及其作用力[J].中国石油大学学报,1990,14(5):33~40. [6] 刘孟,万邦烈.单螺杆油气混输泵螺杆- 衬套副结构参数的优选[J].中国石油大学学报(自然科学版),1991,15(2):53~66. [7] 安永生,宋扬,张德实,等.螺杆泵转子三维运动仿真分析及线型优化设计[J]. 中国石油大学学报(自然科学版),2012,36(3):155~164. [8] 郭爽,付保军,刘建群.内摆线型单螺杆泵共轭副等距曲线运动分析[J].哈尔滨师范大学自然科学学报,2009,25(5):78~80. [9] 李晓明.单螺杆泵转子在定子衬套中运动接触迹的研究[J].机械工程及自动化,2007,143(4):58~60. [10] 苏义脑.螺杆钻具研究及应用[M].北京:石油工业出版社,2001:43~52,94~101.
2 螺杆-衬套副的运动分析
3 螺杆-衬套副滑动速度的计算方法


4 滑动速度计算公式的应用


5 结论
