矩形截面螺旋通道气液两相流可视化研究与压降计算

周云龙 李佳研

(东北电力大学能源与动力工程学院)

单螺杆膨胀机复杂三维矩形截面螺旋通道内多组分、多相流动结构是影响膨胀机效率的重要因素之一，而目前主要侧重于膨胀机的加工和性能研究[1]，缺乏对其内部多相流动结构和相分布规律的研究，开展这方面的研究具有重要意义。

目前，对于圆形截面螺旋通道内气(汽)水两相流动特性已有广泛的研究[2～5]，但对于其他截面形状的螺旋通道,大部分还停留在数值研究阶段[6],实验研究较少。而仅有的对于矩形截面螺旋通道的实验研究也多是针对单相流体所进行的流场结构和流动特性的研究，Bolinder C J和Sunden B对正方形截面螺旋通道内层流流场进行了测量[7]。张丽等对低雷诺数下高宽比为3.5的矩形螺旋通道流场进行了实验测量，测量值与数值模拟值吻合较好[8]。马源等利用二维粒子图像测速仪(PIV)对矩形截面螺旋通道的5个横截面流场进行了实验测量，获得了不同雷诺数下，不同横截面的二次流瞬态流场和涡量场图像[9]。但是，对矩形截面螺旋通道内气液两相流型和摩擦压降的研究还未见报道。

鉴于此，笔者通过实验的方法研究了单螺杆膨胀机内部矩形截面螺旋通道空气-水两相流的流型和摩擦压降，探究了流型对摩擦压降的影响规律，得出了适用于计算不同流型下摩擦压降的经验关系式。为寻求有效手段提高膨胀机效率，改善其性能提供必要的研究基础。

1 实验系统与装置

通道由一个外壁带螺旋翅片的圆柱和一个外套管围成，为了实现可视化研究，材料采用有机玻璃，螺旋翅片由车刀车出，与外套管的配合公差小于1mm。外套管内径120mm、厚5mm，翅片高22mm，螺旋翅片厚度6mm，螺距110mm。所围成的矩形截面的长、宽分别为24、22mm。通道当量直径为23mm，曲率为0.47，挠率为0.36，Bolinder C J认为在2.5倍螺距处，流体流动已经充分发展[10]。因此为保证流动充分发展，本实验中，取有效直管段的长度为550mm，即5倍螺距。

实验装置流程如图1所示。水和空气分别在离心式水泵和空气压缩机的动力推动下流经电磁流量计和热式气体质量流量计，经两相混合器充分混合后流入实验段，而后经旋风分离器分离，水流回水箱继续循环使用，空气排入大气中。空气压缩机额定工作压力为0.8MPa，实验过程在常温下进行，压力参数范围为0.1～0.3MPa；空气的折算速度范围为0.2～20.0m/s；水的折算速度范围为0.04～2.70m/s。

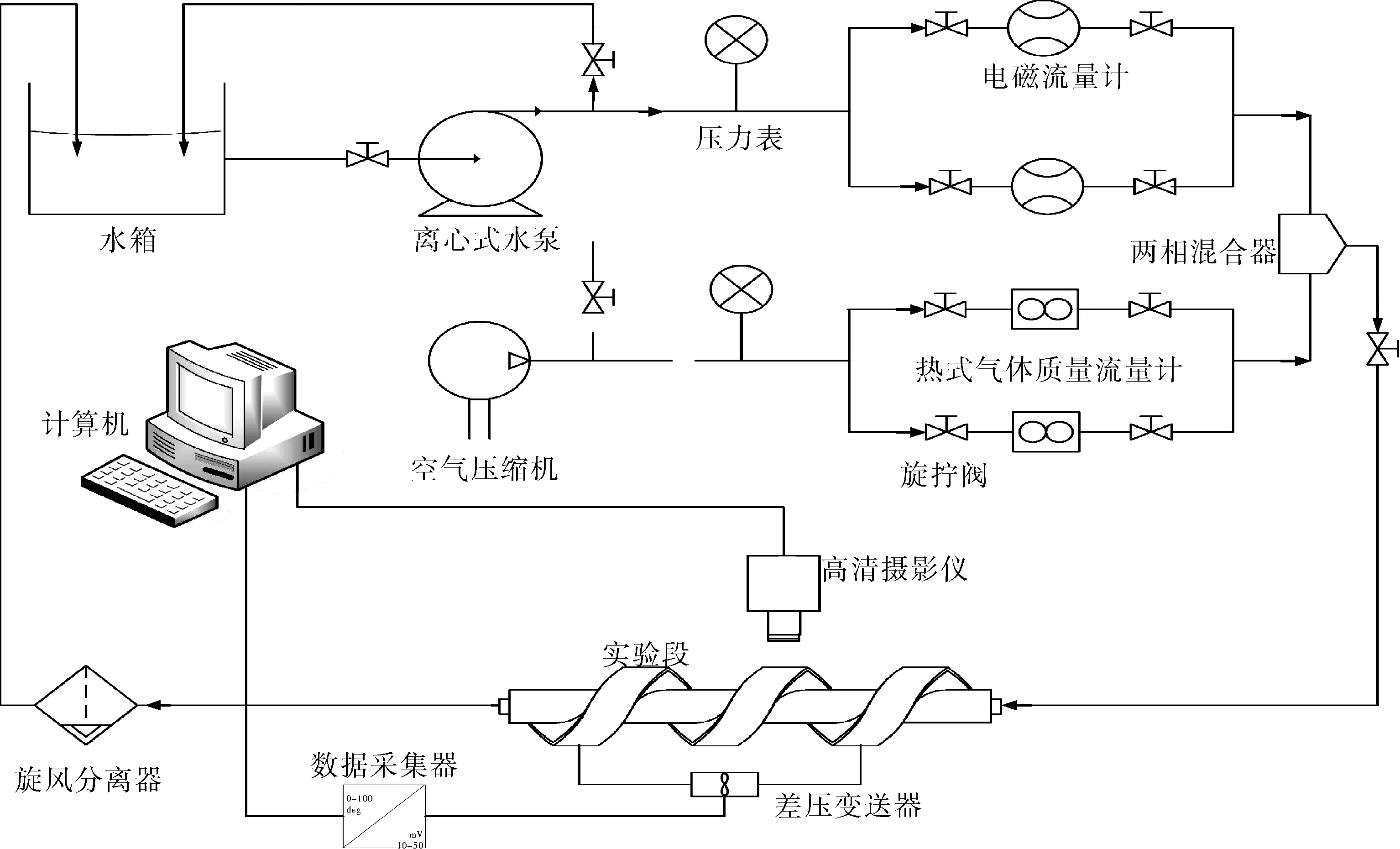
图1 实验系统示意图

实验所使用的高速摄影仪镜头水平放置并与实验段中轴线处于同一水平面上，拍摄实验段前侧的流动图像，其最大分辨率为1536×1024，最大帧频可达到10 000帧/s，可以十分清晰地拍摄到通道内的气液两相流型的变化。光源采用6 400K色温的三基色照明，光亮稳定、均匀，无闪烁。使用差压变送器采集机压差信号通过数据采集器输入计算机，实验选择相距2倍螺距的两个取压点采集压差信号，两点在同一水平线上，首个取压点距离进口2.5倍螺距。实验中采用的差压变送器在实验前使用电子手操器进行量程校准。

2 实验结果与分析

2.1矩形截面螺旋通道两相流流型

通过高速摄影仪观察了矩形截面螺旋通道内的流型。对实验拍得的图片进行整理分析后，笔者将矩形截面螺旋通道气、液两相流流型区分为4种：柱塞状流、弹状流、环状流和分散泡状流，并绘制了流型图。

当气相与液相折算速度均较小时，观察到了柱塞状流，气相以长气泡状分散在连续的液相中，如图2a所示；随着气相折算速度的增高，观察到了弹状流的存在，如图2b所示，大气泡呈现气弹状，其间伴有小气泡产生；随着气相折算速度的继续增高，管道内逐渐形成了环状流流型，气相在管内中心流动，形成气柱，液相趋于贴近壁面四周流动，如图2c所示；当液相折算速度增高到一定程度时，观察到了分散泡状流流型，如图2d，气相变成细微小气泡分散在连续的液相中。

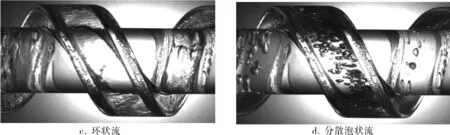
图2 典型流型

依据实验数据并借助观察所得将矩形截面螺旋通道试验结果绘制成流型图，如图3所示。从流型图可以看出：与经典圆形截面螺旋管的流型图[11]相比，各流型转换的过渡区域的边界形状基本一致，只是转换边界过渡区的位置有一定差异，不同之处是本次实验未发现在圆形截面螺旋管一定区域内会出现的波状分层流型，原因有待继续研究；柱塞状流向弹状流转换和弹状流向环状流转换的过渡边界为一近似垂直的带状区域，过渡区流型如图4a、b所示，过渡区气相折算速度分别为JG=0.81～1.12m/s、JG=16.8～20.1m/s。如果把柱塞状流和弹状流看作统一的间歇流，那么间歇流与分散泡状流转换的过渡边界类似一倾斜上升的带状区域，过渡区流型如图4c所示，过渡区液相折算速度约为JL=0.73～1.19m/s。

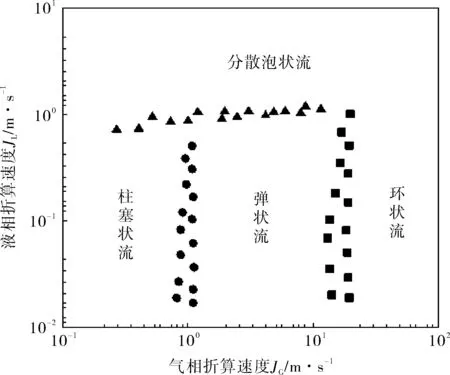
图3 流型

图4 过渡区流型

气液两相流各种流型的出现及其转换是由作用在气液两相上的各种力的相互作用及平衡引起的[12,13]。水平管中，两相流主要受液相紊流应力和气相惯性力的作用，而在矩形截面螺旋通道中还要受到液相离心力的影响。间歇流向环状流的转换主要是由于气相流速的增加使气相惯性力增大，气相能够克服液相重力的作用并形成气柱，表面张力亦起到一定的作用；间歇流向分散泡状流的转换是由于当液相的流速比较高时，矩形截面螺旋通道内产生比较强烈的二次流，促使气液两相混合，当混合的趋势足以克服由液相离心力带来的两相分离趋势时，间歇流就会向分散泡状流转换。

2.2矩形截面螺旋通道摩擦压降

压差传感器测得的压降值为摩擦压降，即流动加速引起的压降与重力势差引起的压降之和，因此摩擦压降需要通过计算获得。 流动总压降的表达式为：

Δptotal=Δpstatic+Δpmom+Δpfrict

(1)

其中，Δptotal为管内流动总压降，Δpstatic为重力势差引起的压降(本实验中两取压点水平高度相同，Δpstatic=0)，Δpmom为管内流体加速引起的压降，Δpfrict为流体的摩擦压降，本次实验加速压降产生的影响较小，可以近似忽略，因此本实验系统的摩擦压降Δpfrict可以近似的等同于总压降Δptotal，进而通过实验测得。

2.2.1计算方法

笔者采用Lockhart- Martinelli分相模型处理实验数据，并使用Chisholm的B系数法拟合经验关系式，Lockhart- Martinelli分相模型是最早提出并被广泛应用至今的摩擦压降计算方法。具体计算式如下：

(2)

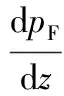
(3)

(4)

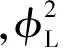
Chisholm在L- M实验曲线拟合式的基础上，进一步扩展数据范围，得到了经验式为：

(5)

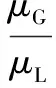
式中B——与工质物性及质量流速有关的参数；

n——雷诺数的指数值。

2.2.2计算结果与实验结果的比较

运用上述计算方法计算矩形截面螺旋通道的摩擦压降。通过与实验数据比较发现处理结果不够理想，与实验值有一定的偏差。从图5中可以看出：3种流型液相摩擦因子的分布并不一致，变化规律也不相同，这说明流型很大程度上制约着两相摩擦阻力。因此，为了提高摩擦压降计算模型预测的准确性，笔者采用了分流型计算矩形截面螺旋通道摩擦压降的方法。通过对摩擦压降的测量结果进行数学回归与处理，建立了适用于矩形截面螺旋通道不同流型下的摩擦压降计算经验关系式：

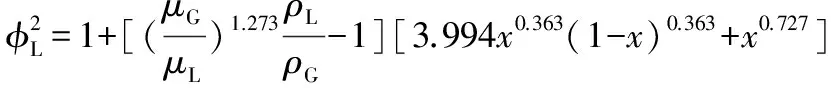
(6)

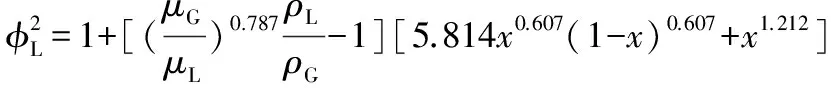
(7)

(8)

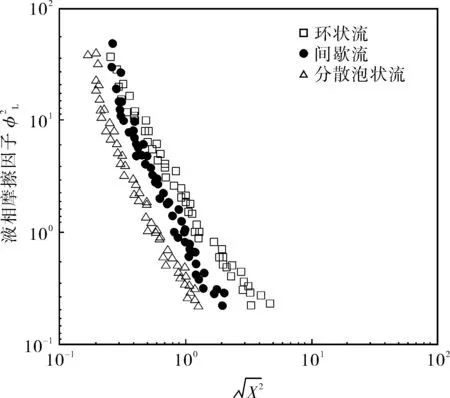
图5 3种流型的实验结果

图6为各流型下液相摩擦因子预测值与实验值的对比。3种流型(间歇流、环状流、分散泡状流)计算值与实验值的平均偏差分别为17.27%、13.73%、45.81%。间歇流与环状流的预测结果与实验值的平均偏差在30%以内，由文献[18，19]可知，计算结果与实验结果符合较好，而分散泡状流预测值与实验值的平均偏差为45.81%，总体上偏差较大。结果表明：Chisholm模型更适用于间歇流和环状流状态下的压降预测，而对于液相流速相对较高的分散泡状流区间的预测存在较大误差。

3 结束语

图6 液相摩擦因子预测值与实验值的对比

实验观察到了矩形截面螺旋通道气、液两相流有柱塞状流、弹状流、分散泡状流、环状流几种典型的流型，与经典圆形截面螺旋管的流型图相比，各流型转换的过渡区域的边界形状基本一致，只是转换边界过渡区的位置有一定差异，实验中未发现在圆形截面螺旋管一定区域内出现的波状分层流型。流型很大程度上制约着矩形截面螺旋通道内两相摩擦阻力，采用分流型计算矩形截面螺旋通道摩擦压降的方法可以有效提高预测精度。Chisholm模型适用于间歇流和环状流状态下的压降预测，分散泡状流状态下的压降预测有待进一步研究。

[1] 何为，吴玉庭，马重芳.两级单螺杆膨胀机空气动力系统性能研究[J].机械工程学报，2010，46(10)：139～145.

[2] Biswas A B，Das S K.Frictional Pressure Drop of Air Non- newtonian Liquid Flow Through[J].The Canadian Journal of Chemical Engineering，2007，85(2)：129～136.

[3] Biswas A B，Das S K.Two- phase Frictional Pressure Drop of Gasnon- Newtonian Liquid Flow Through Helical Coils in Vertical Orientation[J].Chemical Engineering and Processing：Process Intensification，2008，47(5)：816～826.

[4] Santini L，Cioncolini A，Lombardi C，et al. Two- phase Pressure Drops in a Helically Coiled Steam Generator[J]. International Journal of Heat and Mass Transfer，2008，51(19/20)：4926～4939.

[5] Murai Y，Yoshikawa S，Toda S，et al. Structure of Air- Water Two- phase Flow in Helically Coiled Tubes[J].Nuclear Engineering and Design，2006，236(1)：94～106.

[6] Xia G D，Liu X F，Zhai Y L，et al.Single- phase and Two- phase Flows Through Helical Rectangular Channels in Single Screw Expander Prototype[J].Journal of Hydrodynamics，2014，26(1)：114～121.

[7] Bolinder C J，Sunden B.Numerical Prediction of Laminar Flow and Forced Convective Heat Transfer in a Helical Square Duct with a Finite Pitch[J].International Journal of Heat Mass Transfer，1996，39(15)：3101～3115.

[8] 张丽，邢彦伟，吴剑华.矩形截面螺旋通道内流体的流动特性[J].化工学报，2010，61(5)：1089～1096.

[9] 马源，曹文瑾，林梅.矩形截面螺旋通道内的二次流流场特性[J].西安交通大学学报，2014，48(8)：122～127.

[10] Bolinder C J.Flow Visualization and LDV Measurements of Laminar Flow in a Helical Square Ducts with Finite Pitch[J].Experimental Thermal and Fluid Science，1995，11(4)：348～363.

[11] 张鸣远，陈学俊.螺旋管内气-水两相流流型转换的研究[J].核科学与工程，1983，3(4)：298～304.

[12] Yih- yun Hsu，Graham R W.Transport Processes in Boiling and Two- phase Systems[M].Washington D C：Hemisphere Publishing Company，1986.

[13] 赤川浩尔.气液两相流动[M].杭州：浙江大学出版社，1976.

[14] Tribbe C，Muller- Steinhagen.Structure of Two- phase Flow in Coiled Tubes[J].Multiphase Flow，2007，(26)：10～19.