一种多参数模糊神经网络控制系统调度算法
2015-01-13时维国张明华
时维国 张明华 邵 诚
(1.大连交通大学电气信息学院,辽宁 大连 116028;2.大连理工大学控制科学与工程学院,辽宁 大连 116024)
网络控制系统是一种基于网络的实时反馈控制系统,网络作为物理传输介质被所有设备共享,控制器不能在任意时刻发送与接收数据,必须竞争得到网络的访问权才能发送数据,所以有必要对网络中控制系统的数据传输进行调度管理,合理分配网络资源,使网络中的数据传输具有可管理性和可预测性,尽量降低网络诱导时延对控制系统造成的影响,保证控制性能和系统稳定性。
基于优先级的经典网络调度算法通常采用任务的一个特征参数来确定优先级。Walsh G C和Ye H提出TOD(Try-Once-Discard)/MET(Maximum-Error-First)算法[1,2],使得最大权误差的节点优先传输数据,其他竞争失败节点丢弃未传输数据。Yepez J 等提出LEF(Large Error First)动态调度算法[3],以被控对象的实际响应与期望相应的差值确定优先级。程禹等提出的EDF(Earliest Deadline First)算法只利用消息的截止期作为优先级的依据[4],然而某些数据的重要度确定与控制系统性能有关,与数据的截止期错过率无关。因此,优先级仅由某个特征参数确定是不够的。Mittal A等综合考虑消息的截止期与重要度共同决定消息的优先级[5],假定周期性数据比非周期数据的优先级高,为了保证重要非周期数据能够在截止期内完成传输,引入非周期数据的重要度,其主要与紧急程度和该数据与控制的关系决定。尽管正常情况下该算法表明了其最优性,但在过载情况下,系统会出现急剧的性能降级。周本海等利用综合任务的多种参数来考虑任务优先级[6],降低了任务的截止期错过率,改善了实时调度性能。*收稿日期:2015-04-29(修改稿)基金项目:国家高技术研究发展计划(“863”计划)项目(2014AA041802-2);辽宁省教育厅计划项目(L2012160)
神经网络是从仿生学角度模拟人脑神经系统的运作方式,它具有自组织、自适应和自学习的功能[7,8]。近年来,由模糊控制和神经网络两者交叉综合产生的模糊神经网络成为研究的热点,在复杂工业对象的建模和控制领域得到了广泛应用。秦炎峰和陈铁军将模糊推理系统中的模糊逻辑规则和隶属度函数通过神经网络自学习来整定[9],解决了模糊控制系统中模糊规则缺乏自学习能力及控制精度较低等问题。傅惠等设计了基于Sugeno型神经模糊系统的交通流状态预测算法[10],利用神经网络优化调整模糊推理系统的隶属度函数和模糊规则,并验证了此预测系统相比常规模糊系统具有更好的状态预测性能。李佳宁等设计的控制系统由神经模糊预测器和神经模糊控制器组成[11],提出了一种基于强化学习的神经模糊控制系统和相应的学习算法,实现了基于非训练数据的神经模糊控制器在线学习。以上算法多应用于控制器设计、预测控制、模型建立及参数优化等方面,而应用于网络控制系统优化调度方面还不是很完善。
笔者提出了一种多变量的模糊神经网络调度策略,以神经网络的自学习能力对模糊控制规则进行训练、记忆,确定网络需求度。采用动态权重调整算法对网络需求度和描述网络紧急度的空闲时间双参数进行处理,从而对网络控制系统进行优化调度,合理分配了有限网络资源,保证了系统控制性能和稳定性。
1 系统结构
笔者的研究对象是含调度器的多回路网络控制系统,其结构如图1所示。调度器用来确定各控制回路传递数据的优先级。笔者选用由系统误差和误差变化率求得的网络需求度参数同传输空闲时间确定的网络紧急度参数共同确定各回路优先级。采用动态权重算法对确定优先级的参数权重进行优化,综合考虑各参数对回路优先级的影响,确保网络需求度参数较大且空闲参数较小的回路优先级较高,随着参数变化在线调整各回路优先级。
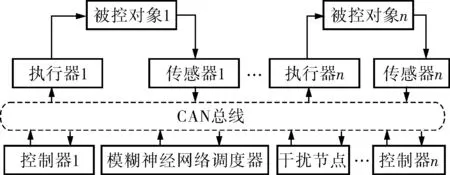
图1 多回路网络控制系统结构框图
笔者从综合网络需求度和网络紧急程度两个方面进行调度优先级的确定。首先,运用神经网络的自学习能力进行训练、记忆模糊规则,确定网络需求度参数vi。然后,以网络需求度参数vi和表征网络紧急度的空闲时间γi作为输入变量,控制回路的优先级Pi作为输出变量。设定任务参数为:n个控制回路实时任务集描述为Γ(τ1,τ2,…,τn);Ti定义为各回路的任务周期;Ci定义为最大计算时间,即在无干扰情况下执行一个任务作业所需的最长执行时间;Di定义为绝对截止时间,任务作业必须在截止期前完成才能得到正确执行结果;γi定义为任务τi的空闲时间,即任务在截止期Di前完成需要等待的时间,设任务的周期Ti=Di,则γi=Ti-Ci;γmax为实际最大空闲时间;γmin为实际最小空闲时间;Ri为网络紧急度;vi表示网络需求度,vi越大任务越重要;Pi为任务优先级,即任务被调度的优先指标,取决于采用的调度策略(假设优先级数越大,优先级等级越高)。
2 网络调度算法的实现
结合各控制回路的网络需求度和网络紧急度,采用动态权重算法确定各回路的优先级。图2所示为模糊神经网络调度参数处理过程。

图2 模糊神经网络调度参数处理过程
2.1 网络需求度处理
对于网络需求度的处理,笔者运用神经网络的学习功能、联想记忆功能和分布并行式处理功能实现模糊控制规则的表示和知识获取。
假设ei和eci的变化范围均为[-1.0,1.0],Ei、Eci为ei、eci的模糊集,Ei的量化等级为11级[-5,-4,-3,-2,-1,0,1,2,3,4,5],Eci的量化等级为9级[-4,-3,-2,-1,0,1,2,3,4];输出Vi的量化等级为5级[1,2,3,4,5]。Ei的模糊子集为{NB、NM、NS、ZE、PS、PM、PB},Eci的模糊子集为{NB、NS、ZE、PS、PB},Vi的模糊子集为{PS、S、M、B、PB}。取量化因子ke=5,kec=4,比例因子Kv=0.2。
选取三角形和梯形隶属度函数混合作为输入变量Ei的隶属度函数,三角形隶属度函数作为输入变量Eci的隶属度函数,梯形隶属度函数作为输出变量Vi的隶属度函数,其函数曲线分别如图3~5所示。以控制回路误差和误差变化率作为模糊神经网络模块的输入,以网络需求度作为输出。当误差和误差变化率较大时,需要分配较多的网络资源;反之,若误差和误差变化率较小时,则分配较少的网络资源。优先级数越大,则其相应的控制回路网络需求度越高。依据专家经验确定的模糊规则作为神经网络初始训练样本进行网络训练,最终实现基于模糊神经网络推理的网络需求度的求解。
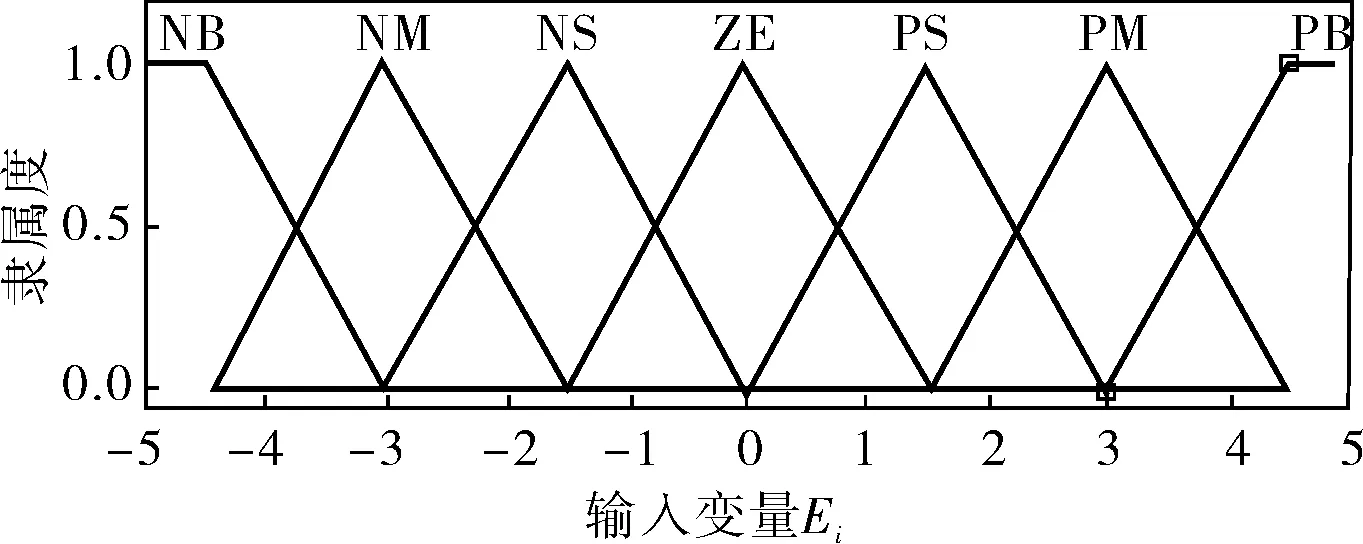
图3 输入变量Ei的隶属度函数
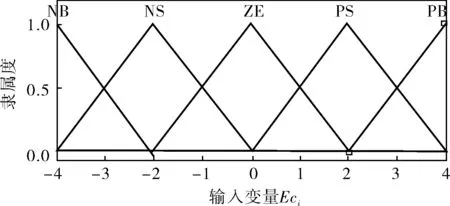
图4 输入变量Eci的隶属度函数

图5 输出变量Vi的隶属度函数
在利用模糊控制决策表的输入、输出参数样本对神经网络进行训练之前,要将训练样本进行归一化处理,即将所有数据按比例放缩到不大于1的范围内。经归一化后得到控制决策表(表1)。利用99组数据可构成训练向量组,神经网络对应输入向量[Ei,Eci],输出空间对应网络需求度向量[Vi],表中的任意一行和一列数据都可以构成一个训练向量组。

表1 归一化的模糊控制决策
神经网络采用隐含层为5个神经元的双输入、单输出的BP网络。模糊神经网络规则的训练与存储需要编写程序实现,利用函数train进行网络训练,拟合采样周期为50个权值调节周期;网络最大学习次数为20 000次;网络误差限为0.01;学习率为0.9。
经过网络训练、曲线拟合完成模糊控制规则的映射,将模糊规则存储到神经网络中,并打包成神经网络模块,用于网络需求度的求取。图6所示为模糊规则推理曲面,图7所示为运用训练形成的神经网络模块求解网络需求度的仿真模块。

图6 推理规则曲面
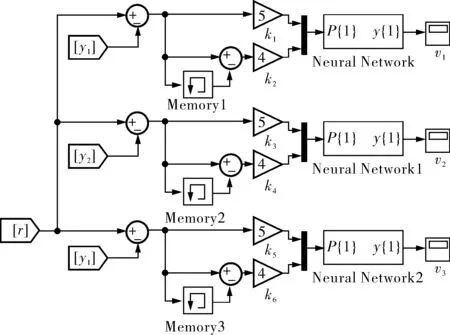
图7 网络需求度仿真模块
2.2 网络紧急度参数处理
经典调度算法通常以任务的一个特征参数来确定任务的优先级。例如,EDF策略将最高优先级指派给截止期最早的任务,LSF(Least Slack First)策略将最高优先级指派给空闲时间最短的任务[12]。尽管在正常的系统负载下这些算法均具有最优性,但在超载情况下,系统性能严重降低,使得关键任务失去可调度性。考虑任务重要特性的双参数调度算法可以克服单参数调度的缺陷,通过优先执行具有最大价值或最关键的任务尽可能避免系统失效甚至崩溃情况的出现[13]。
采用任务的空闲时间γi作为网络紧急程度的表征参数。由于空闲时间是一个不确定的参数,在此设定相对截止时间等同于任务的周期,即γi=Ti-Ci,各回路的网络紧急程度为:

(1)
2.3 参数权重确定
综合考虑任务的控制性能和任务作业空闲时间进行优先级动态调整过程。笔者运用动态权重算法来确定各控制回路的动态优先级。将权重ωi(k)分为固定权重ω0i(k)和补偿权重Δωi(k),则任意回路权重值为:
ωi(k)=ω0i(k)+Δωi(k)
ω0i(k)={ω01(k),ω02(k),…,ω0n(k)},ω0i(k)∈(0,maxω)
(2)
Δωi(k)={Δω1(k),Δω2(k),…,Δwn(k)},
Δωi(k)∈[Δωmin,maxω-ω0i(k)]
其中,maxω为系统中最大权重系数,Δωmin为最小的补偿权重系数。动态补偿权重Δωi(k+1)可依据被控对象状态,通过映射函数[14]得到:
(3)
约束条件为maxω-ω0i(k),|ei(k)|≥|ei(k)|s,0<|ei(k)|<|ei(k)|s。δ为动态权重修正因子,|ei(k)|s为补偿权重饱和时的误差。将映射函数代入式(1)中,可求取权重ωi(k+1)。在对优先级进行配置过程中要对资源按照权重进行比例分配,将权重ωi(k+1)进行标称值转换:
(4)
记任务为τi(Ti,Ci,Vi),设定在不同负载下进行网络调度,负载高即干扰节点传输所占的网络带宽较高。笔者设计的网络优先级调度最终要达到以下目的:当负载较大时,控制回路优先级主要取决于网络需求度,其次考虑任务传输的紧急程度。以网络需求度高的优先传输为前提,比较任务的紧急程度。运用动态权重算法得到优先级判定公式:
(5)
综上,多参数模糊神经网络调度算法如下:
a. 确定模糊推理的输入参数为误差和误差变化率,输出参数为网络需求度,并依据专家经验确立模糊规则。
b. 利用归一化程序对模糊规则归一化处理,采用BP神经网络,编写程序,实现模糊神经规则的训练与存储,运用网络需求度仿真模块求解网络需求度参数vi。
c. 确定网络紧急程度Ri。将空闲时间γi和约束条件代入式(1)计算网络紧急程度Ri。

e. 比较各回路的优先级,确定各回路调度顺序,优先级大,则先调度。
3 仿真实验
对控制系统做如下说明:传感器为时间驱动,控制器和执行器为事件驱动;将传感器的优先级作为控制回路的优先级,调度器中的队列只保存最新的采样值;基于模糊的优先级配置策略需在基于优先权的网络上实现,笔者选择CAN总线。
仿真研究含有3个回路的网络控制系统模型。被控对象为直流电机,传递函数均为:

采用离散PID控制器,参数取值为:比例系数K=1.5,微分系数Td=0.035,积分系数Ti=0.12,微分增益N=10000。利用TrueTime仿真计算,参数设置为:CAN总线,数据包传输速率80kbit/s。固定权重最大值maxω=1,设定ω01(k)=0.25,ω02(k)=0.25,ω03(k)=0.25,Δωmin=0.01,补偿权重饱和误差|ei(k)|s=0.25,修正因子δ=1.25。3个回路的采样周期分别为T1=10ms,T2=10ms,T3=10ms,任务作业执行时间Ci为4ms,调度调整周期T为10ms,输入为单位阶跃信号,分别采用模糊神经网络的调度算法和EDF调度算法进行仿真。
3.1 输出响应曲线
图8所示为基于模糊神经网络调度算法仿真的时序图,分别对应3个回路控制器节点的时序。由图8可知,模糊神经网络调度器能够合理安排各回路数据在网络传输中的先后顺序,避免网络堵塞。对比图9、10可知,在带宽受限的情况下,由于EDF调度算法是根据截止期对优先级进行动态调整的,因此回路3输出响应曲线相对回路1和回路2的稳定性能较差,且响应曲线具有较大超调量,图中方波为参考输入。而对应以模糊神经网络调度算法得到响应曲线中回路3相比EDF算法有很大提高,这主要是动态优先级调整的作用,根据各个控制回路实时运行时特征参数有目的地调整和优化不同重要度的控制回路的传输优先级,合理地分配优先级,使各回路均有好的响应。
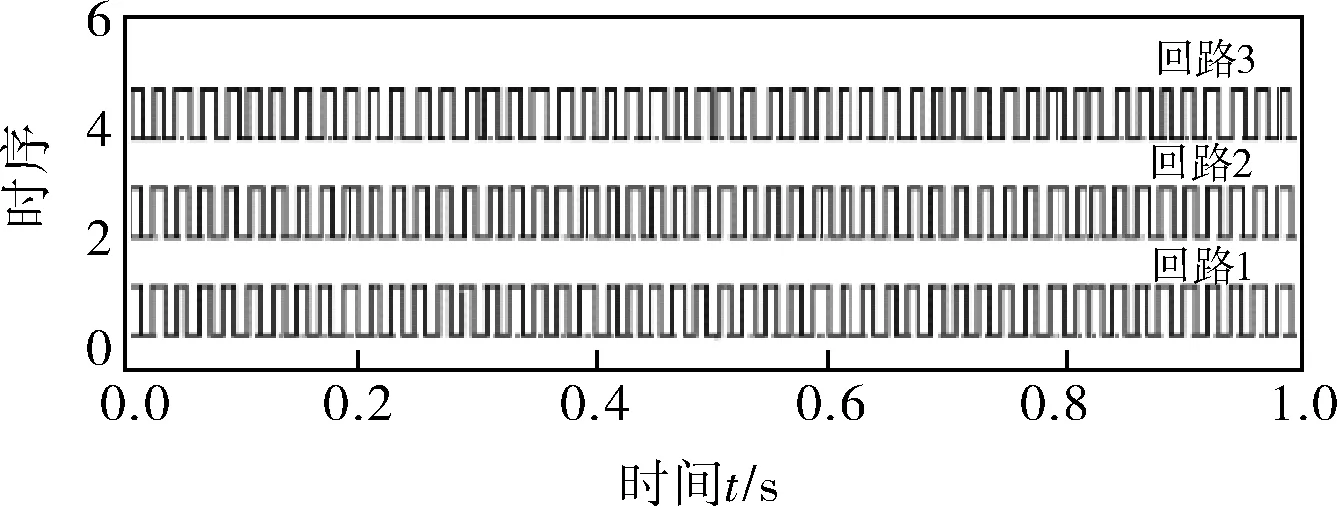
图8 基于模糊神经网络调度算法的时序

图9 基于EDF调度的控制效果

图10 基于模糊神经网络调度的控制效果
3.2 控制性能IAE
分别针对基于EDF和模糊神经网络调度算法中的回路3,选择性能指标IAE进行仿真,得到的IAE值如图11所示。通过对比,进一步表明了模糊神经网络调度具有更好的控制效果。

图11 控制回路3的IAE值
4 结束语
在模糊反馈调度算法的基础上提出了一种模糊神经网络调度算法。将模糊控制和神经网络结合起来,利用神经网络的并行处理能力使模糊系统的推理能力得到提高。采用动态权重调节策略,同时考虑系统的输出误差、误差变化率和空闲时间,设计了模糊神经网络调度器,对各回路优先级进行动态调整,同时提高了系统的控制性能。仿真结果表明,相同情况下模糊神经网络调度算法比EDF算法产生更小的IAE,具有更好的控制性能,不会出现某个回路优先级过低不被调度的情况。笔者的下一步工作是将模糊神经网络调度策略在不同负载下的性能进行优化,与变采样周期算法相结合,实现调度与控制的协同设计,进一步提高系统的性能。
[1] Walsh G C,Ye H,Bushnell L G.Stability Analysis of Networked Control Systems[J].IEEE Transaction on Control Systems Technology,2002,10(3):438~446.
[2] Walsh G C,Ye H. Scheduling of Networked Control Systems[J].Control Systems,IEEE,2001,21(1): 57~65.
[3] Yepez J,Marti P,Fuertes J M.Control Loop Scheduling Paradigm in Distributed Control Systems[C].The 29th Annual Conference of the Industrial Electronics Society.Roanoke:IEEE,2003:1441~1446.
[4] 程禹,赵宏伟,龙曼丽,等.最早截止期优先调度算法的改进[J].吉林大学学报(工学版),2013,43(5):1338~1342.
[5] Mittal A, Manimaran G, Murthy C S R. Dynamic Real-time Channel Establishment in Multiple Access Bus Networks[J].Computer Communications,2003,26(2):113~127.
[6] 周本海,王溪波,乔建忠,等.基于多参数的μC/OS-II任务优先级和调度方法[J].计算机工程,2007,33(21):28~30.
[7] 石纯芳.基于神经网络的高温压力管道涡流检测信号的温度补偿研究[J].化工机械,2012,39(2):174~176.
[8] 陈雅群,郭雷,张树生,等.基于两种神经网络的管内沸腾汽液两相流型识别[J].化工机械,2010,37(6):763~766.
[9] 秦炎峰,陈铁军.自适应神经模糊推理系统的参数优化方法[J].微计算机信息,2008,24(18):222~224.
[10] 傅惠,许伦辉,胡刚,等.基于Sugeno型神经模糊系统的交通流状态预测算法[J].控制理论与应用,2010,27(12):1637~1640.
[11] 李佳宁,易建强,赵冬斌,等.一种基于强化学习的在线神经模糊控制系统[J].中国科学院研究生学报,2005,22(5):631~638.
[12] 张杰.最早截止期优先实时调度算法研究[D].武汉:华中科技大学,2009.
[13] 沈青,桂卫华,熊英,等.双参数模糊调度在实时控制系统中的应用[J].中南大学学报(自然科学版),2009,40(2):441~446.
[14] 田中大,高宪文,史美华,等.资源受限网络控制系统的模糊反馈调度[J].电机与控制学报,2013,17(1):94~101.
