双Y 移30° PMSM 双电机串联系统的建模与仿真

张少一，刘华菘，史贤俊，刘陵顺

(海军航空工程学院，烟台264001)

0 引 言

在常规的多相电机驱动系统中，每一台电机都由一台逆变器电源供电，因此在需要多台电机驱动的场合，整个驱动系统的设备数量多，占用空间大。本文研究了一种新颖的多电机串联驱动系统，它将两台双Y 移30°PMSM 的定子绕组按照一定的规则串联在一起，由一台逆变器电源供电，实现对每一台电机运行的解耦控制，有助于节省一套驱动和控制系统［1］。目前国内外对于该串联系统的研究大多集中在多相感应电机串联驱动系统［2－4］，对于永磁同步电机串联系统的研究还较少见［5－7］。本文以基于单逆变器驱动的双Y 移30°PMSM 双电机串联系统为研究对象，为了实现该串联系统的控制建模需求，分别建立了串联系统在自然坐标系下、静止两相坐标系下以及同步旋转坐标系下的数学模型，研究了基于id=0 的电流滞环PWM 技术下的矢量控制策略，并给出了变负载系统运行仿真分析，实现了两台电机在同一台逆变器下的独立解耦运行。

1 串联驱动系统的数学建模

两台定子绕组正弦分布的双Y 移30°六相电机串联系统原理图如图1 所示。

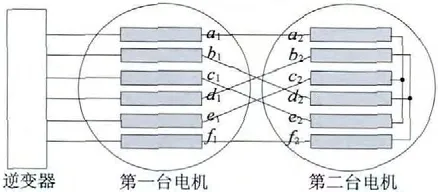
图1 两台双Y 移30°六相电机组成的串联驱动系统

1.1 自然坐标系下的数学模型

面装式PMSM 定子永磁体产生的励磁磁场在气隙中正弦分布，设Ns1，φsm1，θr1为第一台电机定子绕组的匝数、永磁体磁路主磁通、转子磁场与定子A相绕组的夹角;Ns2，φsm2，θr2为第二台电机定子绕组的匝数、永磁体磁路主磁通、转子磁场与定子A 相绕组的夹角。θ =30°，则两台电机的转子磁场在定子绕组中产生的磁链:

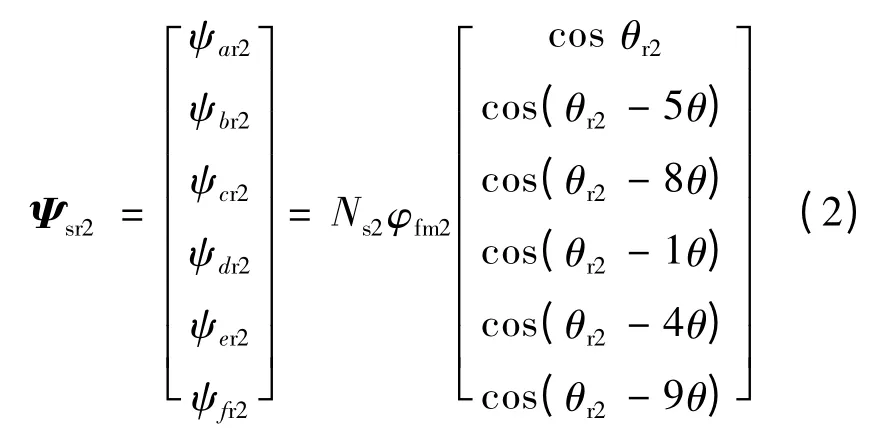
由于两台电机对应的相绕组串联在一起，它们的定子相电流对应相等，等于逆变器输出电流，设串联系统输入端的输入电流为Is=［iAiBiCiDiEiF］T，则两台电机定子绕组的总磁链分别:

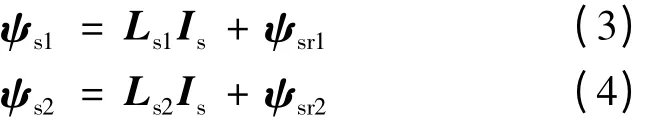
设rs1为第一台电机定子相绕组电阻，rs2为第二台电机定子相绕组电阻，则它们的定子电压方程可以描述为:

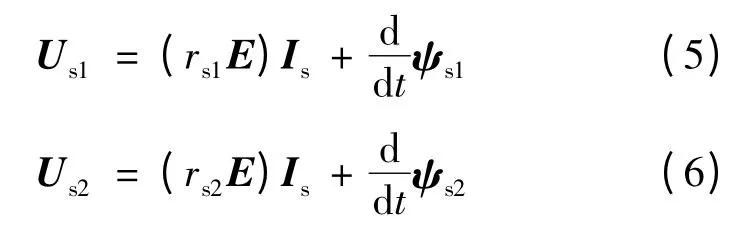
又由于两台电机定子绕组串联在一起，所以逆变器的输出电压:

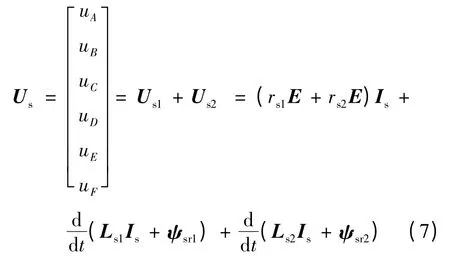
设p1，p2分别为两台电机的极对数，两台电机的磁场能量分别:

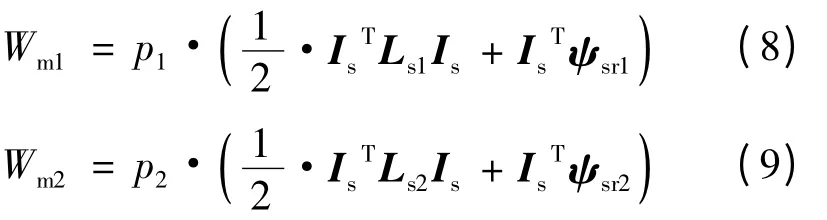
则转矩公式:

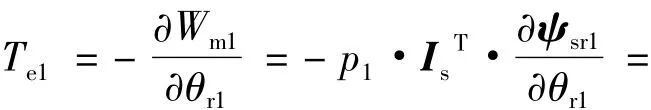
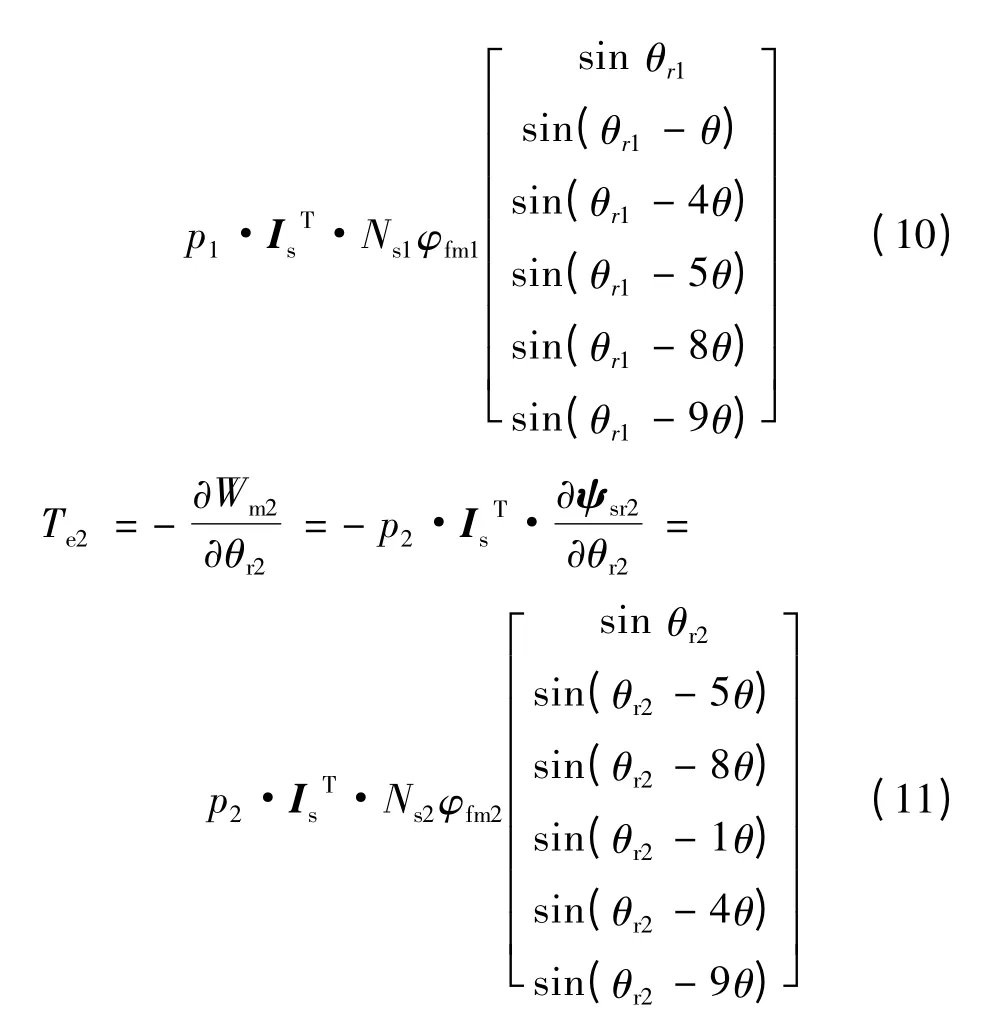
设J1，F1，Tl1，ωr1分别为PMSM1 的转动惯量、摩擦系数、负载、转速;J2，F2，Tl2，ωr2分别为PMSM2 的转动惯量、摩擦系数、负载、转速，则两台串联PMSM 的运动方程为:

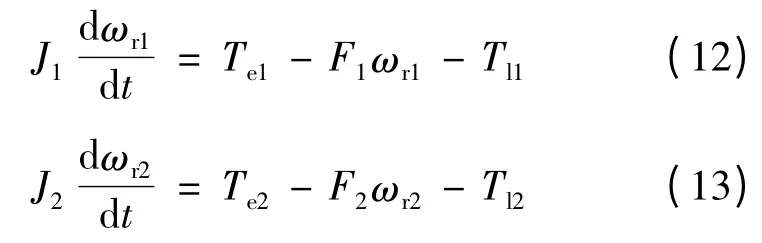
1.2 两相静止坐标系下的模型

运用空间矢量变换矩阵T 对静止坐标系下的数学模型进行变换，将自然坐标系下的数学模型变换到三个相互正交的平面的思路，将逆变器输出电压分解成三个部分。

在α－β 平面内有:

在x－y 平面内有:

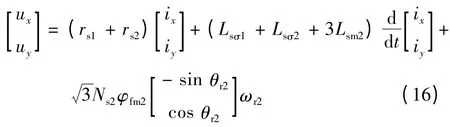
在O1－O2平面内有:

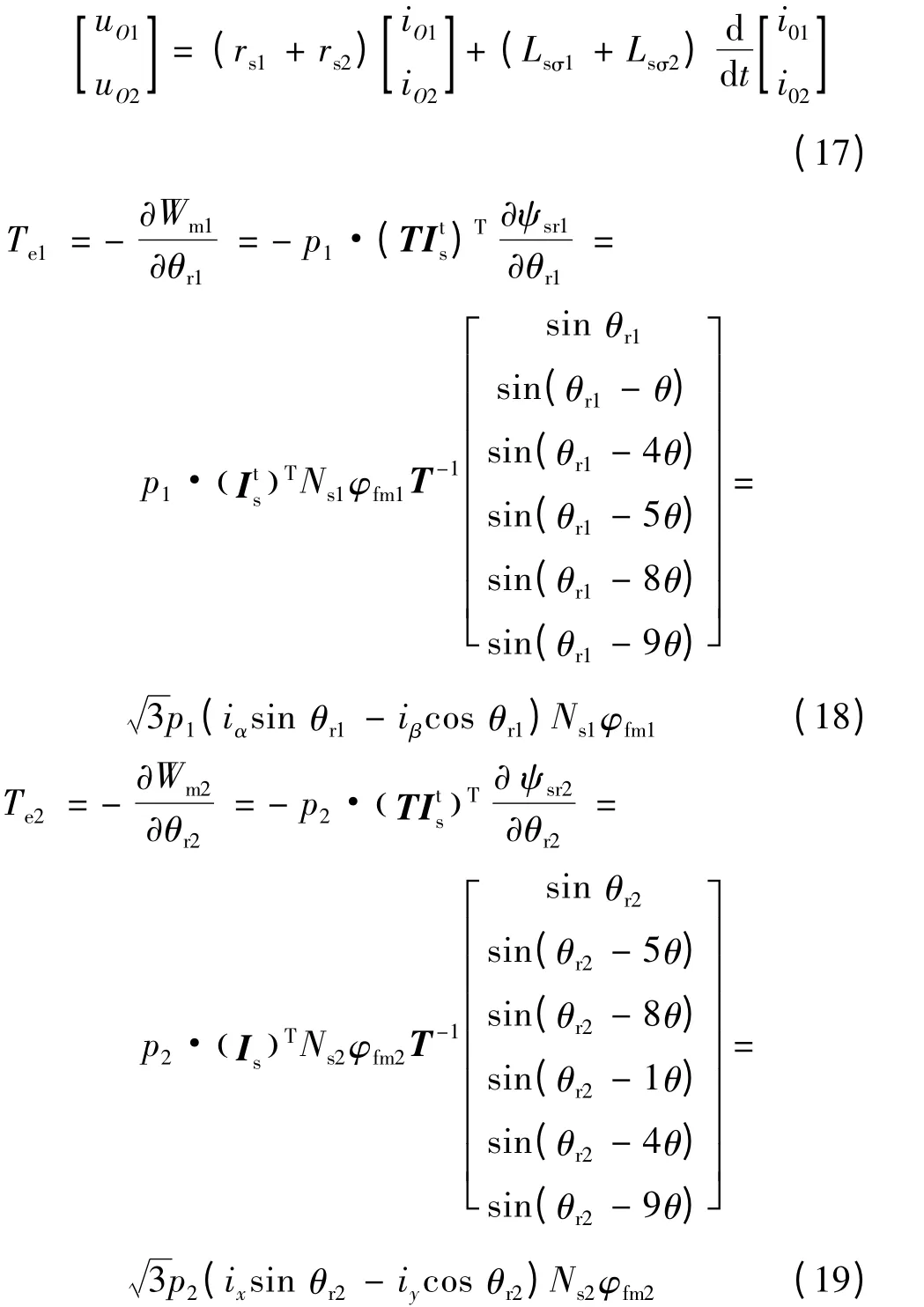
因此，第一台电机的转矩只由α－β 平面内的电流分量iα和iβ控制;第二台电机的转矩只由x－y平面内的电流分量ix和iy控制。空间矢量变换可以将自然坐标系下六相电机的控制在静止两相坐标系中实现，变换后的电压方程和电机转矩方程是两台电机串联驱动系统实现解耦控制的数学根据。

1.3 两相旋转坐标系下的模型

将两相静止坐标系下的数学模型通过同步旋转变换矩阵转换到旋转坐标系下［5－7］，旋转坐标变换可以消除参数θr1，θr2，得到系统在d－q 旋转坐标系下的简化模型。

令ψf1=Ns1φfm1，R =rs1+rs2，L1=Lsσ1+Lsσ2+3Lsm1，则在d1－q1坐标系中有电压关系式:

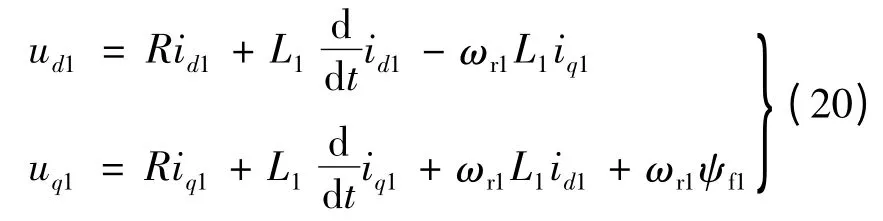
同理，令ψf2=Ns2φfm2，L2=Lsσ1+Lsσ2+3Lsm2，则在d2－q2坐标系下有电压关系式:

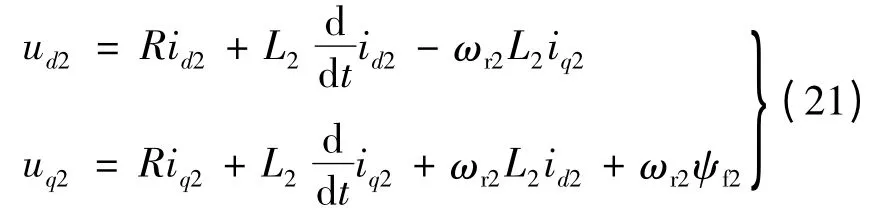
将iα=id1cos θr1－iq1sin θr1，iβ=id1sin θr1+iq1cos θr1代入第一台电机的转矩方程式(18)中有:

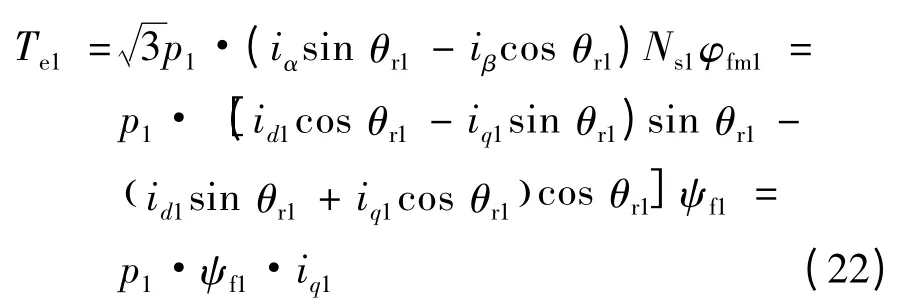
将ix=id2cos θr2－iq2sin θr2，iy=id2sin θr2+iq2cos θr2代入第二台电机的转矩方程式(19)中有:

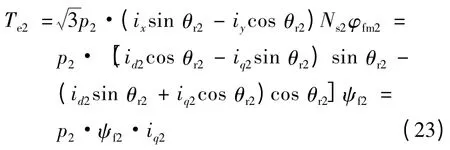
两台电机的电磁转矩的大小只需要通过控制iq1和iq2来实现。iq1和iq2这两个电流分量是可以独立调节的，因此在串联驱动系统中可以实现电机的独立控制。

2 变速仿真研究

串联系统采用基于电流滞环PWM 控制技术的id=0 矢量控制策略，原理图如图2 所示。

设定两台电机的负载为零，通过设定转速指令来改变相应电机的转速，获得了两台电机的转速响应波形、逆变器A 相电流波形和两台电机的转矩响应波形如图3、图4 所示。

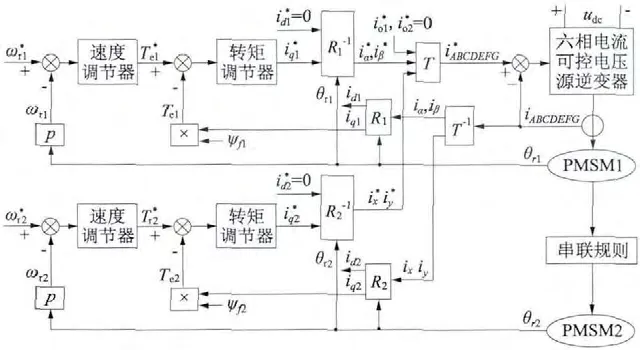
图2 两台六相PMSM 串联矢量控制系统

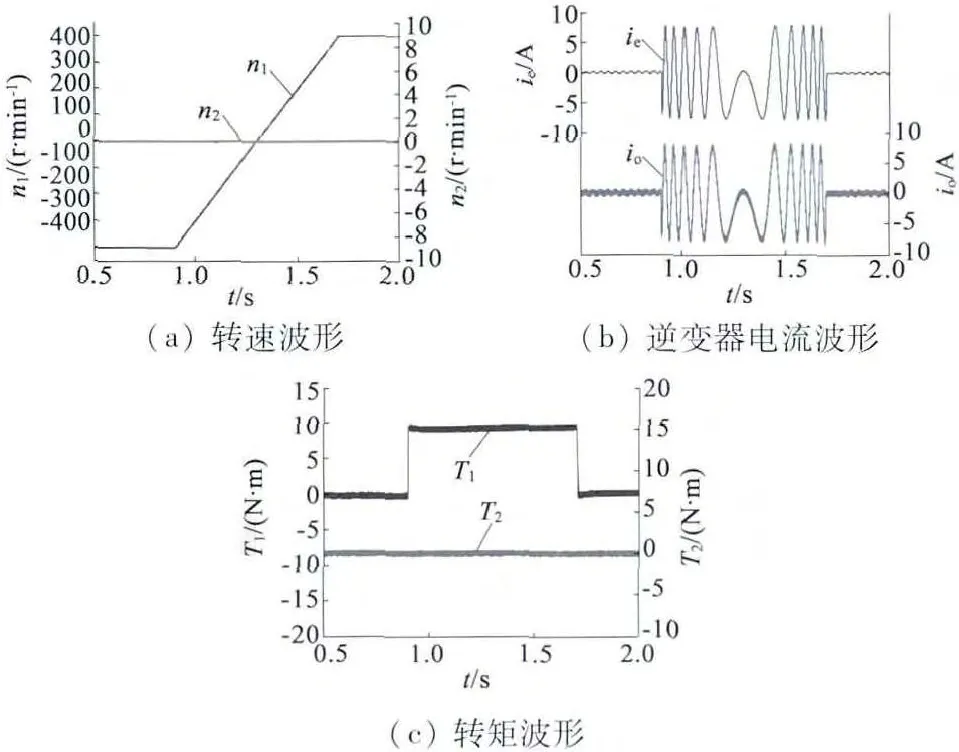
图3 电机2 保持静止，电机1 从－400 r/min 变速到400 r/min 过程的仿真波形

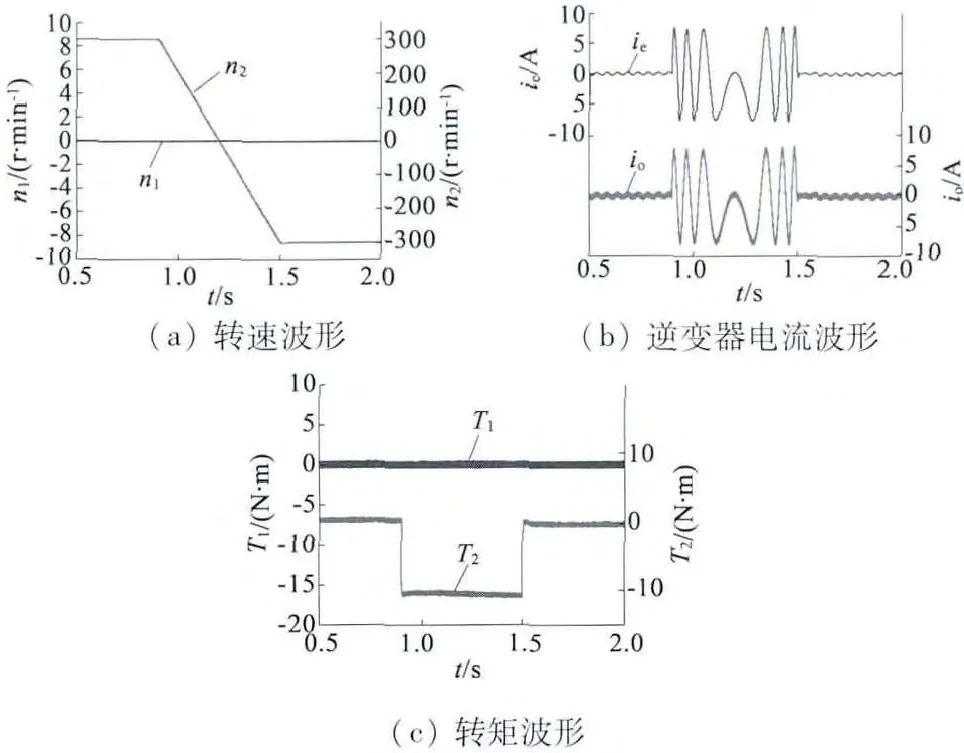
图4 电机1 保持静止，电机2 从300 r/min 变速到－300 r/min 过程的仿真波形

结果表明:串联系统中任意一台PMSM 的运行工况的改变均不会对与其串联的另一台PMSM 构成干扰，串联电机可以实现在同一台逆变器供电下解耦运行。

3 结 语

本文研究了单逆变器驱动的双Y 移30°PMSM双电机串联系统数学建模问题，分别建立了不同坐标系下的数学模型。为了验证所建数学模型的正确性，建立了基于id=0 的电流滞环PWM 技术下的矢量控制策略，并给出了变负载系统运行仿真分析，实现了两台电机在同一台逆变器下的独立解耦运行。

［1］ LEVI E，JONES M.A novel concept of a multiphase multi－motor vector controlled drive system supplied from a single voltage source inverter［J］. IEEE Transactions on Power electronics，2004，19(2):320－335.

［2］ LEVI E.Multiphase electric machines for variable－speed applications［J］. IEEE Transactions on Industrial electronics，2008，55(5):1893－1909.

［3］ LEVI E，JONES M. Modeling control and experimental investigation of a five－phase series－connected two－motor drive with single inverter supply ［J］. IEEE Transactions Industry Electrical，2007，54(3):1504－1516.

［4］ 刘陵顺，张海洋，苗正戈. SVPWM 控制两台双Y 移30°PMSM串联系统研究［J］.电气传动，2012，42(8):39－42.

［5］ 史贤俊，刘陵顺，周绍磊. 基于SVPWM 的六相PMSM 串联系统运行性能研究［J］.微电机，2013，46(1):28－32.

［6］ 江丽雅，张少一. 双Y 移30°永磁同步电动机串联系统的仿真［J］.海军航空工程学院学报，2013，28(5):475－479.

［7］ 苗正戈，刘陵顺，张海洋.两个不同结构六相永磁同步电机串联驱动系统［J］.电机与控制应用，2011，38(7):17－21.