基于粒子群算法的喷水减温器建模研究

金秀章 曹丁元 谢泽坤 孙小林

(华北电力大学控制与计算机工程学院，河北 保定 071003)

喷水减温是将水直接喷入过热蒸汽中，水被加热、汽化和过热，吸收蒸汽的热量，从而达到调节主蒸汽温度的目的[1]。喷水减温器的工作状况直接影响到主蒸汽的品质，因此对喷水减温器进行建模，对其动态性能的了解具有重要的现实意义。目前，国内外对喷水减温器的机理建模研究已经很普遍[2～5]，但是与智能建模结合起来进行的模型参数优化并不多，笔者主要研究基于粒子群优化算法(PSO)的喷水减温器机理建模。

PSO是由Kennedy J和Eberhart R于1995年提出的一种仿生优化计算方法[6]，采用了基于种群的全局搜索策略和简单的速度-位移模式[7]，具有便于实现、计算速度快的优点。近几年，专家学者对PSO进行了大量研究，将PSO应用在了不同的领域[8～10]，为PSO的应用与发展做出了巨大的贡献。

1 喷水减温器数学模型分析①

某热电厂机组喷水减温器的简图如图1所示，图中G1、h1、T1分别表示喷水减温器入口处主蒸汽的质量流量、焓值和温度；G、h、T分别表示喷水减温器出口处主蒸汽的质量流量、焓值和温度；Gw、hw、Tw分别表示喷水减温器入口减温水的质量流量、焓值和温度；Qm为流体从壁面吸收的热量。

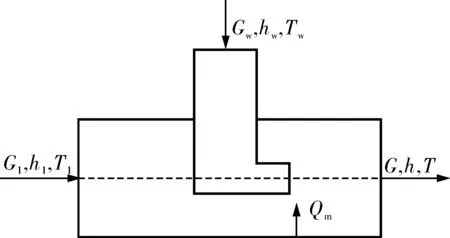
图1 喷水减温器简图

在燃烧工况不变的情况下，即Δh1=0，根据喷水减温器的生产工艺、能量守恒定律和质量守恒定律可以得到减温水流量对主蒸汽温度影响的数学模型。由于整个喷水减温器内的流体具有分布参数特点，其状态参数不仅是时间还是空间上的函数。这种分布参数特点使得到的数学模型都是非线性偏微分方程组，这些偏微分方程组含有长度和时间两个自变量。这样一个分布参数系统的非线性模型是十分复杂的，计算也有一定难度。为了简化问题，在建立数学模型时，将流体状态参数看成一致的，并在空间位置上选定一个有代表性的点，例如出口点，利用这一点介质的参数作为环节的集总参数。

为了便于分析，对喷水减温器的换热通道作几个合理的假设：

a. 流道内汽水两相介质流体混合均匀，且流速相同；

b. 流体只做轴向运动，且同一横截面的流体参数相同；

c. 所有减温器横截面均近似相等；

d. 对于减温器金属壁面，忽略轴向传热，仅沿径向传热；

e. 忽略流体在流动过程中受到的阻力；

f. 整个系统与外界环境之间绝热。

在上述简化假设条件下，以喷水减温器出口点参数作为集总参数列出如下平衡方程：

减温器内流体质量守恒方程

(1)

减温器内流体热平衡方程

(2)

减温器金属壁面对流体传热方程

Qm=αA(Tm-T)

(3)

减温器金属壁面热平衡方程

(4)

Q1=G1(h1-h)

(5)

Qw=Gw(h-hw)

(6)

式中Q1——单位时间内减温器内蒸汽的放热量；

Qw——单位时间内减温水的吸热量。

对式(1)～(6)进行线性化和偏差化处理，再进行拉氏变换可得到喷水量变化对主蒸汽温度变化的传递函数：

(7)

式中cp——出口主蒸汽的定压比热容；

Tm——减温器金属壁面蓄热时间常数；

αD——动态参数；

τ0——蒸汽通过整个喷水减温器的平均时间。

由式(7)可以看出传递函数的增益K=(hw-h1)/[(G1+Gw)cp]，时间常数T=0.5(τ0+TmαD)，阶次n=2。由于该传递函数是在合理假设的情况下作出的，K、T、n并不精确，因此这3个参数都需要进一步进行辨识，笔者利用粒子群优化算法进行参数辨识。

2 粒子群优化算法

粒子群优化算法的基本思想是把每个优化问题的解都看成是搜索空间中的粒子[7]，所有的粒子都有一个被优化的函数决定的适应值，每个粒子还有一个速度向量决定它们飞翔的方向和距离，然后粒子就追随当前的最优粒子在解空间中进行搜索。首先初始化一群随机粒子，然后通过迭代搜索最优解。在每一次迭代中，粒子通过跟踪两个最优值来更新自己，第一个就是粒子本身目前所找到的最优解Xbesti，即个体最优值；另一个最优值是整个种群目前找到的最优解Xbestg，即全局最优解。

下面以求某一函数Q(X)的极小值为例，介绍基本粒子群算法的实现方法。

假设在一个N维目标搜索空间中，有m个粒子组成的一个群体，其中第i个粒子的位置表示为向量Xi=(xi1,xi2,…,xiN),i=1,2,…,m；其速度也是一个N维向量，记为Vi=(vi1,vi2,…,viN)。随机产生一组Xi作为第一代初始种群，将Xi代入目标函数Q(Xi)就可以计算出其适应值，根据适应值的大小衡量Xi的优劣。对于最小化问题，目标函数值越小，对应的适应值越好，记为Qbesti。粒子i的当前最好位置可表示为：

(8)

粒子Xi根据下式更新速度和位置：

Vin(t+1)=ωvin(t)+c1r1[Xbestin-xin(t)]+

c2r2[Xbestgn-xin(t)]

(9)

xin(t+1)=xin(t)+vin(t+1)

(10)

式中c1、c2——正实数，称作加速因子，用来调节每次迭代的步长；

r1、r2——[0,1]范围内变化的随机函数；

ω——惯性权重，用于全局搜索和局部搜索。

3 基于粒子群优化算法的智能辨识

粒子群优化算法辨识流程如图2所示。系统辨识的过程实质上就是函数拟合的过程，这里包括传递函数的结构和参数。上文已经通过机理建模得到喷水减温器的机理模型，但是由于机理模型是建立在系统简化和一些理想假设的前提下，模型并不很准确，但是得到了模型的基本结构。此时，通过粒子群优化算法来优化模型的参数，最终得到精确的传递函数。

图2 粒子群优化算法辨识流程

4 优化结果分析

现场采集到的数据并不能直接用于求取系统的传递函数，系统的传递函数是在零初值条件下定义的[11],因此在进行辨识之前，需要对现场数据进行零初值化处理。利用Matlab将现场数据零初值化处理后得到的数据曲线如图3所示。

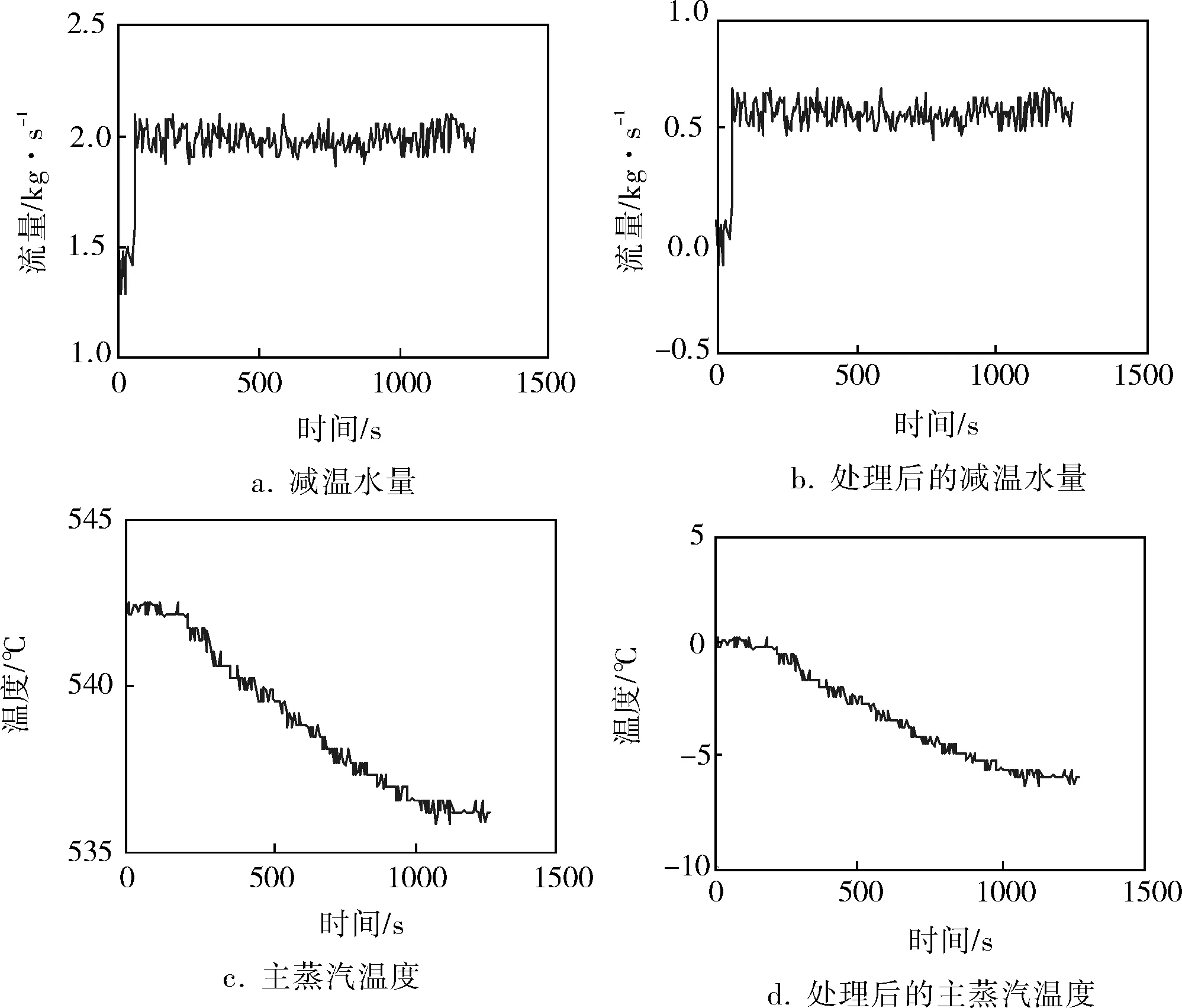
图3 现场数据和零初值化处理后的数据曲线

由式(7)总结出喷水减温器的机理模型为：

(11)

选择论域为K∈(-20,0),T∈(5,500),n∈(2,5)。利用Matlab对零初值化处理后的现场数据进行辨识得到图4所示的结果，并且确定了式(11)中的待辨识参数，得到喷水减温器的传递函数为：

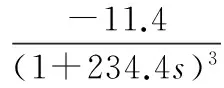
(12)

图4 辨识结果与实测现场数据对比

由图4可以看出辨识结果与实测数据基本吻合，式(12)的传递函数能很好地反映系统的动态特性。

5 结束语

喷水减温器直接影响锅炉主蒸汽品质，笔者根据喷水减温器生产工艺研究了它的机理模型。由于机理模型是在理想情况下建立的，因此并不能精确地反映喷水减温器的动态特性，机理模型的参数有待辨识。针对此不足，笔者采用粒子群优化算法，根据现场采集到的数据，对机理模型的参数进行优化辨识，得到了比较精确的模型。

[1] 容銮恩,袁镇福,刘志敏,等.电站锅炉原理[M].北京:中国电力出版社,1997.

[2] Schoonover K G，Ren W M,Ghiaasiaan S M,et al.Mechanistic Modeling of Desuperheater Performance[J].ISA Transactions,1996,35(1):45～51.

[3] 宁德亮,庞凤阁,高璞珍.喷水减温器动态仿真模型的建立及其解法[J].核动力工程，2005,26(3):280～283.

[4] 闫涛,杨青瑞,尚伟，等.喷水减温器简易建模方法及Simulink仿真研究[J].硅谷,2009,(8):21～23.

[5] 方彦军,王振宇.超超临界机组直流锅炉喷水减温器的建模研究[J].热力发电,2012,41(12):39～42.

[6] Kennedy J, Eberhart R C.Particle Swarm Optimization[C].IEEE International Conference on Neural Net-works.Piscataway：IEEE，1995:1942～1948.

[7] 韩璞,董泽,王东风，等.智能控制理论及应用[M].北京:中国电力出版社,2012.

[8] 朱艳伟,石新春,但扬清，等.粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用[J].中国电机工程学报,2012,32(4):42～48.

[9] 霍延军.基于量子粒子群算法的PID参数自整定方法[J].微电子学与计算机,2012,29(10):194～197.

[10] 严巳杰，胡建华，黄炳琼，等.基于粒子群优化算法的板翅式换热器优化设计[J].化工机械，2012,39(1):55～57.

[11] 胡寿松.自动控制原理[M].北京:科学出版社，2007.