基于MCUSUM-ForeCA的微小故障检测

林圣才 李 楠 杨煜普

(上海交通大学电子信息与电气工程学院系统控制与信息处理教育部重点实验室，上海 200240)

20世纪90年代以来，现代工业过程向着大规模和复杂化的方向发展，导致工业过程越来越难以用精确的物理模型去描述。由此基于多元统计分析的故障检测方法应运而生，并在工业过程中获得了成功的运用[1～3]。但是传统的多元统计方法也存在着自身的缺陷，如对微小故障不灵敏及PCA[4]方法要求数据服从高斯分布等。随着工业过程的长期运行，过程中存在着设备老化等缓慢变化，这些变化轻则导致产品质量下降，重则可能会导致工业过程发生故障进而出现事故，因此此类问题亟待解决。

针对此类微小故障问题，笔者引入多元累积和(Multivariate Cumulative Sum,MCUSUM)控制图[5]和可预测元分析[6](Forecastable Component Analysis,ForeCA)，提出了MCUSUM-ForeCA方法。MCUSUM控制图用于统计多个变量的历史累积信息，而ForeCA是一种全新的用于多变量时序相关信号的降维与特征提取方法，它能从历史数据中捕捉系统的动态特性，并以此来预测系统的运行变化趋势。MCUSUM-ForeCA方法首先使用MCUSUM对数据进行处理，获取累积信息，然后使用ForeCA算法提取过程数据中的可预测分量，构造两种统计量对过程进行统计监控。在TE过程上的仿真结果表明了此方法的可行性和有效性。MCUSUM-ForeCA方法不但克服了传统多元统计方法无法反映过程时序特性的不足，而且在对微小故障的检测上显示了良好的性能。

(1)

其中Sj表示到第j个样本为止的累积和。如果过程均值保持不变，则Sj将会在0周围随机波动；如果过程均值产生了较大的变化(上升或下降)，则Sj会跟随着产生相同方向的变化。

2 可预测元分析

设矩阵X∈Rn×m，假设线性变换WT∈Rk×n，使得S=WTX，其中S为从X中提取的可预测分量。ForeCA算法的目的就是寻找能够满足这个要求的线性变换WT。

(2)

(3)

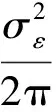
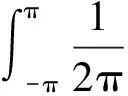
(4)

对式(4)进行变换后，可得平稳过程的可预测度为：

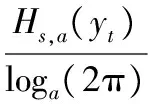
(5)

对于多变量二阶平稳过程Xt，考虑线性变换yt=wTXt，其中w是W的列向量，w∈Rn，此时yt就可以看成是一个单变量的二阶平稳过程。Goerg G给出了ForeCA的最优化问题[6]：

(6)

s.t.wTΣXw=1

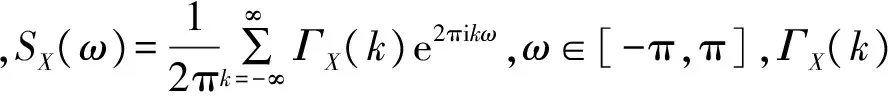
文献[6]给出了求解式(5)的详细算法。通过该算法可以计算出一组按照可预测度由高到低顺序排列的可预测元(可预测元个数可以指定，一般不大于平稳过程的变量个数)，可预测元之间相互正交，由此即可得到线性变换矩阵WT。

3 基于MCUSUM-ForeCA的故障检测

首先选取一段正常工况生成的观测数据Yn×m，其中n为变量个数，m为采样点数(时间序列)，并假设Yn×m中的数据已经经过标准化处理。此时对Yn×m进行MCUSUM处理，定义t时刻的累积和为：

(7)

其中d表示累积和的步数，yi表示第i个时刻的采样值。经过上述处理后产生新的数据矩阵Xn×m。对Xn×m运用ForeCA算法，选取可预测元的个数等于观测数据中变量的个数n，使用算法后得可预测元wi∈Rn,i=1,2,…,n，每个可预测元wi对应的可预测度为Ωi，进而得到线性变换矩阵：

WT=[w1,w2,…,wn]T∈Rn×n

WTW=In∈Rn×n

(8)

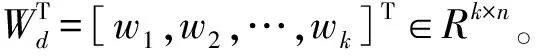
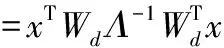
(9)

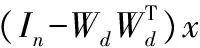
(10)

其中Λ为由前k个可预测元对应的可预测度所组成的对角阵。L2统计量是通过可预测模型内部的可预测元模的波动来反映系统的变化情况，SPE统计量则表示到可预测模型空间的距离，反映了测量值对模型的偏离程度。

根据统计量的公式计算过程正常运行下各采样点的L2值和SPE值后，由于它们并不一定严格的服从正态分布，因此采用核密度估计法[9]对其进行密度估计，密度函数可按下式进行估计：

(11)

其中m是L2值和SPE值的个数；K(·)是核函数，这里选择高斯核函数；h是带宽，使用固定带宽算法计算得到。获得统计量的密度函数后，即可确定L2统计量和SPE统计量的控制限。

当把上述统计量用于在线监控时，首先使用MCUSUM对在线数据进行处理，用于累积过程的历史信息，然后将经过MCUSUM处理后的在线数据代入L2统计量和SPE统计量的表达式中，计算出L2值和SPE值，最后把得到的结果与控制限进行比较，若高于控制限，则说明系统发生故障；若低于控制限，则表示系统运行正常。

4 TE平台仿真实验

TE实验平台[10]由Downs J J和Vogel E F于1993年提出。TE过程(图1)是一个仿真实例，是基于实际工业过程的，可以很好地模拟现实中的复杂工况，因此被广泛地应用在故障诊断领域。

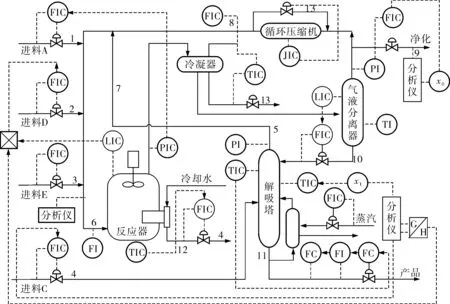
图1 TE过程流程

选取正常的样本数据500个，每个样本点包含33个变量，其中33个变量分别为22个连续变量XMEAS(1)～XMEAS(22)和11个控制变量XMV(1)～XMV(11)，变量的具体含义参见文献[10]。测试数据集包含960个样本点，每个样本点包含33个变量。前160个样本点为正常数据，后800个样本点为故障数据。将MCUSUM-ForeCA方法和传统PCA方法进行对比，在PCA法中，选取T2统计量与SPE统计量。由于MCUSUM中的步长d对检测结果有很大影响，因此笔者在此分两步进行讨论。

首先考虑d为固定值时的情况，选取d=250。图2、3为MCUSUM-ForeCA和PCA方法对TE过程中的故障9和故障15的故障检测对比图。

a. MCUSUM-ForeCA方法

b. PCA方法

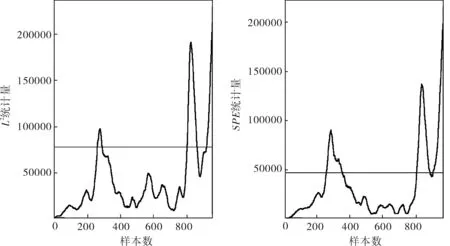
a. MCUSUM-ForeCA方法

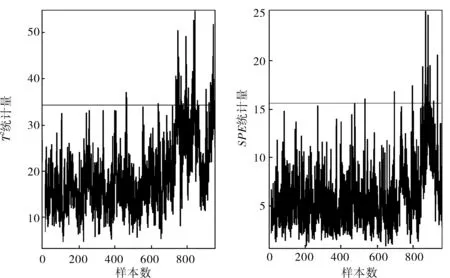
b. PCA方法

故障9是由D的进料温度发生变化导致的，正常工况下和故障状态下变量的均值和方差并未发生明显的变化，属于TE过程中的微小故障。由图2可以看出PCA方法的T2统计量和SPE统计量基本上是无法检测出故障9的，并且在系统正常运行阶段还存在一定的误报率，分别达到了5.0%和1.9%，而MCUSUM-ForeCA的L2统计量和SPE统计量则在390～520个采样点之间持续成功地检测到故障，并且两者的误报率都为0。

故障15是由冷凝器冷却水阀门粘滞导致的，也属于TE过程中的微小故障。由图3中可以看出PCA方法的T2统计量和SPE统计量只是在750个采样点后偶尔检测出故障15，而MCUSUM-ForeCA的L2统计量和SPE统计量则在260～330个采样点之间和800～960个采样点之间持续地检测到故障，并且两者的误报率都为0。

表1列出了两种方法对故障9和故障15的检测准确率。从表1中可以看出，PCA方法的T2统计量和SPE统计量对微小故障的检出率非常低，最高检出率仅有6.0%。而MCUSUM-ForeCA方法的L2统计量和SPE统计量对微小故障的检出率达到了30.0%左右，远高于PCA方法。由此可以看出在对微小故障的检测中，MCUSUM-ForeCA方法显示出了良好的性能。

表1 MCUSUM-ForeCA和PCA的故障 检测准确率比较 %

现在考虑步长d的变化对微小故障检测效果的影响。图4显示了采用MCUSUM-ForeCA方法步长d对故障9和故障15检测准确率的影响。

图4 步长d对故障9和故障15的检测准确率的影响

由图4中可以看出，随着d的增大，故障检测率呈现出波动式上升的趋势。对于故障9，L2统计量在d=260时获得最大检测率37.5%，SPE统计量在d=280时获得最大检测率35.5%；对于故障15，L2统计量在d=260时获得最大检测率25.6%，SPE统计量在d=250时获得最大检测率30.3%。当d的取值较小时，对微小故障的检测准确率较低，因为此时利用MCUSUM得到的历史信息不够丰富，对系统的微小变化的累积效果不明显；当d的取值过大时，一方面累积的历史信息趋于饱和，另一方面累积的过程中会带入部分噪声信息，反而会导致故障的检测效果下降。因此从整体看，d的取值在250～280之间效果比较好。目前从总体来看，d值的选取并没有统一的标准，一般更多的是凭借经验或者交叉验证的方式来选择。

5 结束语

笔者针对传统多元统计方法对过程的微小变化不敏感，无法反映过程时序特性的缺点，将MCUSUM与ForeCA方法相结合，选取可预测主元，构造新的统计量，建立了完整的基于MCUSUM-ForeCA的微小故障检测方法。MCUSUM可用于累积过程的微小变化，ForeCA方法可以更加精确地描述系统的动态特性，因而具有较好的对微小故障的检测能力。最后在TE过程上的仿真结果表明MCUSUM-ForeCA方法的可行性和有效性。但是该方法也存在不足，由于方法中使用了MCUSUM，相应地会在检测过程中产生一定的延时，因此对于某些实时性要求较高的场合，应当考虑将该方法和其他的方法相结合，保证过程安全稳定的运行。

[1] Kimura D,Nii M, Yamaguchi T,et al.Fuzzy Nonlinear Regression Analysis Using Fuzzified Neural Networks for Fault Diagnosis of Chemical Plants[J].JACIII,2011,15(3): 336～344.

[2] Zhang Y W,Zhang Y.Fault Detection of Non-Gaussian Processes Based on Modified Independent Component Analysis[J]. Chemical Engineering Science,2010,65(16):4630～4639.

[3] Kano M, Tanaka S, Hasebe S,et al.Monitoring Independent Components for Fault Detection[J]. AIChE Journal, 2003, 49(4): 969～976.

[4] Wise B M, Ricker N L, Veltkamp D F, et al.A Theoretical Basis for the Use of Principal Component Models for Monitoring Multivariate Processes[J]. Process Control and Quality,1990,1(1): 41～51.

[5] Pignatiello J J, Runger G C. Comparisons of Multivariate CUSUM Charts[J].Journal of Quality Technology, 1990, 22(3): 173～186.

[6] Goerg G.Forecastable Component Analysis[C].Proceedings of the 30th International Conference on Machine Learning.Atlanta, USA:ICML,2013: 64～72.

[7] Shannon C E. A Mathematical Theory of Communication[J].ACM SIGMOBILE Mobile Computing and Communications Review,2001,5(1):3～55.

[8] Kohavi R. A Study of Cross-validation and Bootstrap for Accuracy Estimation and Model Selection[C].Proceedings of the 14th International Joint Conference on Artificial Intelligence.San Francisco,USA:Morgan Kaufmann Publishers Inc，1995:1137～1145.

[9] Wand M P, Jones M C. Kernel Smoothing[M]. Boca Raton: Crc Press,1994.

[10] Downs J J,Vogel E F.A Plant-wide Industrial Process Control Problem[J].Computers & Chemical Engineering,1993,17(3):245～255.