基于S变换的配电网高阻抗故障检测方法研究

李梦达 段玉波 刘铁良 王 勇

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

高阻抗故障(HIF)含有丰富的电流谐波分量，主要分为主动故障和被动故障。主动故障的电弧和当前电流低于保护继电器的极限，电流通常会逐渐衰减直至电弧消失[1]，大多数主动故障检测技术都是利用电弧产生的信号，但在检测系统确认故障之前电弧就会消失，不能有效检测故障；被动故障虽然不会产生电弧，但由于没有交流供能导体会更加危险，因此在HIF中电流很低或者没有时，传统的过电流保护系统通常会检测失败。

Sedighi A R等提出了结合小波变换和软计算应用分类的方法检测HIF[2]，但由于小波变换对噪声的抑制效果较差，即使信噪比达到30db，结果也会存在很大的误差。Sharaf A M和El-Sharkawy R M采用了人工神经元组的方法检测HIF，虽然系统能够准确地识别标准信号，但因模糊神经网络对系统频率的变化需要大量的数据和长期的训练时间，故其在高频率信号中很难得到较好的应用[3]。上述文献所采用的检测方法均具有一定的局限性。

笔者通过S变换处理故障与无故障(NF)的电流信号，在较高的频率分辨率和较低的时间分辨率下获得准确的频率信息，在较高的时间分辨率和较低的频率分辨率下获得准确的时间信息，继而利用非线性负载条件下的HIF电流信号特征点来训练和测试神经网络，使其能够区分HIF与NF事件。

1 系统研究①

以三相径向配电馈线模型为例，在Matlab平台上搭建其仿真模型(图1)。由一个电压为15kV、容量为10MVA的发电机连接一个15/25kV、10MVA的变压器，分布网络运行在25kV的电压下。仿真模型采用了电力系统Blokset模型，采样频率选择1.0kHz。HIF在线性负载条件下的电流如图2所示。从图2可以看出HIF出现在1/2个正常的周期后，且与无故障前的电流信号相比含有更高的谐波分量，因此在线性负载条件下，提取谐波成分可以很容易地区分出HIF和NF。但在非线性负载条件下，故障后的电流和无故障的电流都含有较高的谐波分量，很难区分HIF和NF，在电力分布网络中这是个至关重要的问题。笔者将针对非线性负载条件下的电流信号进行分析。

2 S变换的概念

S变换是连续小波变换和短时傅立叶变换的组合与扩展，是一种可移动、可伸缩的高斯窗函数[4]。S变换属于广泛多分辨率的频谱分析，由于其标准偏差是一个逆函数的频率，因此减少了维度的运算[5]。高斯函数g(t)的表达式为：

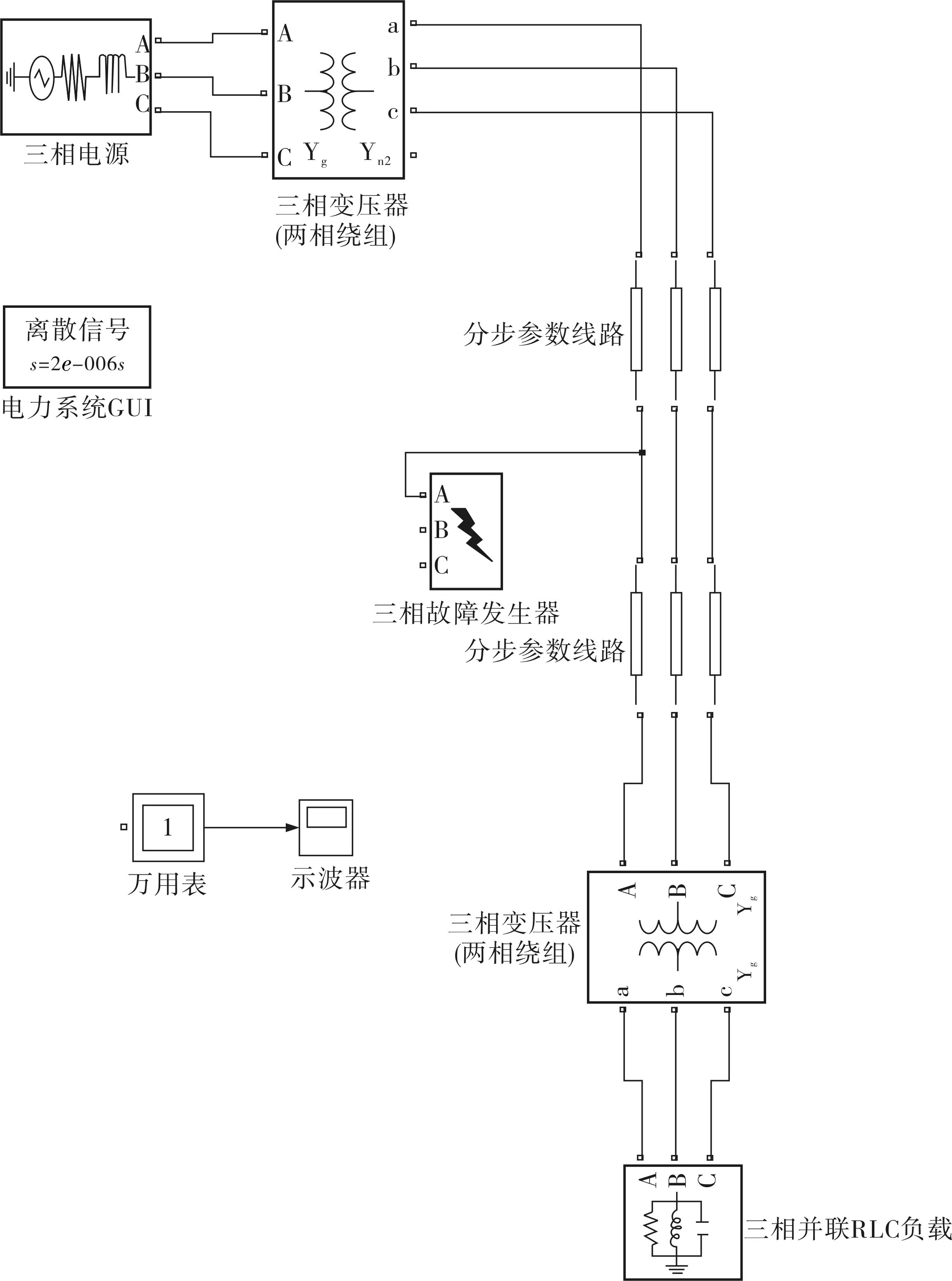
图1 三相径向配电馈线仿真模型

图2 HIF在线性负载条件下的电流(A相)

(1)

其中，σ为标准偏差。则S变换定义为：

(2)

S变换是多分辨率的傅里叶变换，扩展参数的主要目的是提高窗函数的宽度，进而降低频率，反之亦然[6,7]。笔者选择窗的宽度与频率的绝对值成反比，即：

(3)

其中，T为周期，统一选为常数。式(3)使高斯窗在最窄的时间域内。S变换可以写成：

(4)

从式(4)可以看出，零频率的S变换等同于零，没有任何信息，因此S(f，τ)是时间独立的，并等于函数h(t)的平均值，即：

(5)

对于离散S变换，h(t)可以写成h[pT]离散形式，此时p在[0，N-1]之间变化，并是信号h(t)的离散时间序列。离散傅里叶变换的时间系列h[pT]可以表示为：

(6)

其中，n∈[0，N-1]。离散傅里叶逆变换形式为：

(7)

离散S变换是时间序列h[pT]向量集合的投影。由于生成的向量集合非正交，且S矩阵的元素不相关，基本向量一个接一个被分进N维局部向量中来改变高斯分布，因此N维局部向量之和是原始的基本向量。S变换的离散时间序列H[pT]表示为：

(8)

其中，j、m、n=0，1，2，…，N-1。当n=0时：

(9)

3 基于S变换的特征提取

在电力分布网络中时频转换被认为是利用S变换提取HIF和NF不同操作条件下的电流信号特征，提取的特征点是故障后半个周期的电流信号。HIF和NF的电流信号是通过设计配电模型生成的，相应电流信号的频率信息和时间信息可从生成的S矩阵以适当的频率和时间分辨率提取。

从S矩阵中提取的频率信息为：

a=max(abs(ST))

(10)

其中，a表示S变换后转置矩阵的最大绝对值，它提供了幅频信息。同样，从S变换中提取时间信息为：

b=max(abs(S))

(11)

其中，b表示S变换后矩阵的最大绝对值，它提供了时间的振幅信息。电能和标准偏差的频率和时间信息分别为：

P(f)=sum(a2)

(12)

σ(f)=std(a)

(13)

P(t)=sum(b2)

(14)

σ(t)=std(b)

(15)

频率信息在较高的频率分辨率和较低的时间分辨率情况下提取；时间信息在较高的时间分辨率和较低的频率分辨率下提取。图3、4分别给出了在HIF和NF的电流信号时间样本和频率的关系，并对信号的时频聚集性进行了比较，其中，短时振幅特性反映了时间信息，级对频率特性反映了频率信息。

图3 HIF情况下的电流信号S变换

图4 NF情况下的电流信号S变换

通过比较图3、4可以看出，S变换能够提取非线性负载条件下HIF的信号特征，且该信号特征能够用于概率神经网络和模糊神经网络中进行故障分类，最终区分HIF和NF。

4 结束语

介绍了HIF的智能检测技术，并试图在非线性负载条件下区分HIF和NF。HIF和NF电流信号的时频分布用S变换进行提取，可快速而准确地识别NF和HIF，同时，该方法可扩展应用到大型配电网络的保护方法中。

[1] 肖湘宁，徐永海.电能质量问题剖析[J].电网技术，2001，25(3)：66～69.

[2] Sedighi A R, Haghifam M R, Malik O P. Soft Computing Applications in High Impedance Fault Detection in Distribution Systems[J]. Electric Power Systems Research, 2005,76(1/3):136～144.

[3] Sharaf A M, El-Sharkawy R M. Novel Alpha-transform Distance Relaying Scheme[C]. Canadian Conference on Electrical and Computer Engineering.Alta: IEEE,1996: 754～757.

[4] 全惠敏，戴瑜兴.基于S变换模矩阵的电能质量扰动信号检测与定位[J].电工技术学报，2007，22(8)：119～125.

[5] 刘守亮，肖先勇，杨洪耕.基于S变换模时频矩阵相似度的短时电能质量扰动分类[J].电网技术，2006，30(5)：67～71.

[6] Yang H T, Liao C C. A De-noising Scheme for Enhancing Wavelet-based Power Quality Monitoring System[J]. IEEE Transactions on Power Delivery, 2001, 16(3):353～360.

[7] Pinnegar C R, Mansinha L. The S-transform with Windows of Arbitrary and Varying Shape[J]. Geophysics, 2003, 68(1):381～385.