基于改进MRAS 观测器的感应电动机转速估算方法
2015-01-13蔡文皓
蔡文皓,王 超,罗 强
(西安科技大学,西安710054)
0 引 言
感应电动机矢量控制系统通常采用加装编码器来检测转速,然而高精度的编码器不仅价格昂贵,增加整体系统的成本,而且提升系统本身的复杂度,故近年来越来越多的国内外学者投入到无转速传感器矢量控制的研究中。目前的研究方法大致有:基于电机模型的直接计算法;模型参考自适应(以下简称MRAS)法;扩展卡尔曼滤波法;高频信号注入法;滑模变结构法等。文献[1]~[5]分别对这几种方法进行了较详细的介绍。其中,基于MRAS 的转速估算模型具有算法简单,易于实现,有较好的鲁棒性,现已被广泛应用于无速度传感器感应电动机交流调速系统中。但由于在传统MRAS 中,转速是否能估算准确,很大程度上是由所选取的参考模型的精确度决定,并且模型容易受电机在运转过程中参数的变化所影响,尤其是在低速下。所以很多MRAS 算法中都加入了电机参数的在线辨识,这无疑增加了算法的复杂度。故本文基于传统MRAS方法,提出一种改进的参考模型,不需要在线辨识电机参数,感应电动机无转速系统也能在低速下准确估算转速,使系统稳定运行,并通过在MATLAB 中建立改进模型后的感应电动机无速度传感器矢量控制仿真验证有效性。
1 传统MRAS 结构
传统的MRAS 结构主要分为三个部分,分别为参考模型、可调模型以及自适应率,其中参考模型不包含带估计参数,并且认为参考模型是理想的模型,由它表示的电动机状态与实际相符。将包含转速信息的待估计参数模型作为可调模型。要求参考模型与可调模型有相同的外部输入,且两模型的输出是具有相同物理意义的变量。通过比较,将差值传入自适应率,进而调整可调模型中的估算转速,使得两模型的输出误差在稳态时趋向于零。此时即可认为可调模型中待估计的速度,为当时电机运转的速度。传统MRAS 的基本结构如图1 所示。
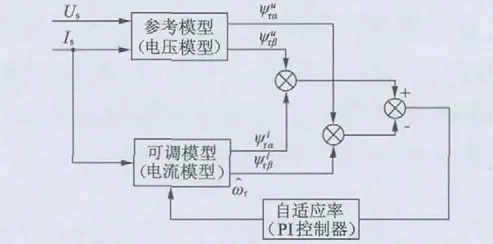
图1 传统MRAS 系统结构图
通常选择基于定子电压和电流,在两相静止坐标系下的转子磁链的电压模型作为参考模型。
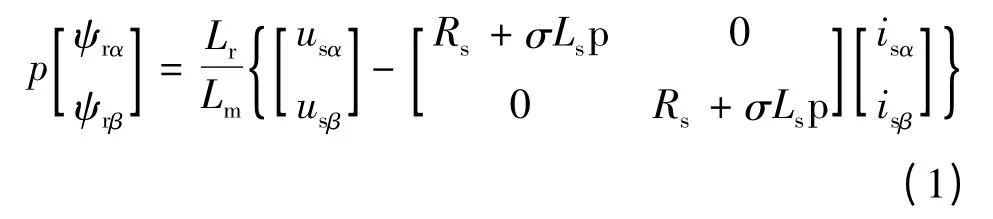
选择基于定子电流和转速估计值,在两相静止坐标系下的转子磁链的电流模型作为可调模型。
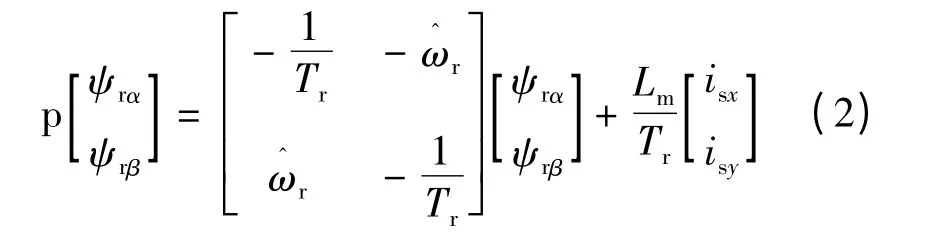
取两模型输出磁链的误差作为自适应率的输入,这里采用两相静止坐标系下的广义误差,即:
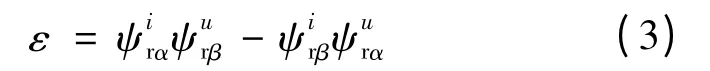
转速自适应率为PI 控制器,输出即估算出的转速,再反馈给电流模型,进一步调整其模型中转速变量。当两模型输出磁链相等时,认为电流模型估算磁链准确,则模型中的转速变量即为当时转速:
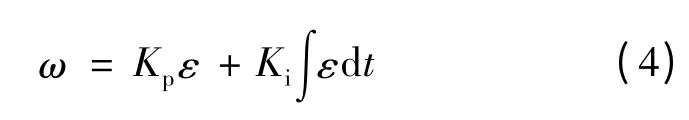
2 改进的电压型转子磁链估算模型
在实际应用中,由于定子电阻温升引起的阻值变化,以及低速时定子电阻压降作用明显,使得反电动势受测量误差影响变大,观测精度降低。当定子电阻变化ΔR 时,转子磁链变为:
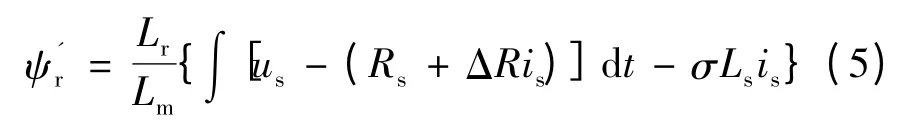
若此时仍按原阻值估算转子磁链,则:
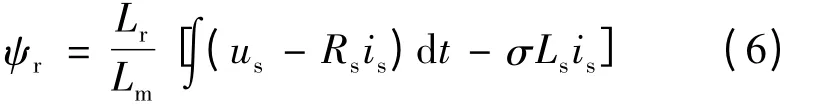
因此,由定子电阻变化引起的转子磁链估算误差:
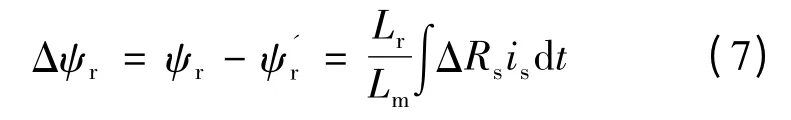
显然,式(7)特征根为0,观测误差不收敛[6]。故本文基于定、转子磁链关系,引入定子电流的补偿部分,改进了传统的电压参考模型,传统MRAS 与改进MRAS 参考模型结构图分别如图2 所示。
改进参考模型转子磁链计算如下:
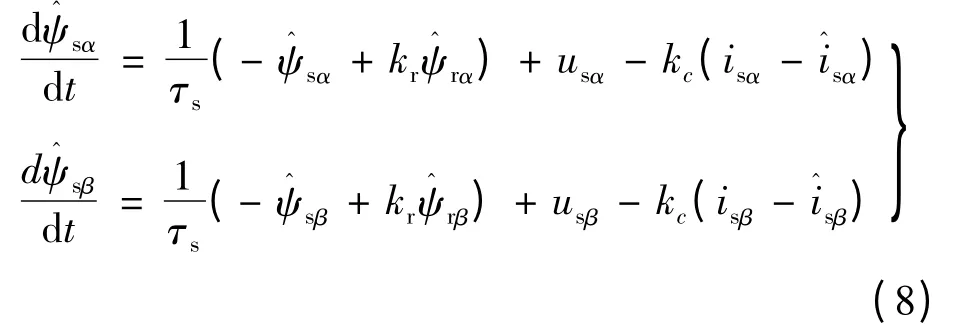
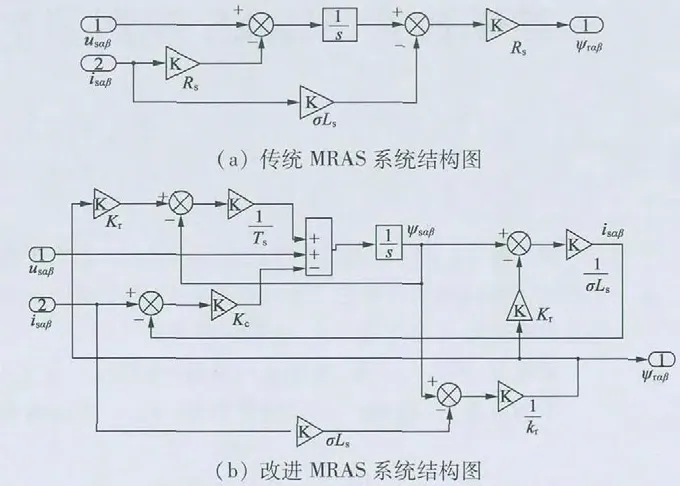
图2 MRAS 系统结构图
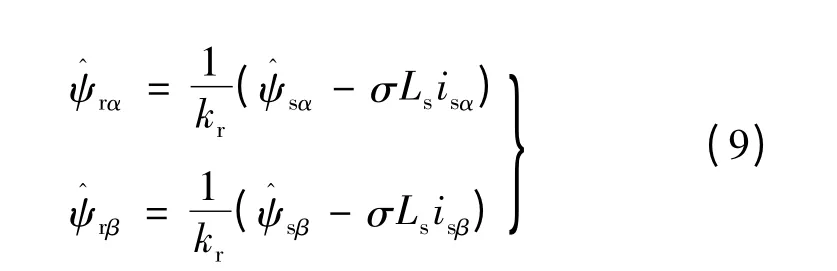
当反馈补偿部分isα(β)与,即两相静止坐标系下,实际的定子电流与估算的定子电流误差为零时,式(8)经化简即为传统电压模型转子磁链关系式。估算的定子电流由下式获得:
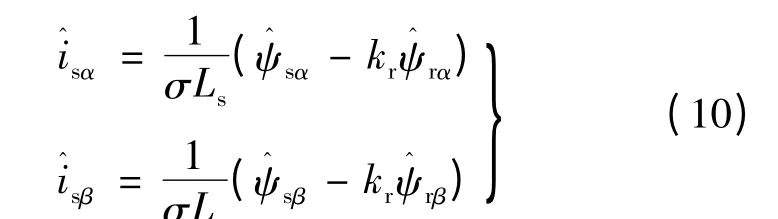
在计算转子磁链时所用到的电机参数为定子电感、转子电感、互感以及定子电阻。由于电机对电感的变化并不敏感,而且在零频附近,定子电阻的变化也对观测器的输出磁链几乎没有影响[7]。改进后的参考模型仍旧不需要转速信息,由模型框图可以看出,通过常数kc与定子电流误差的积形成的负反馈,动态补偿模型在计算磁链时的误差,增加了观测器的鲁棒性,使得感应电动机在较大运行范围内仍旧能保持系统的稳定,不但不需要在线辨识系统参数,而且消除了传统参考模型中的直流偏置和检测信号时所带来的误差。
3 仿真验证
为了验证前述方法的正确性与可行性,在MATLAB/Simulink 中搭建本系统仿真模型,并进行仿真。所采用异步电机额定参数:Pn=3 kW,Un=380 V,fn=50 Hz,p =2,Rs=1.798 4 Ω,Rr=1.588 Ω,Ls=0.007 3 H,Lr=0.007 7 H,Lm=0.387 H。
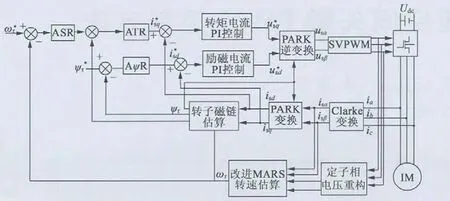
图3 感应电动机无转速传感器矢量控制系统
如图3 所示,整个系统由逆变器、电机、转速与磁链辨识等部分组成,为电流内环、转速与磁链闭环的矢量控制系统。运行时,首先检测电机三相定子电流isa,isb,isc,经过坐标变换,得到isα,isβ和id,iq,将isα,isβ与由逆变器直流母线电压和逆变器开关量重构得到的定子相电压usα,usβ输入改进MRAS 模型中得到估算转速,由估算转速ω^与id,iq进一步估算转子磁链,最后将估算的转速与磁链跟给定转速与磁链比较后,经转速环与磁链环的PI 调节器进行动态调整,并控制SVPWM 作出相应变化,估算值跟随给定值,系统得以稳定运行。
图4、图5 分别为电机给定磁链1 Wb,空载起动,0.5 s 后突加10 N·m 负载运行,给定转速100 rad/s 和3 rad/s(定子电阻升高50%)时的仿真结果。
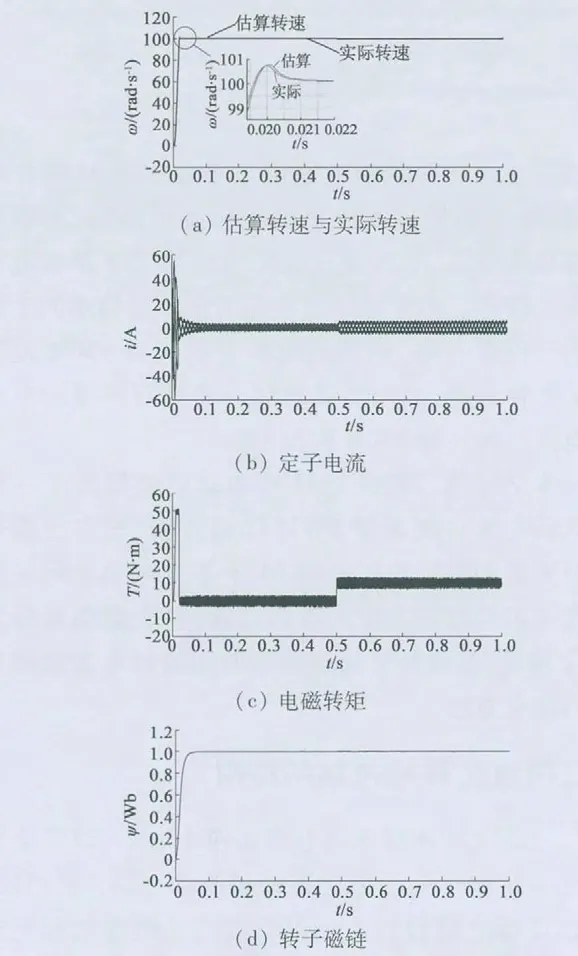
图4 电机给定转速100 rad/s
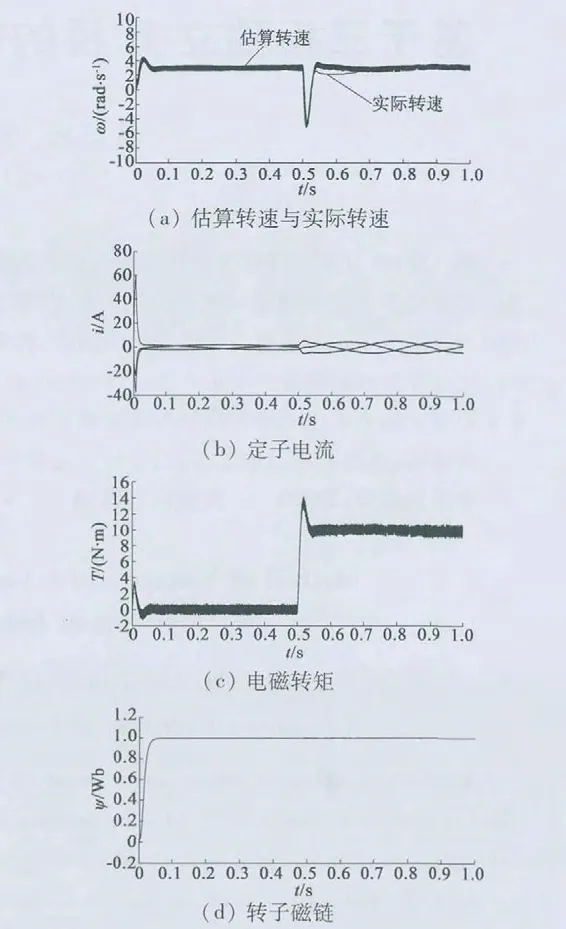
图5 电机给定转速3 rad/s(定子电阻升高50%)
从图4、图5 可以看出,不论运转在高速下还是低速下,电机都能较快进入稳态,估算转速与实际转速之间的误差较小,0.5 s 后突加负载,系统仍能克服扰动,输出10 N·m 转矩并稳定运行。而且即便在低转速下定子电阻升高50%,改进参考模型后的MRAS 观测器对这种变化仍具有较好的抗干扰能力,转速与转矩跟随性好,波动小,系统运行稳定,肯定了改进的MRAS 观测器的有效性。
4 结 语
本文提出一种基于改进MRAS 观测器的感应电动机转速估算方法,选择改进型电压模型作为参考模型,通过建立定子磁链与转子磁链的关系,并引入定子电流作为磁链计算的负反馈,尤其是在低速下,避免了电机参数变化所造成的磁链计算误差,可不需要在线辨识电机参数。最后通过建立MATLAB仿真,验证改进模型下的感应电动机无速度传感器矢量控制具有较好的暂稳态性能,鲁棒性强。
[1] 王成元,夏加宽,孙宜标.现代电机控制技术[M].2 版. 北京:机械工业出版社,2014.
[2] 罗龙,杜峰,谢刚.基于典型MRAS 无速度传感器矢量控制系统的改进研究[J].绵阳师范学院学报,2011,30(5):35-43.
[3] 武卯泉.基于EKF 和改进MRAS 的转速估计研究[D]. 成都:西华大学,2008.
[4] 冬雷,李永东.无速度传感器异步电机极低转速下的矢量控制[J].清华大学学报,2003,43(9):1169-1172.
[5] 朱瑛,程明,花为,张邦富,王伟. 基于滑模变结构模型参考自适应的电气无级变速器无传感器控制[J]. 电工技术学报.2015,30(2):64-72.
[6] 朝泽云.无速度传感器矢量控制系统的若干问题研究[D].武汉:华中科技大学,2006.
[7] PELLEGRINO G,BOJOI R I,GUGLIELMI P,et al. Accurate Inverter Error Compensation and Related Self - Commissioning Scheme in Sensorless Induction Motor Drives[J]. IEEE Transactions on Industry Applications,2010,46(5):1970-1978.
[8] GUZINSKI J,ABU-RUB H.Predictive current control implementation in the sensorless induction motor drive[C]/ /IEEE International Symposium Industrial Electronics,2011:691-696.
