Steering Vibrational Population Transfer via Double-Σ-Type Laser Scheme

Li-hang Li,Yong-chang Han,Shu-lin Cong

School of Physics and Optoelectronic Technology,Dalian University of Technology,Dalian 116024, China

Steering Vibrational Population Transfer via Double-Σ-Type Laser Scheme

Li-hang Li,Yong-chang Han∗,Shu-lin Cong

School of Physics and Optoelectronic Technology,Dalian University of Technology,Dalian 116024, China

The vibrational state-selected population transfer from a highly vibrationally excited level to the ground level is of great importance in the preparation of ultra-cold molecules.By using the time-dependent quantum-wave-packet method,the population transfer dynamics is investigated theoretically for the HF molecule.A double-Σ-type laser scheme is proposed to transfer the population from the|v=16〉level to the ground vibrational level|v=0〉on the ground electronic state.The scheme consists of two steps∶The frst step is to transfer the population from|v=16〉to|v=7〉via an intermediate level|v=11〉,and the second one is to transfer the population from|v=7〉to|v=0〉via|v=3〉.In each step,three vibrational levels form a Σ-type population transfer path under the action of two temporally overlapped laser pulses.The maximal population-transfer efciency is obtained by optimizing the laser intensities,frequencies,and relative delays.Cases for the pulses in intuitive and counterintuitive sequences are both calculated and compared.It is found that for both cases the population can be efciently(over 90%)transferred from the|v=16〉level to the|v=0〉level.

Population transfer,Wave packet dynamics,Vibrational state

I.INTRODUCTION

Preparation of specifc quantum states is a widely concerned subject in the atomic and molecular physics, quantum information and other felds[1−3].In both theory and experiment,various techniques including optimal control,multi-channel technology,adiabatic channel technology have been proposed[4−8].As one of the most efcient techniques,stimulated Raman adiabatic passage(STIRAP)has been investigated extensively[9, 10].STIRAP can realize high efciency of population transfer with properly overlapped laser pulses in counterintuitive sequence.Here,the phrase,“counterintuitive sequence”,means that the laser pulse connecting the intermediate state with the target state comes before and overlaps with the laser connecting the intermediate state with the initial state.In the two-photon resonance conditions,the adiabatic passage is formed by adjusting the intensity,duration of the laser pulse, and delay time.By properly setting the laser parameters,the population can be transferred from the initial state to the target state via an adiabatic passage without residual on the intermediate state during the whole process.

There have been great progresses in the studies and applications of STIRAP these years.Vitanov and Shore created maximally coherent superposition in a two-state atom by adiabatic passage,and they found the method was robustly insensitive to minor changes in pulse properties[11].Drummondet al.studied the realization of the coherent molecular Bose-Einstein condensation (BEC)from an atomic BEC by STIRAP.They identifed the most appropriate way to maintain high conversion efciencies[12].The STIRAP technique has also been extended to achieve coherent control of population transfer via ionization continuum[13,14].More recently,it is proposed that by using the combination of the Feshbach resonance and the STIRAP technique, one can create ultra-cold molecules[15,16].

Most of coherent control studies of population transfer focused on the excitation process from a lower state to an upper state.We are motivated by the fact that in the processes of photoassociation driven by infrared (IR)laser felds,the collision atomic pair usually associates into a molecule on a highly vibrationally excited level of the ground electronic state[17−23].Thus,to transfer the molecular population from such an energetic level to the ground vibrational level is of potential application.Based on this“upper-to-lower”population transfer process,one can increase the rate of the photoassociation and the creation of the ultra-cold molecules.

In this work,we take the HF molecule as a model system to propose a control scheme for the achievement of efcient“upper-to-lower”population transfer.Liuet al.recently investigated the photoassociation of H+F→HF and obtained a high product yield of the HF molecule on the|v=16〉state[23].We then take the|v=16〉state as the initial state and introduce an efcient laser scheme

In each step,three relevant vibrational levels form a Σ-type population transfer path under the action of two temporally overlapped laser pulses,i.e.,E0(2)andE1(3).To investigate the feasibility of this double-Σ-type scheme,we perform calculations for two cases according to the sequence of the two pulses involved in each Σ-type step.We frst consider the two pulses in each step to be in counterintuitive sequence(case I),which may lead to STIRAP-like population transfer process,and then consider the two pulses in step II to be in intuitive sequence(case II).

In this work,using the theoretical method,we demonstrate the determination of the intermediate states,and present the results under the action of the double-Σ-type laser scheme for cases I and II.The two cases are compared and discussed in detail.

II.THEORETICAL TREATMENTS

The vibrational wave function of the HF molecular on the ground electronic state under the interaction of the laser pulses can be obtained by solving the timedependent Schr¨odinger equation

whereˆTdenotes the kinetic energy operator andˆV(R) denotes the potential energy operator.Invoking dipole approximation,ˆW(R,t)can be expressed as

whereµ(R)denotes the permanent dipole moment.The relevant expressions and parameters forV(R)andµ(R) are taken from Ref.[24].E(t)is the electric feld of the laser pulses

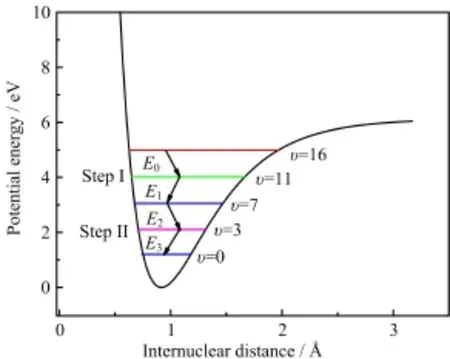
FIG.1 The double-Σ-type scheme for the population transfer from|v=16ito|v=0ion the ground electronic state of the HF molecule.

whereEi,ωi,ti,andτidenote the peak amplitude, center frequency,starting time,and the duration of theith laser pulse,respectively.Note that in this study, we focus on the transition between the vibrational levels while the efect of the rotational motion of the HF molecule on the stimulated transition is neglected.For the discussions of the efect of the molecular rotation on the stimulated transition process,see Ref.[25].

To solve Eq.(1),the initial wave functionψ(R,t=0) is set to be the eigen wave function of|v=16〉,which can be obtained with the Fourier grid Hamiltonian(FGH) method[26],and then the wave function at a given timetcan be obtained by short-time propagation with the split-operator method[27]∶

The populationPm(t)on a specifc vibrational states|v=m〉at timet,can be calculated with the projection operation,

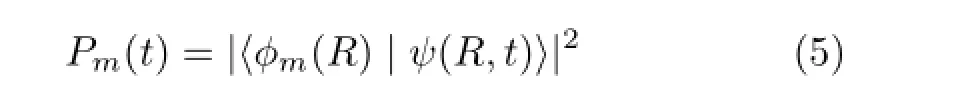
whereφm(R)is the eigen wave function of the|v=m〉state obtained via FGH method[27].

In addition,in order to determine proper vibrational levels to serve as the intermediate states,we calculated the following overlap integrals for two selected vibrational levels,|v=n〉and|v=m〉,

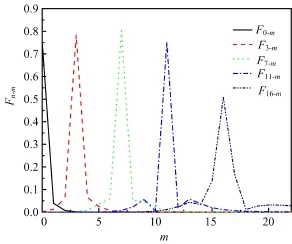
FIG.2 TheFn-mfactor forn=0,3,7,11,and 16,respectively,andmvaries from 0 to 22.

Actually,the factorFn−mis the absolute square of the transition dipole moment between the two given vibrational levels,|v=n〉and|v=m〉,and it denotes the coupling strength between the two levels.The quantum numbers,nandm,vary in[0,23],because the maximal vibrational quantum number for the HF molecule is 23[23].

III.RESULTS AND DISCUSSIONS

A.Determination of the intermediate states

The intermediate states,which connect the initial vibrational level|v=16〉with the target level|v=0〉,are determined by the calculations of theFn−mfactors defned by Eq.(6).TheFn−mfactors forn=0,3,7,11, and 16,respectively,are shown in Fig.2,withmvarying from 0 to 22.It can be seen that the coupling of|v=n〉with|v=m〉via the permanent dipole moment, becomes weaker with the increase of the diference between the two quantum numbers.The strongest transition always occurs between|v=n〉and|v=n±1〉,and this is consistent with the basic transition law of the diatomic molecules.Moreover,the overtone transitions can also occur due to the anharmonicity of the potential energy curve,although the transition probability is rather weak.

It is worth noticing that the number of intermediate states is expected to be small to avoid the midway loss of the population and to reduce the number of the laser pulses used for control.Thus,we select|v=3〉,|v=7〉,|v=11〉to be the intermediate states,which construct a double-Σ-type transition path connecting|v=16〉with|v=0〉.To investigate the feasibility of this double-Σ-type scheme,we consider the following two cases.In case I,we set the two pulses to be in counterintuitive sequence for both steps,and in case II,we keep the pulse sequence in the step I to be counterintuitive but change that in step II to be intuitive.We will show that by properly choosing the laser parameters,an effcient population transfer probability can be obtained for both cases.In the calculations,for each case,the photon energy is set to be resonant with the energy difference between neighboring levels,while the other laser parameters are varied to obtain an optimized population transfer probability.Specifcally,the pulse duration varies from 1 ps to 7 ps with an interval of 100 fs, the time delay between two pulses in each step varies from 0 fs to 500 fs with an interval of 10 fs,and the peak intensity of the electric feld for each pulse varies from 0.005 a.u.to 0.03 a.u.with an interval of 0.0005 a.u. The optimized population transfer probabilities for the two cases are shown and discussed in detail in the following subsections,respectively.

FIG.3 The temporal envelopes of the electric felds of the four pulses used in case I.

TABLE I The relevant parameters of laser pulses used for case I.

B.Case I:counterintuitive pulse sequence for both steps

The temporal profles of the optimized electric felds of the four pulses used in case I are shown in Fig.3,and the corresponding laser parameters are listed in Table I. The two pulses in each step are assigned in counterintuitive sequence.Pulse 0(E0)is switched on 200 fs later than pulse 1(E1)for step I,and pulse 2(E2)is 50 fs later than pulse 3(E3).The peak intensities for the pulses used in step II are more intense than those used in step I,since the factorsF3−0andF3−7for step II are smaller thanF7−16andF7−11for step I.The evolution of the population among the fve levels under the actionof such external felds is shown in Fig.4.For each step, the population transfer occurs during the overlapping time interval of the two relevant pulses.After the action of the laser feld,roughly 94%of the population has been transferred to|v=0〉.

Although the total loss of the population is rather small,the|v=7〉state plays a dominant role for the loss out of the three intermediate states.This is because the|v=7〉state connects the two Σ-type steps,while in each Σ-type step,the sub-intermediate state|v=11〉(or|v=3〉)serves somewhat like the dark state used in the conventional STIRAP scheme.As seen in Fig.4,roughly 98%of the population can be temporarily transferred to|v=7〉,while the maximal values for the temporary population on|v=3〉and|v=11〉are both less than 60%. We should note that it is not a real STIRAP process for each step.It requires even more intense lasers to overcome the weak overtone transition dipoles and to form the real adiabatic passages,however,on the other side of the coin,the intense laser would lead to unwanted excitations of the molecules.Therefore,we set the laser intensities to be mildly intense,and set the delay times between two pulses involved in a certain step to be much shorter than the pulse durations.With this set of laser parameters,one can reduce the losses from the sub-intermediate states|v=3〉and|v=11〉,while the loss should mainly comes from the|v=7〉state.

The spacial distribution function,|ψ(R,t)|2,propagating with time are shown in Fig.5 as a contour plot. Initially,we can see a clear distribution of the eigenstate|v=16〉.With the evolution of time,the distribution merges to be that of|v=7〉.Finally,a distribution for the|v=0〉state is easily distinguishable.From this point of view,it also indicates that the intermediate state|v=7〉plays a more important role with respect to the other two intermediate states,because one can hardly observe the distributions of the|v=3〉and|v=11〉states from Fig.5.

FIG.4 The evolution of population on the relevant vibrational levels for case I.

FIG.5 The evolution of the spacial distribution function,|ψ(R,t)|2.

FIG.6 The temporal envelopes of the electric felds of the four pulses used in case II.

C.Case II:counterintuitive pulse sequence for step I and intuitive sequence for step II

We now consider case II,in which we keep most of the laser parameters to be the same as the optimal values used in case I,but only vary the durations and delay times of the two pulses used for step II.In this case, the two pulses for step I maintain in counterintuitive sequence,while the other two for step II are assigned in intuitive sequence.Pulse 2 is now switched on ahead of pulse 3 by 450 fs,and the duration of pulse 2 are 1 ps shorter than the one used in case I.The laser parameters used for case II can be found in Table II,and the electric-feld profles for the four pulses are shown in Fig.6.

The corresponding population transfer dynamics for case II is shown in Fig.7.Comparing Fig.7 and Fig.4, we found that the corresponding population transfer dynamics for step I are almost the same for cases I and II. This is because that the laser parameters for step I in case II is kept to be the same as those used in case I and the infuence of the pulses 3 and 4 on the step I is negligible for both cases.Nevertheless,for step II,the dy-namics presents a little diference between the two cases. The maximal value of the temporary population on the sub-intermediate state,|v=3〉,in case I,roughly 0.57,is smaller than the corresponding value in case II,roughly 0.64.This is because that the counterintuitive pulse sequence used in case I can form a population-transfer passage directly connecting the target state with the initial state.Although this passage formed in case I is not adiabatic due to the mild laser intensities and the relatively large overlap region between pulses 3 and 4,it still can,to some extent,suppress the temporary population on the sub-intermediate state.After the actions of the four pulses,the fnal population transferred to the target|v=0〉state is roughly 95%and 97%for cases I and II,respectively,which are comparably and relatively high.It indicates that with this double-Σ-type scheme and proper laser parameters,the population can be efciently transferred from the high vibrational level to the ground level and this scheme is fexible for both cases.

FIG.7 The evolution of population on the relevant vibrational levels for case II.

TABLE II The relevant parameters of laser pulses used for case II.

IV.CONCLUSION

By taking the HF molecule as a n example,we proposed a double-Σ-type laser scheme to transfer the population from a high vibrational level,|v=16〉,to the ground vibrational level,|v=0〉,on the ground electronic state.The scheme can be divided into two steps∶The frst step is to transfer the population from|v=16〉to|v=7〉via an intermediate level|v=11〉,and the second one is to transfer the population from|v=7〉to|v=0〉via|v=3〉.The feasibility and efciency of this control scheme are investigated by the consideration of two cases concerning about the pulse sequence.Although it is hard to form real adiabatic passages in this control scheme due to the weak overtone transition probability,the loss of the population on the intermediate state can be reduced to a rather small value by properly choosing the laser parameters.For both cases,we obtain efciency population transfer probabilities(over 90%).It could be expected that this scheme might present potential applications for the laser cooling molecules and the coherent control of the molecular quantum states.

V.ACKNOWLEDGMENTS

Li-hang Li thanks Dr.Yin Huang for assistance. The project is supported by the Specialized Research Fund for the Doctoral Program of Higher Education (No.20130041120053),SRF for ROCS,SEM,the Science and Technology Research Funds of the Department of Education of Liaoning Province(L2013014), the National Magnetic Confnement Fusion Science Program(No.2013GB109005),the Fundamental Research Funds for the Central Universities(DUT12RC(3)60), and the National Natural Science Foundation of China (No.21473018,No.10974024,and No.11274056).

[1]H.G.Rubahn and K.K.Bergmann,Annu.Rev.Phys. Chem.41,735(1990).

[2]A.Ekert and R.Jozsa,Rev.Mod.Phys.68,733(1996).

[3]M.Weitz,B.C.Young,and S.Chu,Phys.Rev.Lett.73,2563(1994).

[4]B.M.Garraway and K.A.Suominen,Phys.Rev.Lett.80,932(1998).

[5]L.P.Yatsenko,B.W.Shore,T.Halfmann,K. Bergmann,and A.Vardi,Phys.Rev.A60,R4237 (1999).

[6]V.S.Malinovsky and I.R.Sola,Phys.Rev.Lett.93, 190502(2004).

[7]T.Cubel,B.K.Teo,V.S.Malinovsky,J.R.Guest,A. Reinhard,B.Knufman,P.R.Berman,and G.Raithel, Phys.Rev.A72,023405(2005).

[8]S.D.Clow,C.Trallero-Herrero,T.Bergeman,and T. Weinacht,Phys.Rev.Lett.100,233603(2008).

[9]K.Bergmann,H.Theuer,and B.W.Shore,Rev.Mod. Phys.70,1003(1998).

[10]U.Gaubatz,P.Rudecki,S.Schiemann,and K. Bergmann,J.Chem.Phys.92,5363(1990).

[11]N.V.Vitanov and B.W.Shore,Phys.Rev.A73, 053402(2006).

[12]P.D.Drummond,K.V.Kheruntsyan,D.J.Heinzen, and R.H.Wynar,Phys.Rev.A65,063619(2002).

[13]Y.C.Han,S.M.Wang,K.J.Yuan,and S.L.Cong, Chem.Phys.333,119(2007).

[14]T.M.Yan,Y.C.Han,K.J.Yuan,and S.L.Cong, Chem.Phys.348,39(2008).

[15]L.H.Lu and Y.Q.Li,Phys.Rev.A76,053608(2007).

[16]X.J.Hu,W.Zhang,Y.Huang,J.F.Yang,and S.L. Cong,J.Theor.Comp.Chem.11,1323(2012).

[17]M.V.Korolkov and B.Schmidt,Chem.Phys.Lett.272,96(1997).

[18]E.F.de Lima and J.E.M.Hornos,Chem.Phys.Lett.433,48(2006).

[19]E.F.de Lima,T.S.Ho,and H.Rabitz,Chem.Phys. Lett.501,267(2011).

[20]Y.Y.Niu,S.M.Wang,and S.L.Cong,Chem.Phys. Lett.428,7(2006).

[21]P.Marquetand and V.Engel,J.Chem.Phys.127, 084115(2007).

[22]Y.Y.Niu,R.Wang,M.H.Qiu,and J.L.Xiu,Int.J. Quantum Chem.111,2117(2011).

[23]L.Liu,Y.Y.Niu,K.J.Yuan,S.L.Cong,Chin.Phys. B16,2957(2007).

[24]M.Kaluˇza,J.T.Muckerman,P.Gross,and H.Rabitz, J.Chem.Phys.100,4211(1994).

[25]K.J.Yuan,Z.G.Sun,S.L.Cong,and N.Q.Lou,Phys. Rev.A,74,043421(2006).

[26]C.C.Marston and G.G.Balint-Kurti,J.Chem.Phys.91,3571(1989).

[27]M.D.Feit and J.A.Jr.Fleck,J.Chem.Phys.80,2578 (1984).

10.1063/1674-0068/28/cjcp1410186to transfer the population from|v=16〉to|v=0〉.In a conventional control scheme for the achievement of population transfer,an intermediate state is considered to connect the initial and the target states.If the intermediate state is energetically located between initial and target states,it is named as a“Σ”-type control scheme, while if the intermediate state is located above the two states,it is named as a“Λ”scheme.Here,we consider connecting two“Σ”-type schemes together,which is named as a“double-Σ-type”scheme,to transfer population from the initial|v=16〉to the target|v=0〉.This is because the energy gap between the two states is too large and it is inefcient to transfer population via a single“Σ”scheme.As shown in Fig.1,the scheme consists of two steps∶The frst step is to transfer the population from|v=16〉to|v=7〉via an intermediate level|v=11〉, and the second one is to transfer the population from|v=7〉to|v=0〉via|v=3〉.

∗Author to whom correspondence should be addressed.E-mail：ychan@dlut.edu.cn

(Dated:Received on October 25,2014;Accepted on December 4,2014)