预应力锚索加固边坡的数值模拟分析

关志鹏，雷用，胡明

（1后勤工程学院军事土木工程系，重庆 401311；2重庆市城乡建设委员会，重庆 400014；3岩土力学与地质环境保护重庆市重点实验室，重庆 401311）

0 引言

预应力锚索是一种有效的边坡加固方法，在诸多工程实践中已经得到检验[1-5]。该方法适用于要求锚索承载力高、变形量小和需锚固于地层较深处的工程[6]。拉力型预应力锚索，主要是通过锚固段提供的握裹力和抗拔力达到加固边坡效果，锚索与水泥（砂）浆的粘结应力分布很不均匀的，锚固段与滑动带交汇处应力集中比较严重，随着荷载不断增大，在荷载传至锚固段最远端之前，锚索与注浆体界面或注浆体与地层界面就可能发生滑脱，这样就不能充分发挥锚索的加固效果。而压力型预应力锚索采用无粘结钢绞线，钢绞线与注浆体无粘结，注浆体与孔壁全长粘结。无粘结钢绞线孔底固定一个金属圆盘，作用在钢绞线上的拉力通过金属圆盘转换为压力，使注浆体受压，注浆体侧面与孔壁间产生剪应力[7]。

除了现场检测，数值方法是研究预应力锚索加固效果和稳定性评价有效的方法[8-12]。在ANSYS中对预应力锚索的分析方式主要有两种：一类是锚索和岩体的等效连续模拟，将锚索和岩体的作用一起考虑，用Link单元模拟预应力钢筋，采用降温法、初始应变法施加预应力；另一类是锚索和岩体的离散模拟，将锚索和岩体的作用分别考虑，以荷载的形式取代预应力钢筋的作用，用等效荷载法施加预应力[13～14]。这两种方法各有优缺点，总之，对于只是关注预应力锚索结构的基本性能时，可以考虑采用离散模拟方法，而对于研究预应力锚索结构局部的应力与应变响应时，宜采用等效连续模拟方法[14]。

本文主要采用ANSYS数值模拟对板肋式全粘结和自由段非粘结预应力锚索进行数值分析和稳定性计算，以此研究预应力锚索加固边坡效果，并对其进行稳定性评价。

1 工程概况

重庆某项目场地西南侧外围与市政道路之间的边坡需要进行治理，边坡长度约360m，高度10～25m，面积约6000m2，图1为部分现场图。 该场地属浅丘地貌，地势南东高北西低，由斜坡组成，场地高差49m。斜坡坡度角一般5 °～17 °。场地裂隙不发育，裂隙面结合程度差，岩层层面较平直，有泥质岩屑充填，局部呈张开状，宽1～2mm，结合程度差，属硬性结构面。

图1 工程现场部分图片

场区地层主要有第四系全新统人工填土（Qm41）、下伏侏罗系中统沙溪庙组的砂岩、泥岩（J2S）组成。经现场调查，场区内未见滑坡、危岩、崩塌、泥石流等不良地质作用，无地下洞室，未发现地质灾害，无地表水，水文条件简单，场地总体上稳定性良好。

由于施工后，预应力锚索的自由段由非粘结型施工（压力型锚索）变为水泥砂浆填充的粘结型，即锚索施工为全长粘结型锚索，与设计不符。因此，该边坡治理工程的质量及安全性存在隐患的可能，为保证该工程的安全使用，本文采用ANSYS数值模拟对其安全性进行分析与评价。

2 计算模型的建立

2.1 二维有限元计算

为了全面了解板肋式全粘结和自由段非粘结预应力锚索加固边坡效果以及对边坡稳定性进行分析，同时兼顾计算的可行性，选取一代表性剖面进行分析，如图2所示，边坡存在一外倾破裂面，有限元计算中，边坡破裂面采用一个单元网格厚度模拟。计算采用美国大型有限元计算软件ANSYS进行，计算按照平面应变问题处理。 岩体、砂浆、C30混凝土和C20混凝土用平面实体单元六节点的三角形单元PLANE82模拟，预应力锚索采用杆单元LINK180模拟，截面尺寸在实常数中输入，所有单元需要事先画好。有限元网格划分如图3所示。

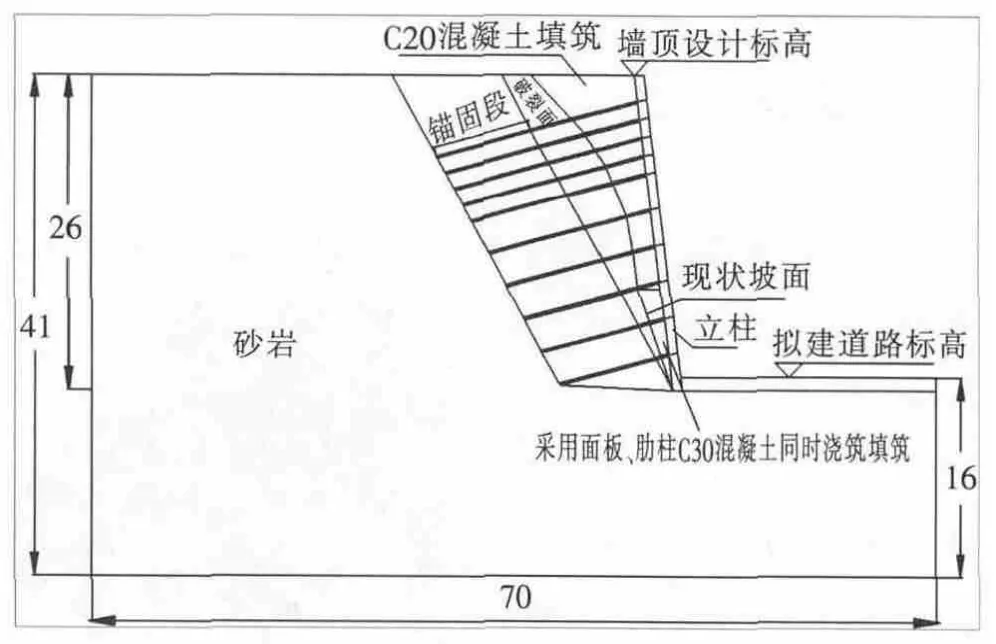
图2 计算剖面

图3 有限元网格

建立模型时，在原设计的基础上增加两排预应力锚索进行计算。本次有限元模拟的工况包括：（1）全粘结拉力型预应力锚索；（2）自由段非粘结拉力型预应力锚索；（3）压力型预应力锚索。

ANSYS软件提供单元“杀死”功能，自由段非粘结采用这种方法实现。

边界条件：底部固定，左、右两侧水平约束，重力荷载通过设置重力加速度的方式模拟，边坡上部施加130kN/m荷载。

拉力型预应力锚索采用降温法施加预应力，预应力锚索所需降低的温度通过下式计算：

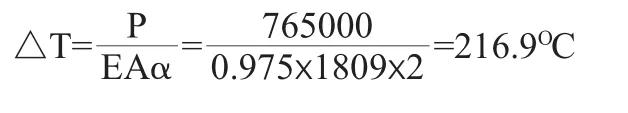
式中：P—预应力

E—弹性模量

A—截面积

α—线膨胀系数，2×10-5

压力型预应力锚索采用在注浆体锚头和锚固段底部施加集中力的方法施加预应力，施加的集中力即锚索的锁定荷载F=765kN。

有限元计算输入的材料参数值如表1所示。

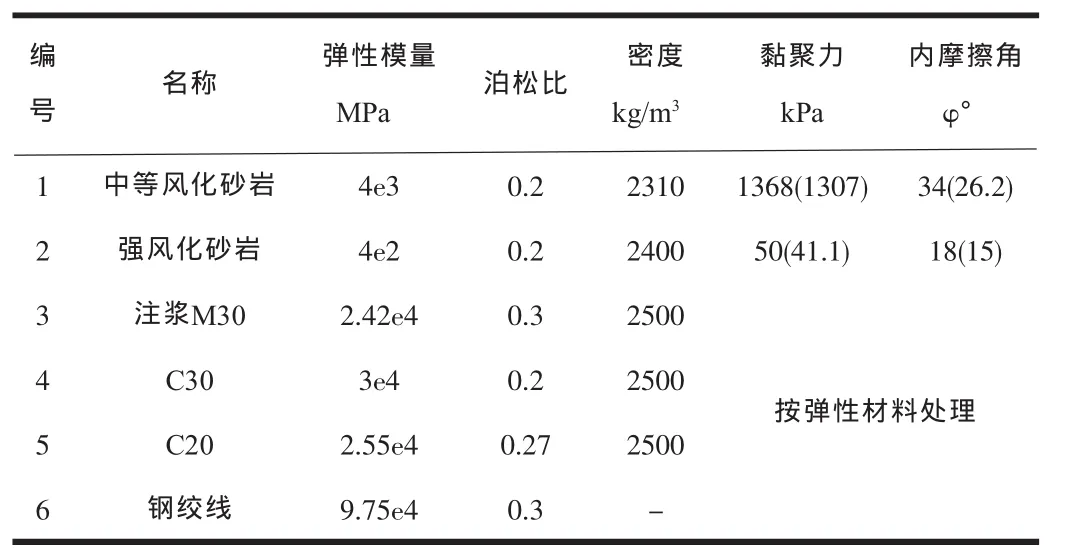
表1 有限元中输入的材料参数表

2.2 三维有限元计算

选取代表性剖面所在的两伸缩缝之间的边坡建立三维有限元模型，为了简化计算，利用代表性剖面拉伸成三维模型进行计算，模型建立范围为沿边坡方向拉伸18m。岩体用三维实体单元SOLID45模拟，锚索用杆单元LINK180模拟。 考虑到计算时间问题，将锚索孔进行简化，仅用锚索单元模拟预应力锚索，因此三维模拟仅能用于计算全粘结拉力型预应力锚索，同样采用降温法施加预应力。所有单元需要事先画好，单元总数达315600个。有限元网格划分如图4所示。

边界条件：模型底部固定，四周水平方向约束，重力荷载通过设置重力加速度的方式模拟，边坡上部施加130kN/m荷载。

材料参数见表1。

图4 三维有限元网格

3 计算结果分析

3.1 加固效果分析

分别对3.1和3.2中的有限元模拟工况进行数值模拟计算，计算结果见表2。

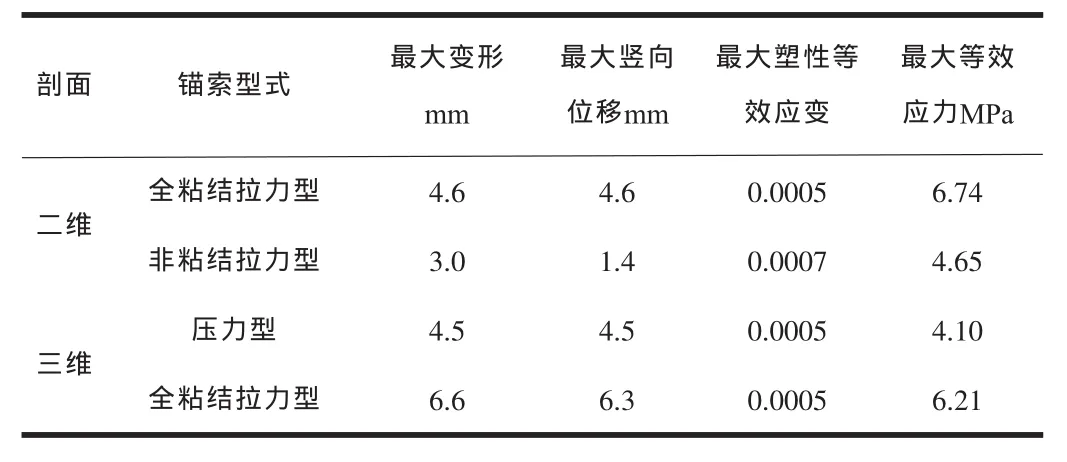
表2 有限元分析结果

由表2可知，全粘结预应力锚索的最大变形、最大竖向位移和最大等效应力均大于自由段非粘结预应力锚索和压力型预应力锚索，但数值均较小。最大塑性等效应变值较小，说明边坡的塑性区很小，预应力锚索的加固效果较好。

最大等效应力主要发生在破裂面与锚索交汇处，由上表可知压力型锚索最大等效应力小于全粘结和自由段非粘结拉力型锚索，非粘结拉力型和压力型预应力锚索的最大等效应力相差较小，因此对于全粘结拉力型预应力锚索，在滑带处产生应力集中。

表3 原设计有限元应力分析结果

表3为原设计，即没有增加两排锚索时自由段非粘结和全粘结预应力锚索应力值，应力集中主要发生在破裂面与锚索交汇处，因此表中的应力反映的是此交会处的应力集中情况。自由段非粘结和全粘结都有一定的应力集中情况，但全粘结的应力集中比较明显，应力值较大。

3.2 稳定性评价

本次评价主要通过有限元强度折减法计算边坡破坏时的折减系数，即为边坡的安全系数。有限元强度折减法原理为[15]：

对于岩土中广泛采用的莫尔一库仑材料，强度折减安全系数w可表示为

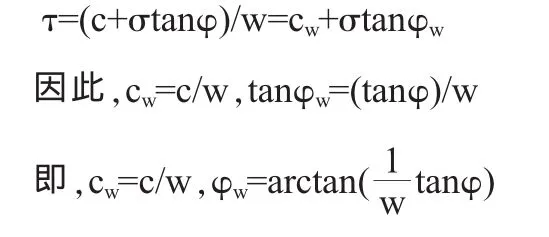
cw、φw为折减后得到的黏聚力和内摩擦角，w为折减系数，有限元计算中不断降低边坡中岩土抗剪强度直至达到破坏状态为止。程序根据有限元计算结果自动得到破坏滑动面，并获得安全系数。

有限元强度折减法的优点主要是[16]：考虑了土体的非线性弹塑性本构关系；能够动态模拟边坡的失稳过程及其滑移面形状；在求解安全系数时，不需要假定滑移面的形状，不需要假定土条之间的相互作用力。

通过增大折减系数，减小黏聚力和内摩擦角使边坡计算不收敛，最终得到边坡的稳定安全系数，计算参数见表4。

图5和图6为二维计算加固前后塑性等效应变图，图7和图8为三维计算加固前后塑性等效应变图。从图中可以看出，对于二维计算，加固前，当折减系数w=1.1时边坡的塑性区基本已经贯通，塑性应变值为0.02，继续增大折减系数后，计算将不收敛，因此边坡加固前的稳定系数为w=1.1；加固后，当折减系数w=2.8时边坡的塑性区基本已经贯通，塑性应变值为0.0025，继续增大折减系数后，计算将不收敛，因此取w=2.8为二维计算的安全稳定系数。对于三维计算，加固前，当折减系数w=1.2时边坡的塑性区基本已经贯通，塑性应变值为0.0004，继续增大折减系数后，计算将不收敛，因此边坡加固前的稳定系数为w=1.2；加固后，折减系数w=3.0时边坡塑性区基本贯通，塑性应变值为0.0026，因此取w=3.0为三维计算的安全稳定系数。

表4 折减计算参数

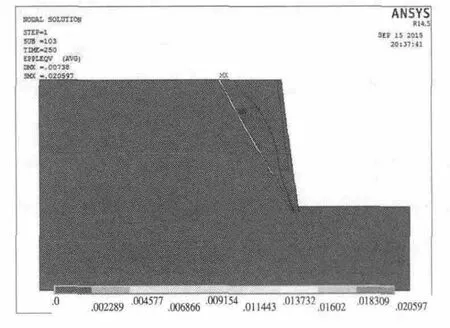
图5 二维计算加固前塑性等效应变图（w=1.1）

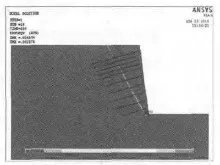
图6 二维计算加固后塑性等效应变图（w=2.8）

图7 三维计算加固前塑性等效应变图（w=1.2）

图8 三维计算加固后塑性等效应变图（w=3.0）

综上，预应力锚索加固前，边坡的稳定系数为w=1.1，处于相对不稳定状态，需要加固；预应力锚索加固边坡后，有限元计算得到的稳定安全系数可取w=2.8，达到了加固边坡的效果。

6 结论

拉力型和压力型预应力锚索在加固机理和加固效果上都有所不同，在边坡加固设计、施工时要充分了解其特点才能达到理想的加固效果。数值计算是研究预应力锚索较为有效实用的一种分析方法，本文采用ANSYS软件对某一工程进行分析，主要得到以下结论：

（1）预应力锚索加固边坡后，边坡的最大变形、最大竖向位移、最大塑性等效应变和最大等效应力均较小，边坡塑性区很小，此外，有限元计算得到的稳定安全系数为w=2.8，达到了加固边坡的效果。

（2）从受力角度分析，最大等效应力主要发生在破裂面与锚索交汇处，压力型锚索最大等效应力小于全粘结和自由段非粘结拉力型锚索，因此对于全粘结拉力型预应力锚索，在滑带处产生应力集中，从这个角度看，压力型预应力锚索具有优越性。

（3）通过等效应力分析，未增加两排锚索时，自由段非粘结锚索和全粘结锚索都有一定的应力集中情况，但全粘结的应力集中比较明显，应力值较大。

[1]Brahim Benmokrane，Gerard Ballivy.Five-year monitoring of load losses on pre-stressed cement-grouted rock anchors[J].Can Geotech J，1991（28）:668-677.

[2]李小青，徐俊，张伟，等.预应力锚索在滑坡体治理中的应用研究[J].华中科技大学学报，2004，21（4）:20-22.

[3]雷金山，杨秀竹，王安正，等.压力型锚索锚固工程原型监测与分析[J].铁道科学与工程学报，2011，8（6）:64-69.

[4]吴润泽，周海清，胡源，等.基于有限差分原理的预应力锚 索 抗 滑 桩 改 进 计 算 方 法 [J].岩 土 力 学 ，2015，35（6）:1791-1800.

[5]王水生.高危岩质边坡综合支护设计研究[J].山西建筑，2015，41:80-82.

[6]CECS 22:2005，岩土锚杆（索）技术规程[S].

[7]孙凯，孙玥.拉力型和压力型预应力锚索受力分析及工程应用[J].预应力技术，2007（3）:25-29.

[8]李英勇，张顶立，王松根.预应力锚索锚固作用机理的数值模拟研究[J].岩土力学，2006，27（S2）:921-925.

[9]夏元友，范卫琴，芮瑞，等.压力分散型锚索作用效果的数值模拟分析[J].岩土力学，2008，29（11）:3144-3148.

[10]熊保林，王希良，路春娇.高边坡预应力锚索格子梁加固系统三维有限元分析[J].铁道建筑，2010（2）:67-70.

[11]戴自航，石金华，卢才金.预应力锚索框架梁加固滑坡的稳定性数值分析[J].铁道科学与工程学报，2014，（3）:9-16.

[12]黄志全，张瑞旗，王安明.基于FLAC 3D的桩锚支护结构变形分析[J].水利与建筑工程学报，2015，（2）:68-72.

[13]何本国.ANSYS土木工程应用实例[M].北京:中国水利水电出版社，2011.

[14]李宁，张鹏，于冲.边坡预应力锚索加固的数值模拟方法研究[J].岩石力学与工程学报，2007，26（2）:254-260.

[15]郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学，2002，4（10）:57-62.

[16]胡明，雷用，赵晓柯.基于ANSYS的倾斜微型桩支护边坡稳定分析 [J].地下空间与工程学报，2014，10（增1）:1689-1693.