一类单位圆上单叶正则函数的分类
2015-01-12李小光
李小光
(西安航空学院理学院,陕西西安710077)
一类单位圆上单叶正则函数的分类
李小光
(西安航空学院理学院,陕西西安710077)
为研究单位圆上单叶正则函数的性质。运用单叶解析法得到零点处函数值等于零、导数值等于1的函数具有的一些重要性质,给出这些性质的分类,分别是:幂级数展式的系数估计、模的估计、像区域范围的估计。单叶正则函数的性质及其分类是研究复变函数几何理论的基础,对复变函数基础性研究具有一定的现实意义。
单叶解析;系数估计;模的估计;像区域范围的估计
定义1令n=l,2,…,对于k=l,2,…,n称
为de Branges函数[1]。其中(a)v是a(a+l)…(a+v-l)的缩写。如果令τk+l(t)=O,则有
定理1(面积定理)[2]设函数在区域l<上单叶解析,在z=∞有一次极点,则

1、系数的估计







适合f(D)J的函数f在S中就D内局部一致收敛来说是稠密的,因此仅需对这些函数证明式(9)。

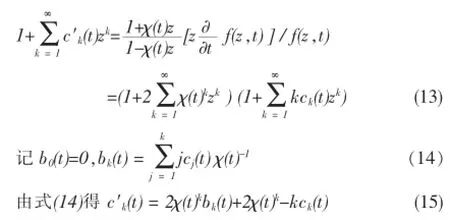
令n=l,2,…固定,考虑

其中τk(t)是de Branges函数。
下面我们省略变量t,由式(14)得


2、模的估计[6-8]



由式(17)—(18),可得到下列定理


证明设z=reiθ是单位圆内的点,在式(17)两边积分

同理在式(18)两边从O到r积分得

沿着直线从O到z对式(11)的右边积分


综合以上积分得到

3、像区域范围的估计[9]
定理7(面积掩蔽定理)[10]设函数在内单叶解析,则由w=f(z)把变换为W平面上的一个区域B,则此区域B必含有圆,而未必含有半径更大的同心圆。
推论1[11]如果f(z)在上单叶解析,f(O)=O,在圆上不取数值c,则f′(O)≤4c。
[1]Imai Y,Iseki K.On axiom systems of propositional calculi xiv[J].Proc.Japan A cademy,1966,42:19-22.
[2]Borzooei R A,HasanKhani A,Zahedi M M.On hyper k-algebras[J].Mathematicae Japonicae,2000,52(1): 113-121.
[3]Borzooei R A,Harizavi H.Regular Congruence relations on hyper Bck-algebras[J].Scientiae Mathematicae Japonicae,2005,61(1):83-97.
[4]Bakhshi M,Borzooei R A.Lattice structures on fuzzy congruence relations of a hypergrouoid [J].Information Science,2007,177(16):3305-3313.
[5]Borzooei R A,Zahedi M M.(Anti)fuzzy positive implicative hyper k-ideals[J].Italian J.Pure and Appl.Math,2003,14:9-22.
[6]王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2000.
[7]吴忘名.Fuzzy蕴含代数[J].模糊系统与数学,1990,4(1):56-63.
[8]谢云鹏.基于包含度的模糊不定性度量[D].西北大学, 2008:18-28.
[9]姚炳学.群和环上的模糊理论[M].北京:科学出版社, 2007:84-88.
[10]戈鲁辛.复变函数的几何理论[M].科学出版社,956.
[11]钟玉泉.复变函数[M].高等教育出版社,2003.
O175.14
A
1674-6198(2015)05-0054-03
2015-07-11
陕西省科技厅自然科学基础研究基金资助项目(2013JM 1019);西安航空学院校级科研立项(13XP13)
李小光(1973-),女,辽宁铁岭人,西安航空学院副教授,从事代数学及信息论方面的研究。
