摩尔库伦准则下层状围岩隧道支护应力的上限解
2015-01-11姚广
姚 广
(湖南科技大学,湖南 长沙 411201)
0 引言
我国大约2/3国土面积是山地和丘陵,在交通基础设施建设的过程中不可避免要修筑大量隧道。我国隧道修筑起步较晚,与发达国家相比,我国的隧道修筑技术还存在一定的差距。伴随着交通基础设施的发展,层状围岩隧道在交通建设过程中越来越频繁地出现,同时,层状围岩隧道的建设难题对我国工程科研人员提出了新的技术挑战。近年来,国内学者对层状围岩隧道做了大量的研究,并获得了较多科研成果。王祥秋(2002)[1]进行了含软弱夹层层状围岩的非线性有限元分析;任海军(2007)[2]基于层状围岩的破坏条件和块体失稳原理,对隧道开挖过程中层状围岩稳定性进行了综合性评价,探讨了层状围岩隧道塌方的原因;钟放平(2008)[3]提出了层状围岩中隧道开挖支护的优化措施,利用现场试验和数值模拟的方法,分析了喷锚支护参数优化后锚杆受力和围岩变化特征;杨峰(2008)[4]研究了连拱隧道层状围岩支护结构的变形受力特点;冯文凯(2009)[5]根据现场试验提出了高速公路隧道层状围岩支护优化措施;马永政(2009)[6]在DDA法和无网格法耦合的条件下研究了隧道层状围岩的变形;李晓红(2010)[7]利用现场监测和数值模拟的方法,研究了层状围岩中深埋隧道变形破坏特征;闫永杰(2011)[8]研究了隧道顶板变形特征,分析了层状围岩在隧道开挖过程中离层机理。
本文基于摩尔库伦准则,利用极限分析上限定理构建隧道支护反力塌落模型和机动速度场,推导支护结构内部能量耗散与外部功率方程,得出层状围岩隧道支护反力的上限解。
1 层状岩体隧道支护应力的上限解
1.1 上限解的求解
在摩尔库伦准则下采用极限分析上限法求解层状岩体圆形隧道围岩支护应力最小上限解,由于极限分析上限法并不需要考虑层理面对围岩支护应力的影响,所以只考虑了不同层状岩体在重力场作用下对围岩支护应力的影响,即只考虑不同层状岩体的黏聚力和内摩擦角等影响因素。公式推导过程中假设岩体材料为完全塑性。
采用图1所示的层状岩体破坏模式,图中D为隧道洞径,H为隧道埋深,其中第i层岩体的厚度为Hi,容重 γi,剪切强度 Cui,内摩擦角度 φi,隧道两侧滑移角 2θ。

图1 层状岩体隧道的塌落模型
由图1可知,计算模型由层状岩体(1、2…n)、块体(1、2)组成,各岩体、块体的速度场、外力分布如图2、图3所示。

图2 速度场图示
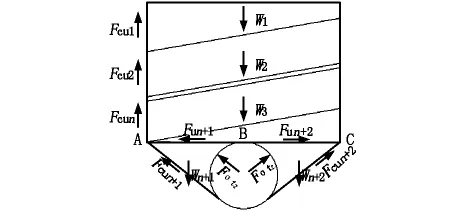
图3 外力分布图示
图2中滑移面AB、BC长度分别用X和Y表示,则:
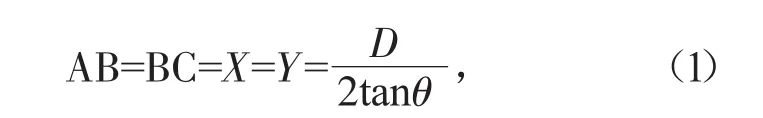
在图2中,UAB和UBC表示滑移面AB与BC的速度;U1、U2…Un分别表示层状岩体 1、2…n 的速度;Un+1、Un+2分别表示块体1、2的速度;各速度之间的表达式如式(2):
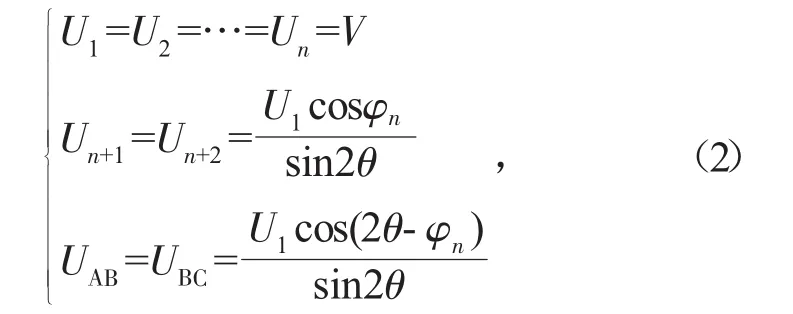
图3中W1、W2…Wn分别表示各层岩体的重力;Wn+1、Wn+2表示块体 1、2 的重力;Fcu1、Fcu2…Fcun、Fcun+1、Fcun+2表示各接触面上的剪切力;各层岩体块体重力与接触面剪切力表达式如式(3):

图3中隧道的支护反力可表示为:
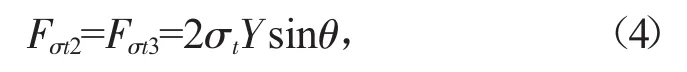
根据极限分析上限定理,外力功率应等于内部能量耗散功率,即:

式中:Pw,为外力功率;Pσt是支护反应力作用下的能量耗散功率;Pv是速度场作用下的能量耗散功率。
各部分功率表达式如式(6)所示:
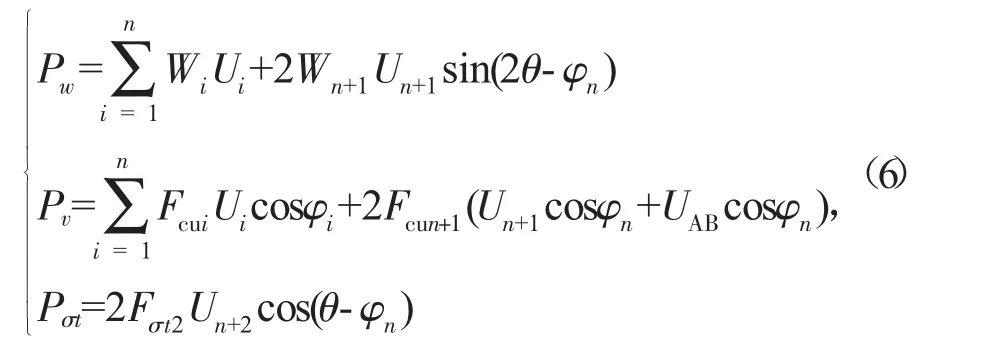
联立式(5)、式(6)可得围岩支护反力的最小值,即围岩最小支护反力的上限解,其表达式如式(7):
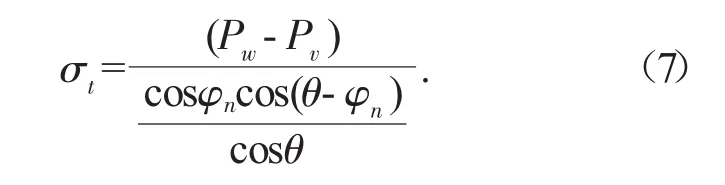
1.2 成果验证
为了验证本文成果的准确性,引入临界稳定率[9]的概念。采用文献[9]中的算例,通过本文推导出的公式(7)求算出支护反力,进而求算出临界稳定率并与文献[9]中的临界稳定率进行比较,验证公式(7)求算出的支护反力是否准确。
临界稳定率表达式为:

式中:σs为地表作用均布荷载,无地表荷载时取零。
计算过程中采用几何参数及土体强度参数如表1 所示[9]。

表1 隧道几何参数及层状围岩参数
采用MATLAB计算软件,使用表1中隧道的几何参数及层状围岩强度参数,运用公式(7)计算围岩支护反力,具体计算结果如图4所示。

图4 层状岩体隧道支护应力计算结果
将图4中的支护反力代入公式(8)求算出临界稳定率N,具体计算结果如表2。

表2 隧道稳定率最小上限值
通过本文推导出的公式(7)求算出支护反力,进而求算出临界稳定率并与E.H.Davis[9]的结果进行比较,可知两者极为接近,进而证明了本文支护反力的计算结果是可靠的,公式(7)可以作为层状围岩支护反力的上限解。
2 结论
本文根据极限分析上限原理得出了层状围岩隧道支护应力,并通过算例进行了验证。该上限解的得出对层状围岩隧道的支护参数选取有着积极的指导意义。
