有限元极限分析法在岩土工程中的应用

陈管仲

（重庆市蜀通岩土工程有限公司 重庆 401147）

有限元极限分析法在岩土工程中的应用

陈管仲

（重庆市蜀通岩土工程有限公司 重庆 401147）

对于有限元极限分析法来说，它优越于经典极限与数据等传统的分析的方法，是一种新型的岩土工程的分析方法，被广泛的应用于对岩土工程的设计分析阶段。有限元极限分析法能够有效地应用于一些非均匀的、强度不均匀的岩土工程的分析，有限元极限分析法通过荷载增加与强度降低等方式，能够直接计算出岩土的滑动面与安全系数，能够很好的满足岩土工程设计与分析的要求。本文将对有限元极限分析理论进行相应的介绍，就连续性问题的离散相关情况进行必要的分析与计算，并对有限元极限分析法在对滑坡的岩体分析中的应用进行相应的介绍，希望通过本文的相关介绍，对相关工作者有所帮助。

有限元极限分析法；岩土工程；应用

1 引言

20世纪，我国在岩土工程的研究方面，就开始引进了外国的有限元极限分析法，经过多年的使用与发展，为了提高计算的精度以及应用的范围等，对有限元极限分析法展开了相应的研究，并做出了相应的改进。对于有限元极限分析法来说，它比传统的岩土分析方法都要优越，且能够很好的满足岩土工程设计与分析的需要，能够有效地提高岩土工程的设计质量。本文将通过对有限元极限分析法相关理论进行必要的介绍，并就有限元极限分析法的应用进行相应的介绍。希望为岩土工程建设工作者提供参考。

2 有限元极限分析法基本原理

对于极限分析法的力学来说，要求岩体必须处于刚塑性状态并具有良好的弹塑性，要求岩土处于一个极限的平衡状态，也就是说，滑动面上的作用力与抗剪力相等或者体滑动面上每点的剪应力与土体的抗剪强度相等，这是现实中并不存在的现象。当岩土处于极限平衡状态时，土体已经处在濒临破坏失稳的状态，这时岩土的材料强度得到充分发挥，这也是判断岩土是否已经失稳的重要依据。通常我们把岩土的极限平衡状态作为我对岩土工程设计的主要依据，它是保证岩土工程安全可靠的基础。

2.1 安全系数

通过使用有限元极限分析法能够有效地且准确的对岩土的安全系数进行定义，同时还可以根据岩土工程的破坏程度进行及时的调整。这样能够很好地满足对岩土工程相关计算与分析。

对于滑坡工程来说，环境因素将对岩土工程的质量造成重大的影响，当岩土工程的强度下降时，容易造成滑坡的稳定性被破坏。在这些工程中，可以使用相应的强度贮备系数来对岩土工程的强度进行计算，同样也可以通过把岩土的强度降低，来对岩土进行破坏，以完成相应的有限元的相关分析与计算。

对进行有限元的分析与计算过程中，我们把强度下降的倍数作为岩土工程的强度贮备系数。由于有限元极限分析法具有这种特征，又可以根据这一特性把有限元极限分析法叫做强度折减分析法。采用有限元分析法对岩土的安全系数进行相应的计算，主要就是计算岩土的强度贮备系数。如：在对地基的岩土安全系数进行计算的时候，往往地基的所要承受的荷载比较大，这使得地基的压力太大，导致地基出现失稳现象，这种情况下，我们又把荷载增大倍数作为超载安全系数，同时也将成为增量加载数值。通过这种方法计算得到的安全系数都是超载系数，通过使用不同的定义来对安全系数进行定义计算的结果有着极大的差别，即便使用同一种定义方法来计算推力，也会有着一定的差别。

2.2 有限元分析原理

对于有限元分析法来说，它主要使用了莫尔-库仑的计算方法，其计算公式如下：

在使用有限元分析法来对滑坡岩土进行相关的分析计算时，要不停地减小滑坡岩土抗剪强度，直到滑坡的岩土结构发生破坏为止，同时通过破坏的时间来获得强度贮备系数。对于正常的岩土来说，它具有两种强度，分别为计算公式中的c与tanφ，对于这两个指标来说，要使用统一的强度贮备系数，所以当这些指标下降时，这两个指标必须维持相同的比例下降，然而在实际当中，岩土是不可能呈现出这种下降趋势的同时这也是当前强度贮备系数所存在的一个不足之处。

在对岩土进行施工过程中，对岩土的破坏表现出逐进式的破坏方式，然而对于岩土体来说，它将从线弹性慢慢变为塑性流动。最终使得岩土体所承受的压力的能力到达极限，发生破坏。对于增量加载的情况正是求出地基极限承载力的重要方法，在荷载不断增加的过程中，岩土体逐渐从原来的弹性变形变为塑性变形，最后转变成极限的破坏形式，在相应的过程中增加相应的荷载，也就是需要计算的极限荷载。使用这种方法，可以计算出相应的岩土工程的极限荷载，这种方法所得到的结果比较准确，通常我们又把这种方法称为有限元超载法。

2.3 有限元分析法的优势

对于有限元分析法来说，它具有极大的优势，包含了传统的经典分析以及继承数值分析所有的优点，能够很好的发挥出数值分析的高度适应性，同时也表现出在岩土工程的设计过程中经典分析的实用性，能够很好的满足岩土工程中的相关应用。

采用有限元分析法对岩土工程进行分析计算时，并不需要对滑移面的形状以及位置进行确定，能够较为准确的且直接计算出边坡的安全系数，进行的相关计算并不需要相应的条分，能够直接根据程序计算出滑面的系数与强度贮备系数。在采用有限元分析法对地基的承载力进行计算时，可以使用超载法对地基的承载力进行计算，并不需要对破坏的位置进行假设，也不需要进行相关的理论解答，通过相应的程序便可以对相关的数据进行处理，同时还能够直接给出对应的滑面极限承载力。所以有限元分析法能够满足多种复杂的岩土工程当中，而且不会应用岩土的材料性质以及几何形状等问题而受到限制。

3 连续问题离散

可以采用三节点三角形对连续问题离散进行必要的分析与研究，通过相关的分析与研究可以看出，每个单元之间会有一个不连续的应力面，如图1表示不连续的应力面情况。对于该节点来说，它的优点是该节点的相应的变量满足屈服准则，每个单元的内部能够直接根据屈服准则进行相应的计算，能够有效的加强应力面的自由度，能够有效地解决图1当中的应力面情况插值缺陷。

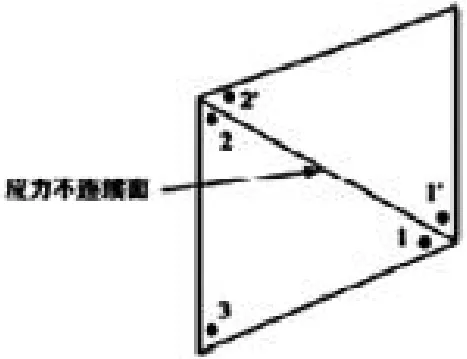
图1 不连续的应力面情况

为了让相关的计算更加方便，可以使用下面的相应的符合对其辅助标记：Th表示三角剖分，其中存在E单元，可以用Ωe来表示。对于单元相应的边界来说，可以用对应的αΩe来表示，对于其边界来说，由3个部分组成，即不连续的面、速度边界以及应力边界，在对单元内的应力进行计算时，可以使用下面的公式进行计算：

4 有限元极限分析法的应用

可以通过有限元极限分析法来对滑坡强度折减数据进行相应的分析与计算。在进行相关的计算之前，我们先做出相应的假设，即假设有一均质滑坡，该滑坡的高度为20m，岩土的粘聚力为41kPa，土容重γ为22kNPm3，内角度为18°，先我要对其使用有限元极限分析法来对滑坡强度折减相关的数据进行必要的计算，当β角度分别为30°、35°、40°、45°、50°时，滑坡的滑动面以及边坡安全系数。

我们可以使用ANSYS5.72版本的软件来进行相应的有限元的分析与计算，在进行计算之前，要根据实际需要与要求制作相应的有限元模型，边界条件使用两侧水平约束的方法，并且假设模型的下部是固定的，并且上部是完全自由的，如图2所示。

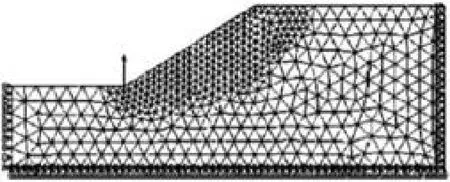
图2 有限元模型

通过与传统的经典分析以及继承数值分析法进行比较可以看出，采用有限元极限分析法对岩土工程进行的计算更加准确，且在计算效率方面有着很大的提升，特别是在对强度折减系数进行的计算，准确率得到大大的提升。在对平面应变进行的相关计算时，可以使用莫尔-库仑屈服准则进行相关的计算，同时还可以与非关联流动法则进行配合，能够有效地提高计算的准确率。通过相关的计算比较可知：采用有限元极限分析法对岩土工程进行的计算结果与传统方法的计算结果的误差仅为5%，在准确率上面超过了传统分析方法的30%左右。

5 结束语

通过本文的介绍可知：通过有限元极限分析法对岩土工程进行的计算，要优于传统的经典分析以及继承数值分析法，并不需要做出相应的破坏假设。通过使用网格适应模式能够自动的对岩土结构的破坏形式进行计算，能够有效的提高岩土工程的相关计算的精度，为建筑的施工建设提供了可靠的依据。希望通过本文关于有限元极限分析法在岩土工程中的应用相关的介绍，对读者有所帮助。

[1]郑颖人，赵尚毅，邓楚键，刘明维，唐晓松，张黎明.有限元极限分析法发展及其在岩土工程中的应用[J].中国工程科学，2006：50～52.

[2]李大钟，郑榕明，王金安，杨毅，李娜.自适应有限元极限分析及岩土工程中的应用[J].岩土工程学报，2013：87～96.

[3]郑颖人.岩土材料的破坏与极限分析方法的发展[A].塑性力学新进展——2011年全国塑性力学会议论文集[C].2011：56～57.

TU43

A

1673-0038（2015）24-0272-02

2015-5-24

陈管仲（1980-），男，工程师，本科，主要从事地质勘察方面的工作。