泵头体材料的声发射信号特征

2015-01-10顾桂华修吉平

无损检测 2015年4期

顾桂华，修吉平，刘琼，张伦

（1.华中科技大学材料科学与工程学院，武汉 430074；2.江汉石油第四机械厂，荆州 434000）

压裂作业主要通过压裂机组泥沙和水混合后进行加压，通过高压管道注入井底，人为地改变油气层的物理结构，降低地层阻力，提高油气井的产量［1］。压裂作业的核心部件是泵头体，由于承受高压循环载荷作用和工作介质的侵蚀，大型压裂机组所使用泵头体容易出现早期失效［2］。而直接用泵来做试验测试十分昂贵，利用超高压模拟试验平台，将不同材料加工成统一规格的试块，结合声发射检测系统，得出不同泵头体材料试块的失效时间，为材料的选型提供试验依据。

1 试验设备

超高压试验模拟平台由柱塞泵、进出管路、变频器、电机等组成。柱塞泵选用JN280系列柱塞泵中的一款，其最高能产生280 MPa的压力，理论流量30L／min，柱塞直径20mm，泵速390次／min，配备110kW 电机，工作转矩705N·m。泵的液力端压力输出值由变频器驱动控制。

声发射检测系统采用VB6.0和Matlab为开发平台，选用凌华PCI9812 高速采集卡，单通道采样速度设定为3 M／s，具有12位A／D 分辨精度，A／D量程在－5～5V 之间。声发射传感器选用北京声华公司的SR－150M 声发射传感器。整个系统框图如图1所示。

2 试验方法

2.1 试验原理

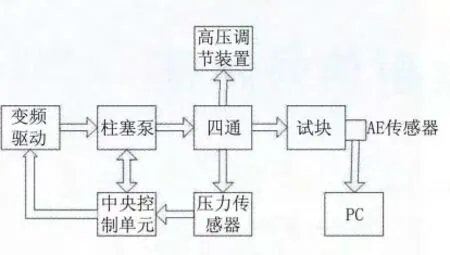
图1 系统框图

声发射（Acoustic Emission，简称AE）作为无损检测的一种技术手段，在材料内部产生缺陷与损伤时，利用高灵敏度的传感器，接收来自这些缺陷或损伤产生的应力波，即AE 信号［3］。通过分析这些信号，来评估材料的缺陷或损伤特征。金属材料中的位错运动、滑移带生成、晶界滑移、裂纹萌生与扩展等均会有相应的AE 信号，可以很好地检测到材料何时出现损伤或缺陷，对试件的结构完整性作出评价［4］。而且声发射传感器的安装比较方便，能在许多复杂的条件下应用。

2.2 试块结构

由于实际泵头体造价昂贵，不宜用来做试验，为此，笔者搭建了高压模拟平台模拟泵头体实际工作时的工况，而将泵头体材料加工成相对简单的试块来进行试验，利用声发射技术分析整个试验过程中试块状态的变化，即裂纹的产生、扩展的规律。试验最根本的目的是得到在特定工况下材料的寿命，如果寿命越长，说明材料越适宜做泵头体材料。图2（a）是实际泵头体，在服役一段时间后就发现漏水，内部产生裂纹，如图2（b）所示，有一条明显的肉眼可见的裂纹。

图2 3000型五缸泵头体及其裂纹宏观形貌

试块由一个长170mm，宽170mm，厚75mm 的毛坯加工而成。将试块中央内腔加工成圆柱楔形，并在楔形尖部采用圆角，确保了破坏性试验的可行性，形成了可预见性的裂纹，也便于确定安装声发射传感器的位置。在对试块内腔加压的过程中，沿楔形圆角轴向方向距底面最近的线上应力集中度最大，裂纹极有可能在该线附近产生，并沿着线延伸直至试块破裂。试块中央腔体的密封采用高强度焊接，并将垫板和焊接面外侧用大螺栓紧紧固定在一起。4个φ33 mm 的通孔为螺栓孔，用于将试块和垫板固定在一起，最终装夹到超高压试验平台上，如图3所示。

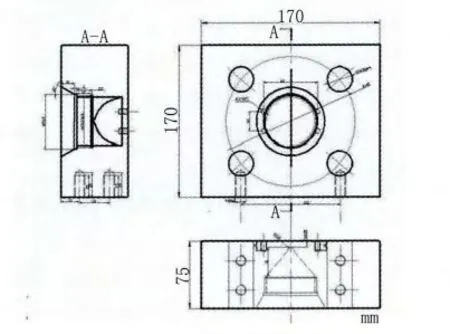
图3 试块结构示意

模型的设计有两个关键值：一是圆角处的最大应力值（简称最大应力），此值对应泵头体破裂处应力；二是圆角对应底面的应力值（简称表面应力），此值对应漏水螺纹孔处的应力。设计试块结构时，要尽可能使泵头体和试块两者的最大应力和表面应力接近，模拟泵头体材料的实际使用寿命。在整体及螺纹孔位置尺寸不变的情况下，有3个参数影响这两个关键值，包括圆柱楔形开口直径、底面厚度（或楔形深度）和楔形顶部圆角半径。为保持与实际泵头体模拟时相同，对这3 个变量进行ANSYS模拟选出最佳参数：开口直径为4 mm，底面厚度为7mm，圆角半径为2.8mm。此时应力集中处的最大应力为836MPa，表面应力为226 MPa，与实际泵头体模拟出的数据较为接近，以此作为试块模型的设计参考数据［5］。表1 详细列出了泵头体实际工况与模拟平台系统的对比解决方案。

2.3 试验材料

试验材料是经调质处理的Cr－Ni－Mo－V 低合金超高强钢，高强度钢的主要力学性能为：硬度为33～38 HRC，抗拉强度为1 280 MPa。由于Cr、Ni、Mo等元素的存在，尤其是Ni元素的大量存在提高了钢的强度和低温冲击韧性［6］。

表1 实际工况与模拟环境相似性对比及解决方案

2.4 试验方法

将试块装到超高压模拟试验平台上，在声发射传感器与试块表面涂上超声波耦合剂，安装好声发射传感器。启动超高压试验模拟平台，设定目标压力150 MPa，保护压力180 MPa。压力波形图如图4所示，图中峰值压力已经达到了150 MPa。这样的压力循环特征跟实际泵头体承受的载荷特征基本一致，属于交变载荷，压力值从0上升到峰值后再下降到0，与实际工况十分吻合，保证试块内腔的载荷条件跟实际泵头体的载荷条件一致。

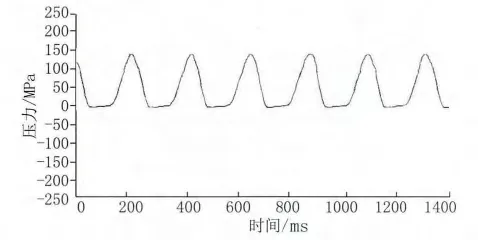
图4 高压模拟平台压力曲线

当超高压试验模拟平台压力显示值到达设定的150 MPa时，打开声发射检测系统，点击开始采集，记录全过程连续采集到的信号。试验进行到试块冲破喷水时，点击停止采集，同时也停止超高压试验模拟平台的运作。

2.5 现场噪声干扰

2.5.1 变频电机对整个电网的影响

现场高压泵柱塞运动的快慢由变频器的频率来设定，从而控制试块中央内腔承受的压力峰值大小。变频器一般由整流电路、滤波电路、逆变电路组成。由于变频器逆变电路的开关特性，电网中会存在能构成电源无功损耗的较低次谐波信号以及许多频率较高的谐波分量，形成对变频器本身以及其他设备，尤其是通讯设备的干扰信号。

对信号进行快速傅里叶变换，发现高次谐波的频率都在3kHz以下，并且在时域图上幅值很小，对于声发射信号检测的干扰不大。

2.5.2 机械装置产生的噪声

高压泵现场机械装置复杂，有前置低压泵、过滤器、各路管道等。当柱塞运动起来后，现场会产生机械振动以及噪声。经过采集这部分信号进行分析，高压泵机械装置的噪声频率大多在70kHz附近。而金属裂纹的频率大多在100kHz以上，所以在频谱图上可以区分出裂纹信号。

2.6 声发射信号处理

2.6.1 快速傅里叶变换FFT

FFT 是离散傅里叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上杂乱无章，难观察出其特征，但如果变换到频域后，就容易看出其特征，这是很多信号分析采用FFT 变换的原因。一个模拟信号，经过ADC 采样之后，就变成了数字信号。采样定理要求采样频率大于信号频率的两倍，采样得到的数字信号可以做FFT 变换。N个采样点经过FFT 之后，可得到N个点的FFT结果，为了方便进行FFT 运算，通常N取2的整数次幂。假设原始信号的峰值为A，那么FFT 结果的每个点（除了第一个点直流分量之外）的模值就是A的N／2倍。第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（假设的第N＋1 个点，也可看做是将第一个点分做两半，另一半移到最后）则表示采样频率Fs，这中间被N－1个点平均分成N等份，每个点的频率依次增加。例如某点n所表示的频率为：Fn＝（n－1）×Fs／N。

2.6.2 小波分析

小波变换对于分析瞬时突发信号非常有用，能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，解决了傅里叶变换不能解决的困难。小波变换的本质和傅里叶变换类似，也是用精心挑选的基函数来表示信号方程。每个小波变换都会有一个mother wavelet，称为母小波，同时还有一个scaling function，即尺度函数，也被称为父小波。任何小波变换的基函数，其实就是对这个母小波和父小波缩放和平移后的集合［7］。傅里叶变换适合周期性的、统计特性不随时间变化的信号；而小波变换则适用于大部分信号，尤其是瞬时信号，它针对绝大部分信号的压缩、去噪，检测效果都特别好。

3 试验结果

根据试块中央内腔载荷交变的特征，着重分析有压力的区间内采集到的信号。因为裂纹应该出现在试块中央内腔有负载的区间，而不是卸掉载荷的区间。压力区间外的突发信号是由于试块中央内腔内一直存在空气压缩后膨胀发出的信号。150 MPa压力下声发射传感器采集到的波形时域图以及与之对应的压力曲线如图5所示，对应压力区间内的时域信号如图6所示。

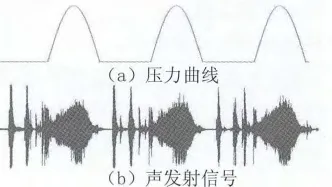
图5 三个循环周期的压力曲线与声发射信号对照

图6 压力区间内的声发射信号时域

图7为有裂纹和无裂纹两种情况下声发射信号的时域及FFT 频域对比图。从图中可以看出，当有裂纹产生时，时域图上压力区间内信号幅值变大了，频域上会发现170kHz以上的高频信号增多，在200kHz附近有明显的峰值出现，并且在300，350，400kHz附近也有较小的峰值出现。这些高频的信号正是在试块冲破漏水前突然出现的，对应着裂纹产生及快速扩展的过程。

图7中的对比信息已经表明，声发射信号的时域图及快速傅里叶变换已经能判断出裂纹的出现及其特征，将图6所示的压力区间的信号进一步进行小波分析，更好地确认裂纹的特征，如图8所示。

图8为压力区间内无裂纹和有裂纹的连续小波变换CWT 结果图。图8（a）是试验开始阶段无裂纹出现时的时频图，大部分信号的频率在100kHz以下，这部分信号主要是试块内腔受到高压冲击以及平台的机械装置噪声引起的。图8（b）中则出现了不少100kHz甚至200kHz以上的信号。这是由于试块中央内腔楔形圆角应力集中处产生了裂纹所引起的变化。可以看出有裂纹产生时，将会出现更高频率的信号，150kHz以上频段出现了较强的突发信号。

接着对信号进行小波分解与重组，分析各频段重组信号特征。图8所示为最初无裂纹时经重组后的200～400kHz及400～600kHz频段的信号。可以看出重组后信号的幅值很小，表明原信号中在200kHz以上高频信号很少。图10所示为有裂纹的信号同频段分解重组图，与图9中高频部分对比，明显看出幅值变大很多，200～400kHz频段是原先无裂纹时的10倍，在400～600kHz频段的幅值达到了无裂纹时的20倍。

图7 两种情况下声发射信号的时域及FFT 频域对比

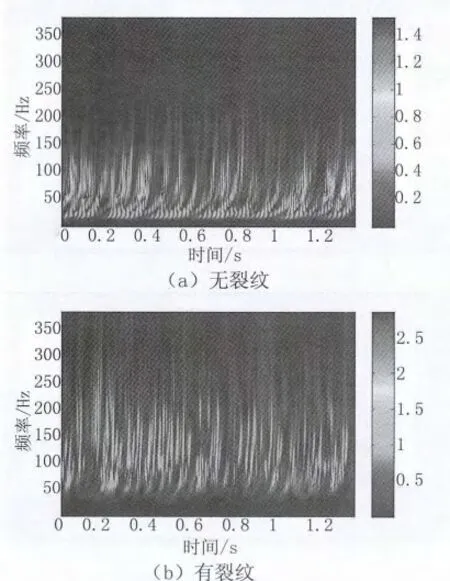
图8 小波变换下的裂纹信息对比

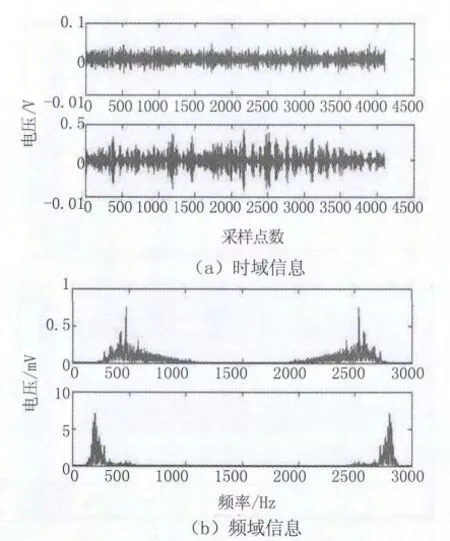
图9 无裂纹信号小波分解重组

分析压力区间内信号波形的电压值在整个试验期间的变化，以压力区间包络下波形的电压值的平方和作为一个参数值，记作Q来表征断裂前后的变化，如表2 所示。由表格数据画出曲线图，如图11所示。

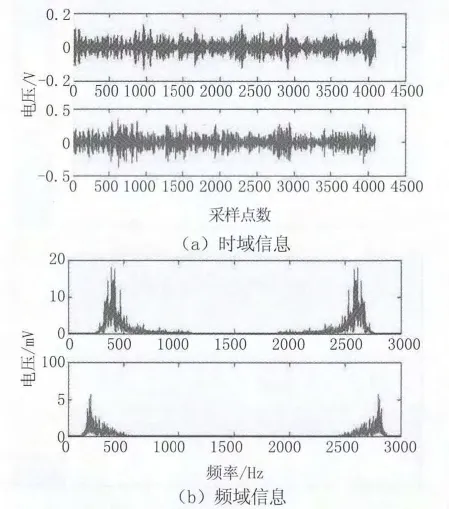
图10 有裂纹信号小波分解与重组

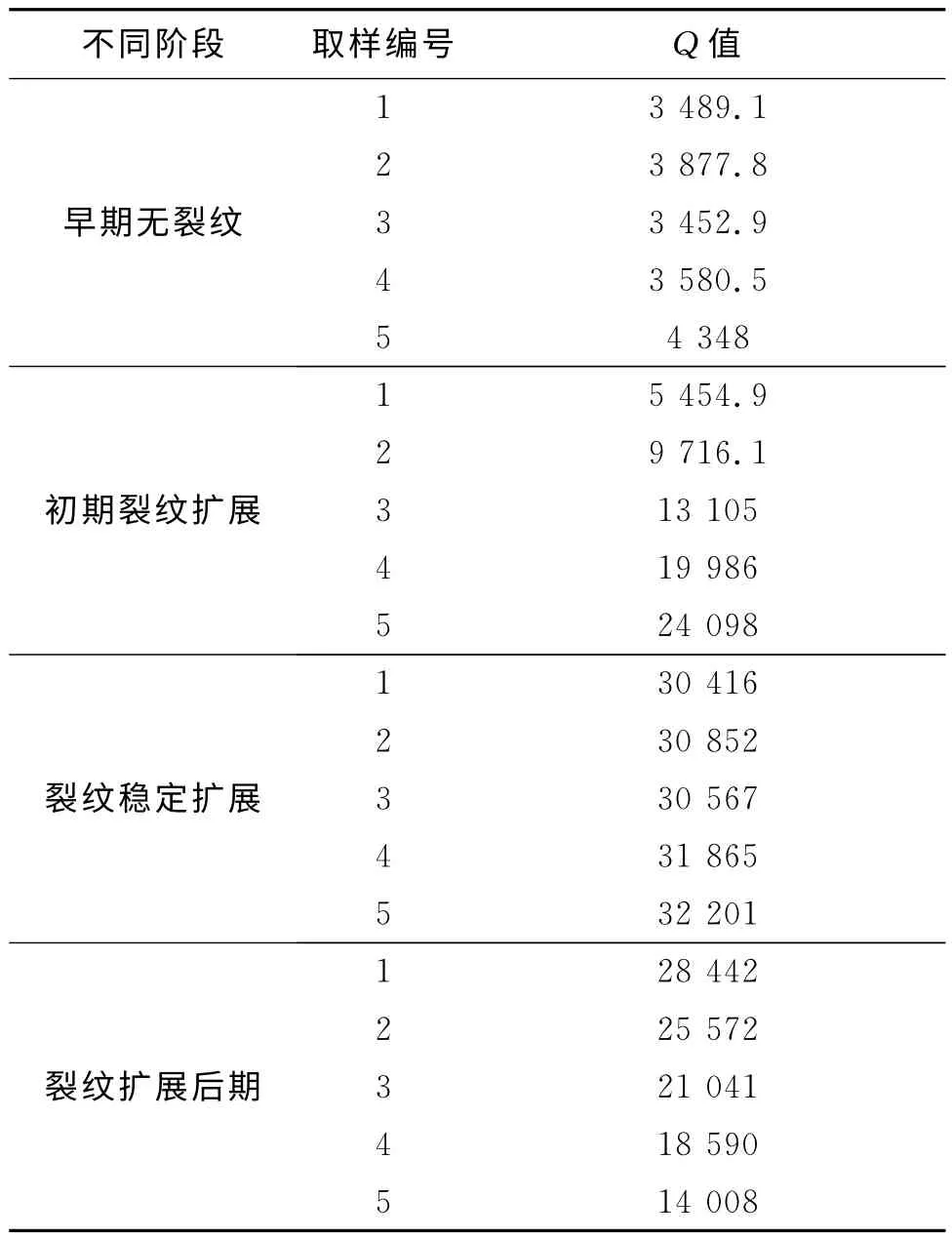
表2 各阶段Q 值

从Q值上可以看出，在早期无裂纹期间，Q值一般在3 500～4 500区间内，当裂纹出现后，Q值明显变大，扩展初期一直增大，到30 000左右，试块破裂后，Q值下降，整个Q值的变化能很好地反应试验期间试块所处的状态。

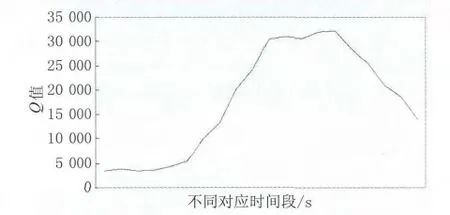
图11 Q 值变化曲线图

Q值作为一个参数，能很好地量化分析信号的特征。因为电压值的大小与信号波形有着密不可分的关系，因此用小波能量系数法来进一步分析信号的特征。

小波能量系数表现了各频率区间内信号的能量分布情况，通过比较各层小波系数的变化，获取裂纹扩展不同阶段的时频特征，建立小波能量系数与裂纹扩展过程之间的对应关系，小波能量系数可以有效地表征裂纹扩展过程中的声发射特征［8］。

根据信号波形的变化将整个试验分为四个阶段：早期无裂纹阶段、初期裂纹出现及扩展阶段、裂纹稳定扩展阶段以及裂纹后期扩展阶段。选取不同阶段的典型波形信号进行分析，选择Daubechies小波作为小波分析的小波基，进行5 尺度下的分解，求取小波分解后各层能量系数，数值列于表3中。根据这些数值画出不同阶段的能量分布柱状图，如图12所示。图12（a）所示为早期无裂纹时的小波能量系数图，可以看出，早期信号波形主要集中在低频阶段，大多数能量集中在d5层，也就是46.875～93.75kHz的频段。到了裂纹初期，会发现d3和d4 层能量系数增大，d5 层明显下降。再到裂纹稳定扩展期，d4 层能量已经超过d5 层，同时，d3和d2层能量也较之前有增加。到后来裂纹扩展后期，d2、d3和d4层能量下降，d5层能量相对增加。整个过程，变化显著的是d3 层和d4 层，也就是93.75～375kHz频段，而跟早期无裂纹时相对比，d3层的变化是最大的，从早期的0.63%到后来的9.1%，13.31%，12.07%，分别增加了13.44，20.13和18.15 倍。说明裂纹的声发射信号集中在d3层频段，也就是187.5～375kHz频段，而这与前面从频谱图以及小波时频图所分析出的结果是一致的。

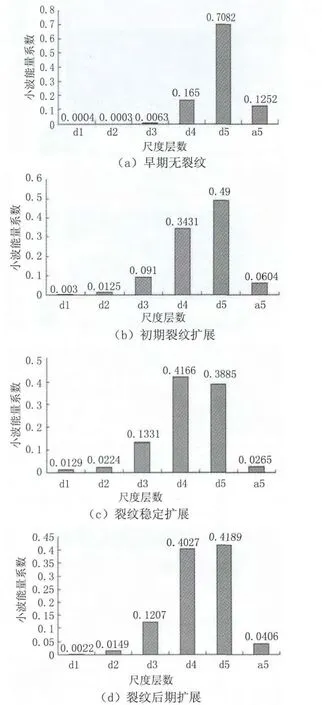
图12 不同阶段小波能量系数分析

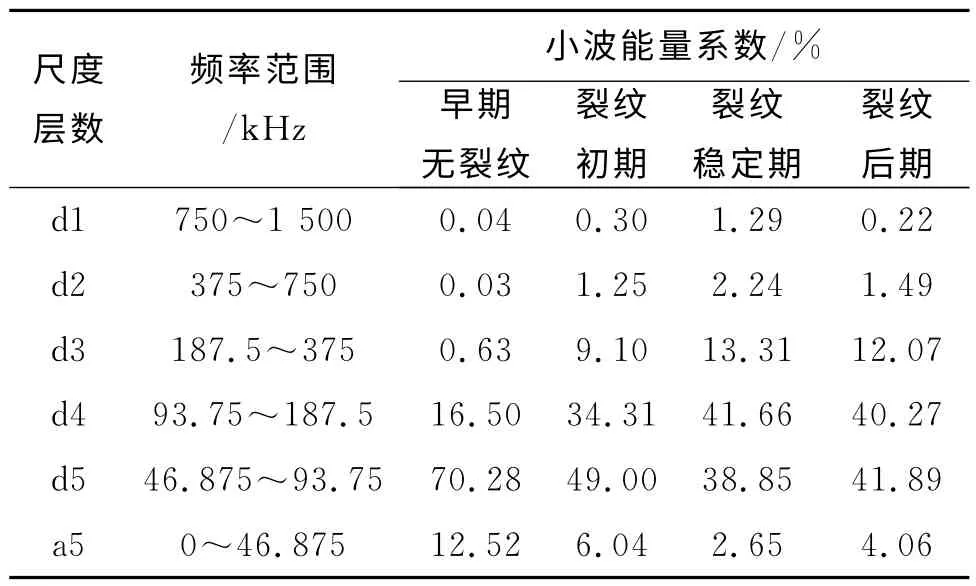
表3 不同阶段各层小波能量系数

综上所述，无论是快速傅里叶变换，还是小波分析手段，在试验中都能有效地区分出试块产生裂纹时的声发射信号。当试块有裂纹出现时，频谱图上会出现明显的高频信号，频率在200kHz以上。经调质处理的Cr－Ni－Mo－V低合金超高强钢材料加工的试块在150MPa交变压力下，试验了53min 45s就产生了裂纹，对比试验过的普通碳钢材料12min失效，则说明了试验的低合金高强钢材料性能更好。