基于FPGA的Systolic乘法技术研究*
2015-01-09周磊涛陶耀东
周磊涛,陶耀东,刘 生,李 锁
(1.中国科学院大学,北京 100039;2.中国科学院沈阳计算技术研究所,辽宁 沈阳 110168;3.沈阳高精数控技术有限公司,辽宁 沈阳 110168)
基于FPGA的Systolic乘法技术研究*
周磊涛1,2,陶耀东2,刘 生1,2,李 锁3
(1.中国科学院大学,北京 100039;2.中国科学院沈阳计算技术研究所,辽宁 沈阳 110168;3.沈阳高精数控技术有限公司,辽宁 沈阳 110168)
Systolic乘法是一种基于SIMD-MC2模型的矩阵乘算法,无法直接应用在单独的嵌入式系统中,所以提出一种采用FPGA技术实现Systolic乘法的方法。该方法将FPGA的硬件并行特性与巧妙的并行算法结合起来,利用FPGA灵活可编程的特点,在FPGA内部设计了一种基于MC2模型的节点阵列来实现Systolic乘法。实际应用中,可以灵活地修改节点单元的数量和节点的功能来满足不同规模的运算矩阵需求并充分利用FPGA的资源。仿真结果验证了该方法的正确性。实际测试结果表明:该方法具有较快的速度和较高的实时性。
矩阵乘法;现场可编程门阵列;Systolic乘法;并行计算
1 引言
矩阵乘法在科学计算、数字信号处理和图像处理等领域起着非常重要的作用,其计算性能直接影响到系统的整体性能,所以采用有效的矩阵乘法算法,降低矩阵乘法计算时间,具有非常重要的实际工程意义。通常的矩阵乘运算采用串行计算方法,其计算复杂度(通常为O(N3))难以满足计算实时性的要求,所以采用并行计算的方法来求解矩阵乘法是近年来发展的方向。在并行计算机系统下,为了实现并行计算,需要将数据划分给不同的处理器,并出现了许多性能优异的并行矩阵乘算法,比较著名的有DNS算法[1,2]、Cannon算法[2,3]、FOX算法[2,3]、Systolic乘法[3]等,但是这些算法需要多处理器甚至是多计算机才能完成,无法直接应用到单独的系统中,例如嵌入式系统、数据处理板卡等。
近年来,现场可编程门阵列FPGA(Field Programmable Gate Array)器件取得了飞速的发展,其以可编程特性、细粒度并行能力、丰富的逻辑资源、灵活的算法适应性、低硬件代价和高性能低功耗比成为理想的可编程系统平台。另一方面,由于矩阵乘法运算自身具有良好的并行性,采用FPGA技术来加速矩阵乘法计算是一种最好的选择。本文将FPGA技术与并行矩阵乘算法结合起来,但在众多并行矩阵乘算法中,DNS算法是面向立方体的处理器结构,当阶数大于2时,此结构难以表示;Cannon算法源于空间对准的思想,但需要在节点(Node)单元中预先置入分配好的数据,此过程处理难度大,不容易实现;FOX算法和Cannon算法类似;Systolic乘法源于时间对准的思想,分配好的数据可直接按行列输入到节点中,容易实现,所以本文设计实现了基于FPGA的Systolic乘法。
目前,使用FPGA实现Systolic矩阵乘法已经取得一些研究成果,在矩阵向量乘法方面, Karra M Ch 等人[4]在FPGA上实现了基于Systolic结构的矩阵向量乘法,使计算时间复杂度降为N1+N2+1(N1为被乘矩阵行数,N2为乘矩阵行数),但需要在初始化阶段预先为计算节点赋初值,不容易实现。在矩阵乘法方面, Horita T等人[5]提出了具有容错机制的二维Systolic结构矩阵乘法,使用了可重配置的开关网络,减少了矩阵乘法的规模,但不适合小规模数据量的嵌入式系统。Sonawane D N 等人[6]提出了使用四个处理节点,轮流分发矩阵行列数据的方法,降低了逻辑资源占用,提升了计算性能。但是,当矩阵规模变化时,其计算性能随之变化,而且需要同时改变控制逻辑,通用性不好,限制了此方法的使用。Vucha M等人[7]利用FPGA实现了一种Systolic阵列结构的矩阵乘法,取得了比较好的计算性能,但扩展性差,不适合灵活变化的嵌入式系统。综上所述,以上研究都不适合在嵌入式系统中使用。
本文设计实现了一种具有较高计算性能,且具有良好扩展性的基于FPGA的Systolic算法的矩阵乘法器,其简单、模块性好且易重配置的特点特别适合应用在嵌入式系统中。该乘法器最大程度使用了FPGA自身的专用乘法硬核,减少对逻辑资源的占用,提高了计算性能。通过对不同情况下矩阵乘法的分析,证实了本矩阵乘法器的计算性能。
2 Systolic阵列
1978年Kung H T博士[8]提出了Systolic阵列,源于时间对准的思想,以其能充分利用硬件的专用并行结构,巧妙地以空间换时间的硬件实现方法,具有流水线结构和SIMD阵列结构的优点,能获得较高的时间和空间并行性,得到了广泛的研究和应用。
Systolic阵列是一个由一些具有预定功能的节点有规则地互联起来的专用并行系统[9]。图1所示是阵列中的数据流动的一个方向,数据从存储器(MEM)中以一定的规律顺序流出后,进入阵列中某一个方向的第一个节点,经过节点处理后,将新的结果流向同一个方向的下一个节点,并依此反复直到从最后一个节点流出的数据返回到存储器。这样的工作机制很像从心脏流出的血液经过顺序处理后又流回心脏中,所以Systolic阵列又译为“心动阵列”[8,10]。为了更好地利用Systolic阵列的并行性,阵列中可以存在多个方向、不同流动速度的数据流,这样可以得到相当高的系统数据吞吐量。Systolic阵列采用简单的通信机制,数据在节点之间以流水线方式传递,并且整个阵列按同步方式工作;另外,Systolic阵列具有简单、规整、模块性好的特点,只有少量的节点与外部有IO操作,这能使系统保持较好的处理速度,同时也可与外部IO带宽之间的平衡,非常适合FPGA实现。

Figure 1 Principle of Systolic array
3 Systolic乘法思想
Systolic乘法是基于Systolic阵列结构的并行矩阵乘法,通过在时间上延迟矩阵输入元素的方法来达到一对下标合适的矩阵元素就地相乘的目的[11]。
3.1 并行算法描述
在SIMD-MC2模型上的Systolic乘法算法如下:
输入矩阵A、B:Am*n、Bn*k。
输出矩阵C:Cm*n在P(i,j)中存在有乘积矩阵元素Cij。
/*其中P(i,j)为阵列第i行第j列计算节点,Cij为P(i,j)的计算结果*/
Begin
Fori=1 tompar-do
Forj=1 tokpar-do
Cij⟸0
WhileP(i,j) receives two inputsaandbdo
Cij⟸Cij+a*b
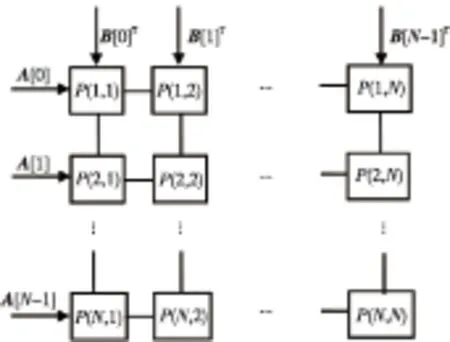
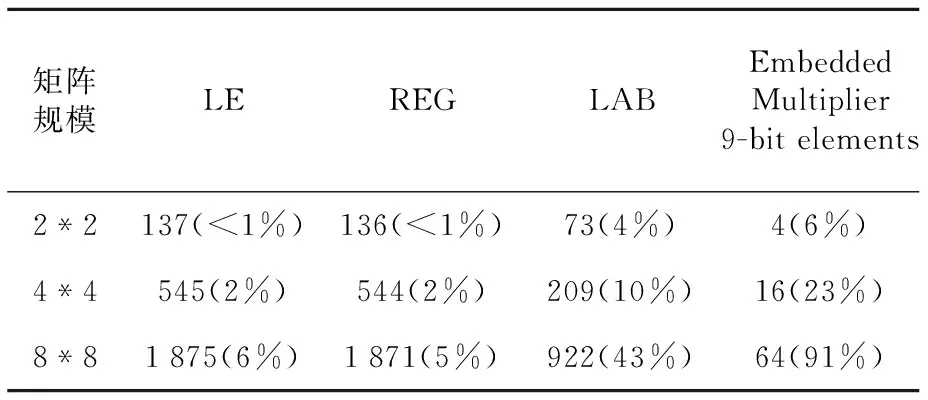
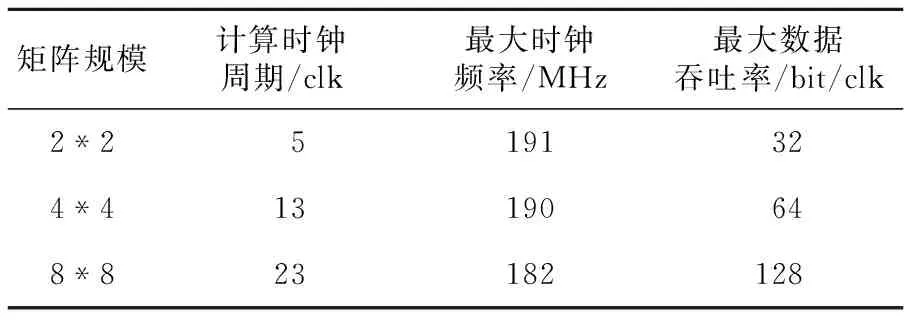
if(i if(j end while end for end for End 3.2 数据输入规则 设输入矩阵Am,n和Bn,k,输出为Cm,k,C=A*B。 A矩阵的行向量按行号输入到对应的阵列行,向量中的每个数据按列号从大到小依此进入阵列的行。其中第i行输入的向量中第j个数据和第i-1行输入向量中第j-1个数据同时进入阵列。B矩阵的列向量按列号输入到对应的阵列列,向量中每个数据按行号从大到小依此进入阵列的列。其中,第i列输入的向量中第j个数据和第i-1列输入向量中第j-1个数据同时进入阵列。当行列输入的数据汇合到节点时,进行相乘运算。一个3阶Systolic乘法的示例如图2所示。 Figure 2 An instance of Systolic multiplication 3.3 数据在阵列中流动规则 (1)Aij按照行号从小到大的顺序依次穿越第i行节点单元;Bij按照列号从小到大的顺序依次穿越第j列节点单元;Aij和Bij在同一时钟控制下,直至A、B所有元素穿越节点单元阵列的整行和整列。 (2)Aik和Bkj同时到达P(i,j)时相乘并加入Cij中,Cij=∑Aik*Bkj(k=0,1,…,n-1)。 4.1 节点单元设计 节点是构成Systolic乘法的基本单元,可以通过修改节点中的逻辑功能,实现不同场合下Systolic乘法。其主要由一个乘法器、一个加法器和一个用于存储计算结果的寄存器构成。 其内部结构如图3所示,图中Row_in与Col_in为节点的输入数据,clk为同步时钟,rstn为异步复位信号,每次重新计算矩阵乘之前需要复位清除节点内所有的数据。在同步时钟的控制下,Row_in与Col_in为乘法器的两个输入数据,数据相乘的结果作为累加器的一个输入,REG是节点内的存储单元,用于记忆上一次累加的结果,并作为累加器的另一个输入数据,累加器将数据相乘的结果和REG中的数据相加,并将结果再写入REG完成一次乘累加过程。当阵列中的节点再无输入数据时,节点的REG中的数据就是最后计算的结果。 在节点输入数据乘累加的同时,将刚接受的数据分别输出到对应行列的下一个节点,即Row_out与Col_out。 Figure 3 Architecture of the nodes 4.2 并行矩阵乘法器设计 Systolic乘法中节点以普通的二维网孔互联,阵列的节点规模可以根据相乘矩阵的大小和FPGA芯片的资源情况进行调整,假设FPGA中有N2个节点,将节点排列成如图4所示的N阶阵列形式,阵列中首个行节点和列节点作为系统的输入接口,每个节点有最终数据输出接口,这样可以使先计算好的节点结果输出到IO端口,有利于流水线处理[8]。 按照Systolic乘法思想,节点P(1,1)是第一个数据汇合的节点,依此是节点P(1,2),P(2,1),可知数据的流动过程是从左上角开始向右下角方向流动的,又根据输入时间延迟的特点可知,节点P(1,1)是结束数据输入的第一个节点,节点P(N,N)是最后一个结束计算的节点。所以,Systolic乘法一次矩阵乘计算总共需要计算的时间是从P(1,1)接受数据到P(N,N)结束计算数据,以N阶阵列为例,总时间为3*N-1,计算时间复杂度为O(N)。 Figure 4 Structure of Systolic multiplication array 5.1 仿真验证 用于仿真的两个4*4的8bit矩阵作为输入实例,阵列规模为4阶矩阵,用VerilogHDL语言编程,并在QuartusII综合设计软件中进行仿真,图5为仿真结果。 Figure 5 Simulation results of Systolic multiplication 图5中ina为被乘矩阵,inb为乘矩阵,其中result值为节点计算的结果,图中选择了最后一个完成计算的节点P(3,3),可以看出经过从数据的输入到矩阵完成乘法运算总共使用了11个时钟周期,与3*N-1的结果吻合。 5.2 实验验证 实验在Altera DE2开发板上完成了实际测试。开发板使用了具有5000LEs的Cyclone II EP2C35F672C6 FPGA芯片。用Quartus II 综合设计平台进行编译,仿真验证的基础上,将综合生成的配置文件下载到FPGA芯片中,为了便于验证结果,在设计中为每行、每列添加了一个数据流生成模块(会占用一定的FPGA逻辑资源),并使用在Quartus II中集成的Signaltap II在线逻辑分析仪进行FPGA片上调试。实验使用两个4*4矩阵8 bit矩阵作为实例,在FPGA中使用了4阶Systolic阵列结构。Signaltap II调试结果如图6所示,在复位信号上升沿捕捉到了各行列输入的结果,result值为矩阵运算最后一个节点输出结果,经过11个周期,其输入结果与实际的矩阵运算结果完全吻合。 Figure 6 Experimental results of Systolic multiplication 5.3 FPGA内部资源使用情况 使用Quaruts II软件进行适配,是将综合工具产生的网标文件,针对当前的目标器件执行包括底层逻辑配置、逻辑分割、逻辑优化、逻辑布局布线等逻辑映射操作,产生最终的编程下载文件。表1所示为8 bit不同规模的矩阵相乘的资源占用情况。 Table 1 Resource usage of FPGA表1 FPGA资源使用情况 由表1中的结果可知,FPGA内部资源的占用情况与Systolic乘法阵列中节点数量成正比。由于在设计中每一个节点使用了一个FPGA自带的内嵌专用乘法硬核,所以减少了对逻辑单元LE(Logic Elements)的占用,当FPGA中内置64个节点时,设计占用了91%的内嵌专用乘法硬核,而只占用了大约6%的LE,这样既能充分利用FPGA资源,也提升了矩阵乘法的计算性能。 5.4 性能分析 本文通过对2*2阵列、4*4阵列、8*8阵列的Systolic乘法实例进行分析,得到如表2所示的结果。 Table 2 Performance of Systolic multiplication表2 Systolic乘法计算性能 由表2可知,基于FPGA的Systolic乘法的计算时间与矩阵规模成线性关系,而且能达到很高的时钟频率。设计中每个时钟的最大数据吞吐量与矩阵的行列输入节点数量有关,根据Systolic乘法中输入规则,当所有的行列输入节点都有输入数据时,能达到最大的输入数据量,所以本设计输入时间与矩阵规模成线性关系,可以快速实现数据输入。 5.5 与串行矩阵乘法器比较 通过在Altera DE2开发板上实际测试Systolic乘法的执行时间,并与串行矩阵乘法器执行时间的最优理论值进行比较(完成一次乘法运算与加法运算各为1个时钟周期)。从表3中可以看出,Systolic乘法的计算时间明显少于串行矩阵乘法器,达到了较好的加速效果。 Table 3 Execution time comparison of Systolic multiplication and Serial matrix multiplication表3 Systolic乘法与串行矩阵乘法执行时间比较 本文对应用在并行处理计算机系统中的Systolic乘法进行介绍和分析,并采用FPGA技术实现了这一算法。通过在Quartus II综合开发软件上设计并仿真验证了该方法的逻辑正确性,并在Altera DE2开发板上进行了实际测试,对该方法的性能与资源占用情况进行了分析,并与串行矩阵乘法器在计算时间上进行了比较。实验结果表明该方法可以达到非常好的综合性能,特别适合作为一个模块应用于需要实时性矩阵乘计算的嵌入式系统中,有非常好的加速效果。 [1] Dekel E,Nassimi D,Sahni S. Parallel matrix and graph algorithms[J]. SIAM Journal on Computing,1981,10(4):657-675. [2] Chen Guo-liang.Parallel computing:Architecture,algorithm,programming[M].3rd Edition. Beijing:Higher Education Press,2009.(in Chinese) [3] Chen Guo-Liang. Design and analysis of parallel algorithms[M].3rd Edition. Beijing:Higher Education Press,2009. (in Chinese) [4] Karra M C,Bekakos M P,Milovanovic I Z,et al. FPGA implementation of a unidirectional Systolic array generator for matrix-vector multiplication[C]∥IEEE International Conference on Signal Processing and Communications,2007:1. [5] Horita T,Takanami I.An FPGA-based fault-tolerant 2D Systolic array for matrix multiplications[M]∥Transactions on Computational Science,2011:108-124. [6] Sonawane D N,Sutaone M S,Malek I. Systolic architecture for integer point matrix multiplication using FPGA[C]∥Proc of the 4th IEEE Conference on Industrial Electronics and Applications,2009:3822-3825. [7] Vucha M,Rajawat A. Design and FPGA implementation of Systolic array architecture for matrix multiplication[J]. International Journal of Computer Applications,2011,26(3):18-22. [8] Kung H T. Why Systolic architectures[J]. IEEE Computer,1982,15(1):37-46. [9] Zheng Fei,Xie Kang-lin.Systolic array and the algebraic specification of the Global view[J]. Computer Engineering and Science,1992,4(3):25-32.(in chinese) [10] Guerra C,Melhem R G. Synthesis of Systolic algorithm design[J]. Parallel Computing,1989,12(2):155-207. [11] Wan C R,Evans D J. Nineteen ways of Systolic matrix multiplication[J]. International Journal of Computer Mathematics,1998,68(1-2):1-2. 附中文参考文献: [2] 陈国良. 并行计算——结构·算法·编程(·第三版·)[M].北京:高等教育出版社,2009. [3] 陈国良. 并行算法的设计与分析(·第三版·)[M].北京:高等教育出版社,2009. [9] 郑飞,谢康林. Systolic阵列及其全局视图的代数描述[J]. 计算机工程与科学,1992,14(3):25-32. 周磊涛(1990-),男,河南鹿邑人,硕士生,研究方向为嵌入式系统与数控技术。E-mail:zhoult@mail.ustc.edu.cn ZHOU Lei-tao,born in 1990,MS candidate,his research interests include embedded system, and control technology. Research on Systolic multiplication technology based on FPGA ZHOU Lei-tao1,2,TAO Yao-dong2,LIU Sheng1,2,LI Suo3 (1.University of Chinese Academy of Sciences,Beijing 100039;2.Shenyang Institute of Computing Technology,Chinese Academy of Sciences,Shenyang 110168;3.Shenyang Golding NC Tech. Co.,Ltd.,Shenyang 110168,China) Systolic multiplication is an algorithm based on the SIMD-MC2model, but it cannot be applied in the embedded system directly. We propose an implementation of Systolic multiplication by FPGA technology, which combines the hardware parallelism of the FPGA and the parallel algorithm together. To realize Systolic multiplication, we design a node array based on the MC2model inside the FPGA by making use of the flexible and programmable features of the FPGA. In practical applications, the number and function of the nodes can be modified flexibly to meet the needs of different scale matrixes and the FPGA resources are fully utilized. Simulation results verify the proposed method, and the actual test results show that this method has a faster speed and a higher real-time performance. matrix multiplication;field-programmable gate array;algorithm of Systolic;parallel computing 1007-130X(2015)09-1632-05 2014-03-20; 2014-06-20基金项目:国家科技支撑计划沈阳特种专用数控机床产业集群国产数控系统创新应用示范(2012BAF13B08) TP303 A 10.3969/j.issn.1007-130X.2015.09.005 通信地址:110168 辽宁省沈阳市东陵区南屏东路16号 Address:16 Nanping Rd East,Dongling District,Shenyang 110168,Liaoning,P.R.China
4 Systolic乘法实现

5 实验和性能分析



6 结束语

