蔗糖蒸发结晶过程的数学建模

杨丹丹

（国家知识产权局专利局专利审查协作广东中心，广东 广州 510530）

0 前言

煮糖过程的目的是尽可能充分析出糖膏中的糖分，获得符合国家白砂糖标准［1］的粒度均匀、洁白干燥的蔗糖晶体。因此煮糖过程操作的好坏不仅会影响到蔗糖产品的质量和数量，而且还将影响到整个生产系统有关物料的平衡［2］。煮糖过程［3，4］是利用在煮糖结晶罐中糖膏在不同过饱和度下的特性，控制过饱和度在适当的范围内，糖膏中结晶逐渐析出蔗糖晶体的过程。煮糖结晶过程是一个包含锤度、粘度、温度、过饱和度、真空度等多个因素的生产过程［5，6］。目前国外对蔗糖蒸发结晶过程的数学建模的研究较深入［7～11］，相比之下，国内相关研究非常少。

在本文中研究蔗糖蒸发结晶过程的数学模型，包括蔗糖结晶颗粒粒度、结晶糖量、浓度、晶体生长速度在煮糖过程中呈现的特性。蔗糖晶体生长的动力学研究对于工业结晶罐的设计与管理起着非常重要的作用。实验用的动力学数据以后也可能应用于工业实际中。本文的研究内容打开了新的见解与思路，能够更好的了解蔗糖结晶过程。

1 蔗糖结晶颗粒CSD的数学模型

1.1 建立CSD的数学模型

结合CSD的直方图密度分布图与累积分布图，建立CSD的对数正态分布的数学模型。蔗糖结晶颗粒CSD概率密度分布函数q0（Deq）与累积分布函数Q0（Deq）的数学模型分别为式（1.1.1）、（1.1.2）、（1.1.3）：erf（·）为误差函数。

1.2 CSD数学模型的仿真结果

对CSD数学模型的仿真结果见图1，包括直方图、密度分布曲线、累积分布曲线的仿真结果。从图1可以看出，提出的蔗糖结晶颗粒CSD的概率密度分布函数与累积分布函数的数学模型很好地拟合了真实的CSD。

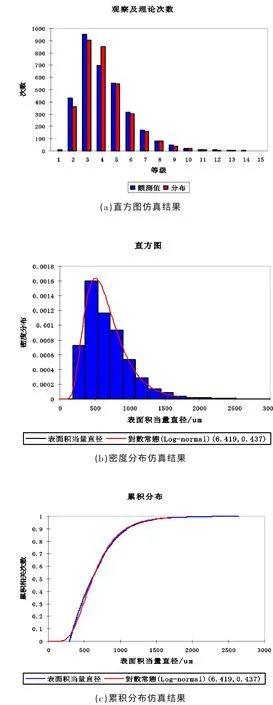
图1 CSD数学模型的仿真图 （a）直方图仿真 （b）密度分布仿真 （c）累积分布仿真

2 结晶糖量与表面积当量直径关系的数学模型

为了研究粒度、结晶糖量对煮糖过程的影响，采用质量平衡方法与图像分析方法来对晶体表面积当量直径与结晶糖量之间数理关系进行数学建模，能够更好的了解蔗糖结晶过程。

2.1 质量平衡法与图像分析法

2.1.1 质量平衡法

根据质量平衡方法［12～14］，蔗糖晶体的表面积当量直径与质量之间的关系为（α取值为0.75）：

结晶罐内的晶体数量计算如下［12,13］（α取值为0.31）：

ms/kg为种糖质量，L0为种子晶粒体积当量直径，取值为13.33μm。ms=52g，N=7.25×105粒。质量平衡法对Deq与mc之间数理关系的数学模型为式（2.1.3）：

2.1.2 图像分析法

蔗糖晶粒的质量与表面积的关系根据文献［14］：

式中mc为每颗蔗糖晶粒的质量，单位为mg，S为每颗蔗糖晶粒的表面积，单位为m2。经过单位量纲之间的换算，本文的图像分析方法对Deq与mc之间数理关系的数学模型为式（2.1.5）：

2.2 两种数学模型的仿真结果比较

图像分析与质量平衡计算的结晶糖量与表面积当量直径之间数理关系的模型见图2。两种方法得出的曲线很相似，等同度很高。因此，图像分析得出的结果是可靠的。数据来自样本集P1的随机抽样300例。

图2 图像分析与质量平衡计算的表面积当量直径比较

2.3 从浓度分布模型估计溶解度

通常一些有关溶解度与温度的实验方程适用于大部分普通的溶液，这在制糖工业是得到普遍认知的。在某个给定温度的溶解度可以通过实验来获得，使得晶体生长或溶解直到饱和，测量这个温度下的溶液浓度，但受到操作者知识与技术器材的限制。文献［7］提出一个新的办法，在正常的结晶条件下能够快速应用。一个典型的结晶曲线见图3所示。溶液的浓度开始于Ci，并不断下降趋近饱和，用点c*处的浓度来代表溶解度［7，14］。

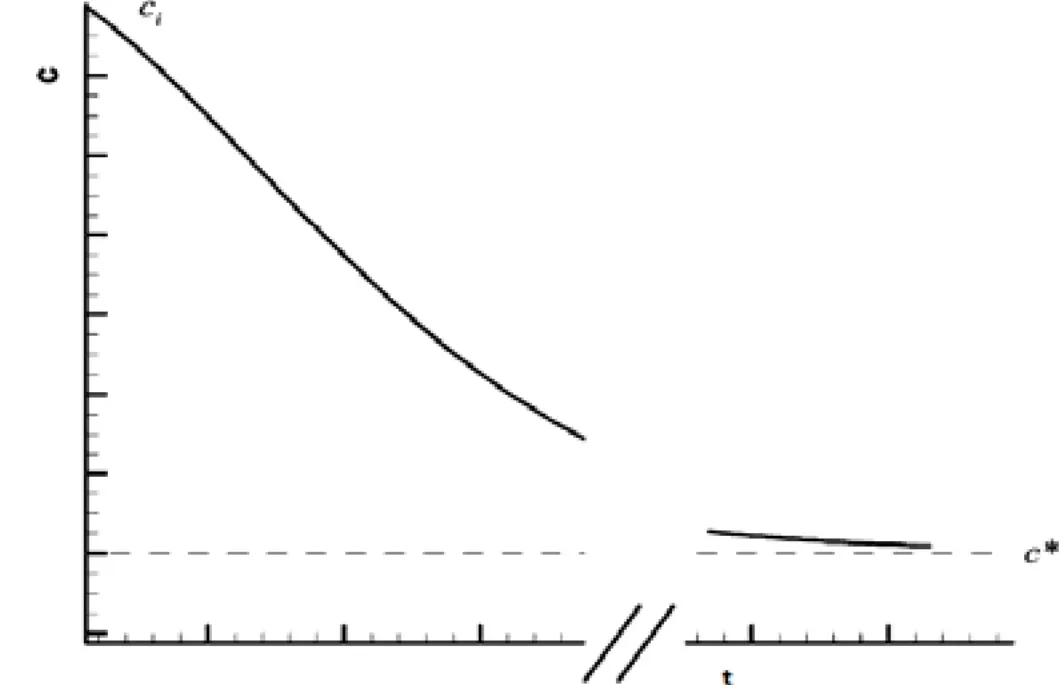
图3 结晶曲线［7］

以下的分析［7］基于假设水的质量mw为恒定值，这使得含水量的自动控制是有效的。溶液浓度c表示为溶液质量除以水的质量，于是浓度的变化可以很容易与晶体质量mc、时间t联系起来，见下式：

若没有成核现象，则每单位面积时间下的晶体质量增长遵循生长规律，通常定义为：

k与r为动力学参数，r=2。结合以上两个式子得出：

这个方程在获得晶体表面积A与时间t的关系后可以得到数值解。不过更为方便的方式为用解析解来拟合实验数据得到c*。出于这个目的，用一个生长周期内的恒定平均晶体表面积 来简化式子。简化式子如下：

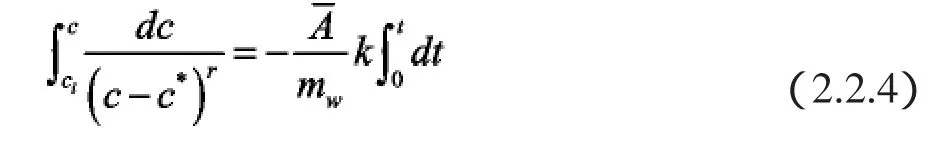
得出浓度分布曲线如式：

建立煮糖过程浓度与时间的数学模型如式（2.2.7）：

模型拟合结果见图4。从结果中看出，开始浓度ci=（301.5kg蔗糖）/（100kg水）。溶解度c*=（260 kg蔗糖）/（100kg水），见虚线处。模型拟合结果与实验测量结果很相近。

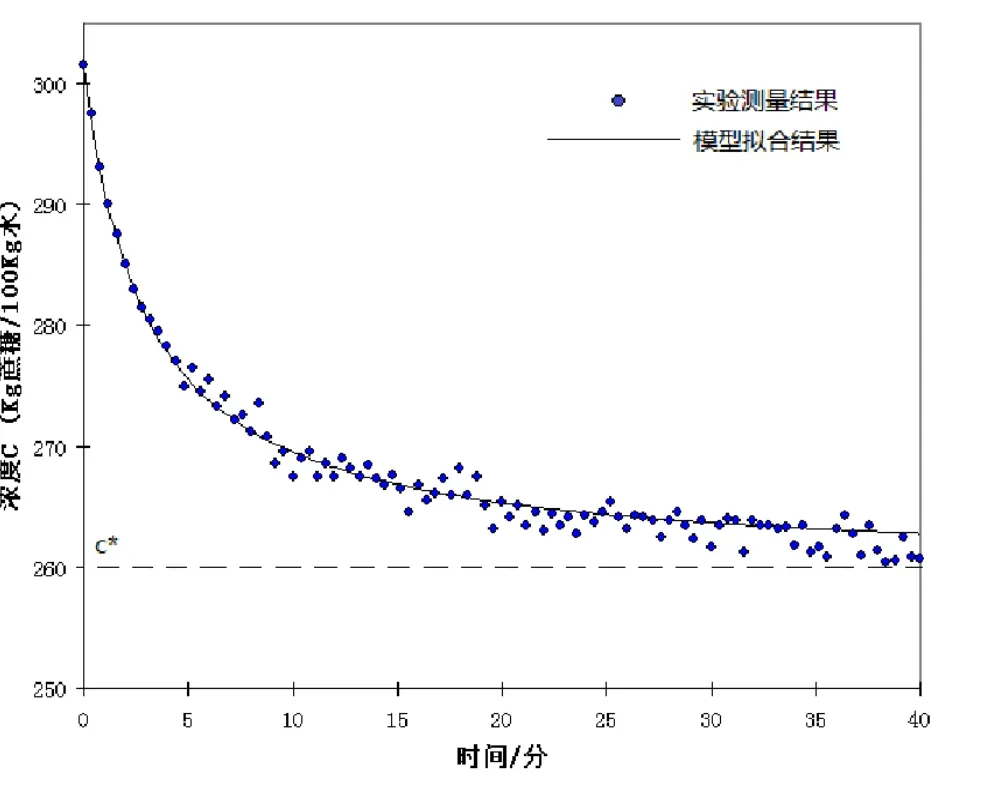
图4 浓度分布与时间数学模型仿真

2.4 晶体生长动力学的模型研究

2.4.1 晶体质量与时间关系的数学模型

采集来自实验研究用的50L煮糖罐的蔗糖生长实验数据。见表1所示。

根据表1，建立晶体质量与时间的数学模型如式（2.3.1）：

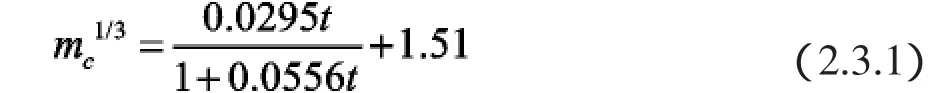
模型仿真结果如图5所示。从图中可以看出，模型仿真的结果与实验测量的数据分布拟合效果较好，模型的分析是可靠的。

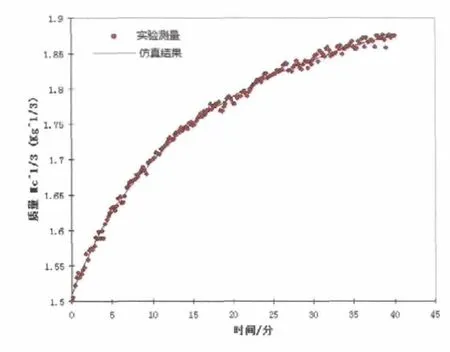
图5 晶体质量与时间数学模型仿真

2.4.2 晶体质量生长速度与过饱和度关系的数学模型

煮糖过程中的过饱和度［7，14］需要预先知道溶液溶解度的情况，由于非蔗糖混合物的数量及其变化范围之广使得准确测量过饱和度存在困难。蔗糖晶体生长的动力学研究对于工业结晶罐的设计与管理起着非常重要的作用。实验用的动力学数据以后有可能应用于工业中。在本小节中研究晶体生长动力学的数学模型。其中，溶液浓度、晶体质量随着时间而改变的信息必须是可用的，其他的先验知识包括蔗糖溶解度、晶体参数例如颗粒个数与形状因子等等。

蔗糖晶体的质量生长速度Rg通常定义为在单位时间和单位晶体面积内的质量改变量［7］：

现在计算生长速度的实验方法采用在一个很小的时间区间△t内质量的增长量△mc来计算Rg。在这种情况下，晶体表面积需要假设在这个时间段内维持常量或者用平均表面积来代替。晶体表面积表示为［7］：

代入式（2.3.2），得到［7］：

归纳为式（2.3.5）［7，13］：（α=0.64［13］，β=4.52［13］，pc=1590kg/m3［7，13，14］）：

在这里，过饱和度定义为S=c-c*，c*为前面的溶解度。根据蔗糖质量与时间关系的数学模型，浓度分布数学模型，得到：

因此建立蔗糖晶体质量生长速度与过饱和度之间的数学模型，见式（2.3.8）：

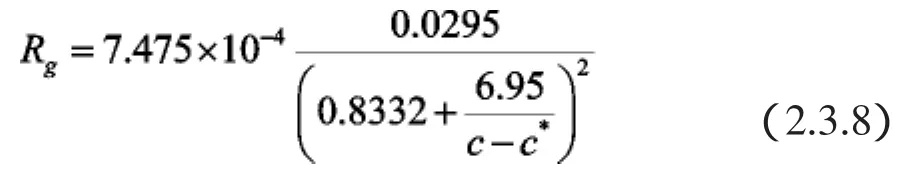
质量生长速度值为2.2（×105kg/（m2·s））。模型仿真的曲线如图6所示。这个动力学曲线代表了过饱和度对晶体质量生长速度的影响。

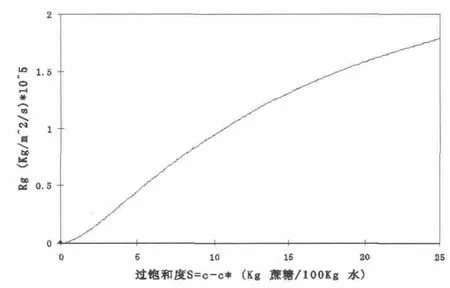
图6 晶体质量生长速度与过饱和度数学模型仿真

2.4.3 晶体线性生长速度与过饱和度关系的数学模型

线性生长速度G与质量生长速度Rg之间存在这样的关系［7］：

建立线性生长速度与过饱和度之间的数学模型如式（2.3.10）：

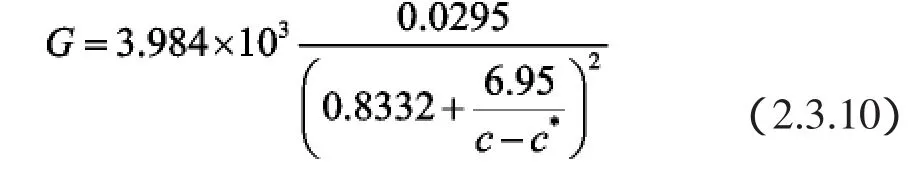
线性生长速度为117（μm/h）。模型仿真结果见图7。这个动力学曲线代表了过饱和度对晶体线性生长速度的影响。

图7 线性生长速度与过饱和度数学模型仿真

在阅读外国相关文献后，统计不同文献中蔗糖蒸发结晶过程中蔗糖晶体的线性生长速度与质量生长速度值，见表2。从表中可以看出，本文提出的模型计算得出的线性生长速度与质量生长速度值与其他国外文献值是一致的，证明了两种模型的仿真结果是有效可靠的。

表2 不同文献中蔗糖蒸发结晶过程线性生长速度与质量生长速度值［7］

3 小结

本章对蔗糖蒸发结晶过程进行数学建模研究。结合前面章节中提出的图像分析方法与本章的数学建模方法打开了新的见解与思路，能够更好的了解蔗糖结晶过程。首先建立蔗糖结晶颗粒CSD的对数常态分布数学模型并对真实的样本进行拟合，并通过模型进行原点矩与置信区间的计算，通过仿真结果、对颗粒粒度的MA、CV、总长、总表面积、总质量等参数结果的比较，本文建立的CSD模型逼近真实的CSD。然后分别用质量平衡法与本文中的图像分析法建立结晶糖量与表面积当量直径关系的数学模型。通过两种仿真结果比较，图像分析法建立的模型与质量平衡法建立的模型等同度高，模型可靠。最后，对煮糖过程中溶解度及其生长动力学相关参数的数学模型进行研究。在浓度分布模型中估计出溶解度、从质量平衡中估计质量与时间关系的模型的基础上，分别对晶体质量生长速度、线性生长速度与过饱和度之间关系的模型进行研究。计算出线性生长速度与质量生长速度值，在国外相关文献计算的值的范围之内，证明了建立的动力学模型是可靠的。

［1］ GB317-2006，白砂糖［S］.

［2］ 李琳.蔗糖结晶连续化的问题与措施［J］.甜菜糖业，1990（1）：22-27.

［3］ 蔗糖结晶与煮炼系统［DB/OL］.中国糖业交易网，http：//www.ec-sugar.com/web/index.jsp.

［4］ 黄铨章，李尔煊.微机煮糖与“五一”煮糖法［J］.甘蔗糖业，1984（3）：1-4.

［5］ 黄春侠.间歇煮糖自动化控制的研究［D］.兰州：兰州理工大学，2007.5.

［6］ 魏立.基于自适应评价设计方法的蔗糖结晶过程的优化控制［D］.南宁：广西大学，2009.6.

［7］ Pedro M.Martins&Fernando A.Rocha.Modeling Sucrose Evaporative Crystallization.Part 2.Investigation into Crystal Growth Kinetics and Solubility ［J］.Ind.Eng.Chem.Res.2005，44，8865-8872.

［8］ P.Quintana-Herna’ndez.Mathematical Modeling and Kinetic Parameter Estimation in Batch Crystallization，2004 American Institute of Chemical Engineers［J］.AIChE Journal July 2004 Vol.50，No.7：1407-1417.

［9］ N.Faria&S.Feyo de Azevedo.Modelling agglomeration degree in sucrose crystallization ［J］.Chemical Engineering and Processing 47（2008）1666-1677.

［10］Wright，P.G.Pan and Pan Stage Control［J］.Sugar Technol.Rev.1983，10，39-76.

［11］Miller，K.F.Broadfoot，R.Crystal Growth Rates in High Grade Massecuite Boilings［J］.Proc.Int.Soc.Sugar Cane Technol.（Australia）1997，441-447.

［12］Pedro M.Martins&Fernando A.Rocha.Modeling Sucrose Evaporative Crystallization.Part 1.Vacuum Pan Monitoring by Mass Balance and Image Analysis Methods［J］.Ind.Eng.Chem.Res.2005，44，8858-8864.

［13］A.Ferreira&N.Faria.Using an Online Image Analysis Technique to Characterize Sucrose Crystal Morphology during a Crystallization Run ［J］.Ind.Eng.Chem.Res.2011，50：6990-7002，ACS Publications@2011 American Chemical Society.

［14］陈维钧，许斯欣等.甘蔗制糖原理与技术第四分册蔗糖结晶与成糖［M］.北京，中国轻工业出版社，2001.

［15］G.R.E.Lionnet.An Interfacial Model for The Transfer of Impurities Into The Sucrose crystal ［J］.Institution of Chemical Engineers，Trans IChemE，1998（76），Part A.