MathCAD在交通标志支撑结构优化设计中的应用

林 枫，廖秀斋

（温州设计集团有限公司，浙江温州 325000）

1 概述

在交通标志结构设计中，由于各地地质、气候不同，标志版面大小各异，常需针对性的进行结构受力、挠度、基础倾覆和滑移稳定等验算。计算时需要几个结构、基础计算软件交叉使用，操作比较繁琐，而且由于其真实计算过程被封闭在黑箱中，使用者只能被动接受运算结果，不便于检查过程。设计工作是基于规范的条文和公式进行的，仅仅依靠最终计算结果是不行的，计算纸式的工作仍然需要。对此，部分设计人员采用Word编写计算稿、Excel来进行计算。由于Excel的公式编制过程中需要选择大量单元格，直观性较差，公式填写过程中若出现问题，一般较难发现，计算结果容易出错。MathCAD的出现，很好地解决了这一问题。

MathCAD是美国PTC公司推出的一个功能很强的数学软件。它集数理计算、图形和文字处理等功能于一体，能方便直观的解决数学问题和数学在各种学科中的应用问题。MathCAD把Excel的自动计算和Word的所见即所得界面结合起来，可按照规范和工程约定的符号编写公式，其过程完全可见。编写出的计算书和设计人员手写的计算书具有相同的风格，计算过程一目了然，校对计算书的人可以完全不懂MathCAD——只需要有工程专业知识。借助该软件，专业设计人员可把精力集中到设计问题的本质上，提高思维质量和工作效率。

2 交通标志支撑结构的设计[1-3]

交通标志支撑结构设计主要包括横梁和立柱钢管的形变、强度计算，连接节点计算、基础稳定性计算等内容。其中强度和稳定性设计已有相应的标准，而挠度计算基于杆件的形状，会有所不同的，以下主要针对挠度计算进行详细分析。

钢管的挠度采用梁的挠曲线近似微分方程进行计算：

式中：M（x）——梁的弯矩方程；

E——材料弹性模量；

I（x）——截面惯性矩方程。

当用于支撑指路标志、交通诱导牌等大型标志牌、因为悬挑距离短、荷载大，受力均匀，一般采用等截面杆件，其惯性矩为常量，式（1）可改写成

对于集中荷载、分布荷载等受力情况通过查相关材料力学书籍即可得到相应的挠度、转角计算公式。

当杆件较长时，比如信号灯杆、车道指示标志杆横梁悬挑都在8 m以上。钢管的受力分布曲线是从端部到根部由小增大，若使用等截面杆，则变得不经济，在满足根部强度要求时，端部强度富余量偏高，同时因杆件材料用量增加，自重提升加大了挠度控制的难度，因此这类标志杆多采用正多边形变截面杆件。

变截面杆件的EI由于沿长度变化，其挠曲方程较为复杂，通过目前工程中计算多采用如分段总和法近似求解，而该计算法存在分段少则误差大，分段多计算步骤繁冗计算量大的问题。本次利用MathCAD的符号计算功能通过对式（1）积分直接获得正多边形变截面杆件挠曲公式。

以L型单悬臂标志杆横梁为例，横梁在标志板风荷载作用下发生水平位移，其任意截面所受弯矩如下：

式中：P——标志板风荷载；

L——横梁长度。

钢管截面惯性矩

式中：λ=(R0-Rd)/L——截面变化率；

R0——横梁根部半径；

Rd——横梁端部半径；

t——壁厚；

k——截面形状系数，跟正多边形边数有关，见表1。

表1 截面系数

因为钢管属于薄壁结构，截面惯性矩可简化为：

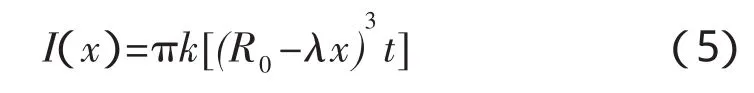
将式（3）和式（5）代入式（1），整理后，微分方程如下：

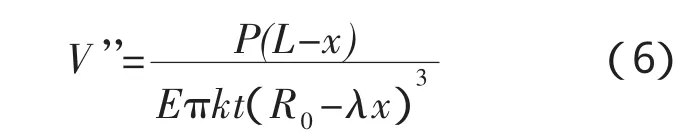
利用MathCAD的符号运算功能，进行积分运算得到转角和挠度公式：

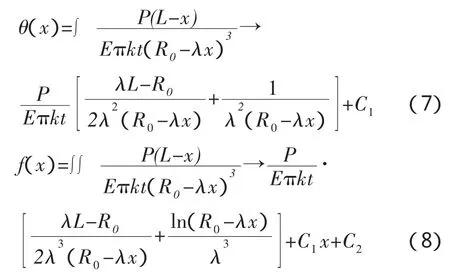
式中：C1,C2——积分常数。

积分常数C1,C2、可由边界条件θ(0)=0和f（0）=0联立求解得到，自此获得正多边形变截面横梁的标志板风荷载作用下的转角和挠度解析式。

同样的，由横梁自重、标志板自重、横梁风载导致的横梁挠曲变形均可按以上步骤求得对应的解析式。

3 应用示例

下面是基于上述推导结果的MathCAD应用示例。在编写好的计算书中仅需输入少量的初始参数，即可实时自动计算，根据设置的条件自动判断是否满足挠度要求。

（1）输入数据

标志板参数：板长a=1 m，宽b=1.2 m，数量n1=6，板中对中间距1.7 m，板厚 t1=3 mm，材料密度ρ=2.85 gm/cm-3；横梁参数：变截面八棱柱体杆件，根部半径为R0=140 mm，端部半径为Rd=75 mm，壁厚 t2=7 mm，材料密度 ρ=7.85 gm/cm-3，长度L=11；风荷载参数：风速 V=31 m/s。

（2）自动计算各标志板作用下的挠度结果

标志牌自身荷载作用f1=12.42×103m

横梁自身荷载作用f2=64.13×103m

标志牌风荷载作用f3=110×103m

横梁风荷载作用f3=10×103m

（3）结构优化

对于定长横梁，其挠度与Rd、R0、t负相关，而用钢量与 Rd、R0、t正相关，因此可以通过给 Rd、R0、t采用值域赋值，可自动计算一系列挠度和用钢量，并利用MathCAD的绘图形功能绘制截面尺寸与挠度的关系图，从中选取优值。以Rd为例，取值范围50～90 mm，得到各尺寸的挠度和用钢量，见表2和图1。

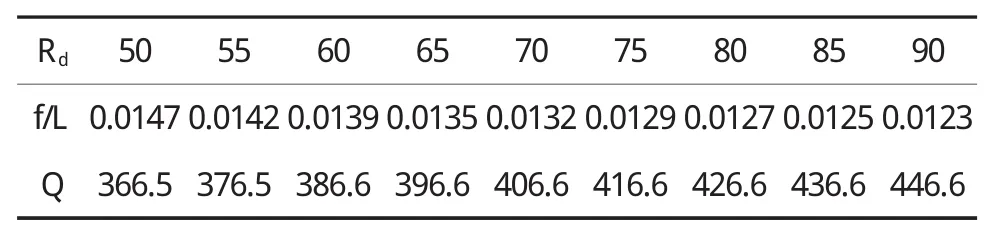
表2 挠度和用钢量

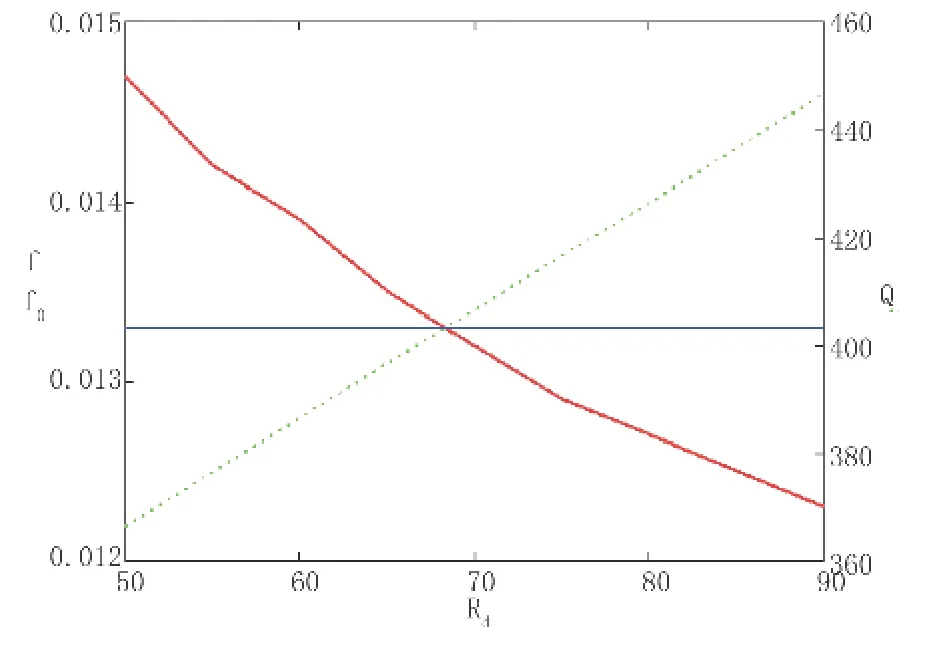
图1 挠度与用钢量图

根据图表可知，挠度满足要求时，Rd取70 mm即可。

4 结语

上述示例仅是交通标志杆件设计中的一部分，根据初始段数据的输入，所有计算、中间数据的传递均自动执行，最终得到标志杆的强度、变形、螺栓连接、基础等一系列结果，大大简化了交通标志杆件结构设计中的人工计算工作。其输出与手写格式一样的计算书，设计人员可以看到计算的整个过程，从而可以放心的为计算结果负责。当规范或要求有变化时，还可以迅速修改既有模板以适应新的需求。可以说MathCAD是适合设计人员的优秀工程计算工具。

[1]殷惠光,张正威.变截面构件的挠度计算[J].连云港职业大学学报,1998(4):44-47.

[2]赵峰,李成玉.输电钢管塔杆的挠度计算[J].武汉工业大学学报,1999(2):53-55.

[3]钱陪翔.关于建筑力学的两个命题[J].山西建筑,2001(6):17-18.