基于拓扑优化的桥梁结构选型
2015-01-09玉海珑
玉海珑,李 伟
(天津城建设计院有限公司,天津市 300121)
1 拓扑优化的概念
一座选型优秀的桥梁应该是结构合理,传力明确,富于力感,给人一种稳定的感觉。在一些常见的结构中,为了节省材料,通常会去除对整体受力贡献很小的部分,例如路灯杆的柱脚加劲板(见图1),通常不是矩形,而是对矩形钢板外侧角进行倒角处理,这样即节省了材料用量,同时也让整个构造显得更具稳定性。总结众多颇具力感与稳定性的建筑可以发现,构件的体量及线性在受力不同的部位是有着细致的区分的,以圣地亚哥·卡拉特拉瓦设计的密尔沃基美术馆为例,正式这种细致的区分赋予了建筑强大的张力,见图2。多余的用料会破坏结构整体的力感,罗伯特·马亚尔在设计萨尔基纳山谷桥(见图3)的过程中就是通过对石膏模型的研究,去除了实腹拱桥中对承受荷载贡献较小且破坏桥梁整体力感的冗余部分,该桥的设计得到了众多桥梁设计师的广泛认可,被评为世界最美桥梁第一名[1]。
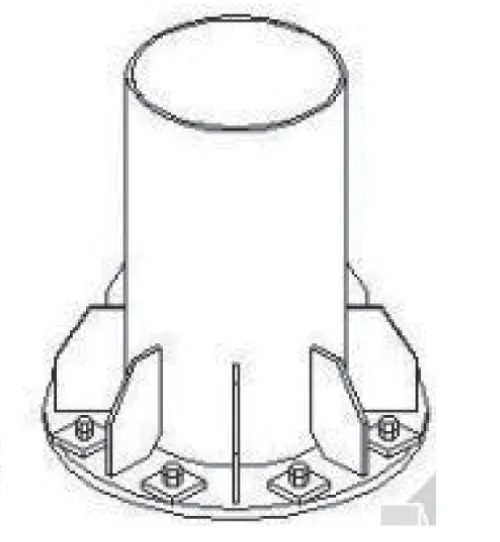
图1 柱脚加劲板

图2 密尔沃基美术馆局部

图3 萨尔基纳山谷桥
同时,一座选型优秀的桥梁还应当具有很好的整体性和连续性。桥梁结构的连续性主要表现在构件交接处线型“渐变”的体形特征上。当结构构件处突然变换方向时,会出现应力集中现象,从视觉上也会破坏桥梁造型的连续性。从力学及美学的观点看,构件的交接以光滑曲线的过渡是比较理想的,此时应力分布更加均匀,力流通过更加顺畅。例如20世纪世界最美桥梁排名第4名的德国克希汉姆跨线桥(见图4,施莱希设计),梁体采用和弯矩图一致的流线造型,桥梁力感十足,在整体性和连续性方面堪称典范。

图4 德国克希汉姆跨线桥
可以发现,材料的优化使用,和造型的力感营造在一定程度上是相得益彰的,因为材料的优化使得力流传递途径得以凸显,这种材料的优化使用方式称作拓扑优化,其目的就是在单独荷载或多个荷载的作用下,寻求对材料的最佳使用方式,即造型的优化[2]。
2 拓扑优化方法的适用条件
在现有桥梁结构中这种通过造型优化来凸显力感的案例并不是非常多,因为体现力流传递的流线造型通常会带来设计施工难度的加大,所以在常规桥梁的设计中通常会简化处理,例如小跨径的板梁、小箱梁等预制结构通常都采用等截面设计,保证荷载作用最强的截面满足受力及使用要求即可。
对于跨径较大,并一定景观要求的桥梁,在设计中使用拓扑优化可以提升景观效果、优化结构受力、有效节省材料,图5所示斜腿刚构桥,主梁采用了等截面的设计方式,与德国克希汉姆跨线桥相比,设计施工难度有所降低,但明显造成了材料的浪费和造型的呆板。

图5 某斜腿刚构桥
对于大跨径的拱桥、悬索桥和斜拉桥,由于主梁高度相对桥梁跨径较小,且主梁受力较为均匀,不适宜用拓扑优化方法进行处理,在拱肋、主塔及局部构造的选型过程中可采用拓扑优化方法。
3 拓扑优化的原理
根据圣维南原理,分布于弹性体上一小块面积或体积内的荷载所引起的物体中的应力,在离荷载作用区稍远的地方,基本上只同荷载的合力和合力矩有关,荷载的具体分布只影响荷载作用区附近的应力分布。
而国内在进行结构设计或弹性阶段分析时,为了简化计算模型,通常会引入平截面假定和胡克定律,认为垂直于杆件轴线的各平截面(即杆的横截面)在杆件受拉伸、压缩或纯弯曲而变形后仍然为平面,并且同变形后的杆件轴线垂直且固体材料受力之后,材料中的应力与应变(单位变形量)之间成线性关系。如图6所示,引入两大假定后,可拓扑优化的区域就被忽略掉了,这样设计出的结构体现出的力流传递和实际情况有一定的出入,所以不论从材料用量和力感营造上都是较差的[3]。
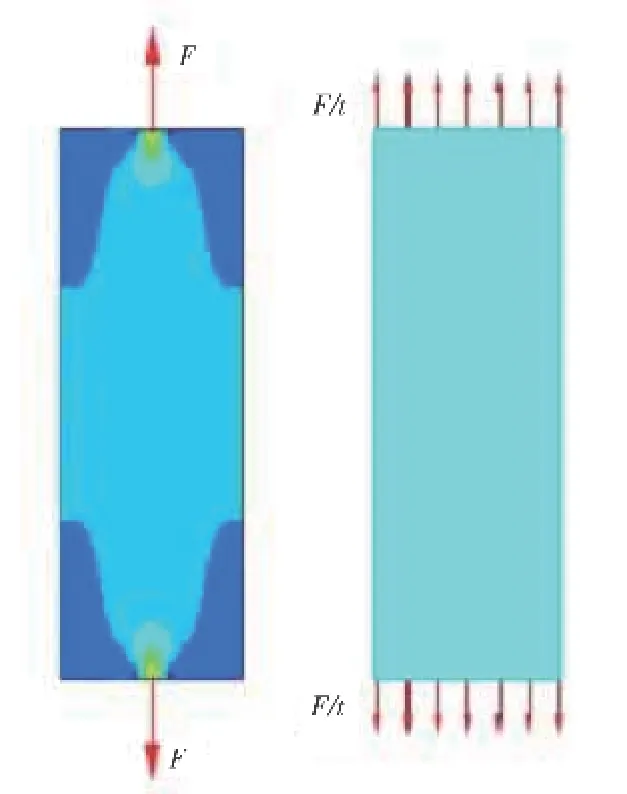
图6 圣维南原理与平截面假定
美国的AASHTO规范已经将这一问题考虑到设计中,引入了D区构件的概念,认为钢筋混凝土D区构件是一类截面应变不符合平截面假定的构件,其受力比较复杂,梁截面理论已不再适用。在钢筋混凝土结构的设计中,D区的配筋是需要优化设计的。通过这种方法,节省了钢筋材料的用量,而在施工复杂性(主要是模板制作安装)和混凝土材料优化的博弈中还是选择了前者。但是D区设计理念对实现桥梁结构拓扑优化还是具有一定的指导意义[4]。
有限元法是一种相对比较成熟的分析方法,假想的把一连续体分割成数目有限的小体(单元),彼此间只在数目有限的指定点(节点)相互连结,组成一个单元的集合体以代替原来的连续体,再在节点上引进等效力以代替实际作用于单元上的外力。选择一个简单的函数来近似地表示位移分量的分布规律,建立位移和节点力之间的关系。

有限元法的实质是:把有无限个自由度的连续体,理想化为只有有限个自由度的单元集合体,使问题简化为适合于数值解法的结构型问题。
从理论上讲,拓扑优化寻求的是最小挖空率下最小化结构变形能,并以此为目标函数。程序对每个单元赋予一个内部伪密度,伪密度为0表示该处材料将被去掉,伪密度为1表示该处材料将被保留。如图7所示,通过数值解法可得到杆件的受力情况,继而可得到区域的伪密度,达到优化目标的杆件将会被去掉,最终得到优化后的结构外形。
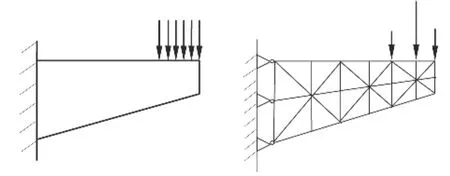
图7 采用有限元法对结构进行离散
4 案例分析
根据拓扑优化原理,可采用有限元分析软件Ansys进行拓扑优化分析,主要分为以下步骤:定义拓扑优化问题;选择单元类型和材料属性;建立模型,并制定优化和不优化的区域;定义和控制荷载工况;定义和控制优化过程;查看结果。
以某双支点桥墩为例进行拓扑优化分析,命令流结构如下:


图8(a)为仅考虑支座竖向力的单工况下材料优化20%的结果,和圣维南原理所述吻合;图8(b)为同时考虑墩顶双向水平力的三工况下材料优化40%的结果,通过该图,在没有进行其他分析计算的情况下,也可以了解墩高较高、水平力作用相对较强的情况下桥墩的设计思路。如图9所示中安康汉江桥斜撑体量较竖直桥墩体量小,但对于提升结构整体稳定性的作用却更大,在桥梁的整体造型中也更具力感。
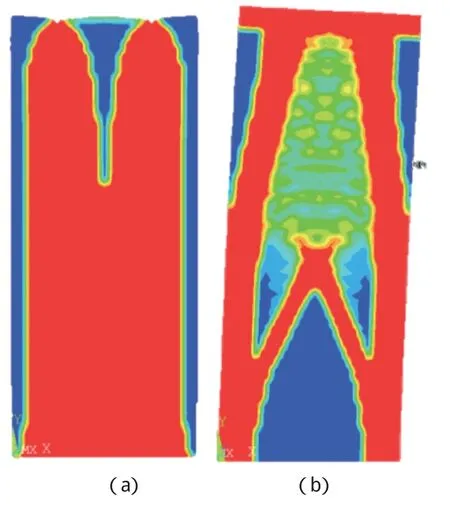
图8 双支点桥墩拓扑优化结果

9 安康汉江桥
[1]江苏省交通规划设计院有限公司.桥梁概念设计[M].北京:人民交通出版社出版,2010.
[2]项海帆.桥梁概念设计[M].北京:人民交通出版社出版,2011.
[3]陈艾荣,盛勇,钱锋.桥梁造型[M].北京:人民交通出版社,2005.
[4]AASHTO LRFD Bridge Design Specifications[M].The American Association of State Highway and Transportation Officials,2004.
