基于离散变量优化的航天器质量特性配平方法

郭璠 田娜 陈向东 张正峰

（北京空间飞行器总体设计部，北京 100094）

1 引言

质量特性配平设计是航天器总体设计的关键环节之一，减少配平使用配重的质量能够有效减少航天器整器质量。航天器为降低姿态控制的难度，提高控制的准确性，须进行质量特性配平工作，即通过在航天器结构上安装一定量的配重，将航天器的质量、质心、转动惯量或惯性积调配到一定的目标范围内。由于受运载火箭推力的限制，质量一直是航天器设计中重要的约束条件之一。随着航天器系统愈加复杂，质量呈现不断增长的趋势，减重迫在眉睫；而减少配平使用的配重安装量是航天器减重的重要途径之一［1］。

航天器质量特性配平存在两个难点：一是耦合性，受航天器构形布局的约束，预留的配重安装位置有限，且可能呈现既不均匀又不对称的状态，将导致X、Y、Z 三个方向质心（或转动惯量）在配平时发生耦合，即每一块配重都会同时影响航天器质心（或转动惯量）的三个方向坐标；二是离散性，配平使用的配重块一般预先加工，配平时采用多个配重块组合安装完成，因此可使用的配重质量离散。

目前，传统的航天器质量特性配平方法仍通过多次的质量特性测试［2］与配平计算相结合确定。但由于耦合性和离散性问题，测试须凭经验，通过修正配重安装位置及质量逐方向、反复修正三个坐标值才能使质心逼近目标值，而每次修正都不可避免地带来配平计算、配重实施及测量的工作量，不但耗时耗力，而且修正过程中的配重质量很可能逐步增加，给航天器减重工作带来困难。

最优化方法是一种能够有效解决配平优化的方法，国内已有相关研究［3-6］，但均有不足。文献［3］通过Insight-fd优化软件解决了配平的耦合性问题，但不能解决离散性问题；文献［4］通过查表法解决了配平耦合性和离散性问题，但需要穷举所有配重块组合安装的形式，复杂航天器配平计算的工作量很大，不能解决实际问题。

本文为解决质量特性配平的耦合性和离散性两个难点，提出一种利用序列二次规划＋分支定界的离散变量优化方法寻求配平设计的最优解，介绍了优化函数建立过程和离散变量优化方法原理及实现，并通过实际算例表明该方法可直接获得质量最优的配平方案，较传统方法大大降低了配重质量及安装时间，可获得最优的配平布局及配重质量，有效避免了重复配平的操作，提高了总装配平工作的效率（本文的质量特性仅指质量和质心，转动惯量可以按照类似的方式计算）。

2 配平优化初始条件分析

在解决航天器质心配平问题之前，应明确如下条件，作为配平问题优化的初始条件。所有位置参数均在同一参考坐标系下给出。

（1）航天器进行配平前，需完成了一次初始的质量特性测试，获取配平前整器质量Mo，质心在整器坐标系下的位置向量Po＝［xo，yo，zo］T，其中xo，yo，zo分别为质心在整器坐标系下的三个坐标分量。

（2）航天器进行总装设计的过程中，会在结构上预留多处配重安装位置，同时设计与配重安装孔相匹配的配重块，备选配重块质量一般有多种选择，典型的配重安装方式如图1所示，以下参数在配平前已知：①配重点在整器坐标系下的位置向量Pi＝［xi，yi，zi］T（i＝1，2，…，l），其 中xi，yi，zi分别为配重点在整器坐标系下的三个坐标分量，i为配重点序列，配重点共l个；②备选配重质量mz，z 为配重块序列，z ＝1，2，…，n，种类数n 一般通过人为预先确定；③同一配重点安装的配重块的线密度DA，DA＝mZ／d，d 为 配 重 块 厚 度；④隔 热 垫 厚 度dt；⑤配重安装用紧固件套数（i＝1，2，…，l）和单套紧固件质量ms，设ms为常量（常用紧固件M5钛合金内六角螺钉，60mm 与20mm 两种长度规格质量差仅2.6g，可忽略）。

图1 典型航天器配重安装形式Fig.1 Typical installation form of balance mass on spacecraft

对配重点i，可得该点配重质量Mi和质心位置向量：

（3）配重安装质量一般有上限不超过Mst，即0≤Mi≤Mst。

3 配平优化问题构建

有约束最优化方法的思想是通过探索变量值，在同时满足不等式和等式约束的条件下使目标函数取得最小值。优化问题的一般形式为

式中：a为不等式约束函数的个数，b为等式约束函数的个数。

质心配平优化目标为安装配重的总质量最小，优化约束一般有如下几种形式：

（2）Y 方向质心位置Py不大于ry；

（3）Z 方向质心位置Pz不大于rz。

综上，可建立质心位置配平优化问题的优化函数：

式中：Q 为优化变量集合，表示在各配重点每种配重块个数的集合，共有n×l个独立分量，所有变量均为整数；Px，Py，Pz为配重安装后航天器质心坐标：

4 优化方法选择

若假设式（5）的优化变量Q 中的所有分量均可取实数，则式（5）为一个典型的非线性约束最优化问题，常用序列二次规划法（Sequential Quadratic Programming，SQP）求解。

4.1 序列二次规划法

SQP法是求解非线性最优化问题的一类有效算法［7］，具有超线性收敛速度。SQP法通过拉格朗日函数将原有约束问题转化为无约束问题：

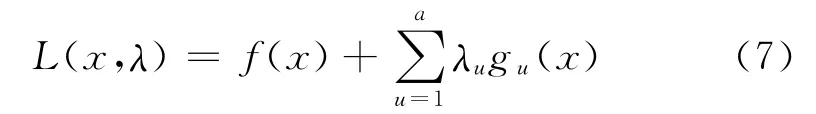
式中：x 为优化变量；gu（x）为优化约束函数；λ 为约束函数加权因子。

利用拟牛顿法来近似构造Hessian矩阵，建立二次规划子问题：

式中：d ＝x-x（k）；Hk＝∇2L（x（k），λ（k）），为式（8）的Hessian矩阵［8］。

对于给定初始值（x（k），Hk）（k＝0），求解式（8）求得其目标函数在x（k）处的一个下降方向dk并进行一维搜索，求得迭代步长αk；而后采用BFGS修正，使Hk＋1保持正定；令x（k＋1）＝x（k）＋αkdk，k＝k＋1，持续迭代计算，直至dk＝0，得出最优解。

4.2 序列二次规划与分支定界的离散变量优化方法

当Q 可取实数时，利用SQP法易求得每个配重点的最优配质量。但实际情况中，配重块个数必须为整数，直接运用SQP 法求得最优Q 值往往是小数，如对结果直接进行圆整，将很可能偏离最优解。

分支定界法是求解整数规划常用的一种方法，其核心思想是对有约束条件的所有可行解空间进行搜索，把全部可行的解空间不断分割为越来越小的子集（称为分支），并为每个子集内的解计算一个上界（称为定界）。在每次分支后，对凡是界限超出已知可行解值的那些子集不再做进一步分支（称为剪枝），许多子集就可以不予考虑，从而缩小了搜索范围。

本文将分支定界法与SQP 法相结合使用求解符合整数约束条件的最优解，利用SQP求解优化变量的实数解，同时利用分支定界法缩小求解空间，直至SQP法求得的最优解为整数。算法流程如下：

（1）SQP 求解：忽略整数约束条件，利用SQP法将原问题按连续变量问题求最优解，如果最优解其中至少有一个变量为非整数q（i），明确其整数部分和小数部分：

（2）分支：构造2个子问题，在原目标函数和约束条件的基础上，一个问题增加约束，另一个问题增加约束

（3）定界与剪枝：通过不断分支与求解各个子问题来不断修正上界完成定界。上界由已经得到的可能最优整数解（子问题中符合整数条件的目标函数值最小者）确定。通过将不可能存在最优解的子问题舍弃完成剪枝。求解每个子问题时会出现以下几种情况：①子问题无可行解，则此问题不需继续分支，该子问题被剪枝；②得到一个整数解，则此问题不需继续分支，该子问题被剪枝。若该整数解在目前得到的所有整数解中最优，则将其定为新的上界；③得到一个非整数解，若该子问题目标函数值大于等于已得到的上界时，则该子问题被剪枝，否则继续向下分支。

（4）重复步骤①、②、③，对产生的每个子问题不断分支并求解由分支产生的新子问题，直至求得一个近似整数解为止。

利用MATLAB软件为平台，本文开发了质心配平设计优化程序，整个算法的流程见图2。

图2 算法实现流程Fig.2 Flow chart of the algorithm

5 配平计算实例

某航天器总装设计中要求进行横向质心配平，配平要求见表1，配重布局见图3，备选配重、紧固件等参数见表2。

表1 某航天器质量特性及配平目标Table 1 Mass properties of a spacecraft and target of mass balancing

图3 某航天器可选配重点布局示意图Fig.3 Optional potision of balance mass on a spacecraft

测试人员进行3次尝试配平，最终配平设计方案详见表3和图4，运用本文优化方法，经1次优化运算（计算时间514.3s）的配平设计方案详见表4，获得的配重布局如图5所示（图中黑色实点代表安 装紧固件位置）。

表2 某航天器配平设计约束条件Table 2 Restriction of mass properties balancing

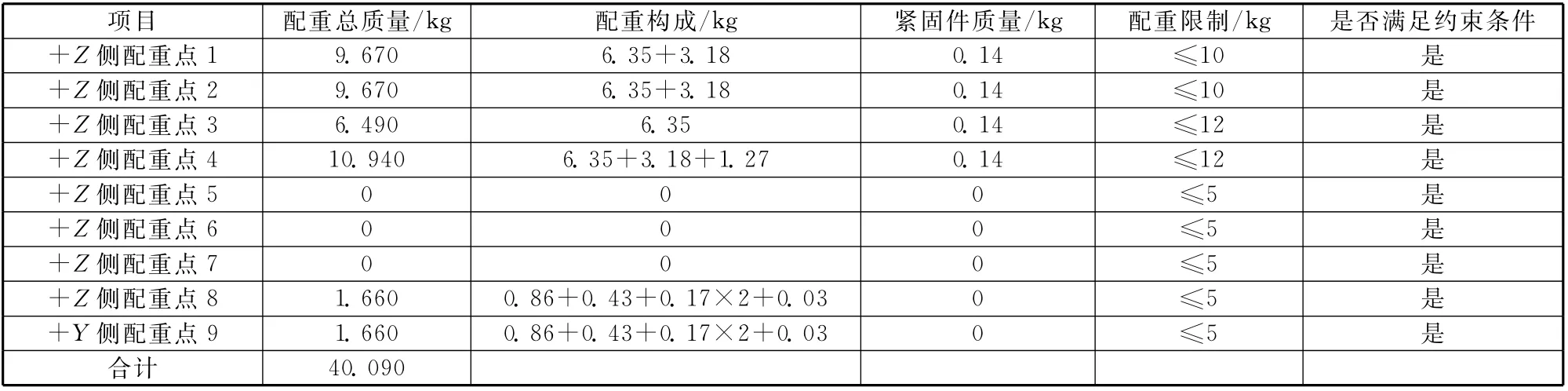
表3 使用传统配平方法获得的配重方案Table 3 Scheme of mass balancing using traditional method

图4 传统配平方法配重布局Fig.4 Distribution of balance mass using traditional method

表4 本文提出的配平方法获得的配重方案Table 4 Scheme of mass balancing using discrete variables optimization

对两种方法的结果进行对比，详见表5，可知利用本文算法进行配平方案设计可直接获得最终配平方案，配平不需进行多次尝试，且在满足横向质心配平目标的同时，配重总质量较人工配平减小了3.62kg，表明优化后的配平方案设计更为合理。

图5 本文配平方法配重布局（＋Z 侧板配重布局）Fig.5 Distribution of balance mass using discrete variables optimization

表5 两种方案结果比较Table 5 Contrast of two schemes

6 结论

本文运用最优化方法，建立了质心位置配平的目标函数，提出了利用一种序列二次规划＋分支定界的离散变量优化方法获得配重设计方案的最优可行解，本文方法较目前传统质量特性配平方法有如下优势：

（1）根据配平目标仅需经过一次优化计算，即可获得最优配重设计方案，与传统配平方法需逐方向进行配平相比，能够解决配平耦合性问题，同时大大降低采用传统配平方法需多次进行配平计算、配重调整、质量特性测试的工作量，避免了重复配平实施带来的总装风险；

（2）考虑了配平过程中配重块和紧固件的质量呈离散性的实际因素，优化结果可直接用于实际工程应用；

（3）可适用于多种质量特性配平相关的约束条件，例如单个配重质量，配重总质量，配重点位置，配平质心范围，转动惯量、惯性积等，可完成诸如质心、转动惯量、甚至惯性积的配平；

（4）提高了航天器配平工作的效率，缩短了航天器的研制周期。

（References）

［1］张旺军，陈向东，潘艳华，等.一种航天器电缆网精确质量特性计算方法［J］.航天器工程，2014，23（4）：33-38 Zhang Wangjun，Chen Xiangdong，Pan Yanhua，et al.A method of accurate mass property calculation for spacecraft cable network［J］.Spacecraft Engineering，2014，23（4）：33-38（in Chinese）

［2］陈勉，杜晨.卫星质心三轴快速测量配重新工艺［J］.航天器环境工程，2005，22（6）：358-360 Chen Mian，Du Chen.New technology of fast measuring satellite 3axis centre of mass［J］.Spacecraft Environment Engineering，2005，22（6）：358-360（in Chinese）

［3］尹航，高永明，董正宏，等.基于虚拟样机技术的航天器配重设计与实现［J］.系统仿真学报，2010，（11）：2631-2634 Yin Hang，Gao Yongming，Dong Zhenghong，et al.De-sign and implementation of spacecraft balance based on virtual prototype technology［J］.Journal of System Simulation，2010，（11）：（in Chinese）

［4］侯文，郑宾，杨瑞峰.鱼雷质心配重纠偏技术的实现［J］.测试技术学报，2003，17（1）：52-55 Hou Wen，Zheng Bin，Yang Ruifeng.Correction of torpedo’s centroid eccentricity with counterweight technology［J］.Journal of Test and Measurement Technology，2003，17（1）：52-55（in Chinese）

［5］侯悦民，季林红，金德闻.小卫星动平衡灵敏度分析［J］.中国空间科学技术，2003，23（3）：27-34 Hou Yuemin，Ji Linhong，Jin Dewen.Sensitivity analysis of the dynamic balancing of small satellites［J］.Chinese Space Science and Technology，2003，23（3）：27-34（in Chinese）

［6］William E L.Triaxial balancing techniques（A study of spacecraft balance with respect to multiple axes）［R］.Washington D.C.：NASA，1964

［7］茨木俊秀.最优化方法［M］.北京：世界图书出版公司，1997 Ibaraki T.Optimization methods［M］.Beijing：World Publishing Corporation，1997

［8］Powell M J D.A fast algorithm for nonlinearly constrained optimization calculations［J］.Numerical Analysis，1978，630：144-157