数学软件在研究生数学建模实验中的应用
2015-01-08杨云峰曾昭英赵提财
杜 辉 杨云峰 曾昭英 赵提财
(1.东北石油大学数学与统计学院,黑龙江 大庆163000;2.东北石油大学研究生院,黑龙江 大庆 163000)
在科技高速发展的今天,高精尖人才的培养是其强有力的后盾。而研究生阶段就是培养高精尖技术型人才的重要阶段。创新能力的培养是研究生阶段培养的重要能力之一。数学建模课程就是培养研究生创新实践能力的重要课程。只有理论是不够的,很多理论都是在实践的基础上得以应用和延伸,所以研究生数学建模实验就变得非常重要了。
既然是实验,就离不开计算机编程。计算机编程就离不开数学软件。在东北石油大学研究生数学建模实验中,主要应用的数学软件有Matlab、Lingo、R等软件,这些软件的学习与使用将理论与实际紧密的联系在了一起。本文将举例一些东北石油大学研究生数学建模实验实例,并应用相应的数学软件进行求解。
1 Matlab软件在数学建模实验中的应用
例1 一年生植物春季发芽,夏季开花,秋季产种,有一部分种子可以活过冬天,其中的一部分能在第二年春季发芽,然后开花、产种,剩下的种子虽然未发芽,但如果又能活过第二年冬天,则其中的一部分还能在第三年春季发芽,然后开花、产种,如此继续,一年生植物只能活一年,假设种子最多能活过两个冬天,建立数学模型研究该植物的数量变化规律,以及它能一直繁殖下去的条件。
1.1 符号引入
xk——该一年生植物在第k年的数量;
c——每棵植物秋季产种的平均数,c>0;
a1——一岁的种子能在春季发芽的比例,0<a1<1;
a2——两岁的种子能在春季发芽的比例,0<a2<1;
b0——零岁的种子能活过冬天的比例,0<b0<1;
b1——一岁的种子能活过冬天的比例,0<b1<1;
b——种子能活过一个冬天的比例,0<b<1;
1.2 模型假设
假设 a1>a2;b0=b1=b;a1,a2,b,c 均为常数。
1.3 模型建立和求解
根据模型假设,列式得
x1=a1bcx0(1)
xk=a1bcxk-1+a2b(1-a1)bcxk-2,k=2,3… (2)
令 p=a1bc (3)
q=a2(1-a1)b2c (4)
(1)和(2)可以改写为
x1=px0(5)
xk=pxk-1+qxk-2,k=2,3… (6)
由二阶常系数线性齐次差分方程解法可得(3.6)的解为

通过分析可知一年生植物能一直繁殖下去的充分必要条件是
Matlab程序:
a1=0.5;a2=0.25;c=10;
bs=2/(sqrt(a1.*c).^2+4.*a2.*(1-a1).*c)+a1.*c);
b=bs+bs.*[.01,0,-.01]
p=a1.*c.*b;q=a2.*(1-a1).*c.*b.^2;
x=[100,100,100];x(2,:)=p.*x(1,:);n=20;
for k=2:n;
x(k+1,:)=p.*x(k,:)+q.*x(k-1,:);
disp(‘在b>b*,b=b*,b<b*三种情况下一年生植物数量的演变’);
disp(‘年 b>b*b=b*b<b*’);
disp[(0:n)’,round(x)];
命令窗口显示的计算结果为
bs=0.19089 b=0.1928 0.19089 0.18898
结果分析:(1)当b>b*时,一年生植物数量将无限增长;
(2)当b=b*时,一年生植物数量将趋于稳定值;
(3)当b<b*时,一年生植物将濒于灭绝。
2 R软件在数学建模实验中的应用

把(3)、(4)代入(8)得

则一年生植物能一直繁殖下去的充分必要条件是
b*≤b<1
1.4 Matlab 求解
取 a1=0.5,a2=0.25,c=10,由(10)计算临界值 b*,然后取 x0=100,分别在b>b*,b=b*和b<b*三种不同情况下用循环语句计算一年生植物的数量在20年内的演变过程。
例2假定某电池厂宣称该厂生产的某种型号电池寿命的中位数为140A.h.为了检验该厂生产的电池是否符合其规定的标准,现从新近生产的一批电池中抽取20个随机样本,并对这20个电池的寿命进行了测试,其结果如下(单位:A.h):
137.0 140.0 138.3 139.0 144.3 139.1 141.7 137.3 133.5 138.2
141.1 139.2 136.5 136.5 135.6 138.0 140.9 140.6 136.3 134.1
试用Wilcoxon符号秩检验分析该厂生产的电池是否符合其标准。
R程序:
>X<-scan()
1:137.0 140.0 138.3 139.0 144.3 139.1 141.7 137.3 133.5 138.2
11:141.1 139.2 136.5 136.5 135.6 138.0 140.9 140.6 136.3 134.1
21:
Read 20 items
>Wilcox.test(X,mu=140,alternative= ”less”,exact=FALSE,correct=FALSE,conf.int=TRUE)
Wilcoxon signed rank test
data:X
V=34,p-value=0.00703
Alternative hypothesis:true mu is less than 140
95 percent confidence interval:
-Inf 139.2000
Sample estimates:
(pseudo)median
138.2000
结果分析:这里 V=34 是 Wilcoxon 统计量,P 值 0.007034<0.05,拒绝原假设,即中位数达不到140A.h.
3 Lingo在数学建模实验中的应用
例3 分配甲、乙、丙、丁、戊去完成A,B,C,D,E五项任务,每人完成一项,每项任务只能由一个人去完成,五个人分别完成各项任务所需时间如下表所示,试作出任务分配使总时间最少。
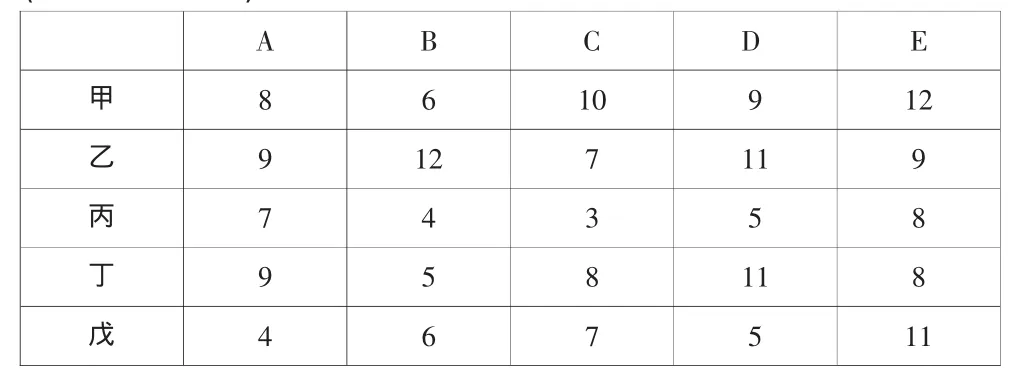
表1
Lingo程序如下:
MODEL:
SETS:
WORKER/W1.W5/;
JOB/J1.J5/;
LINKS(WORKER,JOB):C,X;
ENDSETS
DATA:
C=

表2
ENDDATA
MIN=@SUM(LINKS:C*X);
@for(WORKER(I):@SUM(JOB(J):X(I,J))=1);
@for(JOB(J):@SUM(WORKER(I):X(I,J))=1);
@for(LINKS:@BIN(X));
END
求解得到五个变量x11,x25,x33,x42,x54等于1,其他变量等于0,代表甲完成任务A,乙完成任务E,以此类推。目标函数值为30。
4 结论
本文列举了将Matlab、R、Lingo应用于数学建模中的实例。数学建模实验不仅让学生们学到了很多课上学不到的东西,扩展了自身的理论知识,提高了计算机编程水平,同时也使得理论与应用紧密的结合在一起,理论得以实现。如何选择合适的教学模式,选择合适的实验题目将是今后研究的一个方向。
[1]章绍辉,编.数学建模[M].北京:科学出版社,2010.
[2]薛毅,陈立萍,编.R 统计建模与 R 软件[M].北京:清华大学出版社,2014.
[3]袁新生,邵大宏,郁时炼,编.LINGO 和 EXCEL在数学建模中的应用[M].北京:科学出版社,2007.
