复杂结构井井下工具通过能力分析

张 琴 张慢来 周志宏 谢丽芳

（长江大学机械工程学院，湖北 荆州 434023）

0 引言

井下工具可顺利穿过井筒是开展井下作业的前提[1-3]。随着我国钻采技术的不断发展，大斜度定向井开发日益普遍，井身结构越来越复杂[4]，对相关工具结构尺寸的要求亦更加严格，有必要进一步分析不同曲率井眼下的工具通过能力，为工具设计提供有用参考。

1 井眼曲率半径确定

图1 三维井眼的几何关萦

增量为

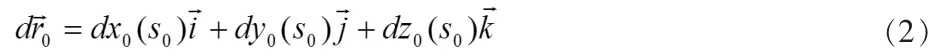
过点O井眼轴线的切线单位矢量在xpy平面上的投影为τ→0，它与之间的夹角是井斜角φ，与i→之间的夹角为方位角ψ。根据图1，有

式中，s0为井眼轴线的曲线坐标；分别为沿 x、y、z 坐标轴的单位矢量。

井眼轨迹曲线的曲率定义为

将式（4）代入（5）并化简，得

假设井身测量点有N个，则井眼轨迹有N+1段。设第i段相邻测量点间的测深增量为Δs，方位角增量为Δψ，井斜角增量为Δφ，则该段曲率为：

式中，Ki为第i段的曲率，rad/m；φi为第i个测斜段的井斜角，rad。

曲率半径为Ri=。

2 允许工具通过的最大长度

可顺利下入的井下工具最大长度受井眼轨迹、井筒尺寸及工具直径的影响。井下工具的可下入性要求工具的总长度小于井筒允许通过的最大长度L。如图2所示，考虑工具在弯曲、造斜段发生的变形，按以下方法确定工具的通过能力。

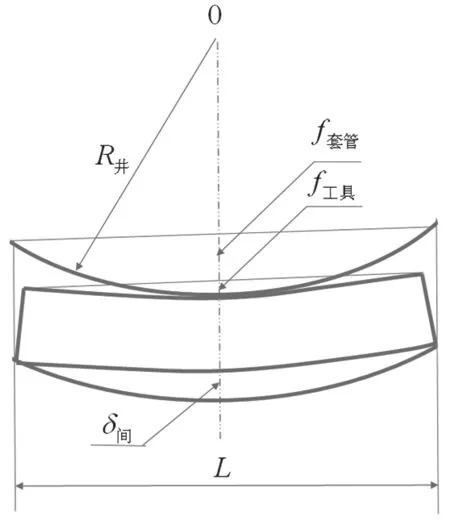
图2 井下工具通过能力的几何示意图

则 δ间=()×1000

所以，允许工具通过的最大长度L(m)根据下式确定，即

式中：R井为井眼轨迹的最小曲率半径，R井=min(R1、R2、R3、…、RN+1)，m；k井是井眼轨迹的最大曲率rad/m；k工具为工具允许的变形曲率，rad/m；δ间为工具与井壁的最大间隙，mm。

当工具为刚体，则不考虑变形时，k工具=0，有

对于整体组合和钻具，其变形受到严格限制，建议按式12计算工具的最大通过能力。另外，还可以根据式13设计在给定工具结构参数下的最小井眼曲率半径。

3 井下工具通过能力分析

在刚性条件下，工具通过能力L仅与井眼（套管）直径、工具外径及井眼曲率有关，对于不同的套管—整体锻造工作筒尺寸：（1）套管直径222mm，工作筒外径168mm、总长2250mm；（2）套管直径150.4mm，工作筒外径140mm、总长2066mm，根据式12计算的工作筒最大允许长度随井眼狗腿度的变化规律如图3所示。

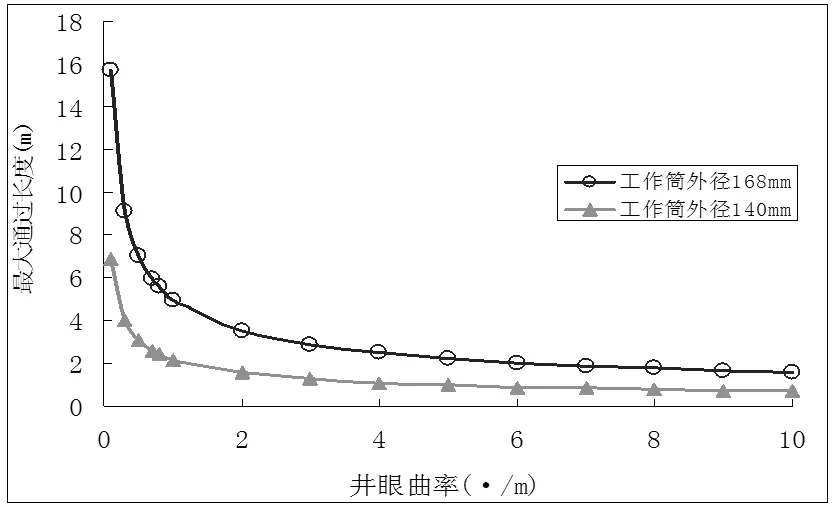
图3 最大允许通过长度随井眼曲率的变化

要保证以上总长分别为2250mm、2066mm的工作筒能够顺利入井，设计井眼曲率应分别小于4.848o/m、1.117o/m。

对应两种不同直径、长度的工作筒，若井眼的设计曲率分别取4.848o/m、1.117o/m，要使工作筒能够顺利入井，可增大井眼（套管）直径。工作筒最大允许通过长度随井眼（套管）直径的变化如图4所示。由图可看出，随着井眼直径的增大，工作筒的最大允许通过长度不断增大。

图4 最大允许通过长度随井眼（套管）直径的变化

4 结束语

本文通过建立描绘空间井眼轨迹的数学表达式，推导出井眼曲率半径公式，得到允许工具通过的最大长度，进一步分析了工具长度、直径随井眼曲率的变化，为施工工艺的设计提供科学依据。

［1］刘巨保,罗敏,邹野,等.φ139.7套管内侧钻水平井弯螺杆钻具通过能力分析[J].钻采工艺,2003,26(1):15-16.

［2］沈曦,张强,陈灿,等.大位移井磨铣打捞管柱可下入性分析[J].机械工程师,2008,12:31-32.

［3］甘庆明,杨承宗,黄伟,等.大斜度井井下工具通过能力分析[J].石油矿场机械,2008,37(7):59-61.

［4］罗井泉,蔡俊杰,周建生,等.大斜度井举升泵下入通过性计算[J].河南石油,2002,16(2):40-42.