套管缺陷交流阻抗检测与定位方法研究

吴银川，张家田，严正国，苏 娟

(西安石油大学光电油气测井与检测教育部重点实验室，陕西西安710065)

金属套管主要用于钻井过程以及完井后对井壁的支撑，以保证整个油井的正常运行。在老井中，金属套管长期处于井下高温、高压、强腐蚀的环境中，套管本身会出现孔洞、裂缝、扭曲变形、腐蚀、断裂等缺陷。这些缺陷对油井安全以及生产测井造成严重的影响。为及时了解油井套管的动态缺陷信息，需对套管缺陷特征进行识别，并定量检测套管缺陷，以方便对套管使用情况作动态的评估。目前常见的金属管筒缺陷无损电检测方法有:漏磁法［1］、涡流法［2-3］以及直流电阻抗法［4-5］。漏磁法利用强磁场将套管磁化，当金属材料存在缺陷时，磁通分布会发生变化，利用霍尔效应测量材料的磁通密度，根据其变化来检测材料缺陷;涡流法根据电磁感应原理，利用发射线圈产生交变的电磁场，在材料内部产生涡流，当材料存在缺陷时，电流分布会发生变化，通过测量远端接收线圈中的二次感应电动势的大小及相移来检测材料的缺陷。漏磁法采用阵列传感器可判断缺陷在厚度方向的位置，涡流法通过阵列发射多种频率信号，阵列接收响应信号可判断缺陷在厚度方向的位置，但是漏磁法和涡流法在仪器设计以及结果解释方面相对复杂。直流电阻抗法通过给材料注入直流电流，测量一定距离上的电压，根据欧姆定理定量计算被测段的阻抗，估计被测段的缺陷情况，检测结果解释简单，易于成像。但直流电阻抗法无法对缺陷在厚度方向上定位，实际仪器直流漂移与测量信号均为直流信号，且数量级相近，给后续信号检测带来影响。为此，本文根据趋肤效应提出了利用交流阻抗测量原理进行缺陷检测和定位。在交变场中，趋肤效应影响电磁波在金属导体中的传播，进而影响金属导体的交流阻抗，对于规则导体(如圆柱体)可采用理论计算公式进行阻抗定量计算［6-7］，当导体存在不规则缺陷时理论计算十分困难。论文采用多物理场耦合软件(COMSOL)建立有限长金属套管三维模型，通过仿真得到理想套管、缺陷套管的电场和电位的分布曲线，分析了曲线分布规律。仿真实验结果表明:根据缺陷套管阻抗变化率，能检测出金属套管的内、外壁缺陷，通过改变频率，能实现外壁缺陷的径向定位。该方法也可用于其他金属导体缺陷检测和定位。

1 电磁场理论

1.1 趋肤效应

金属套管(良导体)具有高的电导率和大的传导电流。由于欧姆损耗是连续存在的，电磁波所携带的能量会随着波在金属套管中传播而不断衰减。金属导体材料中，损耗角正切σ/(ωε')≫1，电磁波的传播常数［8］

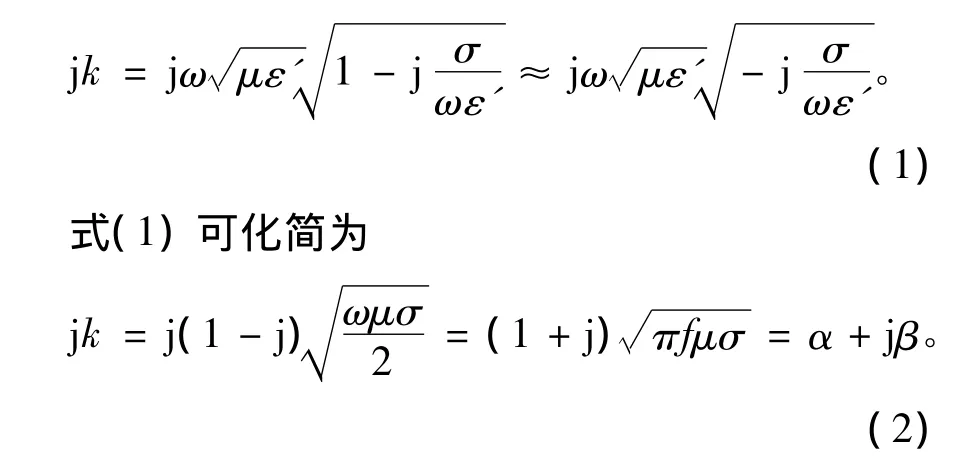
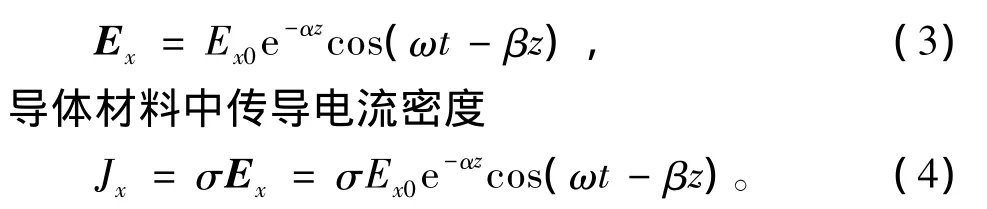
式(3)和(4)中传导电流密度和电场强度随着透入导体深度的增加而呈指数衰减，该现象称为趋肤效应。趋肤效应是影响过套管电磁测井的主要因素之一。在z=1/α =1/β 处衰减到e—1=0.368 倍，令δ=1/α表示这个距离，称为趋肤深度。趋肤深度是描述电磁波在导体传播的一个重要参数。趋肤深度的大小与电磁波的频率、导体电导率以及磁导率有关。当z方向距离为3δ时，电场(电流密度)衰减到e—3≈0.05倍，此时工程上可近似认为电磁波全部衰减。采用趋肤深度δ重写式(3)有

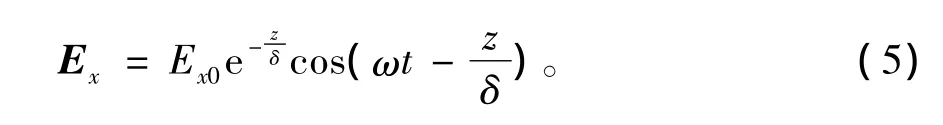
1.2 功率计算

电磁场中电场Ex与磁场Hy之间有如下关系:

其中η称为波阻抗。在电介质中波阻抗

其中ω为电磁波频率，μ为材料磁导率，σ为材料电导率，ε'为材料介电常数。由于良导体满足 σ≫ωε'，因此式(7)可化简为

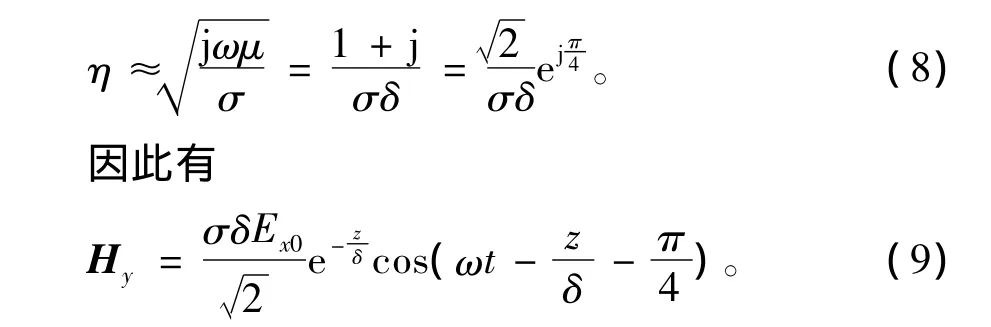
比较式(5)和式(9)可知，在导体中，沿 +z方向传播的电磁波电场强度在相位上超前磁场强度π/4。电场和磁场的向量形式:

复坡印亭矢量Pz的实部为有功功率的密度值，该值表示能量的流动，体现导体的电阻性;虚部是无功功率的密度，该值表示电磁能量的交换，体现导体的电感性。式(13)显示，在一个透入深度δ的距离内，功率密度衰减为表面值的e—2=0.135倍。

2 缺陷测试方法

2.1 电流分布

如图1所示，设金属套管的长度为L，套管内壁注入电流环和回流环之间的距离为l，注入电流为IS。由于趋肤效应的影响，电流趋于金属套管的内外壁表面。一部分电流I0从注入电流环开始沿套管内壁流入回流环;另一部分电流I1从电流环开始沿套管内壁，通过套管端面，流经整个套管外壁，最后回到套管内壁的回流环。

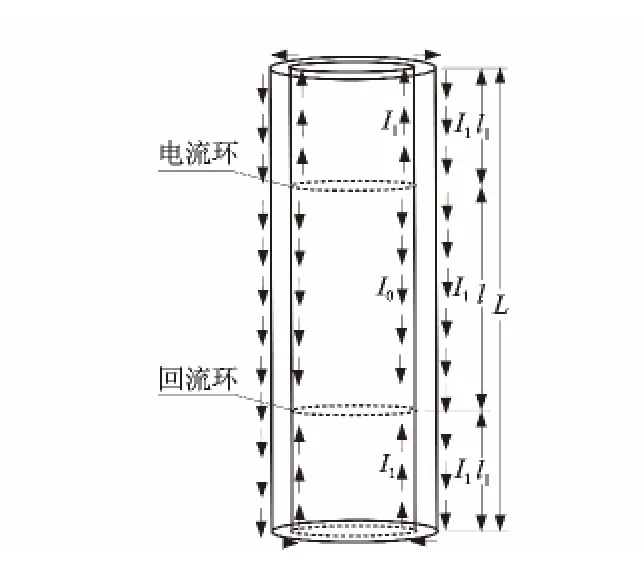
图1 金属套管电流分布Fig.1 Current distribution in metal casing

2.2 等效电路

金属套管等效电路如图2所示，Z0表示电流环和回流环之间的内壁等效阻抗;Z1表示电流环与套管上顶端之间的内壁等效阻抗，由于对称性，同样接地环与下顶端之间的内壁等效阻抗也为Z1;Z2表示顶端等效阻抗;Z3表示外壁等效阻抗。

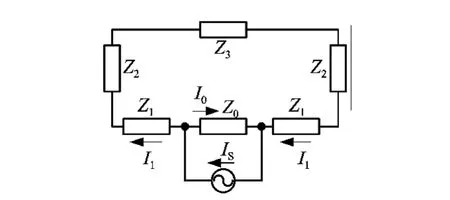
图2 金属套管等效电路Fig.2 Equivalent circuit of metal casing

在正弦稳态条件下，根据电路定律，各电流之间满足:

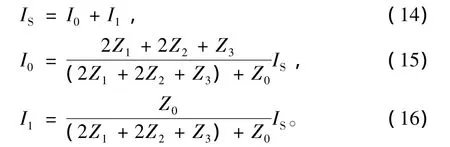
图1所示金属套管中，在电流环与回流环之间的距离l确定后，当套管整体长度L≫l时，此时阻抗Z0≪ (2Z1+2Z2+Z3)，即有:

当套管整体长度为有限长时，I1的分流不可忽略。在实际套管井中，套管长度达数千米，因此式(17)成立。

2.3 套管缺陷测试方法

通过检测套管阻抗值大小实现缺陷检测与定位。如图1所示，在套管井内l目标段，通过电流环向金属套管内壁注入电流，电流沿套管流回回流环，通过检测目标段内一定距离阻抗(或电压)值来判断被测段套管是否存在缺陷;在同一检测位置，改变注入电流频率，通过阻抗(或电压)值可判断金属套管在厚度(径向)方向是否存在缺陷。具体缺陷检测步骤为:第一步，根据待测金属套管的参数(电导率σ和磁导率μ)计算激励频率和趋肤深度δ关系，确定套管检测厚度3δ;第二步，根据套管厚度Δa与3δ的关系，计算注入电流的频率f值;第三步，检测无缺陷金属套管(如井口套管)在不同频率点下阻抗的大小;第四步，信号频率从低到高依次进行，对目标段套管进行阻抗检测;第五步，比较第三步和第四步阻抗检测值，当检测阻抗值与无缺陷套管阻抗值相同时，可以确定在离套管内壁3δ范围内无缺陷，否则在离套管内壁3δ范围内有缺陷存在。

3 套管仿真模型

3.1 理想套管模型

理想金属套管模型如图3所示，其中套管内半径为a，套管厚度为Δa，长度为L，目标段长度为l3。电流环和回流环紧贴套管内壁，环宽度为l2。为简化仿真计算模型，这里选取有限长套管作为研究对象。在有限长套管内，分流电流I1不可忽略，但对于确定套管来说，忽略该值不会影响阻抗的相对变化规律。这里选取L=60 cm，a=7 cm，Δa=2 cm，l2=1 cm，l1=14 cm，l=30 cm，l3=10 cm，选取套管电导率σ =4×106S/m，相对磁导率μr=100，相对介电常数εr=1。利用多物理场耦合软件COMSOL建立该三维模型，套管外为理想绝缘介质，选取电场和磁场类型，进行频域稳态分析。

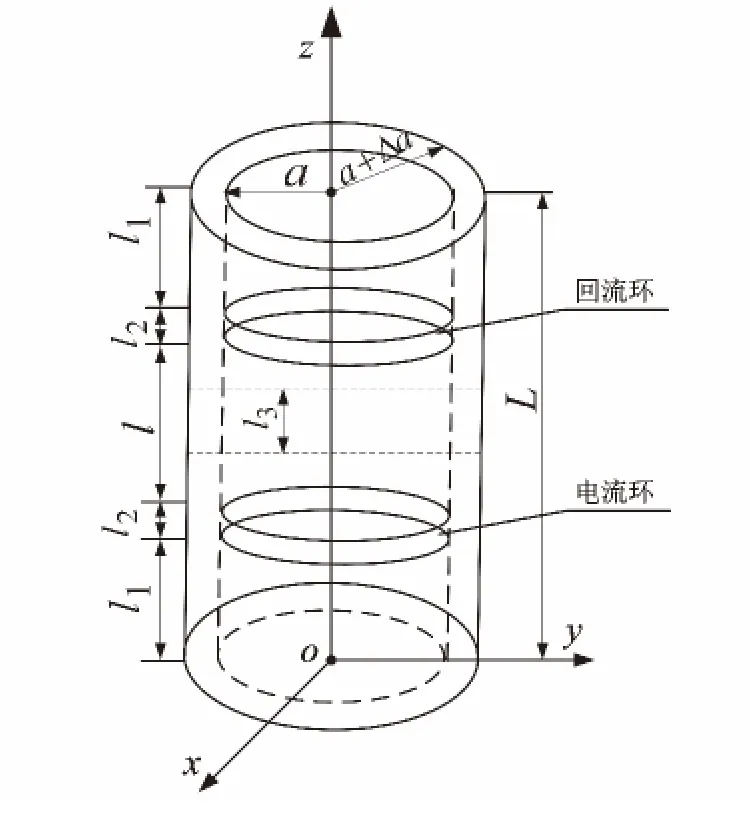
图3 理想套管模型Fig.3 Model for ideal casing

3.2 均匀腐蚀模型

为验证2.3节所提出的缺陷测试方法，建立均匀腐蚀套管模型。图4所示为内壁均匀腐蚀模型，在l3目标段，内壁均匀腐蚀0.5 cm，其他参数不变;图5所示为外壁均匀腐蚀模型，在l3目标段，外壁均匀腐蚀0.5 cm，其他参数不变。

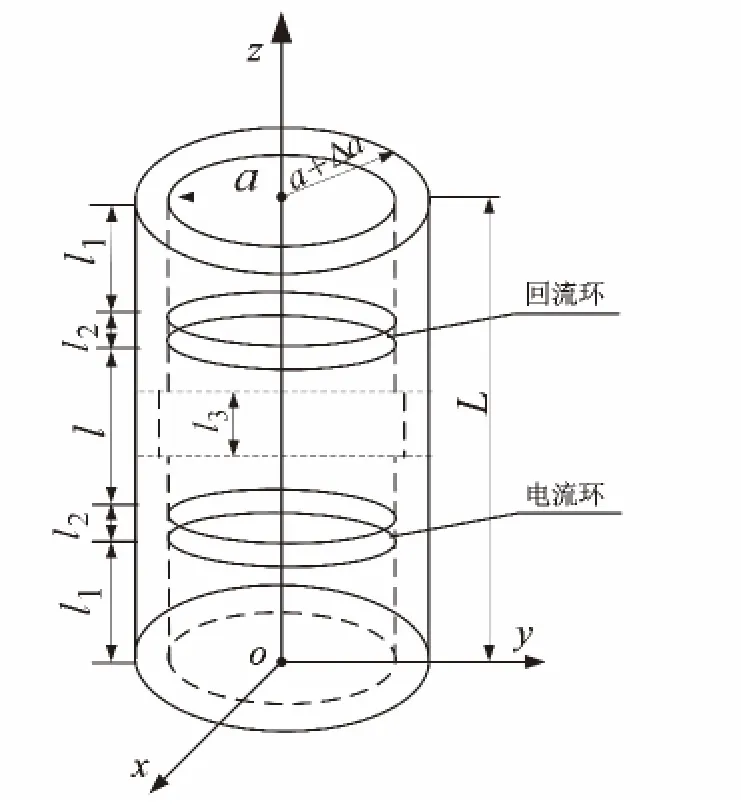
图4 内壁均匀腐蚀套管模型Fig.4 Model for the casing uniformly corroded in inner wall

图5 外壁均匀腐蚀套管模型Fig.5 Model for the casing uniformly corroded in outer wall

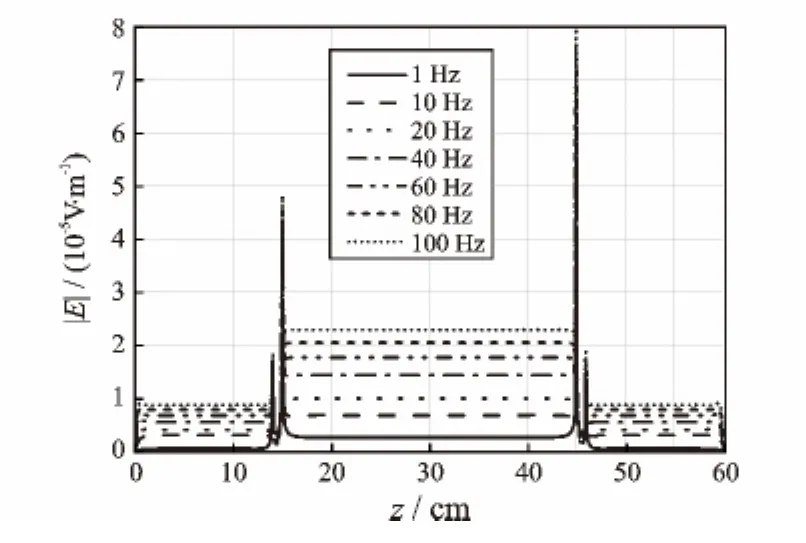
图6 理想套管轴向电场分布(x=7 cm，y=0 cm，z=0～60 cm)Fig.6 Electric field distribution of ideal casing along axial line(x=7 cm，y=0 cm，z=0～60 cm)

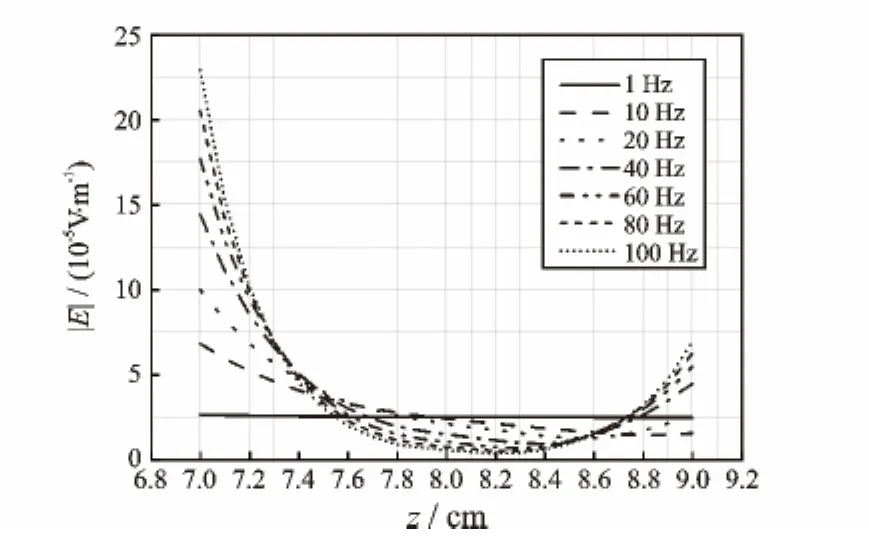
图7 理想套管径向电场分布(z=30 cm，y=0 cm，x=7～9 cm)Fig.7 Electric field distribution of ideal casing in radial direction(z=30 cm，y=0 cm，x=7～9 cm)

3.3 网格剖分

由于金属套管比较薄，交流电注入套管将产生趋肤效应，电流趋于套管内外表面，因此在金属套管内外表面附近剖分网格要密。软件自动网格剖分不合理，不能满足精度要求，从而导致计算不收敛的情况，因此采用手动剖分。具体剖分策略:由电流环和回流环出发实现渐变剖分，由套管内外表面向套管内实现由密到疏剖分。套管模型满足轴对称，因此先在纵向二维平面(zox或zoy)上实现面剖分，然后利用软件扫掠功能实现整体剖分。

4 仿真实验结果

4.1 电场分布

理想套管轴向电场分布如图6所示，在电流环和回流环之间(z=15～60 cm)电场分布均匀;在电流环(z=14～15 cm)和回流环(z=45～46 cm)附近由于源存在电场出现跳变;在其余各段(z=0～14 cm，z=46～60 cm)电场均匀。总体来说，频率越高电场强度越大;频率相同时，电流环和回流环之间的电场强度大于其他段。理想套管径向电场分布如图7所示，在套管内壁(x=7 cm)和外壁(x=9 cm)处电场强度大，极小值出现在套管内部;频率越高电场强度越大，其电场分布曲线变化率越大;频率降至1 Hz时，在套管径向电场变化率最小，此时可近似认为电场在该频率条件下分布均匀，趋肤效应现象消失。内壁腐蚀套管电场分布如图8所示，频率越高，电场越大;除1 Hz外，同频率下腐蚀段(z=25～35 cm)电场低于无腐蚀段电场。外壁腐蚀套管电场分布如图9所示，频率越低腐蚀段电场变化越大，频率越高腐蚀段电场变化越不明显。

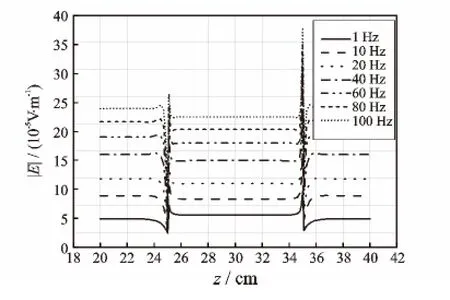
图8 内壁腐蚀套管轴向电场分布(x=7 cm，y=0 cm，z=20～40 cm)Fig.8 Electric field distribution of inner wall corrosion casing along axial line(x=7 cm，y=0 cm，z=20～40 cm)

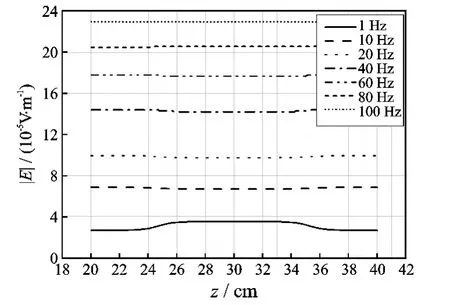
图9 外壁腐蚀套管轴向电场分布(x=7 cm，y=0 cm，z=26～34 cm)Fig.9 Electric field distribution of outer wall corrosion casing along axial line(x=7 cm，y=0 cm，z=26～34 cm)

在正常段选择z=20 cm点，腐蚀段选择z=30 cm点为观测点，定量研究电场的变化情况，具体数值如表1和表2所示，其中表示z=20 cm的电场表示z=30 cm的电场，ΔrE表示电场相对变化率，计算公式为:

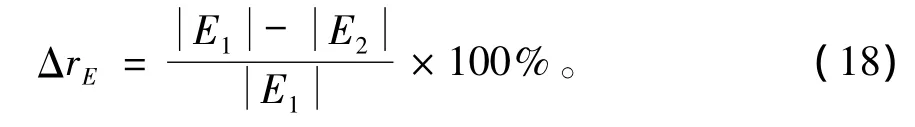
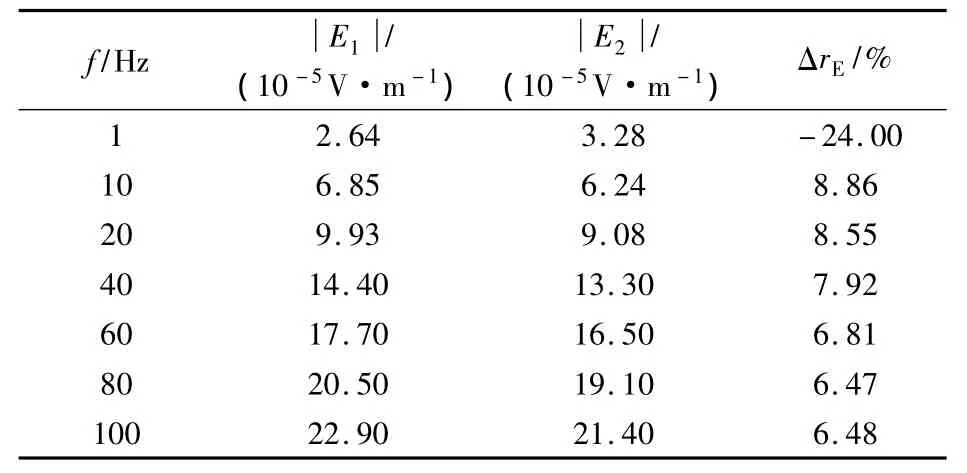
表1 内壁腐蚀套管电场参数Tab.1 Electric field parameters of inner wall corrosion casing

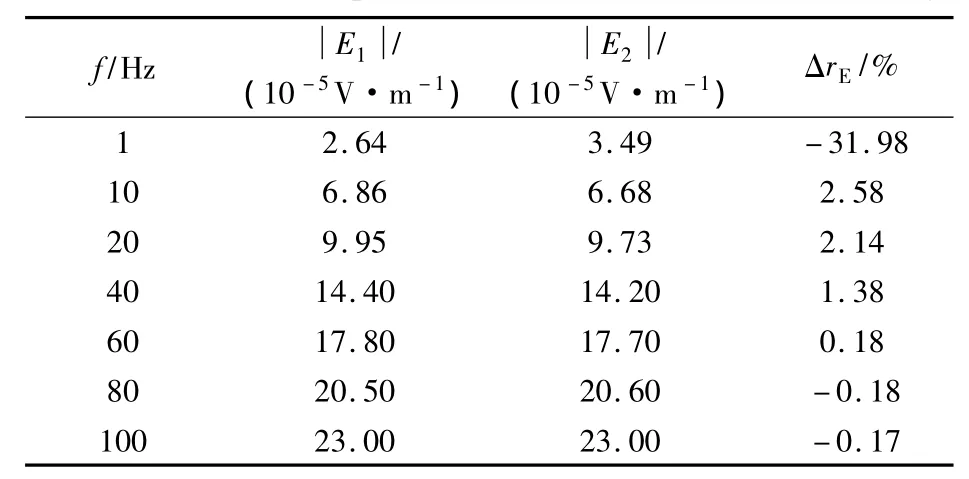
表2 外壁腐蚀套管电场参数Tab.2 Electric field parameters of outer wall corrosion casing

如表1所示，当套管内壁腐蚀时，除1 Hz外，腐蚀段与正常段相比电场均变小，而1 Hz时腐蚀段电场变大，1 Hz时电场变化率最大，为 —24.00%。如表2所示，当套管外壁腐蚀时，频率越低电场变化越明显，1 Hz时电场变化率为 —31.98%，100 Hz时电场变化率为 —0.17%。

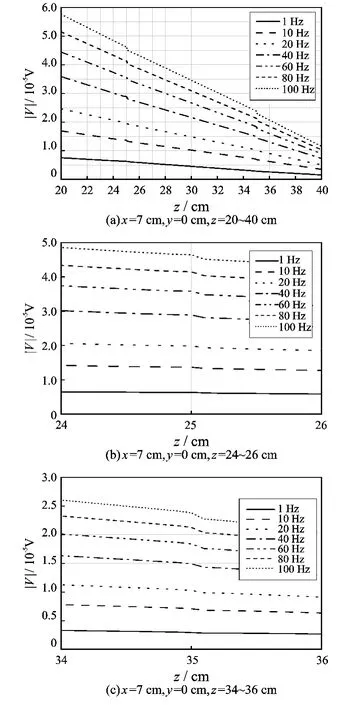
图10 内壁腐蚀套管电位分布Fig.10 Potential distribution along the axial line of inner wall corrosion casing

4.2 电位分布

内壁腐蚀套管电位分布如图10所示，由于趋肤效应影响，当电流大小相同时，频率越高电位越大;内壁存在腐蚀时，各频率下电位曲线斜率在腐蚀边界处(z=25 cm和z=35 cm)附近发生明显变化。如图10(b)和(c)所示，在腐蚀边界处电位快速下降，频率越高，变化越明显。因此通过电位连续测量曲线可辨识出腐蚀段(z=25～35 cm)，电位线突变处即是腐蚀段的边界处，当电位分布曲线具有图10所示特征变化规律时，可以判断套管内壁存在腐蚀。

外壁腐蚀套管电位如图11所示，由于内趋肤效应的影响，随着电流频率变高，电流越集中于套管内壁表面，因此频率越高，外壁腐蚀对电位影响越小;频率越低，外壁腐蚀对电位影响越大。因此，在腐蚀段(z=25～35 cm)和腐蚀边界处(z=25 cm和z=35 cm)，频率越高电位曲线变化越不明显，通过电位曲线变化特点可以确定套管内壁无缺陷，缺陷位于套管外壁。

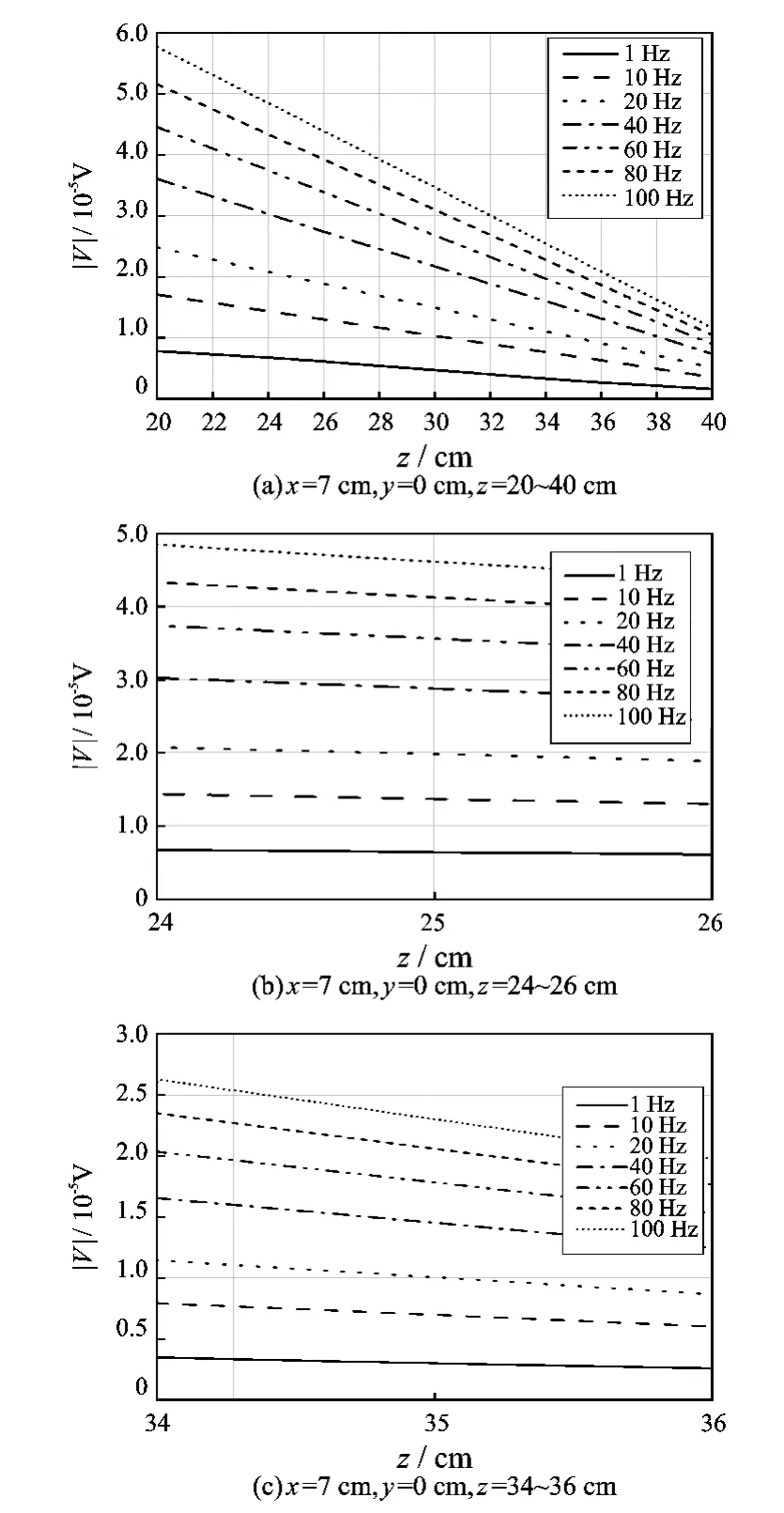
图11 外壁腐蚀套管电位线分布Fig.11 Potential distribution along the axial line of outer wall corrosion casing

4.3 阻抗计算

4.3.1 趋肤深度的计算 根据以上分析，趋肤深度δ与频率f、磁导率μ以及导体电导率σ有关，仿真实验选取金属套管参数如3.1节所述，在各频率下趋肤深度δ的值如表3所示。

表3 趋肤深度计算数值Tab.3 Calculation values of skin depth

4.3.2 均匀腐蚀仿真计算 根据欧姆定律计算阻抗:

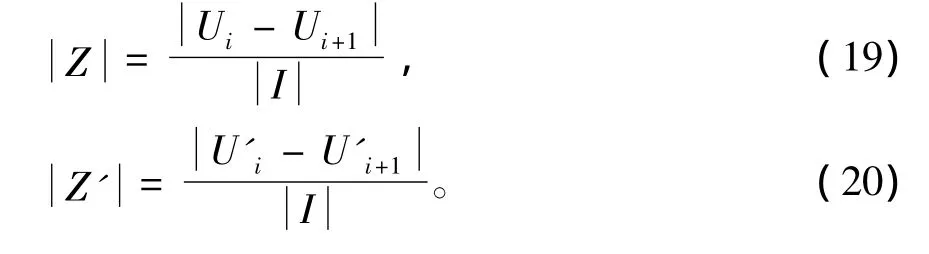
其中Ui和Ui+1分别表示无缺陷段确定距离点上电位值，U'i和U'i+1分别表示被测段相同距离点上电位值，I表示流过套管电流值。实际检测时可根据检测段阻抗与无缺陷段阻抗的相对变化率ΔrZ来判断缺陷的情况:

利用COMSOL软件建立图5和图6所示均匀腐蚀模型，仿真计算数据如表4和表5所示。正常段选取z=20～25 cm段套管，检测段选取z=27.5～32.5 cm段套管。如表4所示，内部均匀腐蚀0.5 cm时，在各频率点上，检测段阻抗和正常段阻抗相比均发生变化。由表3知，1 Hz时趋肤深度δ=25.15 mm，趋肤深度δ大于套管本身厚度(Δa=20 mm)，可以近似认为，在此频率下电流密度均匀分布在套管横截面上，此时检测的阻抗值是套管的整体阻抗;对1 Hz来说，缺陷套管有效横截面积变小，因此检测缺陷阻抗值大于正常段套管阻抗值。与正常段套管相比，高频条件下，缺陷段电流密度作用横截面积将变大，因此测得缺陷段阻抗值比正常段阻抗值要小。通过表4可以得到具体结论:1 Hz时，与正常段相比，检测段阻抗变大，阻抗变化率36.58%，表明整体来说检测段套管存在缺陷;频率大于1 Hz，检测段阻抗均小于正常段阻抗，阻抗变化率在 —3.97% ～ —5.24% 之间，表明目标段套管在内壁存在缺陷，结合1 Hz时的结果，可确定目标段套管内壁存在腐蚀。

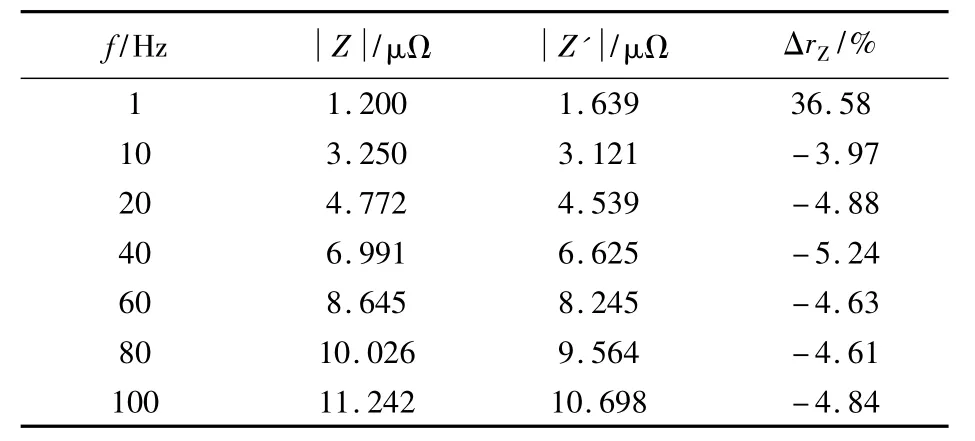
表4 内均匀腐蚀套管阻抗计算Tab.4 Impedance of inner wall corrosion casing

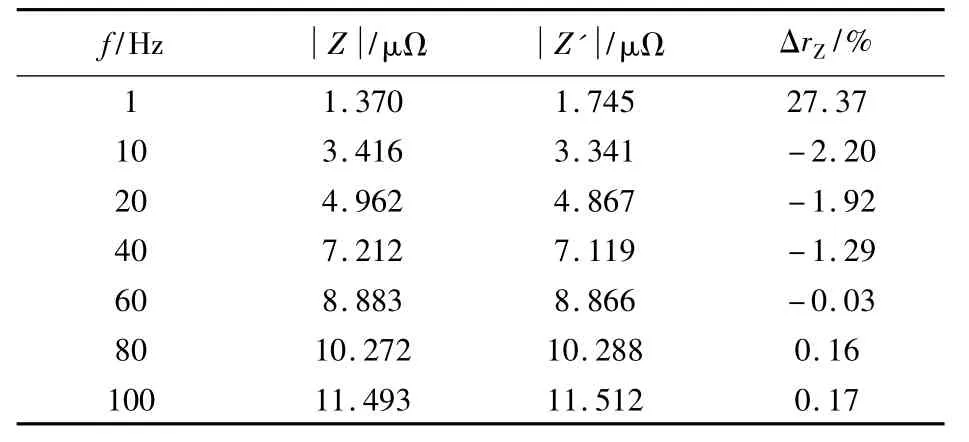
表5 外均匀腐蚀套管阻抗计算Tab.5 Impedance of outer wall corrosion casing

当套管外壁存在缺陷时，如表5所示，随着频率的增加，检测段和正常段阻抗趋于相同。和表4相同，在1 Hz时缺陷套管段横截面积变小，因此检测缺陷阻抗值大于正常段套管阻抗值。随着频率的增加，趋肤深度δ变小，电流密度趋于套管内壁，外部均匀腐蚀对阻抗测量的影响变小。如表5中所示，在频率为60 Hz时，阻抗变化率下降到0.03%，此时可以认为检测段阻抗与正常段阻抗相同。通过表5数据可得到具体结论:1 Hz时，与正常套管相比，检测段阻抗变大，变化率为27.37%，表明检测段套管存在腐蚀;随着频率的增加，检测段阻抗趋于和正常段阻抗相同，若以阻抗变化率的0.1%作为界限，在频率大于60 Hz时，检测段阻抗和正常段阻抗相同，可以认为在离内壁9.75 mm范围内套管无腐蚀，该腐蚀位于离内壁9.75 mm之外，该结论与给定外均匀腐蚀模型结论一致，因此该方法能有效检测外壁腐蚀，并能确定腐蚀在套管径向方向的位置。

5 结论

(1)趋肤效应影响金属套管交流阻抗值，与正常无缺陷套管相比较，在不同频率条件下缺陷套管阻抗将发生变化。

(2)套管内壁存在腐蚀时，随着电流频率增大，缺陷段套管交流阻抗相对变化率趋于常量;除超低频率(可近似认为是直流)外，缺陷段阻抗值均小于正常段阻抗;通过该阻抗值变化规律可确定套管内壁存在缺陷。

(3)套管外壁存在腐蚀时，随着电流频率增大，缺陷段套管交流阻抗相对变化率趋于零;电流频率较高检测段阻抗值等于正常段阻抗;通过该阻抗值变化规律可确定套管外壁存在缺陷;根据趋肤深度可进一步在径向方向上定位缺陷的具体位置。

(4)直流(或超低频)阻抗法能检测出被测段是否存在缺陷，但是缺陷在套管外壁还是在内壁难以确定，而交流阻抗法可进一步判断出缺陷的径向位置。

［1］ 付西光，颜国正，左建勇，等.漏磁法智能管道壁厚检测系统的研究［J］.仪器仪表学报，2004，25(6):799-801.

［2］ 陈文明，何辅云，陈琨，等.石油管道检测中缺陷类型判别方法的研究［J］.合肥工业大学学报:自然科学版，2008，31(12):1929-1932.

［3］ 吴相楠，李陇杰，张冰，等.基于电涡流传感器的金属材料表面形貌三维可视化检测［J］.传感技术学报，2012，25(3):370-373.

WU Xiang-nan，LI Long-jie，ZHANG Bing，et al.3D visually detection of surface topography of metal material using eddy current sensors［J］.Chinese Journal of Sensors and Actuators，2012，25(3):370-373.

［4］ 张静，解社娟，陈振茂.泡沫金属直流电位法检测技术［J］.无损检测，2010，32(8):612-615.

ZHANGJing，XIE She-juan，CHEN Zhen-mao.Direct current potential drop inspection technique for metallic foam［J］.Non-Destructive Testing，2010，32(8):612-615.

［5］ 万正军，廖俊必，王裕康，等.基于电位列阵的金属管道坑蚀监测研究［J］.仪器仪表学报，2011，32(1):19-25.

WAN Zheng-jun，LIAO Jun-bi，WANG Yu-kang，et al.Research on metal tubing Pit corrosion monitoring based on potential-array method［J］.Chinese Journal of Scientific Instrument，2011，32(1):19-25.

［6］ Wu Yinchuan，Guo Baolong，Zhang Jiatian.Study on defect detecting and locating method of tubular cylindrical conductor［J］.Telkomnika-Indonesian Journal of Electrical Engineering，2013，11(6):3251-3258.

［7］ WMingli，F Yu.Numerical calculations of internal impedance of solid and tubular cylindrical conductors under large parameters［J］.IEE Proc-Gener Transm Distrib，2004，151(1):67-72.

［8］ William H Hayt，John A Buck.Engineering Electromagnetics［M］.7th ed.Beijing:Tsinghua University Press，2009:320-325.