模拟地层条件的岩石抗钻特性

沈海超，刘 畅，王建宁，郑 力，田院生，万州亮

(中国石化集团国际石油勘探开发有限公司，北京100029)

地下岩石一般处于三向应力状态，其物性及力学特性与其所处应力及温度环境有关［1］。岩石抗破碎难易程度用抗钻特性参数描述，其中可钻性级值及单轴抗压强度应用广泛［2-7］，微钻头可钻性实验及单轴抗压实验分别是获取这2个参数最直接手段［8-10］;然而这2个实验均无法近似模拟地层环境，测量结果自然不能全面、客观评价地层条件下岩石抗钻特性。岩石三轴抗压强度表征了实际埋藏条件下岩石强度，辅以可钻性级值为参考，可较为客观地反映地层条件下岩石抗钻特性，目前这2个参数逐步受到业界重视，并开始应用于PDC钻头设计及优化、钻速分析［11-14］。三轴压缩实验是测量三轴抗压强度的直接方法，然而实验毕竟有限，难以全面反映三轴抗压强度沿井深的分层规律，制约着以三轴抗压强度为基础的钻头设计、优选及钻速预测，故基于实验建立可靠的三轴抗压强度连续剖面至关重要。

本文以模拟地层条件的岩石三轴抗压强度实验、波速实验以及可钻性实验为基础，通过实验数据多元回归分析分别建立可靠的三轴抗压强度及可钻性级值多因素模型，在此基础上，利用测井资料建立了岩石三轴抗压强度及可钻性级值连续剖面，揭示了抗压强度分层规律，为钻头设计、优选及钻速预测等提供技术支撑。

1 室内实验

1.1 三轴抗压强度实验

采用MTS伺服控制岩石力学三轴实验装置，该装置具有轴压、围岩、孔隙水压和温度独立闭环控制系统，可模拟地层条件进行岩石力学、超声波等参数测试。其主要技术指标:最高轴压2 000 kN、最高围压100 MPa、最高孔隙压力60 MPa、最高环境温度150℃。

实验岩心取自俄罗斯远东鄂霍次克海域V区块，根据岩心埋深，模拟地层温度、压力条件共进行了50组三轴抗压强度实验以及岩心波速测定。部分实验数据见表1所示，其中泥质体积分数为测井解释成果。

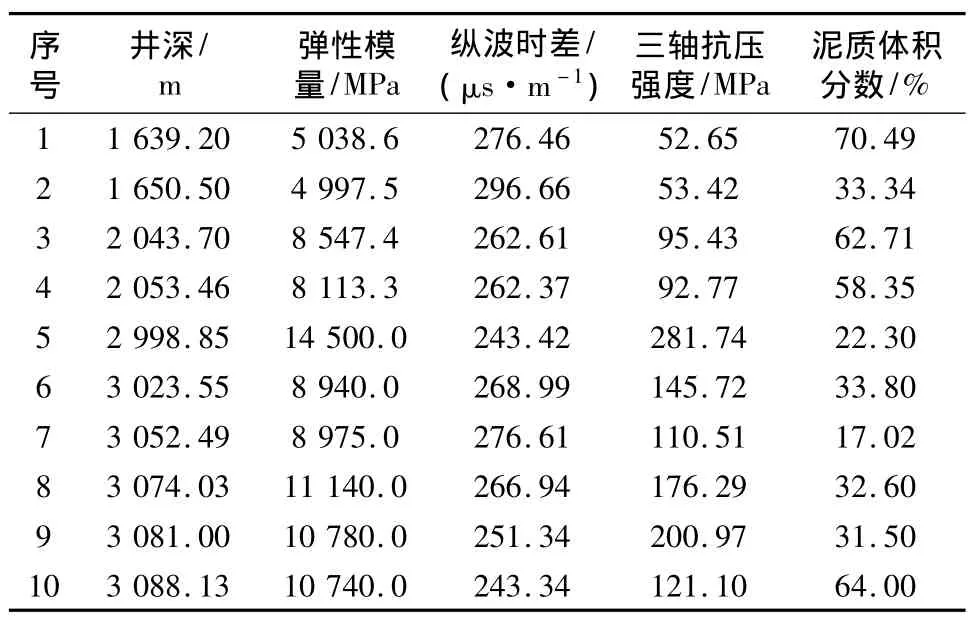
表1 三轴抗压强度及声波时差测量结果Tab.1 Testing results of triaxial compressive strength and acoustic travel time

1.2 微钻头可钻性实验

目前，岩石可钻性级值一般采用常温常压条件下的微钻头实验测定，实验采用特定规格微钻头，记录钻进一定深度(一般2.4 mm)所用的时间(钻时)，取2为底的对数，即为岩石的可钻性级值。划分标准:可钻性级值范围1～4为软地层、5～7为中等、8～10为硬地层。

考虑可钻性与岩石波速等物性参数相关性较强，通过模拟地层温度、压力条件进行岩石波速测量，回归得到可钻性级值与声波时差、密度等参数的相关模型，可相对客观地反映地层条件下岩石可钻性。

本研究进行了微钻头可钻性实验以及模拟地层温度、压力条件的岩心波速测量。其中波速测量结果与反映地层综合信息的声波测井结果吻合较好，说明本实验环境达到模拟地层条件的目的。部分实验数据见表2。

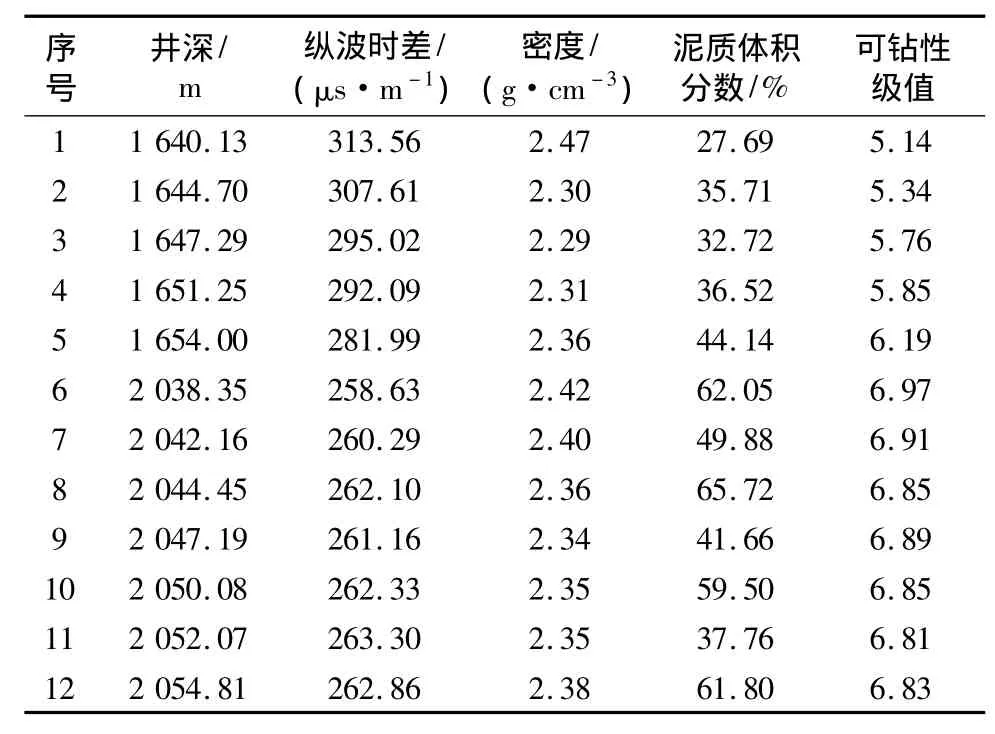
表2 V区块岩心声波时差与岩石可钻性级值Tab.2 Acoustic travel time and drillability grade value of cores in V block

2 抗钻特性参数相关模型的建立

2.1 可钻性级值多元回归模型

目前国内外有关岩石可钻性的关系模型很多，以与地层埋深、声波时差、密度及泥质体积分数等参数的单因素模型为主，其中可钻性与声波时差的关系最为普遍［15-18］，而岩石可钻性影响因素众多，单因素模型描述并不全面。

利用可钻性级值、波速等实验结果及泥质体积分数测井解释成果，采用多元回归分析方法，通过相关系数、标准差及F检验分析认为线性模型最佳，从而建立了可钻性级值与井深、纵波时差、密度及泥质体积分数的多因素线性模型

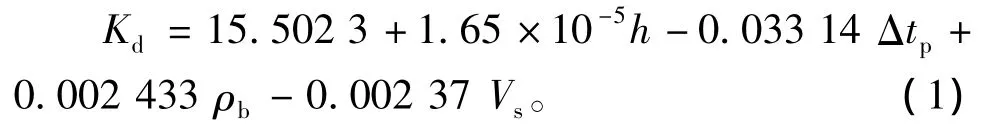
式中:Kd为岩石可钻性级值，无因次;h为埋深，m;Δtp为岩石纵波时差，μs/m;ρb为岩石密度，g/cm3;Vs为泥质体积分数，无因次。

该回归模型相关系数达89.3%，说明可钻性与井深、纵波时差、密度及泥质体积分数的相关程度较高;F显著性统计量为0.001 4，小于显著性水平0.05(置信度95%)，进一步说明回归效果显著，从而为建立可钻性连续剖面奠定了基础。

2.2 三轴抗压强度多元回归模型

目前国内外基于岩石单轴抗压强度优选钻头研究较多［7，11］，单轴抗压强度模型以其与弹性模量、泥质体积分数的关系模型为主，但均无法客观反映地层条件下岩石抗压强度特性。基于岩石三轴抗压强度实验及模拟地层条件的波速实验，采用多元回归分析方法，通过相关系数、标准差及F检验分析认为线性模型最佳，为此建立了岩石三轴抗压强度与弹性模量、纵波时差、泥质体积分数的多因素回归模型

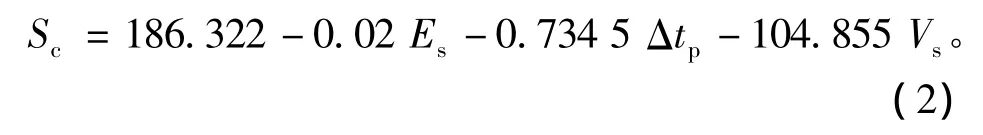
式中:Sc为岩石三轴抗压强度，MPa;Es为静态弹性模量，MPa。

该回归模型相关系数达84.63%，说明三轴抗压强度与弹性模量、纵波时差、泥质体积分数的相关程度较高;F显著性统计量为0.000 4，小于显著性水平0.05(置信度95%)，再次说明回归效果显著，从而为三轴抗压强度连续剖面的建立奠定了基础。

3 抗钻特性参数连续剖面的建立及应用

3.1 动静态弹性参数关系模型的建立

利用声波时差等测井资料，根据均匀介质声波速度与弹性参数的关系，可得到动态弹性模量及泊松比。但工程分析中需使用静态弹性参数，为此对实验得到的静态弹性参数以及测井资料计算得到的动态弹性参数进行回归分析，线性模型相关系数较高，从而建立了动静态弹性参数关系模型。

V区块动静态弹性模量回归相关系数为0.689 6，相关模型

式中:Ed为动态弹性模量，MPa;μs为静态泊松比，无因次;μd为动态泊松比，无因次。

3.2 抗钻特性参数连续剖面的建立

采用本研究提出的可钻性级值相关模型以及三轴抗压强度模型建立方法，利用测井声波时差等资料，结合泥质体积分数等测井解释成果，可建立可钻性级值及三轴抗压强度的连续剖面。V区块可钻性级值以及三轴抗压强度剖面分别如图1、图2所示。

根据地质分层，对地层抗钻特性参数分层描述，见表3。以三轴抗压强度为主，结合可钻性级值，较为全面、客观地反映地层条件下实际岩石抗钻特性，从而为钻头设计、优选及钻速预测提供更为可靠的依据。

3.3 指导意义及实例应用

3.3.1 指导PDC钻头设计及优化 目前PDC钻头应用广泛，然而其对地层强度等特性具有强敏感性，为提高钻头对地层适应性，必须根据地层特性进行PDC钻头设计与选型，而根据三轴抗压强度进行PDC钻头设计与选型已在国内外逐步兴起，并形成了一套指导PDC钻头切削结构参数设计方法［11-12］。基于本研究建立的三轴抗压强度连续剖面及发现的抗压强度分层规律等，参照当前国内外PDC钻头切削结构参数设计方法，分层设计理想PDC钻头参数，包括切削齿、刀翼、保径长度、冠部形状等，据此选择与之最为匹配的钻头，完成PDC钻头设计及选型。

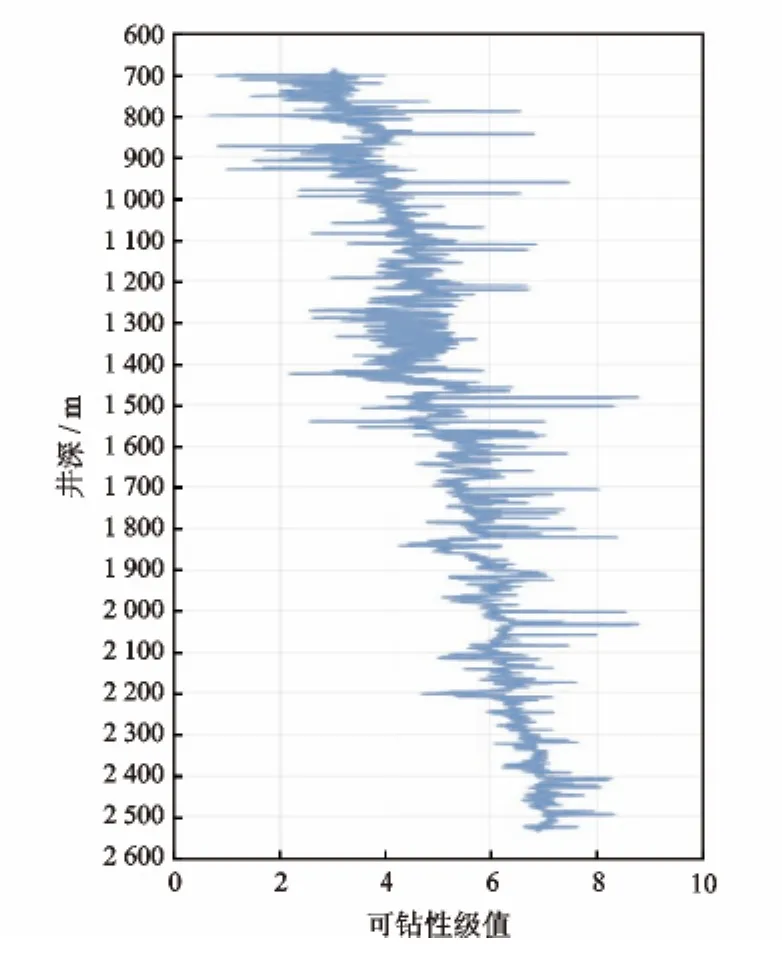
图1 V区块可钻性典型剖面Fig.1 Typical drillability profile in block V

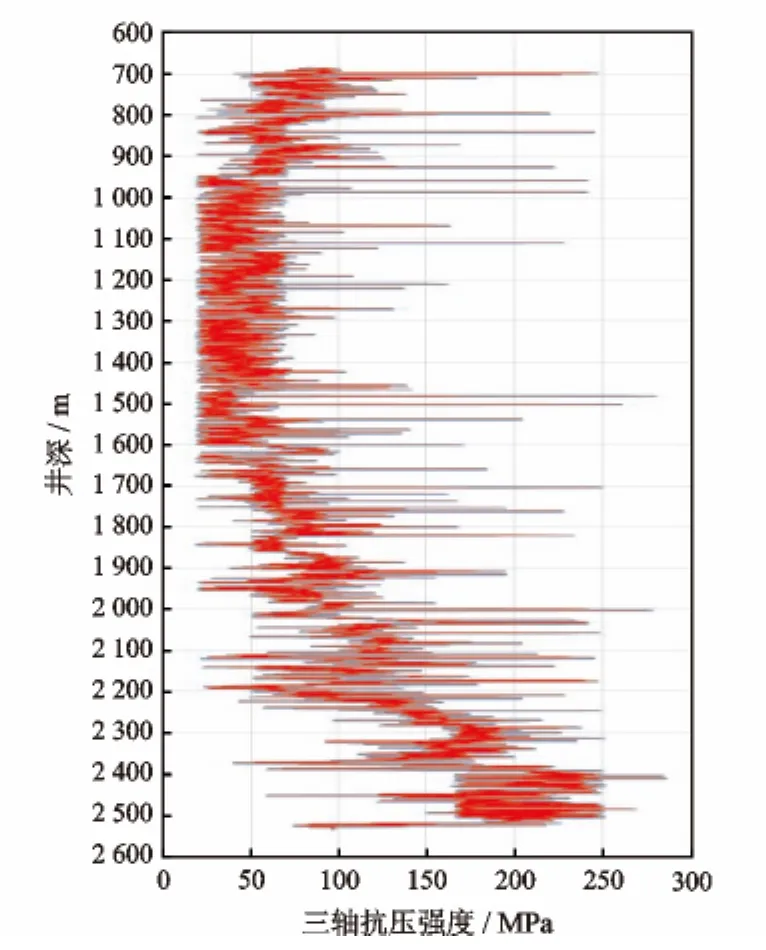
图2 V区块三轴抗压强度典型剖面Fig.2 Typical triaxial compressive strength profile in block V

表3 V区块地层抗钻特性参数分层描述Tab.3 Classification of formation anti-drilling performance of block V

以V区块可钻性较差、夹层多的四开Φ215.9 mm井段为例，对应井段约为1 800～2 530 m，根据强度特性分析该井段理想PDC切削结构参数为:切削齿数49、切削齿尺寸16 mm、刀翼数7、保径长度50.8 mm、冠部形状4型，最终优选出SMITH公司生产的型号为MI716的PDC钻头。现场应用表明，采用优化设计的PDC钻头，该井段平均钻速由原来的11.57 m/h提高到31.58 m/h，同时钻头寿命明显提高，首先实现了单只钻头打完四开进尺的目标。

3.3.2 指导钻速预测 以三轴抗压强度为基础的钻速预测新模型正逐步建立［13］，新模型较以往以单轴抗压强度为基础的模型客观全面、精度更高，然而，这些新模型推广应用受制于缺少可靠的三轴抗压强度剖面，本研究提出的基于实验建立三轴抗压强度关系模型及连续剖面的方法有效解决了这一瓶颈难题，为提高全井段钻速预测精度奠定了基础。

4 结论

(1)基于模拟地层条件的三轴抗压强度实验及波速实验，通过多元回归分析，分别建立了高可信度三轴抗压强度及可钻性级值相关模型。在此基础上，结合动静态弹性参数关系，利用测井资料建立了三轴抗压强度及可钻性级值连续剖面，提示了抗压强度分层规律，相对客观、全面地反映地层条件下岩石抗钻特性。

(2)提出一套基于实验建立高可信度三轴抗压强度连续剖面和寻找抗压强度分层规律的方法，为利用三轴抗压强度科学指导钻头设计与选型以提高全井段钻速预测精度提供了技术支撑。该方法在V区块应用成功，基于三轴抗压强度设计及优选的PDC钻头取得了显著的钻井提速及延长钻头寿命的综合效果。

［1］ 黄思静，单钰铭，刘维国，等.储层砂岩岩石力学性质与地层条件的关系研究［J］.岩石力学与工程学报，1999，18(4):454-459.

HUANG Si-jing，SHAN Yu-ming，LIU Wei-guo，et al.The relationship between mechanical parameters of rock and formation conditions of reservoir sandstone［J］.Chinese Journal of Rock Mechanics and Engineering，1999，18(4):454-459.

［2］ Uboldi V，Civolani L，Zausa F.Rock strength measurements on cuttings as input data for optimizing drill bit selection［C］.SPE 56441，1999.

［3］ 沙林秀，张奇志，贺昱曜.基于SDCQGA优化BP神经网络的岩石可钻性建模［J］.西安石油大学学报:自然科学版，2013，28(2):92-97.

SHA Lin-xiu，ZHANG Qi-zhi，HE Yu-yao.Modeling of rock drillability with BPneural network optimized by SDCQGA［J］.Journal of Xi＇an Shiyou University:Natural Science Edition，2013，28(2):92-97.

［4］ 刘向君，宴建军，罗平亚，等.利用测井资料评价岩石可钻性研究［J］.天然气工业，2005，25(7):69-71.

LIU Xiang-jun，YAN Jian-jun，LUO Ping-ya，et al.Evaluation on rock drillability by well logging data［J］.Natural Gas Industry，2005，25(7):69-71.

［5］ 邓理，李黔，高自力.岩石可钻性评价方法研究新进展［J］.钻采工艺，2007，30(6):27-29.

DENG Li，LI Qian，GAO Zi-li.New evaluation method of rock drillability［J］.Drilling ＆ Production Technology，2007，30(6):27-29.

［6］ Robin Joseph Andrews，Geir Hareland，Thomas WEngler，et al.Methods of using logs to quantify drillability［C］.SPE 106571，2007.

［7］ 卫增杰.基于声波测井资料的川西地区深层岩石单轴抗压强度预测［J］.石油天然气学报，2011，33(1):111-114.

WEI Zeng-jie.Prediction of uniaxial compressive strength of deep rock in western Sichuan based on acoustic logging data［J］.Journal of Oil and Gas Technology，2011，33(1):111-114.

［8］ 朱澄清，杨迎新，廖忠会.川西须家河深层岩石力学性质及可钻性研究［J］.钻采工艺，2010，33(5):29-31.

ZHU Cheng-qing，YANG Ying-xin，LIAO Zhong-hui.Study on mechanical property and drillability of rock in Sichuan Xujianhe deep reservoir［J］.Drilling ＆ Production Technology，2010，33(5):29-31.

［9］ 李士斌，阎铁，韩辉.模拟井底应力条件下的岩石可钻性实验研究［J］.天然气工业，2003，23(2):64-66.

LI Shi-bin，YANTie，HANHui.Drilliability test study under modeling conditions of bottom hole stress［J］.Natural Gas Industry，2003，23(2):64-66.

［10］郑德帅，高德利，冯江鹏.实钻条件下井底岩石可钻性预测模型研究［J］.岩土力学，2012，33(3):859-863.

ZHENG De-shuai，GAO De-li，FENG Jiang-peng.A model for downhole rock drillability prediction under real drilling condition［J］.Rock and Soil Mechanics，2012，33(3):859-863.

［11］张召平，苏新亮，葛洪魁.利用岩石三轴抗压强度优选PDC钻头［J］.石油大学学报:自然科学版，2005，29(6):38-40.

ZHANG Zhao-ping，SU Xin-liang，GE Hong-kui.Selection of polycrystalline diamond compact bits based on triaxial compressive strength of rock［J］.Journal of the University of Petroleum，China:Edition of Natural Science，2005，29(6):38-40.

［12］吴应凯，王国华，蒋建伟.莫深1井PDC钻头优化设计及应用［J］.新疆石油天然气，2008，4(9):17-21.

WU Ying-kai，WANG Guo-hua，JIANG Jian-wei.The optimum design of PDC bit in MS-1 well and its application［J］.Xinjiang Oil＆ Gas，2008，4(9):17-21.

［13］Hector U Caicedo，William M Calhoun，Russ T Ewy.U-nique ROP predictor using bit-specific coefficient of sliding friction and mechanical efficiency as a function of confined compressive strength impacts drilling performance［C］.SPE-92576-MS，2005.

［14］Prasad B Kerkar，Geir Hareland，Ernesto R Fonseca，et al.Estimation of rock compressive strength using downhole weight-on-bit and drilling models［C］.IPTC-17447，2014.

［15］张召平，翁行芳.中原油田岩石可钻性与声波时差关系研究［J］.石油钻探技术，2006，34(6):11-13.

ZHANG Zhao-ping，WENG Xing-fang.A study on the relationship between rock drillability and acoustic travel time［J］.Petroleum Drilling Techonology，2006，34(6):11-13.

［16］梁启明，邹德永，张华卫，等.利用测井资料综合预测岩石可钻性的实验研究［J］.石油钻探技术，2006，34(1):17-19.

LIANG Qi-ming，ZOU De-yong，ZHANG Hua-wei，et al.Prediction rock drillability by well logging:An experimental research［J］.Petroleum Drilling Techonology，2006，34(1):17-19.

［17］王忠福，孟金城，张志邦.声波时差测井在岩石可钻性预测中的应用［J］.大庆石油地质与开发，2006，25(3):94-96.

WANG Zhong-fu，MENG Jin-cheng，ZHANG Zhi-bang.Application of acoustic travel time logging in rock drillability prediction［J］.Petroleum Geology ＆ Oilfield Development in Daqing，2006，25(3):94-96.

［18］张厚美，陈恩强，楼一珊.声波时差用于钻头选型的研究［J］.中国海上油气:工程，1997，9(1):34-38.

ZHANG Hou-mei，CHEN En-qiang，LOU Yi-shan.A study on the bit selection applying interval transit time［J］.China Offshore Oil and Gas:Engineering，1997，9(1):34-38.