同轴超短焦距折反式投影系统设计

杨建明1,2∗,刘伟奇1,孟祥翔1,2,冯 睿1,孟 中1,张大亮1

(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033; 2.中国科学院大学,北京100049)

同轴超短焦距折反式投影系统设计

杨建明1,2∗,刘伟奇1,孟祥翔1,2,冯 睿1,孟 中1,张大亮1

(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033; 2.中国科学院大学,北京100049)

为了缩短超短焦距投影仪的机械总长,克服传统离轴超短焦距投影系统的装调困难,降低系统的设计难度,设计了一种同轴的超短焦距投影系统。首先,通过分析像差与系统总长的关系,证明了需要保证系统总长的必要性。然后,通过镂空非球面反射镜中心部分,利用平面或球面反射镜折转光路,提出了一种新的设计超短焦距投影仪的方法。在保证光学总长的同时缩短了机械总长,提高了空间利用率,解决了同轴折反系统中存在挡光的问题。最后设计的系统总长为215 mm,投射尺寸为100 in。系统的投射比为0.17,物方NA为0.2,焦距为1.66 mm。各个视场传递函数在内奎斯特频率处达到0.5以上,各指标都满足了投影系统的要求。同时,在透镜个数相同的情况下,系统的性能都优于传统的投影仪。

光学设计;投影系统;折反射系统;超短焦距

1 引 言

目前投影机向微型化、立体化和超短焦距发展,微型投影机又称口袋式投影,主要特点是把传统庞大的投影机精巧化、便携化[1],使投影技术更加贴近生活和娱乐;立体投影技术主要研究如何显示出三维的立体图像,增强体验感[2-3];而超短焦距投影仪的突出优点是即使在狭窄的空间也能实现大屏幕高质量的图像显示。虽然传统投影机可以投射出超大的显示画面,但投射距离很大。投影机的投射比越小,说明相同投影距离,投射画面的宽度越大。普通投影机的投射比通常在1.5～1.9之间;当投射比小于1时,即为短焦镜头;而当投射比在0.6以下,则是超短焦镜头。超短焦镜头由于制作工艺复杂,因此一直很昂贵,但是,由于超短焦投影机在教育行业等特殊应用上的先天优势,一直也受到用户的青睐,尤其在欧美地区,超短焦投影机在逐渐普及。

为了实现超薄化,必须增大投影镜头的视场角,起初的大视场投影仪都采用透射式设计,但是随着视场角的增大,各种轴外像差、色差等也急剧变化,并且很难同时得以校正,表现为非中心视场区域的各色图像是错位的,这样降低了图像的对比度,图像达不到满意的效果,同时大视场系统畸变也很难矫正,给光学设计带来很大的困难[4-5]。因此大视场透射式投影系统镜片数目大多结构复杂[6-7],另外,透射式投影系统不能距离屏幕太近,因为投影仪本身会遮挡投影图像。

Jun Ogawa等使用4片反射镜设计了短焦距投影系统[8],由于全反射系统没有色差,所成图像具有很好的清晰度和很高的对比度。可以在65 cm的投影距离下产生100 in(1 in＝2.54 cm)的画面。孙旭涛等[9]用Zernike自由曲面设计反射式投影系统可以使系统更薄。由于全反射系统需要完全采用离轴式设计,机械结构比较庞大,这必然加重了加工和装调的精度要求,实现产业化、批量化也存在一定的困难。

本文对非球面反射镜产生的像差进行了计算,分析了系统总长与像差矫正难度的关系。提出了一种同轴的超短焦投影结构,利用镂空中心的非球面反射镜和一个折转镜,提高了系统的空间使用率,降低了传统离轴结构的装调困难。

2 超短焦投影系统的像差分析

将折射式镜头和反射式镜头相结合进行设计是实现超薄投影的最有效方法[9-11],由于这种折反射镜头属于大视场,小出瞳直径的系统,因此主要考虑的像差有场曲、像散、色差和畸变。与折射式系统不同,在折反射系统中,折射透镜不需要矫正像散和场曲,反而要产生足够的像散和场曲,来抵消反射镜的影响。其基本成像原理是通过折射镜头产生正的匹兹凡场曲和,同时产生负的像散,并校正色差、慧差和球差,然后采用反射镜校正畸变,抵消折射透镜组的正场曲和负像散。从而实现整个背投机身的超薄结构。系统结构如图1所示。

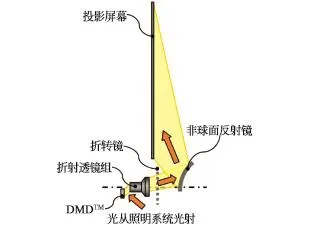
图1 典型的折射反射结合投影系统Fig.1 Representative refractive-reflective projection system

这种折反式的主要缺点是图像源到非球面反射镜之间的距离很长,达到400 mm以上。为了减小系统总长,最常用的方法是用平面反射镜(折转镜)折转光路,但是加入平面反射镜后,非球面反射镜与透镜组就处于非同轴状态,对装调带来了很多不便,增加了成本并降低了系统的稳定性,阻碍了超薄投影的进一步普及。

在折反射结合的投影系统中,非球面反射镜的存在使得这种结构完全不同于传统折射式投影系统,因此对非球面反射镜的像差贡献分析显得尤为重要。同时,由于反射面为非球面且系统为非近轴光学系统,不能简单地使用初级像差理论进行分析。因此,本文通过计算非球面反射镜的曲率变化,来分析像差的规律。

系统所采用的为偶次非球面,其曲线方程为:

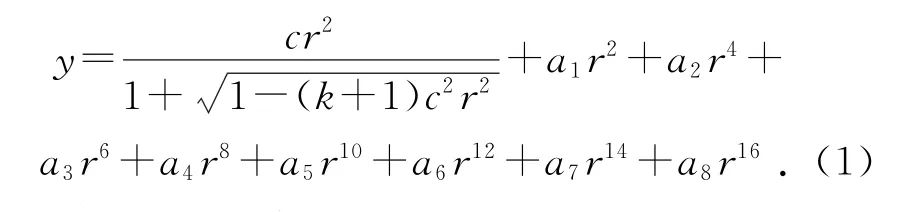
图2为非球面反射镜的三维图,可以认为非球面是曲线(1)通过绕y轴旋转生成的,因此其曲面方程可以通过

代换得到。其中x、z为垂直旋转轴y的坐标轴。曲线的曲率方程为:

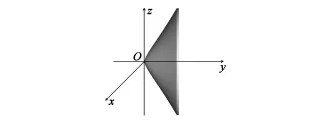
图2 非球面反射镜Fig.2 Aspheric mirror

将式(2)代入式(1),并令x＝0,得到子午面内方程,通过求导变换,代入式(3),即可求出非球面子午方向的曲率。将式(2)代入式(1),计算x＝0处的一阶导数和二阶导数:

将式(4)和式(5)代入式(3),即可求出x＝0的平面内,非球面各个z坐标处弧矢方向的曲率。由于非球面方程比较复杂,本文通过Matlab符号运算计算出了结果。

折返式超薄投影系统可以分为3个部分:折射透镜组,非球面反射镜以及投影屏幕。折射透镜组的光学总长很短,对投影仪的机身尺寸基本没有影响;非球面反射镜与投影屏幕之间的距离属于机身外部距离。与投影仪的机身尺寸无关。决定投影仪机身尺寸的主要因素为透镜组到非球面反射镜之间的距离D,因此,在其他条件不变的情况下,本文分析了D与非球面面型的关系,从而间接分析了系统总长与像差的制约关系。表1列出了使用传统超薄投影结构,保持投影屏幕尺寸不变,并且畸变矫正到1%以内的情况下,D分别为280 mm 和200 mm时所对应的非球面参数。

表1 不同距离下非球面反射镜参数Tab.1 Parameters of aspheric mirrors in different distance

图3为非球面反射镜的曲线图,横坐标为口径值,纵坐标为矢高值,其中实线为长距离时对应的非球面曲线,虚线为短距离时所对应的非球面曲线,可以看出随着D变小,非球面变的更凸。

图3 不同距离对应的非球面曲线Fig.3 Curves of aspheric in different distance

图4为不同距离下非球面子午和弧矢方向的曲率随口径坐标的变化关系,横坐标为口径值,纵坐标为曲率值,其中大值所对应的是弧矢面内的曲率,小值所对应的为子午面内的曲率。首先,随着口径逐渐增大,子午和弧矢面内曲率值逐渐减小。因此非球面反射镜的焦距随着口径的增大而增大,根据反射面焦距公式,子午面内口径大于45 mm后,曲率趋于零,焦距接近无穷大,近似为无焦平面。不同口径处焦距的剧烈变化,导致非球面反射镜产生了很大的场曲。子午面内的曲率小于弧矢面内的曲率,说明在同一点处,非球面的子午方向和弧矢方向具有不同的焦距,导致非球面产生了像散;其次,子午方向,在相同口径处,短距离时所对应的曲率值大于长距离所对应的曲率,说明D越短,非球面产生的场曲越大。图5为不同距离下子午曲率与弧矢曲率差值的变化规律。纵坐标对应了同口径处子午曲率和弧矢曲率的差值,短距离所对应的差值大,说明D越短,像散越严重。

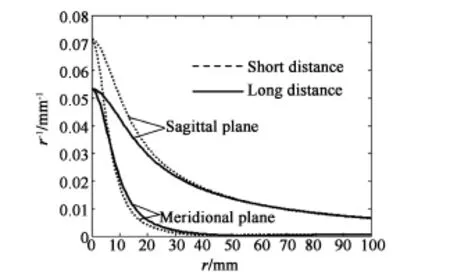
图4 不同距离对应非球面的弧矢和子午曲率Fig.4 Sagittal and meridional curvature of asphere in different distance

图5 非球面同一点弧矢和子午曲率差值Fig.5 Difference of aspheric sagittal and meridional curvature in the same point

3 设计原理

由以上分析得出,非球面反射镜不可避免地产生了比较大的场曲和像散,而且像散和场曲随着D变小而增大。这是要保证长距离的主要原因。同时,D变小使得折射透镜组的光焦度变大,随之而来的像差也会增大。

为了缩短系统机械总长,保持长的光学总长,同时使系统处于同轴状态,本文提出的解决方案如图6所示。考虑到在折反投影系统中,所使用的光线为轴外光线,不是轴上光线和近轴光线,这为设计同轴系统提供了可能性。系统中各个元素同轴摆放,将投射镜M1中心部分AB镂空,使得折射透镜组发出的光可以透过M1中心而不被遮挡,并投射到一个小尺寸的球面或者平面折转镜M2上,然后M2将光反射到投射镜M1上,最后到达投影屏幕。光线经过M2反射到M1镜时,必须保证最小视场角光线在B点的投射高度大于最大视场角光线从折射透镜组发出经过M1时的高度,以保证最小视场光线可以正常地被M1反射,并且最大视场光线不被M1遮挡,这样可以实现了超薄投影的同轴化。

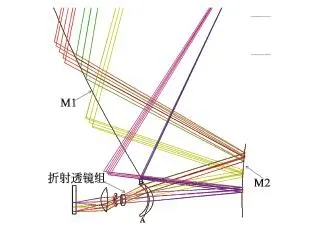
图6 同轴折射反射结合投影系统原理图Fig.6 Principle of coaxial refractive-reflective projection system

4 设计结果

通过所述方法,本文设计投射尺寸为100 in的系统。采用TI公司的0.65 in数字微反射镜片(DMD)作为光学引擎进行数字光学调制,其解析度为1 920×1 080(16∶9),像元大小为7.5 μm。微反射镜片依靠反射光线进行工作,光能利用率高,能够实现色彩逼真还原和高清晰度要求。设计时物面为DMD,像面为投影屏幕,为了保证足够的像面照度,系统设定DMD的NA为0.2。为进一步简化系统,反射镜M2设定为平面镜。系统中使用了2个非球面透镜,为便于加工,非球面材料为光学塑料PMMA。图7(a)为系统折射部分精细结构,图3(b)为整体效果图。

图7 (a)折射透镜结构,(b)系统整体光路图Fig.7 (a)Structure of refractive lens;(b)Layout of the system

系统光学指标如表2。其中主光线角度(Chief Ray Angle)表示DMD每个像元的主光线与DMD法线的夹角,CRA影响光能利用率及系统的照度均匀程度,为达到良好的均匀性及光能利用率,CRA需要控制在2°以内。

传统折射式投影系统的投射比E的计算表达式为:其中W为投影屏幕宽度,L为投影屏幕距离投影仪最近一面的距离。在超薄系统中,L很小,且与投影仪尺寸相当,为更好地说明超薄的性能,L定义为投影系统距离屏幕最远的距离。

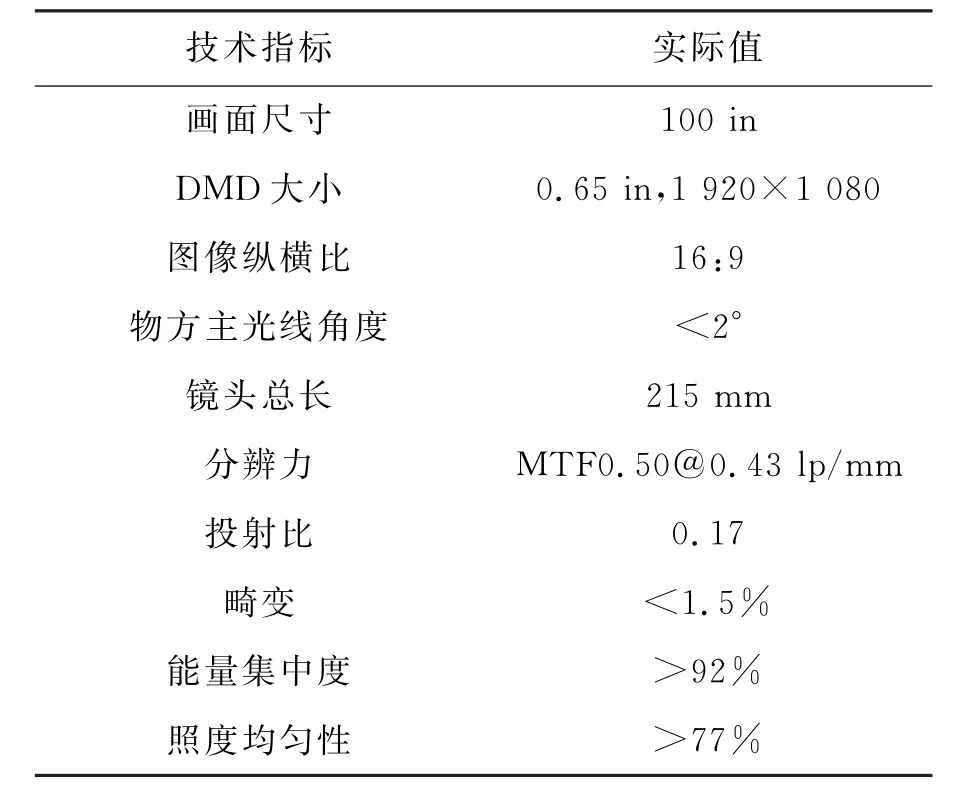
表2 成像物镜的各项技术指标Tab.2 Various specifications of the projection lenses

表3列出从第一个透镜开始,系统各个面曲率半径、厚度、材料和非球面的圆锥系数。其中最高折射率的玻璃为ZF50,其折射率为1.74。表4为非球面系数,每个面的代号与表3一致。

表3 系统中的常规参数Tab.3 Conventional parameters of the system

表4 系统中非球面参数Tab.4 Aspheric parameters of the system

4.1 性能评价

根据光学技术指标要求,通过ZEMAX®软件进行了成像质量分析。由于DMD像元大小为7.5 μm,放大155倍后对应于画面像元大小为1 162 μm,其奈奎斯特频率为0.43 lp/mm,图8表示不同视场下镜头的MTF曲线,所有视场在此频率下都大于0.5,从MTF曲线可以看出,子午和弧矢之间差值比较大,说明系统中存在比较明显的像散。图9为系统的网格畸变,系统的最大畸变小于1.5%。

图8 调制传递函数曲线Fig.8 Curves of modulation transfer Function

图9 网格畸变图Fig.9 Grid distortion

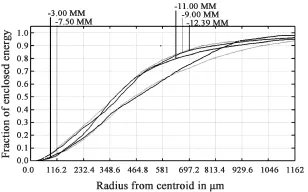
图10 能量集中度曲线Fig.10 Curves of geometrical encircled energy

图10为系统的几何能量集中度曲线,横坐标表示从边缘到质心的弥散圆半径大小,纵坐标表示此半径内所占的能量比例,最大坐标值即为投影系统对应的像元尺寸。所有视场在一个像元尺寸内的能量集中度均大于92%。图11为系统的相对照度曲线,相对照度最小值为77%。通过照明系统微透镜阵列的调节[12]以及对源图像的调整,可以使最后显示的图像照度均匀。

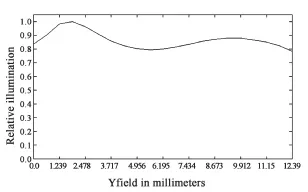
图11 相对照度曲线Fig.11 Curves of relative illumination

用ZEMAX®图像模拟功能对长宽比为16∶9的图片进行了模拟,此功能可以给出系统直观综合的成像效果。图12为原图片,图13为仿真结果。分析结果表明,系统的成像质量良好,满足投影系统的要求。

图12 原图片Fig.12 Original image

图13 图像仿真结果Fig.13 Image simulation result

5 结 论

为了降低超薄投影的成本和装调难度,使超薄投影仪更具市场价值,本文提出了一种系统总长小且同轴的投影机光学系统,解决了目前超薄投影系统中为了压缩总长而使系统处于离轴的问题。投射尺寸为100 in时,系统总长为215 mm,投射比为0.17。通过镂空非球面反射镜中心,同时使用平面或者球面反射镜折转光路,解决同轴光束遮挡的问题。在空间上虽然压缩了总长,但是光程总长并没有缩短,这样没有增大设计难度,并且提高了空间利用率。文章首先介绍了超薄投影系统的原理以及主要的像差贡献,其次对同轴投影系统的设计原理进行了说明,最后对设计结果进行分析。从MTF曲线上反映出系统存在明显的像散,这与前面的理论分析基本一致。

[1] 赵星,吴宏超,宋丽培,等.微型投影机自由曲面LED聚光器的设计[J].光学精密工程,2010,18(10):2124-2128.Zhao X,Wu H C,Song L P,et al.Design of freeform LED concentrator for micro-projector[J].Optics and Precision Engineering,2010,18(10):2124-2128.(in Chinese)

[2] 马建设,张波常,苏萍,等.应用微柱透镜的自由立体前投影屏幕设计[J].液晶与显示,2013,27(6):760-763.Ma J S,Zhang B C,Su P,et al.Autostereoscopic front projection system based on micro-lenticular lens array[J].Chinese Journal of Liquid Crystals and Displays,2013,27(6):760-763.(in Chinese)

[3] 康玉思,田志辉,刘伟奇,等.激光显示广角球幕投影镜头设计[J].液晶与显示,2013,28(3):330-337.Kang Y S,Tian Z H,Liu W Q,et al.Wide-angle dome-screen projection lens design of laser display[J].Chinese Journal of Liquid Crystals and Displays,2014,29(3):333-336.(in Chinese)

[4] Yang J M,Liu W Q,Lv W＠Z,et al.Method of achieving a wide field-of-view head-mounted display with small distortion[J].Opt.Lett.2013,38(12):2035-2037

[5] 卢海平,刘伟奇,康玉思,等.超大视场头盔显示光学系统设计[J].光学精密工程,2012,20(5):979-987.Lu H P,Liu W Q,Kang Y S,et al.Design of compact optical system in wide-angle head mounted display[J].Optics and Precision Engineering,2012,20(5):979-987.(in Chinese)

[6] Kuwata M,Sasagawa T,Kojima K,et al.Wide angle projection optics for compact rear projector[J].SID’05 Digest,70(3):1918-1921.

[7] Gohman J A.Wide-angle projection lens[P].U.S.Patent 7175287_2007.

[8] Ogawa J,Agata K,Sakamoto M,et al.Super-short foeus front projectior with aspheric mirror projection optical system[J].SID’05 Digest,13(2):111-116.

[9] 孙旭涛.应用自由曲面的超薄投影显示系统理论和实验研究[D].杭州:浙江大学,2008.Sun X T.Application of free-form surface of ultra-thin projection display systems theory and experimental research [D].Zhejiang:Zhejiang University,2008(in Chinese)

[10] Shikama S,Suzuki H.Optical system of ultra-thin rear projector equipped with refractive-reflective projection optics[J].SID 02 Digest 46.(2)1250-1253.

[11] 康玉思,田志辉,刘伟奇,等.超薄前投激光显示系统研制[J].应用光学,2012,33(5):832-836.Kang Y S,Tian Z H,Liu W Q,et al.Ultra-thin front projector for laser display system.[J].Journal of Applied Optics,2012,33(5):832-836.(in Chinese)

[12] 李丹,薛芸芸,曹雯,等.基于微透镜阵列的DMD芯片投影系统照明优化[J].光学学报,2013,33(1):0122002-1-0122002-4.

Li D,Xue Y Y,Cao W,et al.Optimization of DMD illumination system with microlens array[J].Acta Optica Sinica,2013,33(1):0122002-1-0122002-4.(in Chinese)

Design of coaxial short focal length catadioptric projection system

YANG Jian-ming1,2∗,LIU Wei-qi1,MENG Xiang-xiang1,2, FENG Rui1,MENG Zhong1,ZHANG Da-liang1

(1.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences, Changchun 130033,China; 2.University of Chinese Academy of Sciences,Beijing 100049,China)

A new type of coaxial ultra short focal projector was designed in order to reduce the alignment difficulty,reduce the difficulty of system design and shorten the total length.Firstly,by analyzing the relationship between the system’s total length and the aberration,the necessity of ensuring a long system’s total length is proved.Then,through hollowing the central portion of an aspherical mirror and using a plane or spherical mirror to deflecting the optical path,a new design method for ultra short focal length projector is presented.It solves the blocking problem existing in the coaxial catadioptric optical system and improves the space utilization rate by ensuring a long total optical length and shortening the overall machinery length.Finally,the system’s screen size is 100 in and the total length of 215 mm.The focal length is 1.66 mm and the object NA is 0.2 with 0.17 throw ratio.The MTFs of every field are over 0.5 at the Nyquist Frequency.All of the indexes meet the demand of theprojective system.Meanwhile,in the case of the same number of lenses,the system’s performance is better than the conventional projector.

optical design;projection system;catadioptric system;ultra short focal

TN141

:A

10.3788/YJYXS20153005.0864

1007-2780(2015)05-0864-08

杨建明(1989－),男,甘肃定西人,博士研究生,主要从事投影仪及头盔显示系统的研究。E-mail: yangjm2007＠lzu.cn.

刘伟奇(1958－),男,吉林长春人,博士生导师,研究员,主要从事激光显示技术、空间目标成像与瞄准技术等方面的研究。E-mail:liuwq＠ciomp.ac.cn

2014-09-26;

:2014-10-29.

国防基础科研计划(No.B1720132001)

∗通信联系人,E-mail:yangjm2007＠lzu.cn