卫星姿控系统的滑模容错控制及主动振动抑制

杨婧，史小平

（哈尔滨工业大学控制与仿真中心，黑龙江哈尔滨150080）

卫星姿控系统的滑模容错控制及主动振动抑制

杨婧，史小平

（哈尔滨工业大学控制与仿真中心，黑龙江哈尔滨150080）

针对执行机构故障情况下挠性卫星姿态控制系统的容错控制及主动振动抑制问题，建立轨控推力扰动条件下含执行器故障的挠性卫星姿态控制系统模型，采用自适应控制方法设计该姿控系统的高阶滑模容错控制器，并在姿态稳定的基础上设计基于高阶滑模的补偿项以降低挠性振动对姿态精确度的影响。对轨控期间飞轮正常情形及故障情形下的挠性卫星姿态仿真结果表明，在卫星姿态控制系统存在干扰的条件下，该方法能实现对执行器故障的容错能力并能提高姿态控制精确度。

高阶滑模控制；主动振动抑制；挠性卫星；容错控制

0 引 言

安全性和可靠性一直是卫星控制系统设计时亟需考虑的问题［1］。现代大型应用卫星主要由中心刚体和挠性结构组成，由于这两者存在着强耦合，挠性结构的弹性振动将导致卫星主体的姿态振荡。另外，由于在轨卫星长期工作在温差大、失重及辐射强的恶劣环境中［2-4］，不可避免受到来自环境的各种干扰，为了保证其顺利完成指定任务，有必要建立相应的容错机制来提高系统的安全性及可靠性。近些年来，人们对挠性卫星姿态控制系统容错控制［5-6］及主动振动抑制［7-8］方面展开了大量研究，该类研究成果已相当丰富。然而在这些已有的挠性卫星研究成果中，对于轨道推力控制期间的姿态系统容错控制及主动振动控制算法研究则比较少。

对于进行轨道调控期间的挠性卫星，由于轨道控制推力会激起星体上挠性附件的振动，进而对卫星的质心运动与姿态运动产生影响，并引起卫星轨道质心平动运动与姿态转动运动的耦合。由于轨道推力控制期间挠性卫星所受到的扰动力矩已远大于其他运行阶段的扰动力矩［9-10］，因此，为了保证轨控期间挠性卫星姿态控制系统的稳定，采取适当的容错控制及主动振动抑制措施很有必要。

由于滑模控制算法简单、且对系统参数变化及干扰影响具有良好的鲁棒性［11］，因此在航天器容错控制领域得到广泛应用。与普通滑模容错控制相比，高阶滑模控制算法不仅具备普通滑模的优点，而且能有效地抑制抖振现象，提高控制精确度，并消除了相对阶的限制［12］。目前，在航天器姿态控制领域，主要研究成果以普通滑模控制居多，高阶滑模控制已有部分研究成果：文献［13-14］将高阶滑模姿态跟踪控制方法运用于空间飞行器，并在改善系统鲁棒性，及振颤抑制上取得了良好的控制效果。文献［15］针对航天器角速度镇定问题设计了高阶滑模控制器。

本文针对执行机构故障条件下的卫星姿态控制系统，结合自适应控制方法采用高阶滑模控制方法中的超扭曲算法设计了容错控制器。同时，针对轨控期间推力引起的挠性附件振动，设计了高阶滑模主动振动抑制补偿器来实现振动模态快速衰减。最后，基于此方法对几种不同情形下的轨控期间挠性卫星姿态控制系统进行仿真实验，并给出了仿真结及相应结论。

1 系统建模

1.1 轨控期间挠性卫星动力学及运动学模型

卫星轨道控制期间，在考虑轨控推力影响的条件下，伪坐标lagrange方法建立的系统动力学模型可表示为［9］

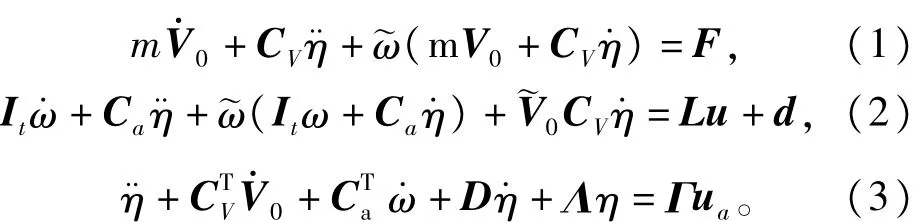
其中m∈R表示挠性卫星的总质量；V0= ［V0xV0yV0z］T∈R3表示卫星的平动速度；ω=［ωxωyωz］T∈R3表示卫星本体坐标系相对于惯性坐标的姿态角速度矢量在本体系上的投影；η= ［ηxηyηz］T∈R3表示卫星挠性附件的振动模态；F∈R3表示轨道控制期间的推力矢量；It∈R3×3表示卫星的正定对称转动惯量矩阵；L∈R3×3表示卫星反作用飞轮的安装矩阵；u∈R4表示反作用飞轮提供的控制力矩矢量；d=［dxdydz］T∈R3表示卫星运行期间受到的扰动力矩；CV、Ca∈R3×3分别表示挠性附件的挠性振动运动与星体平动运动、星体转动运动的耦合系数矩阵；Λ=diag（）表示挠性模态的刚体矩阵；D=diag（2εω，1n12ε1ωn2，2ε1ωn3）表示挠性模态的阻尼矩阵；Γ表示主动振动控制元件与挠性附件间的耦合系数矩阵，ua表示主动振动控制输入矢量；并且定义

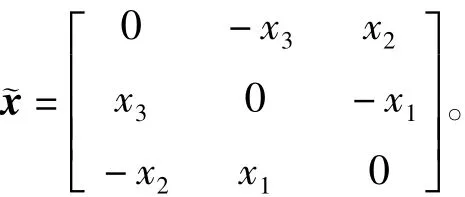
其中x=［x1x2x3］T∈R3。

利用四元数描述的卫星姿态运动学方程可表示为

1.2 执行器故障模型

考虑执行机构乘性故障及加性故障这两种故障类型，当执行机构发生这两种故障时可表示为

其中：uf表示故障情况下的执行器控制矢量；Δ= diag（Δ1，Δ2，Δ3，Δ4）表示恒值偏差故障；E= diag（e1，e2，e3，e4）表示执行器的故障矩阵；ej表示失效因子且满足

1.3 故障条件下的姿态系统模型

0（3）可知

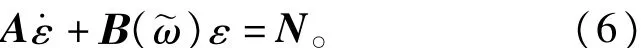
其中

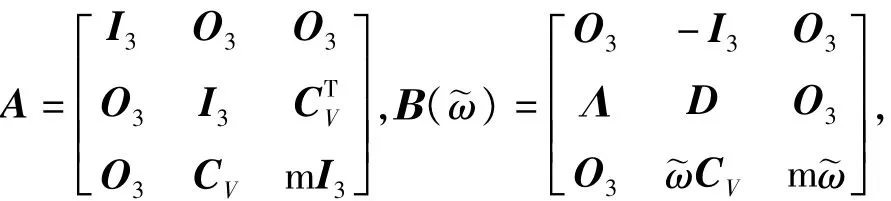
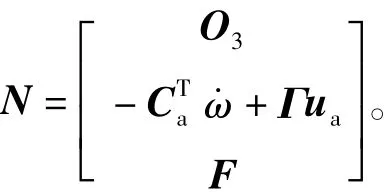
考虑执行器故障（5），则式（2）可表示成

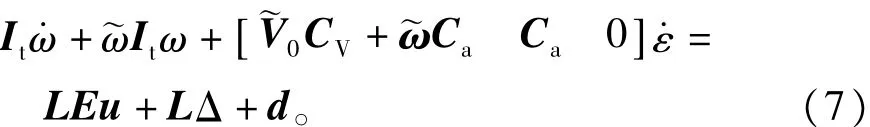
由式（6）可知

将式（8）代入式（7）整理得

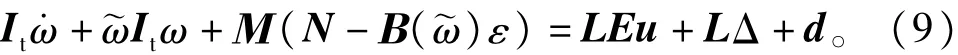
其中

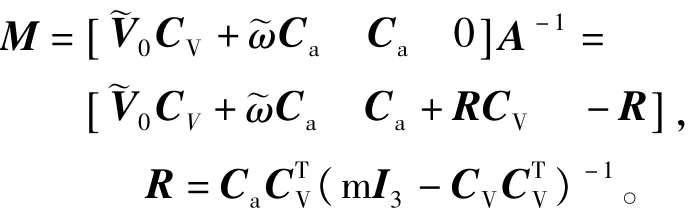
由于

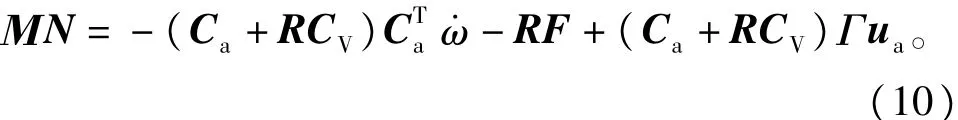
将式（10）带入式（9）可知，式（9）进一步可整理为

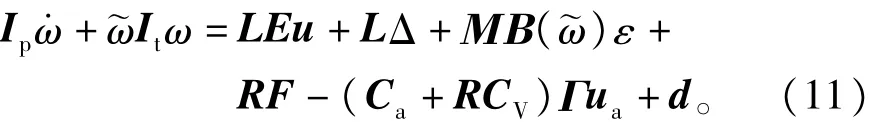
其中Ip=It-（Ca+RCV）

结合卫星姿态运动学方程可知：故障条件下轨控期间挠性卫星姿态控制系统可表示为

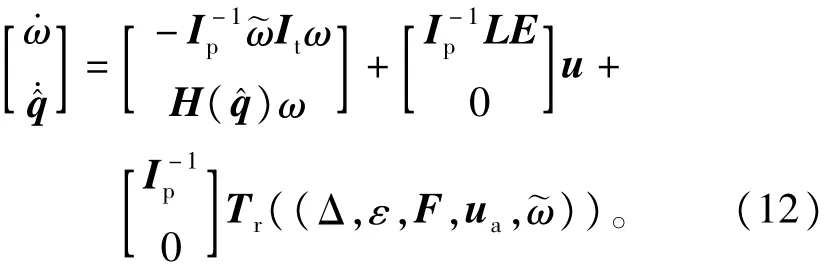
其中：

问题描述如下：

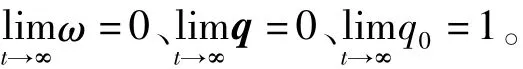
进一步，为提高姿态控制精度，并解决挠性结构弹性振动引起的卫星主体的姿态振荡问题，研究挠性附件主动振动问题，该问题描述如下：

2 容错控制器设计

超扭曲算法作为高阶滑模控制算法的一种，可以在有效时间内将滑模变量及其一阶导数收敛到零，并对抖振现象有良好的抑制效果［13-14］，该算法的收敛性见如下引理。

引理［11］考虑由式（13）描述的扰动条件下的非线性方程

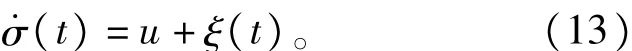
其中：u=-ρ｜σ（t）｜1/2sgnσ（t）-τ∫sgnσ（t）d t为超扭曲算法；ξ（t）表示有界的未知干扰，并且满足t）｜≤C，C表示干扰的导数的上界；σ（t）表示状态量；ρ和τ均为常系数。

为了实现姿态的快速稳定及对普通滑模算法中‘抖振’现象的抑制，采用超扭曲算法来实现对系统执行机构故障的容错构能力，并结合自适应控制算法来实现对干扰的抑制。

构造滑模变量如下

其中β＞0为一正实数。

由式（14）可知

假设1总扰动量Tr有界，即满足‖Tr‖≤k1，其中k1＞0为未知正实数。

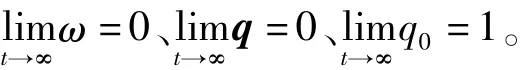
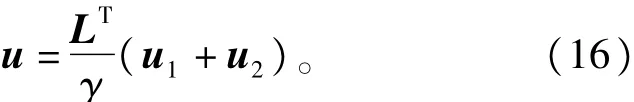
式中

其中u1表示基于超扭曲算法的高阶滑模控制项；u2表示含自适应参数的非线性控制项；表示k1、b1的估计值，b1、b2、k2、ρ、τ、γ为正实数，并满足表示矩阵LELT的最小特征值。

证明取Lyapunov函数

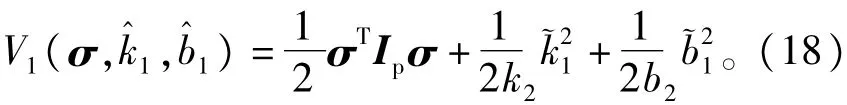
对式（18）求导可知

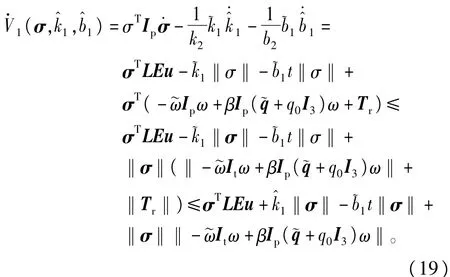
由0＜γ＜λ（LELT） 可知

min

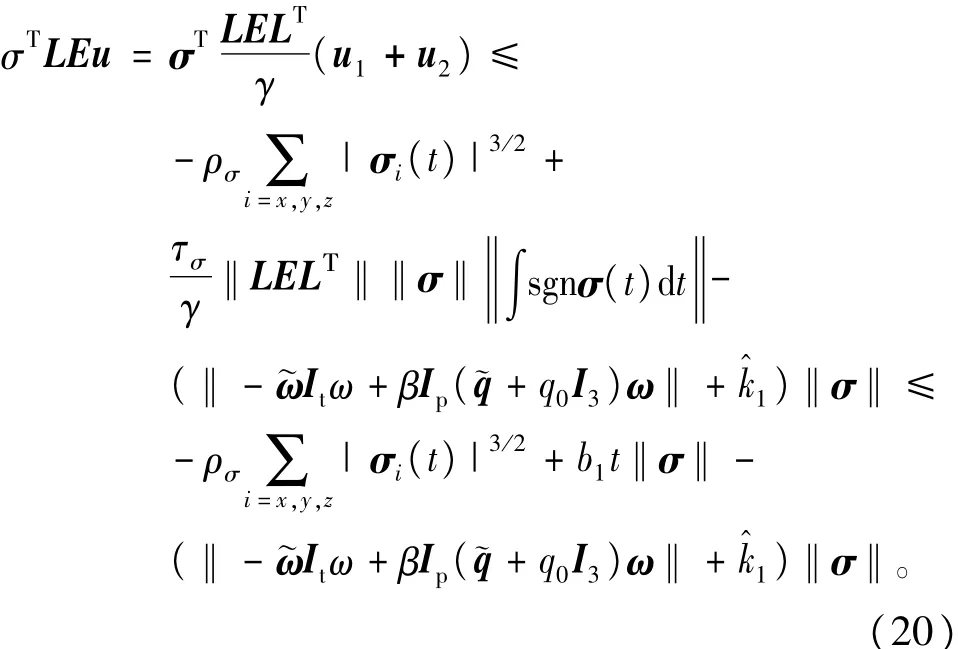
将式（20）带入式（19）可知

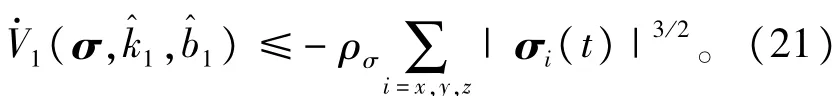
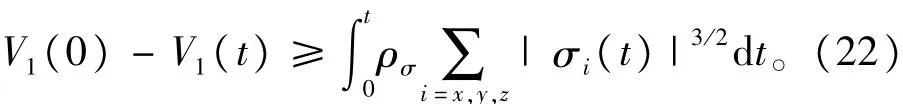
由于ρσ＞0，根据Barbalet引理，可知=0。

当σ=0时，ω=-βq，取Lyapunov函数V2（）=（1-q0）2+qTq，其导数满足

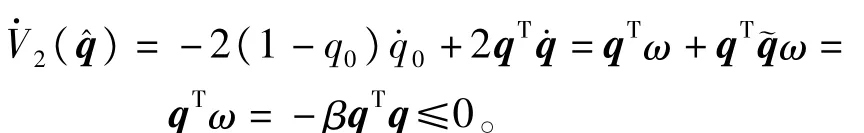
3 主动振动抑制补偿器设计

在容错控制器的作用下，有限时间内姿态角速度ω收敛到零，故可将ω及视为对挠性附件模态的微小扰动量。此时动力学方程（1）及（3）又可以表示为

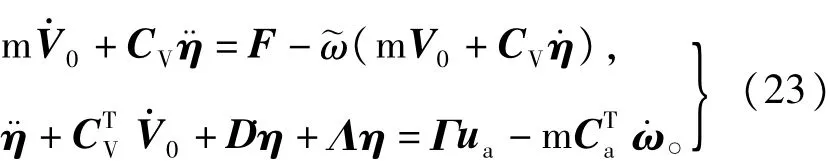
联立方程组（23），整理后可得

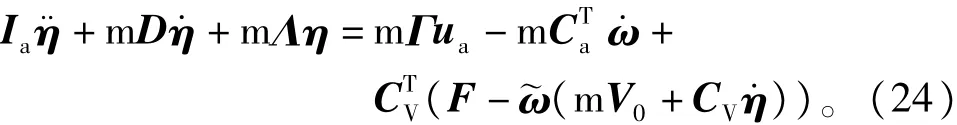
其中Ia=m I3-

考虑到高阶滑模在抖振和干扰抑制方面的优点，针对挠性振动方程（25），设计了基于超扭曲算法的高阶滑模主动振动抑制补偿器。步骤如下：

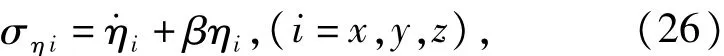
即ση=+βη。

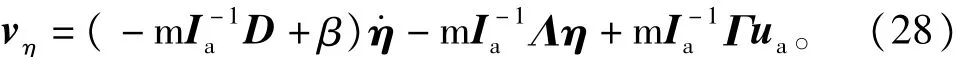
其中

根据引理可知，超扭曲算法必须满足干扰及其一阶导数有界的条件，因此作如下假设：

假设2扰动量ξη及其的一阶导数有界，并满足‖ξ‖≤k，‖‖≤k，其中k、k为未知正

η3434实数。

步骤3由假设2可知

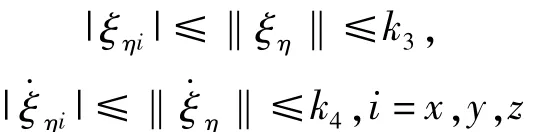
根据引理可知，当参数满足

时，则滑模变量σηi（t）和（t）在有限时间tηi≤7.6σηi（0）/（τηi-ρηi），（i=x，y，z）内收敛到零。

根据式（28）可知，实际控制量

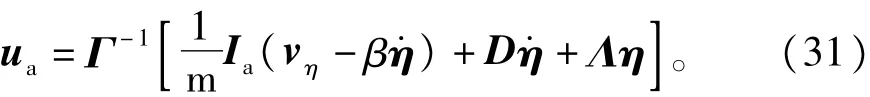
定理2在容错控制器对执行机构故障具有容错能力的前提下，若假设2成立，对于卫星的挠性附件振动模态方程（25），当控制参数满足β＞0、ρηi≥=x，y，z）并且τηi≥1.1k4，时，选取如式（31）描述的主动振动抑制控制律时，闭环控制系统（25）能在有限时间内稳定，挠性振动模态迅速收敛，并且满足=0。

证明由引理及步骤1～3的分析可知，对于系统（25），当主动振动抑制控制律（31）中的控制参数满足β＞0、ρη≥1.5（i=x，y，z）并且τη≥1.1k4（i=x，y，z）时，可知σ=+βη能在有限时间ηiitηi≤7.6σηi（0）/（τη-ρη）收敛到零。当ση=0时，=-βηi，进而满足=0。

4 仿真研究

为了验证所提出的高阶滑模容错控制器及主动振动抑制补偿器的作用效果，采用三正交+斜装的冗余飞轮配置，以轨控期间几种不同飞轮故障情形下的挠性卫星姿态控制系统为例进行了仿真实验。参数设置如下：

（1）卫星质量m=400 kg。

（2）卫星转动惯量

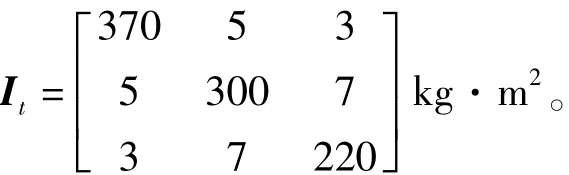
（3）星体平动与挠性附件振动的耦合系数

（4）星体转动与挠性附件振动的耦合系数

（5）主动振动控制元件与挠性附件间的耦合系数矩阵Γ=diag（［-0.023 4 0.004 22 -0.003 9］）。

（6）阻尼系数

（7）振动频率

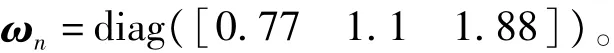
（8）轨道推力扰动F=［1 1 1］TN。

（9）反作用飞轮配置矩阵

（10）外界环境扰动

为了验证所容错控制算法的正确性及有效性，选取了以下执行器正常和故障两种情形进行了仿真实验。

情形1执行器正常，采用高阶滑模容错控制律式（16）、式（17）。

情形2执行机构存在完全失效，部分失效及恒值偏差故障，即

另外，为了体现所设计的高阶滑模容错控制器具有抑制抖振的优点，还将高阶滑模容错控制的效果与普通滑模容错控制的效果进行了仿真比较，见情形3。

情形3执行机构故障同情形2，采用普通滑模容错控制律（32）

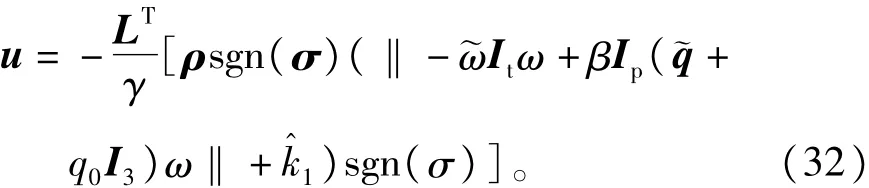
利用Matlab仿真软件，情形1下的控制效果如图1～图3所示。

从图1～图6中可以看出，在高阶滑模容错控制器及主动振动抑制补偿器的作用下，对于执行器正常和执行器故障这两种给定情形，闭环系统均能渐近稳定，并迅速收敛到期望值，姿态控制系统的状态量满足=0，从而证明了所设计的容错控制器和主动振动抑制补偿器的有效性和正确性。

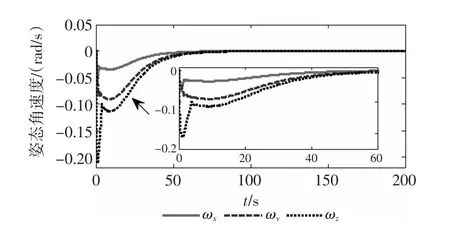
图2 姿态四元数响应曲线（情形1）Fig.2 Time response of attitude quaternion（case1）

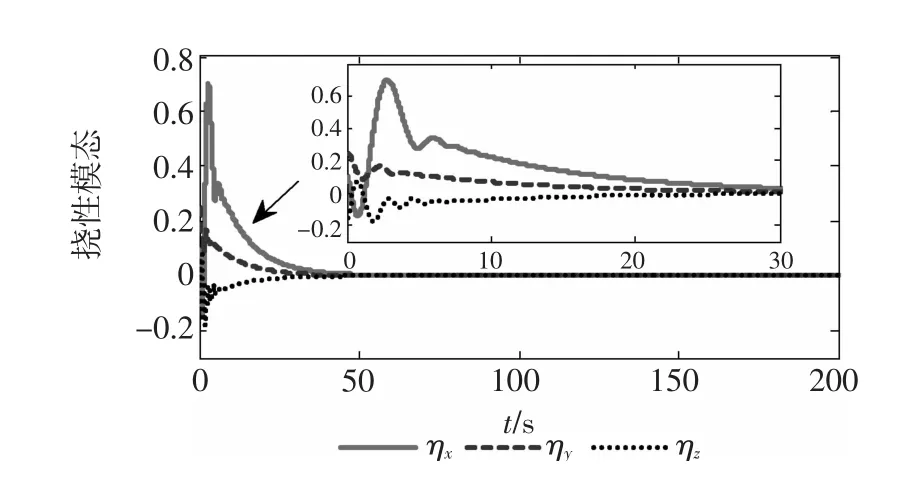
图3 挠性模态响应曲线（情形1）Fig.3 Time response of flexiblemodal（case1）

情形2下的控制效果如图4～图6所示。

情形3下的控制效果如图7～图8所示。

比较图7和图4、图8和图5，明显可以看出，虽然普通滑模容错控制方法也具备容错能力，但控制精度明显低于本文的高阶滑模容错控制方法。

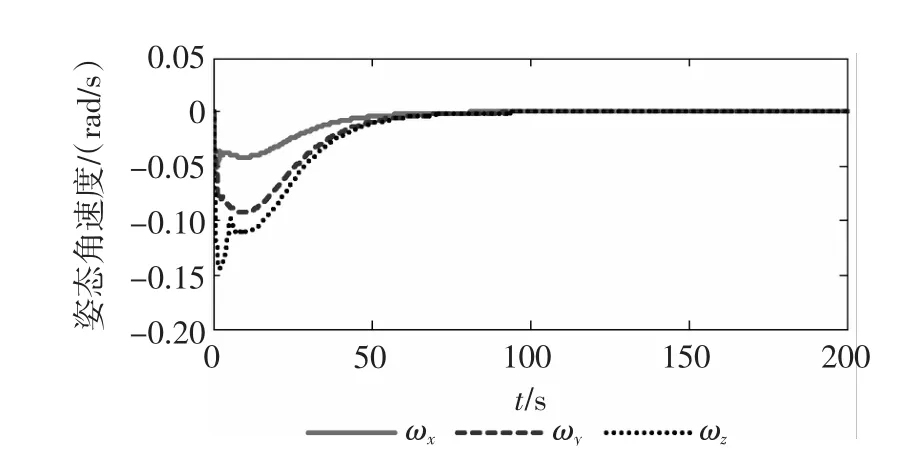
图4 姿态角速度响应曲线（情形2）Fig.4 Time response of attitude angu lar velocity（case2）

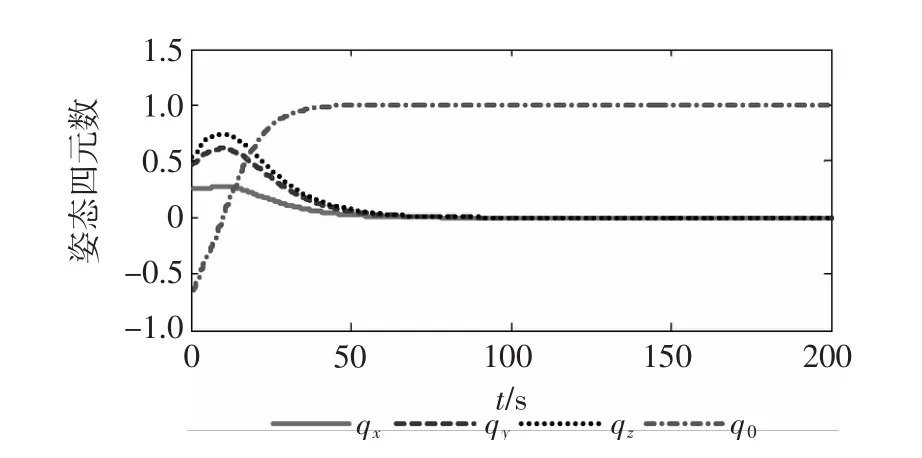
图5 姿态四元数响应曲线（情形2）Fig.5 Time response of attitude quaternion（case2）

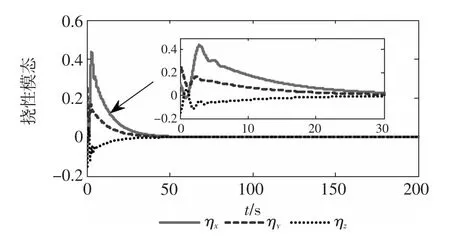
图6 挠性模态响应曲线（情形2）Fig.6 Time response of flexiblemodal（case2）

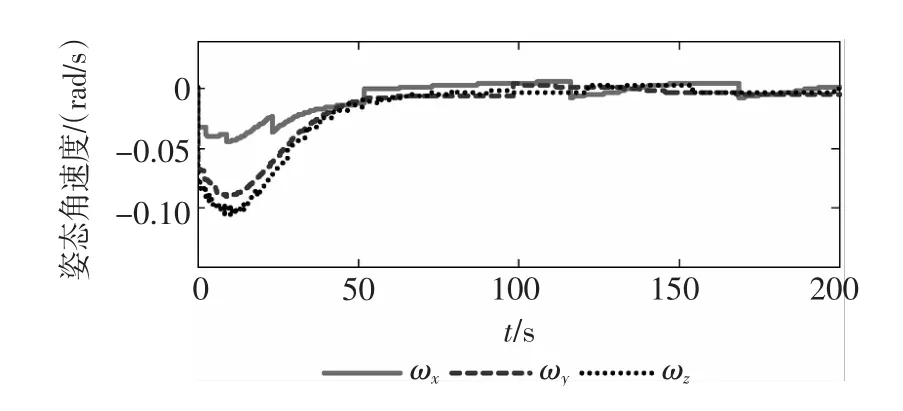
图7 姿态角速度响应曲线（情形3）Fig.7 Time response of attitude angular velocity（case3）

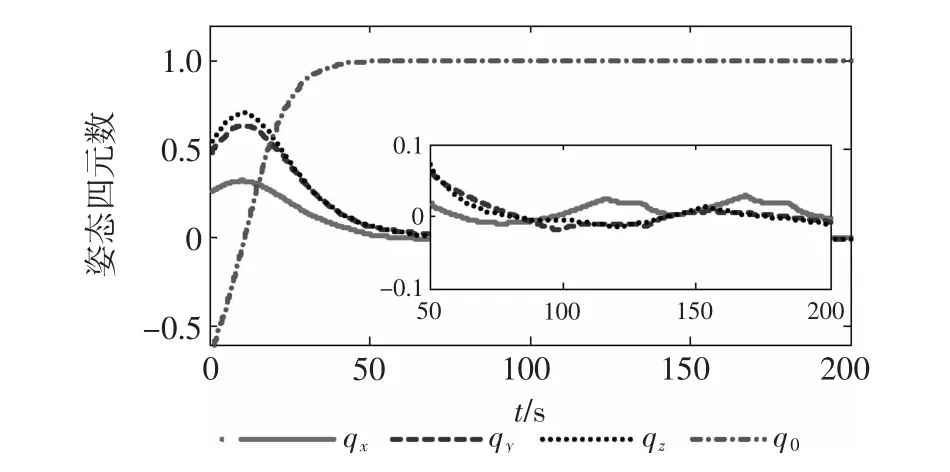
图8 普姿态四元数响应曲线（情形3）Fig.8 Time response of attitude quaternion（case3）

5 结 论

本文考虑轨道控制期间卫星姿态控制系统存在执行机构故障和轨道推力扰动的条件下，在采用‘三正交+斜装’冗余反作用飞轮结构配置的基础上，研究了一种基于高阶滑模容错控制及主动振动抑制问题。该算法在高阶滑模容错控制的基础上结合自适应控制，来达到容错控制的目的。进一步，在执行器具有容错能力的基础上，通过选取适当的辅助控制量及扰动量，构造了相应的微分方程组，从而将超扭曲算法运用到高阶滑模容错控制器及主动振动补偿器的设计中，并达到了本文期望的控制性能，避免了普通滑模算法中‘抖振’的负面影响。最后执行器正常及故障条件下的仿真结果及仿真对比结果验证了该容错控制器和主动振动抑制补偿器的正确性和可行性，说明该容错控制器具有良好的容错能力而且控制精度高于普通滑模容错控制器的作用效果。此外，本文方法不需要故障检测与诊断机构，因而实时性好。

［1］杨婧，史小平.卫星姿态系统的抗干扰完整性容错控制［J］.系统工程与电子技术，2013，35（1）：126-131.YANG Jing，SHIXiaoping.Integrity fault tolerant attitude controller of satellitewith disturbance attenuation［J］.Systems Engineering and Electronic，2013，35（1）：126-131.

［2］肖冰，胡庆雷，马广富.航天器执行机构部分失效故障的鲁棒容错控制［J］.控制与决策，2011，26（6）：801-805.XIAO Bing，HU Qinglei，Ma Guangfu.Robust fault tolerant attitude control for spacecraft under partial loss of actuator effectiveness［J］.Control and Decision，2011，26（6）：801-805.

［3］CHENG Yuehua，JIANG Bin，FU Yanping.Observer based reliable control for satellite attitude control systems with sensor fault ［J］.International Journal of Innovative Computing，Information＆amp；Control，2011，7（7B）：4149-4160.

［4］程月华，姜斌，孙俊，等.基于滑模观测器的卫星姿态控制系统滑模容错控制［J］.上海交通大学学报，2011，45（02）：190 -194.CHENG Yuehua，JIANG Bin，SUN Jun，et al.Sliding mode fault tolerant control for satellite attitude systems based on slidingmode observer［J］.Journal of Shanghai Jiaotong University，2011，45（02）：190-194.

［5］张娴，程月华，姜斌.轨控期间挠性卫星姿控系统的容错控制［J］.航天控制，2011，29（1）：41-47.ZHANG Xian，CHENG Yuehua，JIANG Bin.Adaptive backstepping fault-tolerant control for flexible satellite attitude control system during orbit control［J］.Aerospace Control，2011，29（1）：41-47.

［6］朱良宽，马广富，胡庆雷.挠性航天器鲁棒反步自适应姿态机动及主动振动抑制［J］.振动与冲击，2009，28（2）：132 -136.ZHU Liangkuan，MA Guangfu，HUQinglei.Attitudemaneuvering and vibration damping of flexible spacecraft via robust adaptive backstepping technique［J］.Journal of Vibration and Shock，2009，28（2）：132-136.

［7］HU Qinglei，MA Guangfu.Variable structure control and active vibration suppression of flexible spacecraft during attitudemaneuver［J］.Aerospace Science and Technology，2005，90：307-317.

［8］胡庆雷，马广富，姜野，等.三轴稳定挠性卫星姿态机动时变滑模变结构和主动振动抑制［J］.控制理论与应用，2009，26（2）：122-126.HU Qinglei，MA Guangfu，JIANG Ye，et al.Variable structure control with time varying sliding mode and vibration control for flexible satellite［J］.Control Theory＆amp；Applications.2009，26（2）：122-126.

［9］刘莹莹，周军.卫星轨道控制力对挠性帆板振动的影响［J］.西北工业大学学报，2009，27（1）：61-65.LIU Yingying，ZHOU Jun.Influence of satellite control force on its flexible solar panel during orbitmaneuver［J］.JournalofNorthwestern Polytechnical University，2009，27（1）：61-65.

［10］LIU Yingying，ZHOU Jun.Fuzzy attitude control for flexible satellite during orbitmaneuver［C］//The 2009 IEEE International Conference on Mechatronics and Automation，August 9-12，2009，Chang chun，China.2009：9-12.

［11］曾宪法，王洁瑶，王小虎，等.基于SMDO的滑模控制器设计及其在导弹上的应用［J］.航空学报，2011，35（5）：873 -880.ZENG Xianfa，WANG Jieyao，WANG Xiaohu，et al.Design of slidingmode controller based on SMDO and itsapplication tomissilecontrol［J］.Acta Aeronautica et Astronautica Sinica，2011，35（5）：873-880.

［12］李鹏.传统和高阶滑模控制研究及其应用［D］.长沙：国防科学技术大学研究生院，2011.

［13］马克茂.大型空间飞行器的高阶滑模姿态控制律设计［J］.控制与决策，2013，28（2）：201-210.MA Kemao.Design of higher order slidingmode attitude control laws large-scale Spacecraft［J］.Control and Decision，2013，28（2）：201-210.

［14］林壮，段广仁，宋申民.刚体航天器姿态跟踪的高阶滑模控制器设计［J］.控制与决策，2009，24（11）：1753-1756.LIN Zhuang，DUANGuangren，SONG Shenmin.Design of higher-order slidingmode controller for rigid spacecraft［J］.Control and Decision，2009，24（11）：1753-1756.

［15］Floquet T，PerruquettiW，Barbot JP.Angular velocity stabilization of a rigid body via vss control［J］.Journal of Dynamic Systems，Measurement and Control，2000，122（4）：669-673.

（编辑：刘素菊）

Fault tolerant control and vibration suppression of satellite attitude control system via higher-order sliding mode control

YANG Jing，SHIXiao-ping

（Control and Simulation Center，Harbin Institute of Technology，Harbin 150080，China）

A fault-tolerant controlwith active vibration suppression approach was proposed for the flexible satellite attitude control system with actuator faults during orbit control.Combined with adaptive control method，a higher-order slidingmode fault tolerant attitude controller was designed for the flexible spacecraftwith the orbit control force disturbance，and higher-order slidingmode compensator was designed to actively suppress the induced vibration.The simulation on the flexible satellite attitude system demonstrates that thismethod can achieve the actuator fault tolerance and improve the attitude control precision under the condition of interference.

higher-order slidingmode control；active vibration suppression；flexible satellite；fault tolerant control

10.15938/j.emc.2015.10.015

TP 302.8

A

1007-449X（2015）10-0100-07

2014-03-25

武器装备预研基金（9140A20040515HT01001）

杨 婧（1989—），女，博士研究生，研究方向为飞行器控制、容错控制；史小平（1965—），男，博士，教授，博士生导师，研究方向为飞行器智能控制、复杂系统仿真。

杨 婧