Boost变换器的抗扰动复合控制

徐媚媚，丁世宏，江浩斌

（1.江苏大学电气信息工程学院，江苏镇江212013；2.江苏大学汽车与交通工程学院，江苏镇江212013）

Boost变换器的抗扰动复合控制

徐媚媚1，丁世宏1，江浩斌2

（1.江苏大学电气信息工程学院，江苏镇江212013；2.江苏大学汽车与交通工程学院，江苏镇江212013）

为了探究Boost变换器中的扰动对升压的稳态和动态性能的影响，依据变PI（VAPI）控制理论和扰动观测理论提出了一种复合控制方案。首先，采用变PI控制方法设计状态反馈控制器，以提高Boost变换器的动态性能。其次，采用扰动观测器（DOB）观测Boost变换器中的扰动，从而得到扰动的估计值。最后，将该估计值作为前馈补偿到输入端，与变PI状态反馈相结合形成反馈加前馈的复合控制方案。仿真和实验表明，当存在输入电压突增、输入电压突降、负载突变等扰动时，与变PI控制相比，变PI+DOB的复合控制方案可以使得闭环系统具有更好的动态和稳态性能。

升压变换器；变PI控制；状态反馈；扰动观测器；复合控制

0 引 言

近年来，由于电力电子技术的发展，Boost型变换器广泛应用于各类直流升压场合如光伏发电、激光电源、电动与混合动力汽车以及新能源并网等领域。Boost变换器的主要作用是将低压直流电变为高压直流电，给负载提供稳定的直流电压。

值得注意的是，Boost变换器的数学模型存在非线性和非最小相位特性，这些性质给系统控制的设计带来很大不便。但是，也正是由于Boost变换器控制系统所具有的挑战性，吸引了国内外相关领域的广泛关注。目前国内外学者在Boost变换器方面也已经取得了很多研究成果，其控制方法获得了极大的发展，主要有包括.：双线性理论［1-3］、滑模变结构［4-6］、自适应方法［7-8］、鲁棒控制［9-10］和PID控制［11-12］等。文献［13］利用状态空间平均法分析电路并用PID调节器对电路进行了优化设计，但PID控制器的参数是恒定不变的，影响了调节时间和调节的效果。文献［14］提出一种改进型的PID控制，其参数根据电路的需要自动调节，缩减了调节时间且改善了系统的性能。文献［15］通过对系统进行线性化，再分析其近似的线性模型来得到控制规律。这些传统的线性化方法都是以泰勒展开式为基础的，利用这种方法所得到的模型是忽略了高阶非线性项的近似线性化模型，所以将其应用在非线性系统上存在很大的局限性。因此，非线性设计方法也开始引起大量研究者的关注。

文献［16］中推导出了Boost转换器状态反馈精确线性化模型，并在此基础上设计了滑模变结构控制器。该控制策略具有良好的动态响应调节和稳态误差调节特性，同时克服了现有精确反馈线性化控制策略固有的对精确数学模型依赖性的缺点，表现出更强的鲁棒性文献［17］提出一种新型Boost变换器非线性电流控制及其改进方法，该方法能够保证电感电流有效精确的跟踪给定值且控制系统动稳态性能良好。文献［18］中基于输入/输出反馈线性化提出一种新的非线性控制方案，该方案采用以非线性控制的电感电流作为内环、具有PI控制的电容电压作为外环的串级结构。它可以很好的解决以电容电压作为输出进行直接控制时所存在的不稳定零动态问题。

非线性控制器具有很强的鲁棒性，改善了线性控制器的缺陷，大大提高了系统的控制性能，使系统具有更好的控制品质。然而，一般情况下非线性控制器实现较为复杂，且成本较高，从而导致其在Boost变换器控制中未能广泛应用。相对而言，线性控制器因其结构简单、实现容易，且能够进行无差调节等特点在Boost变换器控制中被广泛采用。但是，对于线性控制器而言，其控制对象是简化后的线性系统，未能考虑原系统中的非线性和扰动等因素。若系统中的非线性因素或者扰动较大，线性控制对系统动态和稳态品质的改善能力有限。若保持系统的线性状态反馈控制器不变，设计扰动观测器对系统的非线性因素或者扰动进行观测，利用观测值进行前馈补偿，势必能够减小系统非线性和扰动对系统性能的影响。

基于此，在不改变现有线性反馈控制器情况下，本文利用扰动观测理论提出了一种改善系统性能的复合控制方法。此处，线性反馈控制器采用变PI控制器。基于线性扰动观测器实现对系统非线性和扰动的观测，并将观测值作为补偿量与变PI状态反馈控制器形成反馈加前馈的复合控制方案，从而达到改善系统性能的目的。与变PI控制相比，该方法具有干扰抑制能力强、响应快等优点。仿真和实验验证了该方法的有效性。

1 Boost电路的结构及建模

文中所考虑的电压型Boost变换器原理图如下：

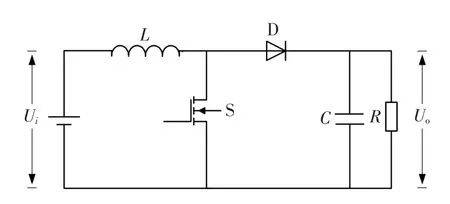
图1 Boost变换器原理图Fig.1 Principle diagram of the boost converter

图1由输入电源（Ui），电感（L），控制开关（S），二极管（D），电容（C）和负载（R）组成。电路工作时，存在两种形式的模态，即功率开关管导通与关断模态。其等效电路图如图2所示：由图2（a）知，当开关管S导通时，电感L为储能阶段，此时电源不向负载提供能量，负载靠储于电容C的能量维持工作。由图2（b）知，开关管S断开时，电源和电感共同向负载供电，同时电源给电容C充电。

图2 Boost变换器原理图Fig.2 Equivalent circuit of sw itch when open and close

利用不同状态等效电路，可以推导出每一模态的数学模型。由图2（a）得开关导通时数学模型为：

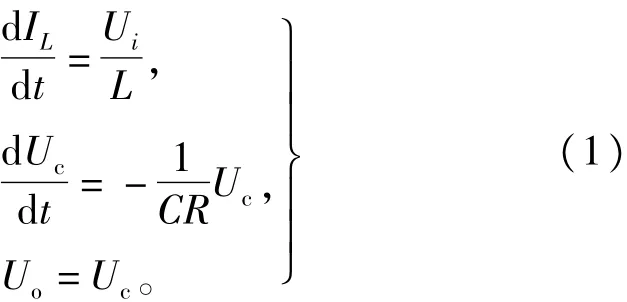
由式（1）可以得出相应的状态方程：

由图2（b）可得当开关闭合时的数学模型为：

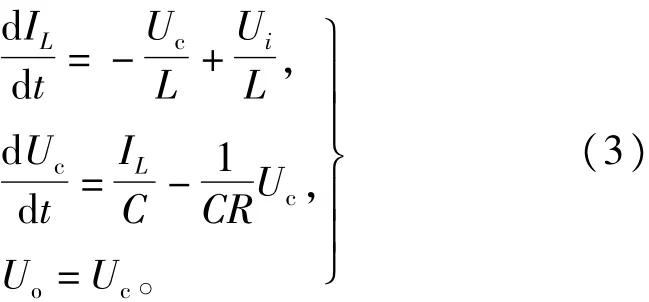
由式（3）可以得出相应的状态方程：

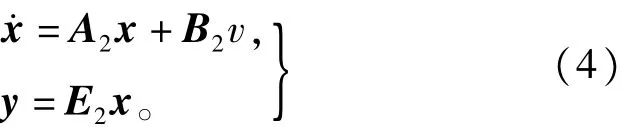
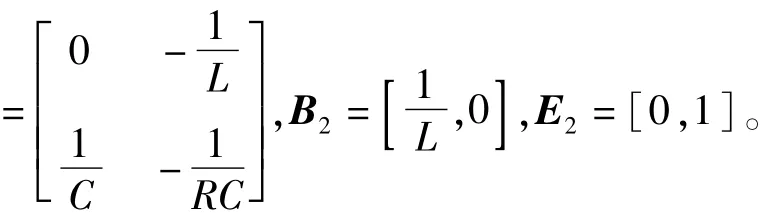
由于功率开关管的通断会引起一些变量的突变，因此要建立系统的状态空间平均模型。设状态变量x在一个开关周期内的值为＜x（t）＞Ts，经过平均化处理后的状态空间方程为［24］：

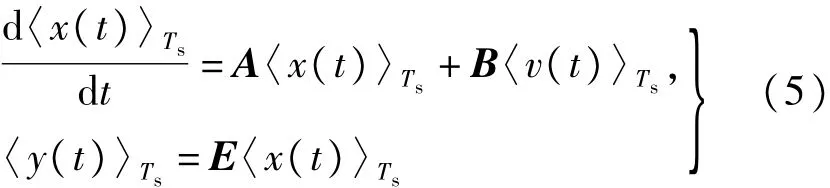
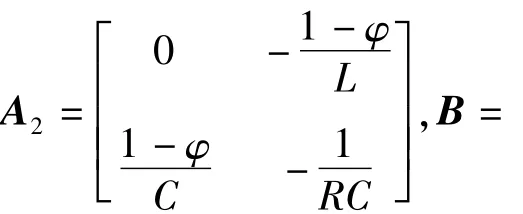
式中，X、V、Y分别表示为状态变量、输入电压、输出电压的稳态工作点矢量。由式（5）可以得到Boost变换器的稳态工作点为：

经计算可得：

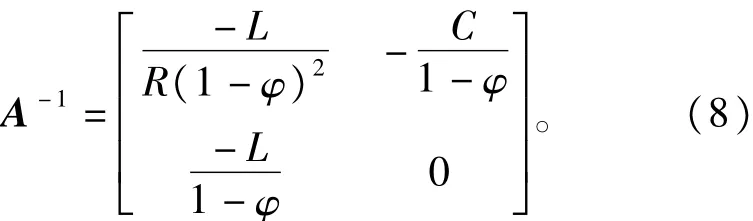
则

其中，D'=1-D，UI和D分别为输入电压和开关占空比在稳态时的值。

考虑到系统的非线性特性，故需要引入扰动。在稳定工作点附近引入扰动，其瞬时值为：

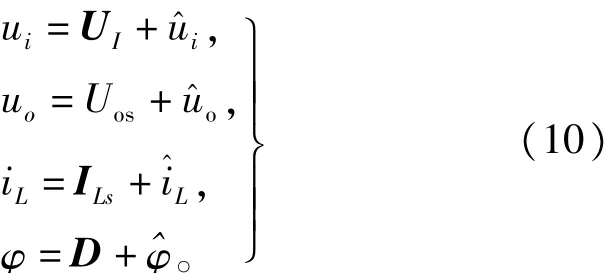
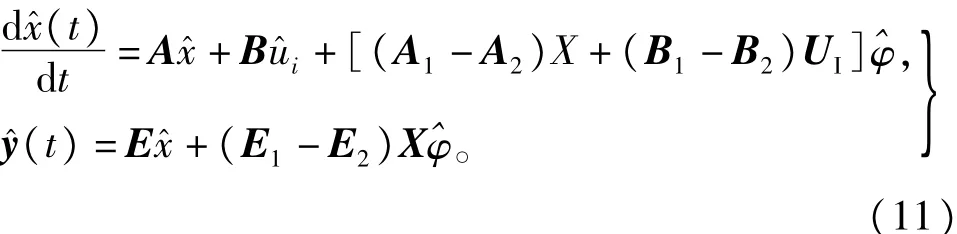
为了进一步分析Boost变换器的动态特性，对式（11）进行拉普拉斯变换，可以得到ˆφ（s）对uˆo（s）的小信号传递函数为：

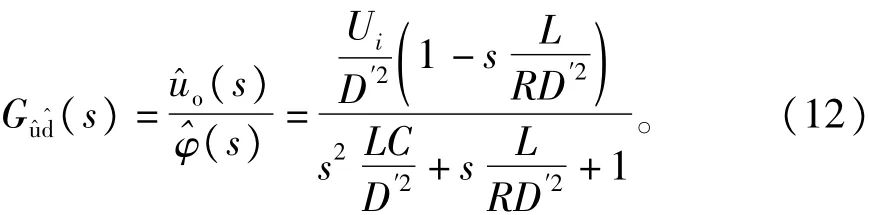
为了分析方便，将uˆo（s）/ˆφ（s）的传递函数简

化为

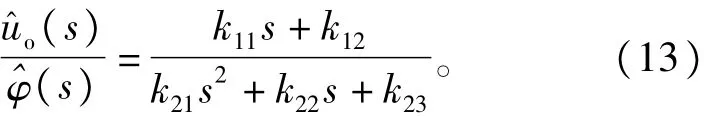
式中：k11=-UiL/RD'4，k12=Ui/D'2，k21=LC/D'2，k22= L/RD'2，k23=1。将其从频域方程转化为时域方程

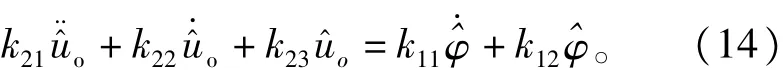
由于常数的导数为零，故式（14）可以化为：

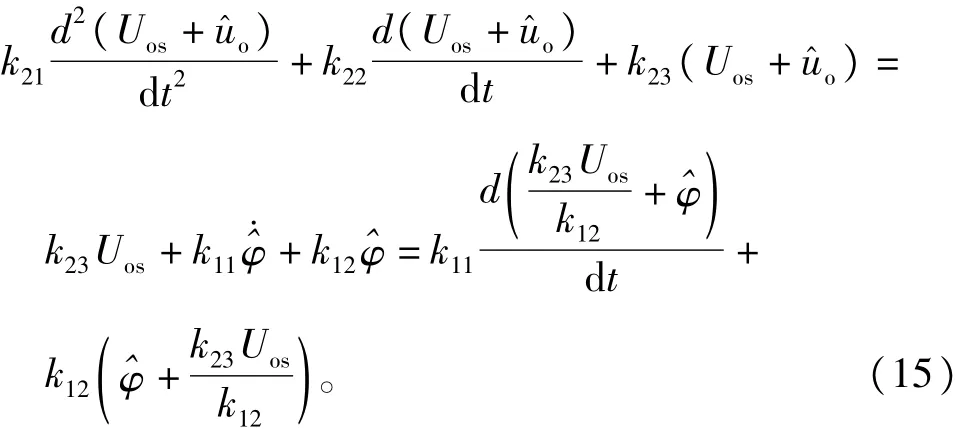
由式（10），再将时域方程转化回频域方程得：

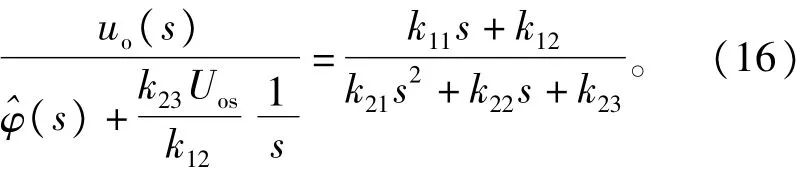
由于

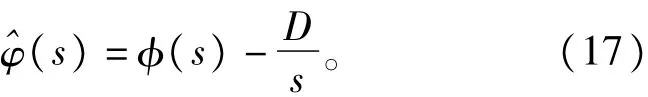
式（16）可以化为

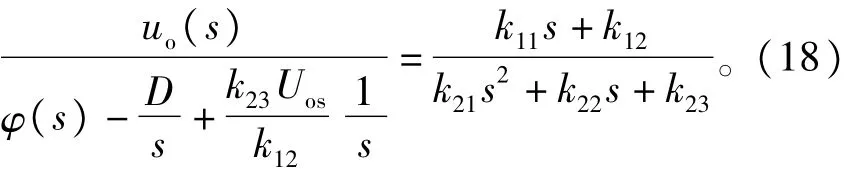
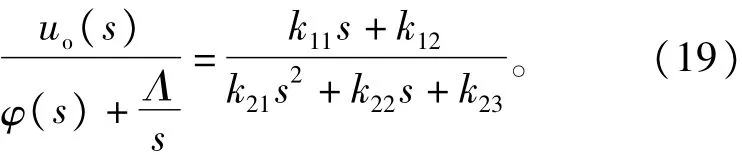
本文期望得到，但由于系统非最小相位，uo（s）/ˆφ（s）无法得到。通过式（19）可得

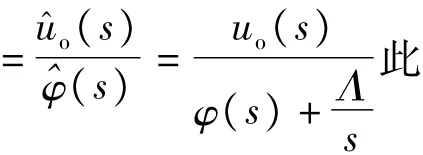
值得注意的是Guˆˆφ主要用来进行扰动观测器的设计，而扰动观测器不完全依赖系统的数学模型。

本文的控制目标为：在Boost变换器中，设计一个基于变PI+扰动观测的复合控制方案，使系统实际输出电压uo能够实现对参考电压uref的快速精确跟踪。

2 控制器设计

对于PWM型Boost变换器来说，工程中常见的控制器为PI（Proportional Integral）控制器。但一般情况下，PI控制器的参数是固定不变的。因此，很难适应系统的动态变化，故影响系统的控制性能。基于此，本节拟引入变参数PI（变PI）控制器，根据偏差的大小在线调节PI控制器参数，从而进一步提高系统的控制性能。此外，若系统中的非线性因素或扰动较大，则基于经典控制理论的PI控制对系统性能的改善程度有限，拟设计扰动观测器来对系统的非线性因素或者扰动进行观测，并对其进行补偿，以便减小它们对系统性能的影响。

2.1 变PI控制器

PI控制器的输出同时成比例地反应输入信号和输入信号的积分，传统PI控制器的控制规律在时域中可表示为

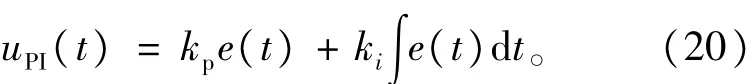
式中：uPI（t）为PI控制器的输出，e（t）为偏差信号，kp为比例增益，ki为积分增益。适当的整定PI控制器的两个系数kp和ki，可以使得系统满足一定的动静态性能。但是，传统的PI控制器中两个系数一旦确定后就不再改变，难以适应系统在多种复杂工况下的运行。另外，PI控制器参数的整定需要进行大量的实验，这给参数整定带来了较大的挑战。因此有必要对传统的PI控制器进行改进。

变PI控制方法是根据误差信号e的变化对PI控制器的比例和积分参数进行在线整定。当输入给定信号时，为了减小偏差和加快响应速度，需要增大kp值；当系统状态到达稳态附近时，为了系统的稳态性能，需要减小kp值。与此同时，积分系数ki在大偏差阶段会使系统响应的快速性变差，也会使系统出现较大的超调，所以ki在大偏差时应该取较小值；而在偏差e较小时，为保证系统稳态无静差，又不会引起积分饱和而使超调增大，ki应取较大值。基于此，我们可以取变PI控制器的增益函数为

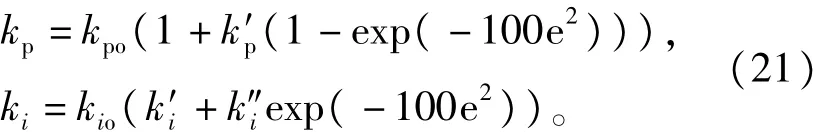
式中kpo，kio取常规PI控制整定的参数，和是修正系数，其中可在［0 Umax/（kpo-1）］中选取，一般可取可在［0 1］内取值，而在［1+∞］上取值。据此得到变PI控制的方程：

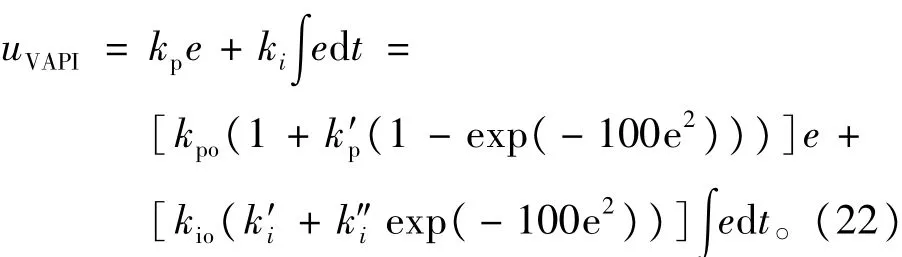
由于变PI控制器优点明显，我们利用变PI控制技术设计Boost变换器控制系统的反馈控制器，具体框图如下。

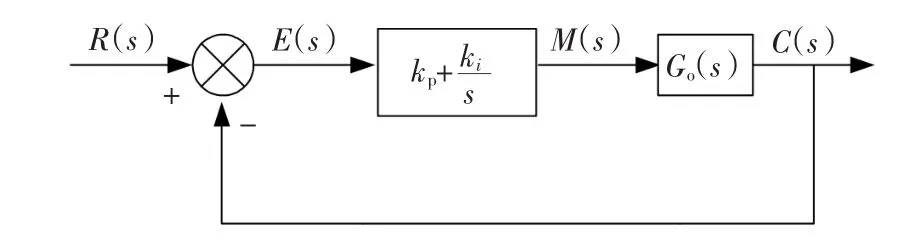
图3 变PI控制框图Fig.3 Block diagram of variable parameter PI control

3 扰动观测器设计

扰动观测器的主要原理是将实际的系统输出与参考模型输出的差异看作一个等效的干扰加入到输入端，在控制量中引入相应的补偿，实现对干扰的完全抑制。由于讨论的Boost变换器属于非最小相位，若采用传统的思想构建扰动观测器，则Boost变换器传递函数中的零点将会变成扰动观测器中的极点，从而使得观测器不稳定，无法有效观测出扰动值。扰动观测器的非最小相位结构图为：

图4 扰动观测器结构图Fig.4 Block diagram of disturbance observer

其中G（s）为实际被控对象，Gn（s）为标称模型，（s）为重构的系统模型的逆，u为参考输入，d为r外部干扰，δ为等效补偿项。将ur，d作为输入信号，求得输出δ的表达式为：

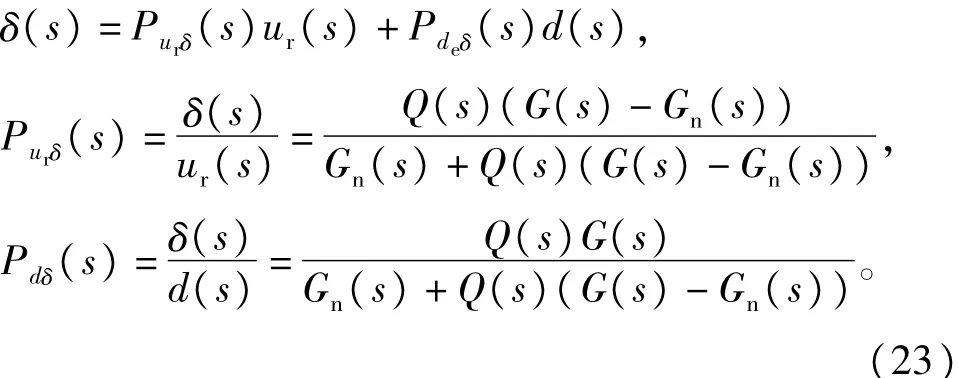
对标称模型进行分解来解决非最小相位问题。将Gn（s）分解为如下形式：

式中：

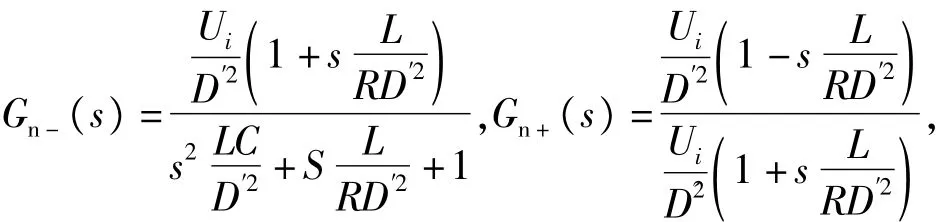
由式（23）可知，假定实际被控对象为标称模型，且不存在外部干扰（即d=0），则补偿项δ为0。这说明DOB只有在干扰激励下才会发挥控制作用，并不是一直参与系统的控制。

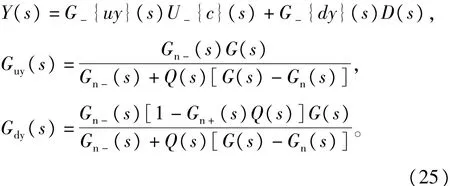
在设计扰动观测器时，我们期望得到uo（s）转换到时域中，也就是实际得到的值比期望值多了个常数量Λ（详细情况见第1节的最后部分）。因此，在观测器设计中，我们可以引入一个外部补偿环节。基于此，扰动观测器结构图可以进一步改写为：

扰动观测器的设计取决于Gn（s）和Q（s）的选择。文献［22-23］提出了一种Q（s）的表达式：

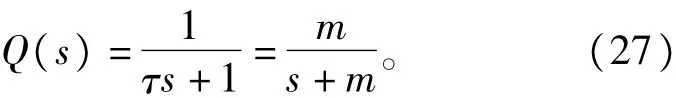
其中：m=1/τ。

图5 扰动观测器改进结构图Fig.5 Block diagram of improved disturbance observer

综上可以得到系统控制方案如下：控制器由基于变PI的反馈项和基于扰动观测器的前馈项组成。反馈项用来消除误差，而前馈项用来进行扰动补偿，改善系统的性能。

4 仿真及分析

为了验证本文所设计的控制算法的可行性和正确性，在Matlab中SIMULINK环境下进行了仿真研究。仿真参数设定为输入电压为8 V，电感为4mL，电容为30mF，负载电阻为10Ω，=0.5，kio=0.1=1。当输入电压为8 V时，设定输出电压的期望值为12 V，在SIMULINK环境下进行仿真验证。不外加扰动的条件下，PI控制器，变PI控制器，变PI+DOB控制器的效果图如图6所示。

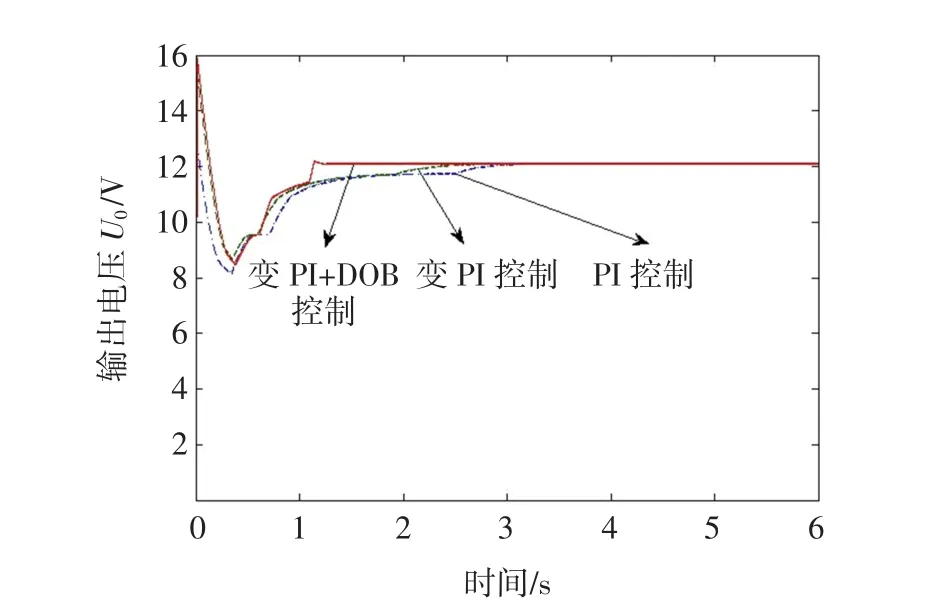
图6 无外加扰动时变控制效果图Fig.6 Simulation results in the absence of disturbance

由图6可知，在无外加扰动的情况下，PI控制，变PI控制和变PI+DOB控制均具有良好的动态及稳态响应，变PI控制略优于PI控制且变PI+DOB控制稳态精度略优于变PI控制。

设定在进入稳态后，Boost变换器输入电压从8 V突增到10 V，PI控制，变PI控制和变PI+DOB控制效果对比图如图7所示。

图7 输入电压突增时变控制效果图Fig.7 Simulation results under input voltage surge

由图7可知，当输入电压突增时，引起了输出电压的一定幅度的增大，相对PI控制而言，变PI和变PI+DOB控制能更快进入稳态且变PI+DOB控制性能优于变PI控制。

设定在进入稳态后，输入电压从8 V突降到6 V，PI控制，变PI控制和变PI+DOB控制效果对比图如图8：由图8可知，当输入电压突降时，引起了输出电压的一定幅度降低，相对PI控制而言，变PI控制和变PI+DOB控制进入稳态时的调节时间更短且变PI+DOB控制性能优于变PI控制。

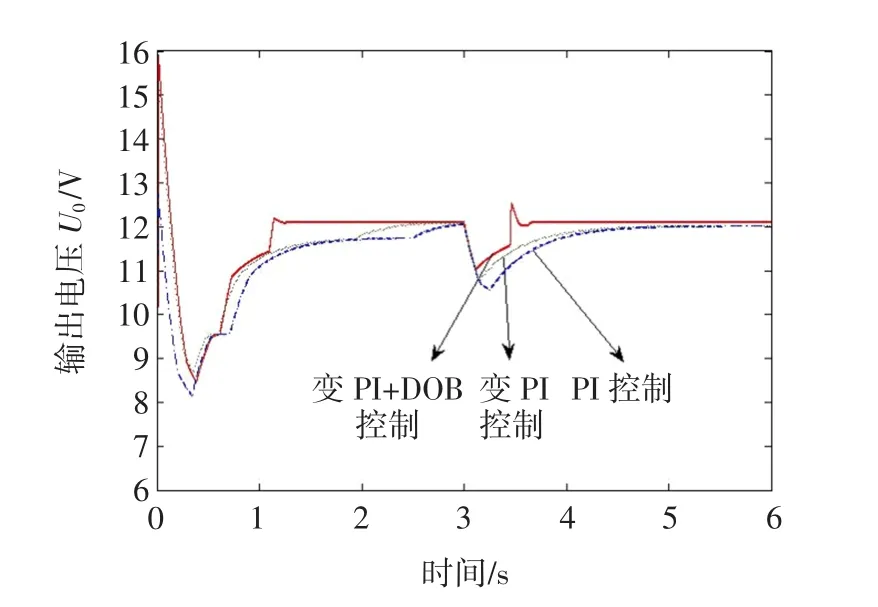
图8 输入电压突降时控制效果图Fig.8 Simulation results under input voltage dip

设定在进入稳态后，负载电阻从50Ω突变为220Ω时，PI控制，变PI控制和变PI+DOB控制效果对比图如图9所示。

由图9知，当输入电阻突升时，引起输出电压的升高，但变PI+DOB控制能以较快的速度进入稳态，相对于变PI控制和PI控制而言，性能更优。

由上述仿真图可以看出：这三种控制方案的主要差别是在加入扰动时的动态性能的差异。在无外加扰动时，PI控制，变PI控制和变PI+DOB的控制效果相近，但是在外加了扰动（输入电压突增2 V、输入电压突降2 V和负载电阻突变）后，变PI+DOB控制恢复到稳态时的时间明显短于变PI控制和PI控制。因此，变PI的抗干扰性能更强。

5 实验及分析

本实验中测试仪器分为硬件和软件两个部分。软件部分是以labview（Laboratory Virtual Instrument Workbench）软件为平台设计了一种应用在Boost变换器上的变PI与DOB相结合的复合控制算法。

整个硬件部分主要由采集卡和Boost底层电路构成。下面是实验的设备图：底层Boost电路是以电压型PWM控制器TL494为核心的稳压输出开关电源。电路原理图如图10：

图10 实验设备图Fig.10 Laboratory equipment figure

图11中电阻R0、瓷片电容C2分别起到分流和滤波的作用。TL494是一种固定频率脉宽调制电路且内置线性锯齿波振荡器、误差放大器和5 V参考基准电压源，外置震荡元件。通过选择控制算法来控制TL494的3引脚从而控制PWM的占空比来得到期望的输出电压。选取的电路元件参数为：C0= 22 pF，C1=220μF，C2=4.7μF，R0=10 kΩ，L= 330μH，R1=1 000Ω，R2=220Ω，R3=100 kΩ，R4= 20 kΩ，Ui=8 V，T=0.001 s，开关频率为20 kHz。低通滤波器截止频率为1 000 Hz，即Q（s）=1 000/s+ 1 000。通过计算可得

图11 电压型Boost变化器原理图Fig.11 Principle diagram of voltage type Boost converter

D=1/3，Λ=k23Uos/k12-D=1/3，由式（12）带入相关参数可以得到Guˆdˆ（s）的表达式，如下

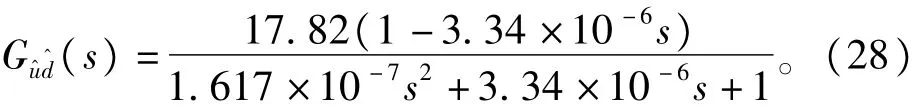
在经过多次参数的调试，最终PI控制变PI控制的参数kp和ki确定为2.0和0.01。

当输入电压为8 V，设定输出电压的期望值为12 V，不外加扰动的条件下，PI控制器，变PI控制器和变PI+DOB控制器的实验图如图12所示。

图12 无外加扰动实验图Fig.12 Experiment result in the absence of disturbance

在输入电压由8V突升到10V，PI控制器，变PI控制器和变PI+DOB控制器的实验图如如图13所示。

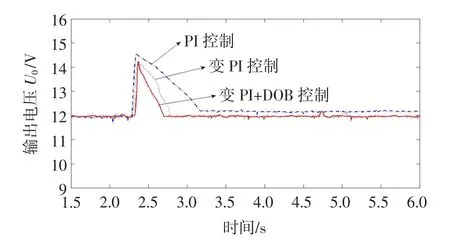
图13 突增电压实验图Fig.13 Experim ent result under input voltage surge

在输入电压由10V突降到8V，PI控制器，变PI控制器和变PI+DOB控制器的实验图如如图14所示。

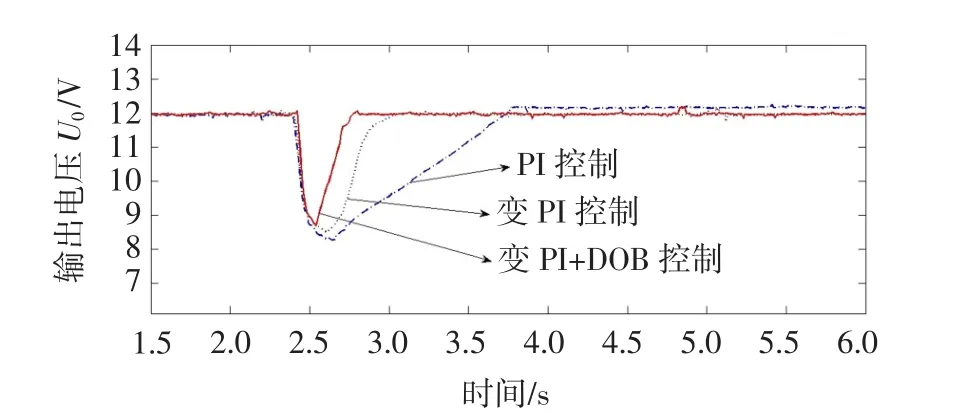
图14 突降电压实验图Fig.14 Experiment result under input voltage dip

负载由50Ω突变为220Ω时，PI控制器，变PI控制器和变PI加DOB控制器的实验图如图15所示。

图15 突变电阻实验图Fig.15 Experiment result under load resistancemutation

从上述实验来看，实验结果与仿真相吻合。可以看出变PI+DOB控制的收敛时间明显小于变PI控制和PI控制，控制效果优于变PI控制和PI控制。在外加了干扰（突增电压、突降电压和突变电阻）的情况下，DOB发挥了作用，减短了收敛时间，提高了系统的控制性能。

6 结 论

针对Boost变换器中应用变PI+DOB的控制算法的情况进行了较全面的分析。该方法在变PI控制设计中引入扰动观测技术，可以大大提高Boost变换器的动态性能且对外部有着很强的鲁棒性。理论分析、电路仿真及实验均证实了所提变PI+DOB控制方案的有效性。

［1］BAEK J，PARK M.Fuzzy bilinear state feedback control design based on TS fuzzy bilinearmodel for DC-DC converters［J］.International Journal of Electrical Power and Energy Systems，2012，42（1）：710-720.

［2］NAOYA K，HIROSHIN，MASAMIM.A new control law of bilinear DC-DC converters developed by direct application of lyapunov［J］.IEEE Transactions on Power Electronics，1995，10（3）：318-325.

［3］CARLOSO，ISABELLEQ，RAMON L，etal.Optimal state-feedback control of bilinear DC-DC converterswith guaranteed regions of stability［J］.IEEE Transactions on Industrial Electronics，2012，59（10）：3868-3880.

［4］MAGNUS H，JANAÍNA O G.Sliding mode 4-quadrant DCDC converter for a flywheel application Hans［J］.Control Engineering Practice，2013，21（4）：473-482.

［5］YAN Z，HONG,EN L，SHAN L.Finite-time control of boost converter via backstepping slidingmodemethod［J］.Journal of Computational Information Systems，2013，9（19）：7815-7822.

［6］NAOUARBEN M W，HANIA B，SLAMA I，et al.FPGA-based slidingmode direct control of single phase PWM boost rectifier ［J］.Mathematics and Computers in Simulation，2013（91）：249 -261.

［7］TONIB，ZELJKO B，NEDJELJKO P.Adaptive control of peak currentmode controlled boost converter supplied by fuel cell［J］.Journal of Power Electronics，2013，13（1）：122-138.

［8］CAROLINA A，FRANCISCO G，CARLOSCW.Adaptive control design for a boost inverter［J］.Control Engineering Practice，2011，19（1）：32-44.

［9］OLALLA C，LEYVA R，AROUDIA El，etal.LMI robust control design for boost PWM converters［J］.IET Power Electronics，2010，3（1）：75-85.

［10］WANG Y X，YU D H，KIM Y B.Robust time-delay control for the DC-DC boost converter［J］.IEEE Transactions on Industrial Electronics，2014，61（9）：4829-4837.

［11］MUMMADIV.Design of robust digital PID controller for H-bridge soft-switching boost converter［J］.IEEE Transactions on Industrial Electronics，2011，58（7）：2883-2897.

［12］HWU K I，YAU Y T.Performance enhancement of boost converter based on PID controller plus linear-to-nonlinear translator ［J］.IEEE Transactions on Power Electronics，2010，25（5）：1351-1361.

［13］朱鹏程，郭卫农，陈坚.升压斩波电路PI和PID调节器的优化设计［J］.电力电子技术，2001，35（4）：28-31.ZHU Pengcheng，GUOWeinong，CHEN Jian.Optimum design of PIand PID regulator for the boost chopping circuit［J］.Power Electronics，2001，35（4）：28-31.

［14］SHEN Z，YAN N，MIN H.A multimode digitally controlled boost converter with PID autotuning and constant frequency constant off-time hybrid PWM Control［J］.IEEE Transactions on Power Electronics，2011，26（9）：2588-2598.

［15］TAN FD，RAMSHAW R S.Instabilities ofa boost converter system under large parameter variations［J］.IEEE Transactions on Power Electronics，1989，4（4）：442-448.

［16］乐江源，谢运祥，洪庆祖，等.Boost变换器精确反馈线性化滑模变结构控制［J］.中国电机工程学报，2011，31（30）：16 -23.LE Jiangyuan，XIE Yunxiang，HONG Qingzu，et al.Sliding mode control of boost converter based on exact feedback linearization［J］.Proceedings of the CSEE，2011，31（30）：16-23.

［17］帅定新，谢运祥，王晓刚，等.Boost变换器非线性电流控制方法［J］.中国电机工程学报，2009，29（15）：15-21.SHUAIDingxin，XIE Yunxiang，WANG Xiaogang etal.Nonlinear current controlmethod for boost converter［J］.Proceedings of the CSEE，2009，29（15）：15-21.

［18］刘景波，明文龙.一种基于输入/输出反馈线性化的Boost型DC/DC变换器非线性控制方案［J］.中国电机工程学报，2010，30（27）：55-61.LIU Jingbo，MINGWenlong.A novel scheme ofnonlinear control strategy based on input-output Linearization for Boost type DC/DC converter［J］.Proceedings of the CSEE，2010，30（27）：55-61.

［19］武琳，刘志刚，洪祥.隔离式双向全桥DC-DC变换器的功率控制特性比较与分析 ［J］.电工技术学报，2013，28（10）：179-187.WU Lin，LIU Zhigang，HONG Xiang.Comparison and analysis of power control characteristic for isolated bidirectional full-bridge DC-DC converter［J］.Transactionsof China Electrotechnical Society，2013，28（10）：179-187.

［20］钟庆昌，谢剑英，李辉.变参数PID控制器［J］.信息与控制，1999，28（4）：273-277.ZHONG Qingchang，XIE Jianying，LIHui.PID controlwith variable argum ents［J］.Information and Control，1999，28（4）：273-277.

［21］CHOIY，YANG K，CHUNG KW et al.On the robustness and performance of disturbance observer for second-order systems［J］.IEEE Transtrons on automatic control，2003，48（2）：315 -320.

［22］SEONG L H.Robust digital tracking control lers for high-speed/high-accuracy positioning systems［D］.Berkeley，USA：University of California，1994.

［23］KARATYGIN SA，PANFILOV D I.Analysis of the characteristics of pulse voltage regulators using the state-space averaging method［J］.Soviet electrical engineering，1988，59（12）：81 -87.

（编辑：贾志超）

Boost converter disturbance resistant com posite control

XU Mei-mei1，DING Shi-hong1，JIANG Hao-bin2

（1.School of Electrical and Information Engineering，Jiangsu University，Zhenjiang 212013，China；2.School of Automotive and Traffic Engineering，Jiangsu University，Zhenjiang 212013，China）

In order to explore the disturbance effect on the dynamical and steady performance of a boost converter.A composite control strategy was proposed by combining the variable parameter PI（VAPI）control theory and disturbance observation theory.First of all，the VAPI controller was designed to improve the dynamic performance of the Boost converter.Then，the disturbance observerwas adopted to estimate the disturbance of the Boost converter，and thus the estimated value of disturbance was obtained.Finally，taking the estimated value as the forward compensation，combined with the feedback VAPI controller，a composite control scheme was obtained.Simulation and experiments show that compared with VAPI controller，the composite controller ensuresmuch better dynamical and steady behavior in the presence of input voltage surge，input voltage dip and load mutation.

Boost converter；variable parameter PI control；state feedback；disturbance observer；composite control

10.15938/j.emc.2015.10.005

TM 46

A

1007-449X（2015）10-0030-08

2014-11-06

国家自然科学基金（61203014，61273142）；江苏省高校优势学科建设工程资助项目（PAPD，苏政办发（2011）6号）；中国博士后基金（2015M571687）；江苏省自然科学基金（BK2012283）

徐媚媚（1991—），女，博士研究生，研究方向为基于扰动观测的Boost电路复合控制；丁世宏（1983—），男，博士，副教授，研究方向为滑模控制理论和功率变换器控制；江浩斌（1969—），男，博士，教授，研究方向为车辆系统动力学与控制技术。

丁世宏