图像预处理对人脸识别系统性能影响研究

2015-01-05文成玉

成都信息工程大学学报 2015年1期

金欣，文成玉，杜鸿

(成都信息工程学院通信工程学院，四川成都610225)

0 引言

从Lades等[1]首次提出将主成分分析法(Principal Component Analysis，PCA)应用于人脸识别之后，子空间法就得到极大的关注，子空间法的优势在于它通过空间的变换，将线性的或者非线性的图像特征进行压缩，从高维空间降维至低维的特征子空间，从而降低算法的复杂度。到目前为止，基于PCA的特征脸算法(Eigenface)有了深远的发展且已经趋于成熟，并延伸出其他的变种算法，最有代表性的就是 Belhumeur提出的 Fisherface算法[2]，是将线性鉴别分析理论[3](Linear Discriminant Analysis，LDA)与 PCA 相结合，将经过PCA降维后的表观特征的主成分，采用LDA进行变换，使系统可以获得尽量大的类间散度和尽量小的类内散度。这两种识别算法是目前较为主流的基于子空间的人脸识别算法[4]。现今，多数可以实现工程化的人脸识别系统仍是基于子空间算法的，想要得到一个具有非常高识别率的系统，已经不能单纯的只改进算法的原理，从获取到的人脸图像的源头进行预处理，才是提高一个识别系统识别率非常重要的环节。

根据山世光教授[5]提到的人脸识别系统中存在的若干问题，一个强壮的人脸识别系统对于人脸库和输入到系统的待识别图像会有不同的要求，例如一个庞大的人脸库会对识别的效率和算法复杂度产生高要求，有时为了降低识别计算的时间，在算法原理上无法得到改进的情况下，就会在获取图像时就对图像进行像素和尺寸的降低，像素降低的优势在于可以同时减小人脸库的存储空间，在实际应用中，有非常大的工程实用性。图像预处理往往只有短短几行代码，却能实现极大的改善一个系统的识别率，下面将从分析子空间算法的类间距离和类内距离入手，通过加入预处理，使其作用于图像的类，分析其类的变化加以判断Eigenface和Fisherface所需要的预处理方法。

1 图像预处理技术方法

人脸图像的预处理的目的是使不同成像条件下拍摄的所有进入识别系统的照片具有一致性。后续将重点介绍几何归一化中的图像掩模技术[6]和图像增强中的直方图均衡[7]，并且加入可以去除噪声的维纳滤波法[8]。

1.1 图像掩模

一般获取的图像都存在干扰信息，图像掩模为了解决这种负面的影响，抠出主要的人脸部分。具体的基本步骤就是首先将人脸图像进行几何校正处理，就是将人脸图像实施人像扶正，根据标定的人眼坐标进行图像缩放和图像切割等操作后，然后产生一个固定的矩形模板，该模板的中心有个与人脸大小大致相同的椭圆区域，其内部的值都为1，椭圆区域以外的值都为0，模板的大小与人脸图像大小相同，其次，人眼在校正过的人脸图像中位置固定，且中心轴对称，将两个图像矩阵相与计算，就会得到经过掩模后的图像。

1.2 直方图均衡

由于子空间算法对于光照的鲁棒性非常低，这也是解决影响子空间算法识别率一大问题的主要方法。在人脸识别的过程中，增加灰度对比度可以突出人脸重要的特征。

直方图均衡化是通过改变每个灰度级上像素点分布，使其都具有相同的象素点数，目的是使图像在整个灰度值动态变化范围内分布均匀化，改善图像的亮度分布状态，增强图像的视觉效果。均衡化的原理是根据熵理论[9]，可知当 H(0)，H(1)…，H(n－1)相等时，图像信息量最大。

1.3 维纳滤波

图像在采集的过程中难免会产生噪声，维纳滤波的优势在于适应面较广，无论平稳随机过程是离散还是连续，标量还是向量。在一个线性系统中，输入的随机信号x(n)，输出为y(n)，在x(n)中包含信号s(n)和噪声v(n)，当x(n)通过线性系统h(n)后得到的y(n)尽量接近于s(n)，用^s(n)表示估计值，维纳滤波是从过去的观察值估计过去的信号值y()n=^s(n+N)(N≥1)。维纳滤波常被称为最佳线性过滤预测或线性最优估计[10]，因其是以最小均方误差为准则的。

2 子空间算法的图像差值模型

从最近邻法分类[11](Nearest Neighbor，NN)的角度出发，人脸图像差值分为两类:人脸的类内差值△I(intra-class difference)和人脸的类间差值△E(extraclass difference)。

2.1 Eigenface的类内类间距离模型

设N个模式样本{χl}分属c类，记为ωi=，i=1，2，…，c，则ωi类模式的样本均值矢量为各类模式的样本总体均值矢量为

C 类的样本均值矢量为m(i)，则类内均方欧式距离[12]为

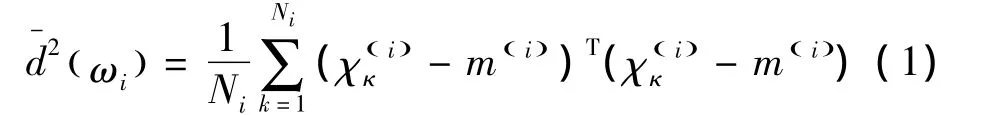
2.2 Fisherface的类内类间散度模型

Fisherface对数据首先采用PCA进行降维处理，计算PCA投影子空间WPCA，求出空间的类内平均图像mi及总的平均图像m。随后计算第i类的类内散布矩阵Si和总的类内散布矩阵Sw，公式如下

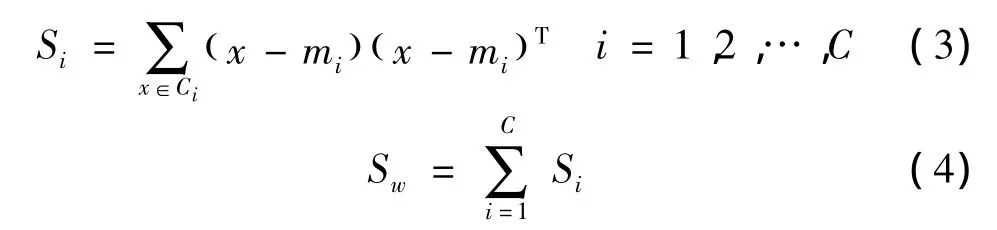
计算类间散布矩阵

通过降维可以保证类内离散度矩阵的非奇异性[13]。然后根据散度差准则求解目标函数[14]。

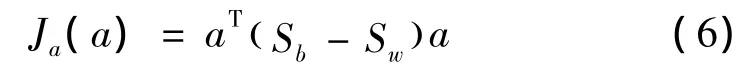
其中，a为Sb－Sw的最大特征值对应的单位特征矢量。

3 Matlab仿真实验

实验采用美国FERET人脸库[15]，总共采集200人的人脸信息，每人7幅图像，总共1400幅人脸图像作实验人脸库。原始人脸库中的像素尺寸为80×80，在此基础上将像素尺寸缩小成40×40的人脸库，形成高像素人脸模型和低像素人脸模型。下面将深入研究图像掩模、直方图均衡和维纳滤波对于类的差值影响。

图1 图像预处理效果图

图1展示了原始图像经过了不同预处理后的效果，图1(a)是原始人脸图像，图1(b)、(c)、(d)三幅图像依次是经过图像掩模、直方图均衡和维纳滤波后的效果图，图1(e)图展示了直方图均衡和维纳滤波叠加效果，而图1(f)图像则是3种预处理方法叠加的真实效果图。直观上可以看出，直方图均衡可以提高图像对光照的鲁棒性，维纳滤波可以去除噪声的干扰，而掩模则彻底排除了一切与背景无关信息量的干扰，这种对于图像的改善从一定程度上提高了人脸识别系统对于光照和采集环境的鲁棒性，从而在一定程度上提高了系统抗干扰能力。

3.1 Eigenface的仿真实验

根据Eigenface算法基于全局提取特征的特点，分别在高像素和低像素模型上进行3种预处理的组合处理，然后从类间差值和类内差值两个方面考虑预处理方法对算法的影响。

3.1.1 Eigenface 的类间差值模型

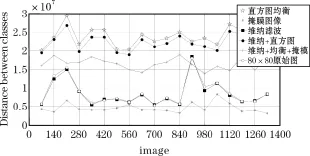
图2 80×80尺寸的类间欧式距离比较仿真图

图3 40×40尺寸的类间欧式距离比较仿真图

图2所取得的曲线是根据人脸库中第一个人的首幅图像与剩余所有人的1393张图像的类间欧式距离的走势图。对比图2的高像素模型和图3的低像素模型，相同之处在于直方图均衡后所得到的类间距离是最大的，形成对比的是掩模技术将背景的差值归于零，经过图像掩模技术处理后的图像的类间距离是最小的。为了减小噪声对于类间差值的干扰，实验引入维纳滤波，无论像素大小在原始图像上进行维纳滤波，消除噪声效果都不理想，而在进行了直方图均衡处理后的图像上进行维纳滤波，类间距离下降明显，图2高像素中类间距离平均下降1×106，下降比例为4%;图3中的低像素模型效果更加显著，类间距离约也下降了1×106，下降比例为16%。经过均衡和滤波后，加入图像掩模获得距离曲线位置适中，且仍高于原始图像曲线的位置，低像素模型的曲线走势更加平缓，高像素模型相对于原始图像类间距离平均提升了6.94×106，约为79%的涨幅，低像素模型相对于原始距离平均提升1.93×106，约为89%的涨幅。

换句话说，经过3种图像预处理后的类间距离整体有显著的提升，同时去除掉一些因噪声和无关信息干扰所造成的类间距离突变，有利于Eigenface进行识别，并且预处理对低像素图像的类间差值处理效果较高像素图像更加明显。

3.1.2 Eigenface 的类内差值模型

从图4不难发现，图像掩模是对类内距离的降低是最有帮助的一种预处理方法，并没有改变原始图像类内距离的基本走势和形态。直方图均衡极大地突出了类内特征，使得类内距离起伏增大，但是造成类内距离增加幅度较大，引入维纳滤波来降低噪声的干扰，虽然在原始图像上没有起到明显的作用，但是引入到经过直方图均衡后的图像中去，类内差值降低的效果较为突出，在此基础上再加入的图像掩模处理使得类内差值进一步得到了降低。

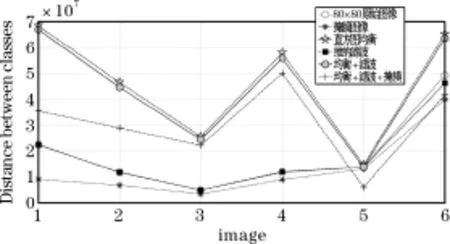
图4 80×80尺寸的类内欧式距离比较仿真图

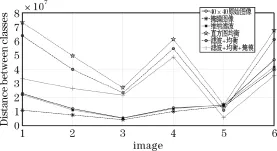
图5 40×40尺寸的类内欧式距离比较仿真图

与此相对比的图5所示的低像素模型，差异之处在于低像素环境中的类内差值的最大值下降明显，高像素模型类内距离下降1.83×107，幅度约为26%，低像素模型下降了6.13×106，降幅为33%。同时在低像素的环境中引入维纳滤波，高像素模型在3种预处理方法下相较于原始图像类内距离增加1.172×107，增幅为61%，而低像素模型增加2.39×106，增幅为50%，低像素模型经过预处理后增幅小于高像素模型，这对于识别更为有利。

为进一步验证上述仿真结论和预处理实际应用效果，在加入不同的预处理方法后形成多个人脸库，在CUP为Intel Core2 Duo T7250(2.0 GHz)的计算机条件下下进行识别率和效率测定，取200人的各2幅图像共400幅图像作为带识别人脸库，同其余1000幅图像进行识别率计算，得到了表1中的识别率和识别时间。

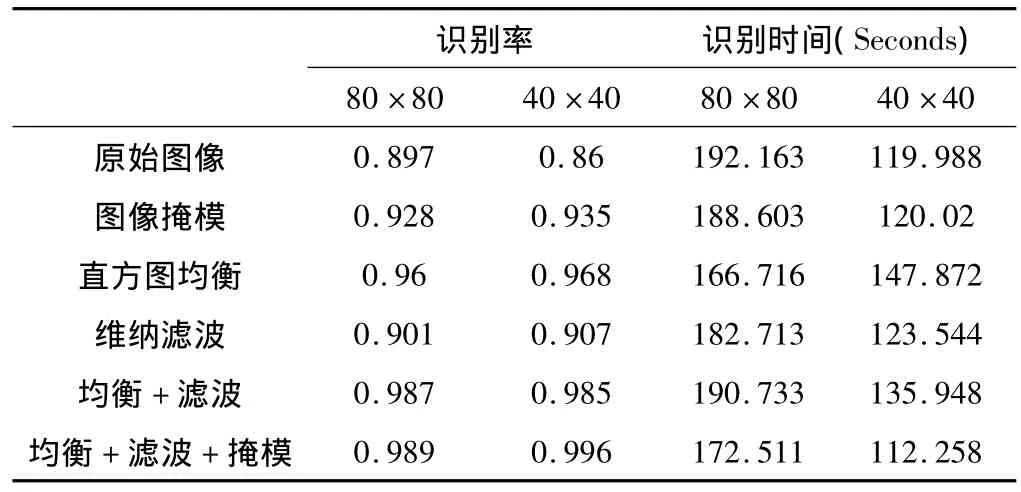
表1 Eigenface在高像素与低像素下不同预处理的识别率和识别时间

综合Eigenface的类间差值模型和类内差值模型的预处理实验，经过了直方图均衡、维纳滤波和图像掩模后的人脸识别率是最高的，并且低像素模型的识别率高于高像素模型，在表中另一项明显的特点就是低像素模型在同等的预处理条件下，要显著小于高像素模型。这就使低像素模型表现出高识别率和高识别效率的特点，这在工程上有一定的优势，两种模型经过预处理后的识别时间都有所下降，帮助算法从另外一个途径上降低了复杂度，提高了运行效率。

3.2 Fisherface的仿真实验

图6和图7分别展示了高像素模型和低像素模型的类的散度刻画比较，图中数据通过计算matlab仿真出的散度矩阵的迹而获得的。

图6 80*80尺寸类的散度刻画比较

图7 40*40尺寸类的散度刻画比较

根据公式(6)，期待获得较大的目标函数Js(a)。高像素模型如图6所示，图像掩模技术虽然降低了类内散度，但是降低的类间散度幅度过大，造成了目标函数的值得下降。直方图均衡技术在大幅度增加类间散度矩阵的同时，也极大地增加了类内散度，所得目标函数是最小的一个，在原始图像上进行的维纳滤波对于3种矩阵的迹的影响都较为微弱，但在进行直方图均衡后引入维纳滤波后，滤波的效果更为明显，修正了单纯直方图均衡后类内散度过大的缺陷，使目标函数Js(a)有小幅度提升。但在此基础上再引入图像掩模技术，使类间散度下降过大，适得其反地造成了目标函数的降低。图7所示的各种预处理方法对于Sb和Sw的变化总体趋势与图6中类似，但是目标函数Js(a)的迹的值的变化却有很大的不同，如表2中所示低像素模型中单一的维纳滤波后的目标函数获得最大值，加入图像掩模后更是使目标函数Js(a)在两种模型下都有所降低。

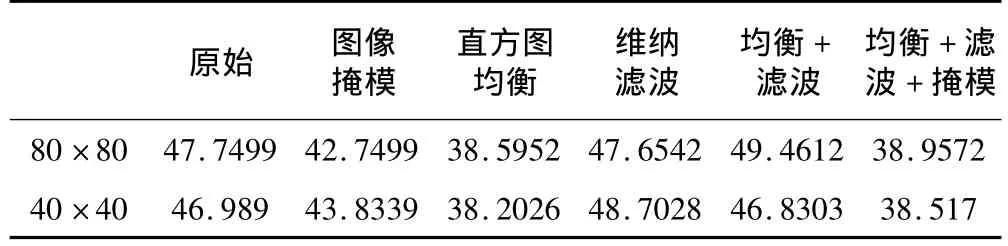
表2 高像素与低像素下不同预处理的目标函数矩阵的迹

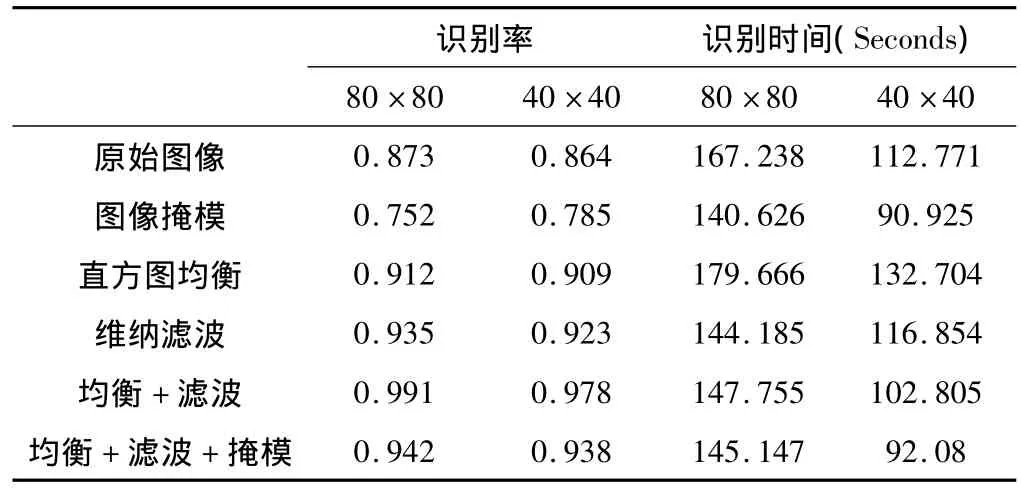
表3 Fisherface在高像素与低像素下不同预处理的识别率和识别时间

在同样硬件条件下用和Eigenface相同的人脸库进行识别率测定，得到Fisherface的识别率和识别时间如表3所示，从各种预处理对于目标函数Js(a)的影响来看，图像掩模并不适合Fisherface，先用直方图均衡进行图像增强后，再引入维纳滤波所获得Js(a)最符合Fisherface准则的要求，高像素下此时Js(a)值最大，而低像素在维纳滤波下Js(a)提高的最多。同时从处理效果来看，高像素模型下类间散度矩阵的迹在直方图均衡和维纳滤波两种预处理下相较于原始图像提高了70%，而低像素模型之提升了62%，高像素模型的类内散度矩阵的迹同低像素模型的变化相同，同时提升了3倍之多，目标函数方面，高像素模型增加了5%，低像素模型减少了0.3%，而低像素模型在维纳滤波处取得了最大的值，也只提升了3.6%。再结合表3中得到的识别率，高像素模型在直方图均衡和维纳滤波条件下得到的识别率高于其他情况，Fisherface在高像素模型的情况下处理效果明显优于低像素模型的情况，但是低像素模型的识别时间却明显少于高像素模型。

4 结束语

经过分析和比较，直方图均衡、图像掩模和维纳滤波3种预处理方式的组合适合处理Eigenface算法的人脸库，获得的类间距离较大的同时得到较小的类内欧式距离，与此同时，低像素模型也更加适合用于Eigenface算法，在获取到的人脸图像像素质量不佳的情况下更适合选择Eigenface算法。而Fisherface算法的预处理应选择直方图均衡和维纳滤波技术的组合，在这两种方法的组合下获得的目标函数最大，得到了较高的识别率，同时Fisherface应选择像素较高的人脸库进行匹配识别，得到的识别效果会更好。Eigenface在3种预处理方法下，识别率提高了15.8%，识别效率增加了10.2%，Fisherface识别率提高了13.5%，识别效率则提高了11.6%。识别率的提高，也从另一个侧面验证了预处理技术对于人脸识别系统抗干扰能力的提升及系统强壮性的增加。

实验展现出了更多问题，例如高低像素对于不同算法的影响的原理性解释，还有在识别过程中发现的识别率和效率不能兼得的问题，仍有待继续深入的探索研究。

致谢:感谢成都信息工程学院基金项目(J201206)对本文的资助

[1] Lades M.Distortion invariant object recognition in the dynamic link architecture[J].IEEE Trans on Computer，1993，42(3):300－310.

[2] Belhumeur P N，Hespanha J P，Kriegman D J.Eigenfaces vs.Fisherfaces:Recognition using class special linear projection[J].IEEE Transactions on Pattern Analysis and Maehine Intelligence，1997，19(7):711－720.

[3] 谢永林.LDA算法及其在人脸识别中的应用[J].计算机工程与应用，2010，46(19):189－192.

[4] 李晓东.基于自空间和流形学习的人脸识别算法研究[M].山东:山东人民出版社.2013:47－64.

[5] 山世光.人脸识别中若干关键问题的研究[D].北京:计算机研究所，2004.

[6] 徐琳俊.数字图像分割算法研究[D].镇江:江苏科技大学，2011.22－36.

[7] 李慧元，姜心蕊，徐国贤，等.基于直方图的图像增强技术在图像处理中的应用[J].科技信息，2014，(11):83－84.

[8] 张然，汤全武，史崇升.基于递推最小二乘自适应滤波算法的图像去噪[J].计算机应用与软件，2014，(4):194－196.

[9] 苑娟，万焱，褚意新.熵理论及其应用[J].中国西部科技，2011，(5):42－44.

[10] 王志胜，甄子洋.非线性信息融合估计理论[J].宇航时报，2009，30(1):8－12.

[11] Wang X G，Tang X O.A unified framework for face recognition[J].IEEE Trans.PAMI，2004，26(9):1222－1228.

[12] 孙越泓，魏建香，夏德深.基于互信息与类距离测度最优的图像聚类[J].计算机工程与应用，2011，(34):199－202.

[13] 郭微，孙玉祥.矩阵非奇异性的判定[J].北华大学学报(自然科学版)，2006，(3):93－96.

[14] 孙即祥.模式识别中的特征提取与计算机视觉不变量[M].北京:国防工业出版社，2001.