基于谱图理论构建快递应急配送网络
2015-01-04李双东王丽霞祝静静
李双东*,王丽霞,祝静静
(安徽大学 江淮学院,合肥 230031)
电子商务的兴起推动了快递行业的迅猛发展。快递业是依托配送网络发展的产业,配送网络是企业最重要的资产,是实现快递服务的物质基础和重要保障,对快递服务质量和水平有着决定性的影响。快递配送本身的属性使突发情况不可避免,因此应急网络的运行将保障货物的准时到达。欧忠文等[1]提出应急物流概念,指出可以通过应急处理机构的建立、技术平台的构建和应急手段的启用来实现应急物流;余朵苟等[2]针对我国应急物流系统存在的问题,从指挥决策、运作框架、保障机制等3个层面构建了适合我国应急物流的决策运作体系;谢明[3]对高效应急物流运行机制进行了探讨;苏彩[4]对应急物流管理能力提升进行了探析。
谱图理论主要研究图的结构与图谱之间的关系及性质。本文引入配送网络图模型,应用谱图理论现有结果对现行快递配送网络进行结构分析,给出一种应急网络——环形放射状快递配送网络。
1 配送网络图模型
快递配送网络是依附于交通运输网络上的一种特殊网络,由众多的快件取送点、各级中转场站(集散中心)和运输路线,按一定的原则和方式连接起来的传递系统。它是由区域中转中心之间、区域内多级中转点之间以及中转点和取送网点之间的连接路线构成,相对应的配送网络划分为区间干线网、区内干线网和市内网3个层级。
网络图模型G=(V,E),其中:V为顶点集;E为顶点集V的二元子集。考虑到配送网络结构的组成,将快递配送网点和消费者表示为图的顶点集,自然的网点之间以及网点到消费者之间的配送线路即为顶点集的二元子集,记为图的边集,这样就产生了配送网络图模型。
快递配送网络连通度即为其图模型的连通度。于是,图模型的点(边)连通度即为配送网络的点(边)连通度,图模型的Laplace矩阵对应的次小特征值即为快递网络代数连通度。图的相关定义及简单结果见文献[5]。
2 现行快递配送网络
线性快递配送网络通常采用星形结构,如图1所示。其优点是省时省力,便于管理和业务的扩展。但若网络中有一个网点出故障,那么此网点所承担的业务将受到极大影响,甚至业务归零。尤其在处理应急情况时会带来更大的经济损失,这对于快递企业的生存发展是极大的威胁。

图1 星形配送网络结构图
根据配送网络图模型定义,将图1中的星形结构图视为含有7个顶点的星图S7。易知S7的点、边连通度均为1,只要删除图中的任何一个顶点或一条边,此图就不连通了。经过简单的代数计算可知:S7的代数连通度也为1,即S7的连通性较弱。因此,S7所对应的配送网络结构的连通性很弱,在处理应急情况时存在致命的隐患。
3 快递应急网络的构建
为改善星形结构的不稳定性,可以增加中转场(或网点)的个数。但增加中转场(或网点)的个数会增加企业投入,压缩利润空间,且应急网络只是在紧急情况时的备用网络,因此,应急网络应以常规网络结构作为构建基础。笔者结合蛛网模型设计了环形放射状配送网络,如图2所示。该结构在下一级网点间建立配送路线,但仅限于比较近邻的网点间,这样就行成了一个上级网点和众多下级网点间的封闭系统。该结构具备了星形配送网络的优点,在正常运转时能满足现有网络的要求,紧急情况时能规避现有网络的缺点。

图2 环形放射状配送网络图
4 应急网络连通性分析
由上述分析可知,常规星形网络的点连通度为1,环形放射状应急网络的点连通度为3;常规网络的边连通度为1,应急网络的边连通度为3。
当网络增加到一定规模时,寻找网络图的点(边)割集使得网络图不连通是不易做到的,甚至涉及到计算机的算法编程,因此,只需通过一个较为直接简单的方式来判断其连通性的优劣。代数连通度只需计算各自对应矩阵的特征值作比较,因此,将代数连通度作为重点指标进行分析。
星状快递网络图一般以网点或中转站作为图的中心顶点,即从该顶点连出的边数为n-1(n为顶点数)。根据快递网络的实际情况以及示例的繁简程度,只选取n=5的情形加以分析,星图S5结构如图3所示。

图3 n=5的星状快递网络图
S5的邻接矩阵为:
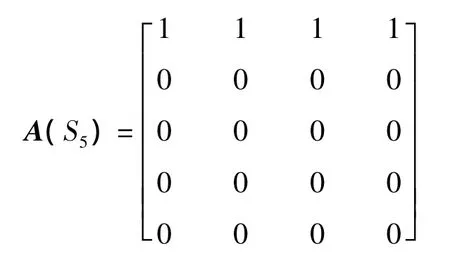
度矩阵为 D=diag{4,1,1,1,1},从而可得Laplace矩阵为:
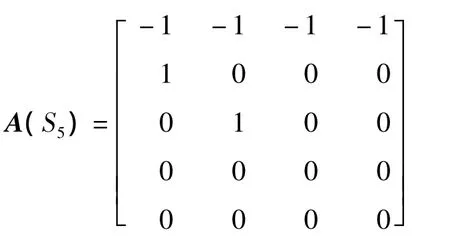
通过计算可得Laplace矩阵的特征值,可知其代数连通度为α(S5)=1。对于应急网络同样给出n=5的情形,结构如图4所示。

图4 n=5的环状快递网络图
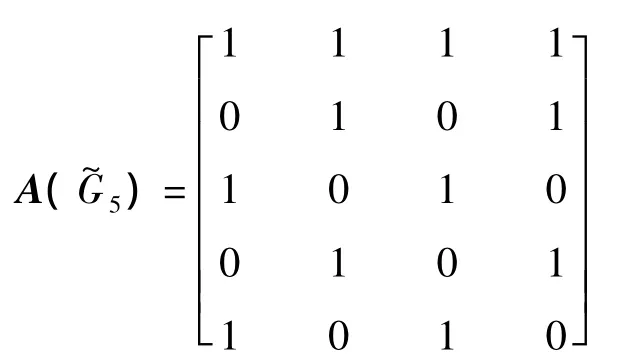
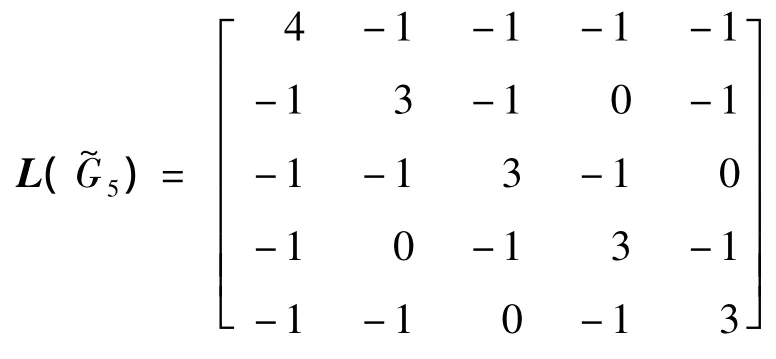
通过计算得到Laplace矩阵的特征值,可知其代数连通度为 α(=3。
二者做一简单对比,可知在连通性上应急网络更加稳定,这也符合了应急网络的构建原则。
5 结语
本文引入快递企业配送网络图模型,在现行常规星形配送网络的基础上,考虑到成本和应急需求,构建了环形应急配送网络。并利用图模型,结合谱图理论相关概念结论,进一步从量上论证了所构建应急网络的合理性。
[1]欧忠文,王会云,姜大立,等.应急物流[J].重庆大学学报,2004,27(3):164-167.
[2]余朵苟,何世伟.应急物流体系构建研究[J].物流科技,2008(11):1-5.
[3]谢明.构筑高效应急物流运行机制的探讨[J].物流科技,2008(11):53-55.
[4]苏彩.提升我国应急物流管理能力探析[J].物流科技,2013(5):33-35.
[5]CHARTRAND G,ZHANG P.图论导引[M].范益政,汪毅,龚世才,等,译.北京:人民邮电出版社,2007.
