同步发电机励磁系统的无模型控制研究

王桂艳，施伟锋，张 威

（上海海事大学，上海 201306）

0 引言

励磁控制对稳定发电机的端电压、调整电力系统的无功功率具有重要的作用，故对发电机励磁控制的研究具有十分重要的意义。发电机组是一个具有强耦合性的非线性系统，通过辨识得到的降阶线性模型准确性差，故基于降阶模型的控制效果很难保证。针对系统的非线性特点，模糊控制[1]、人工神经网络[2]等智能算法被广泛应用于励磁系统的控制。模糊控制依赖专家经验，神经网络模型形式复杂，计算量大，不利于工程实现。因此，寻找不依赖精确模型，在线计算快、综合控制效果好的算法具有很重要的意义。数据驱动控制是一种基于数据的控制方法，在不同领域得到了较好的应用，在励磁控制方面也取得了一定的研究成果。文献[3]将迭代学习控制引入励磁控制系统，结合PID反馈控制和迭代学习前馈控制设计了励磁控制器，使系统在有限时间内迅速准确地跟踪期望轨迹，且具有更好的鲁棒性。文献[4]设计了发电机的基于无模型控制算法的广域阻尼控制器，该控制器在系统发生故障和扰动期间可实现参数的自动调整，解决传统广域阻尼控制器在部分运行方式下性能降低的问题。

无模型自适应控制(Model Free Adaptive Control，MFAC)是数据驱动控制算法的一种形式，由候忠生于1994年提出[5]。它不依赖对象的数学模型，根据输入、输出数据实现系统的控制，在交通运输、化工、直线电机控制、锅炉温度控制、轮船减摇、电力行业等得到广泛的应用[6]。该方法具有算法简单、适用于非线性系统的特点。

本文在分析无模型自适应控制算法的基础上，针对具有稳态增益的系统，提出了改进的无模型控制算法。以机端电压为控制目标，设计了基于无模型控制算法的励磁控制器。发电机的单机系统仿真结果表明了无模型算法应用于励磁控制的有效性。

1 励磁系统模型

励磁控制系统由 AVR(自动电压调节器)、励磁机和同步发电机组成。本文研究的发电机交流励磁控制系统，如图1所示。

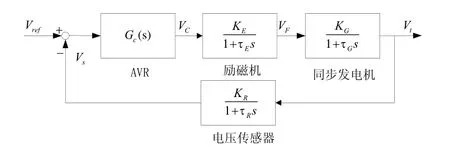
图1 发电机交流励磁控制系统

Gc(s)表示自动电压调节器的传递函数。

励磁机模型可表示为：

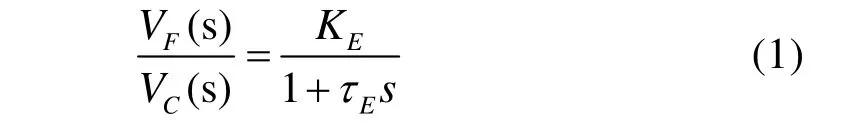
其中，KE为励磁机增益，一般取为1，Eτ为励磁机负载时的时间常数。

发电机的线性化模型可以表示为：

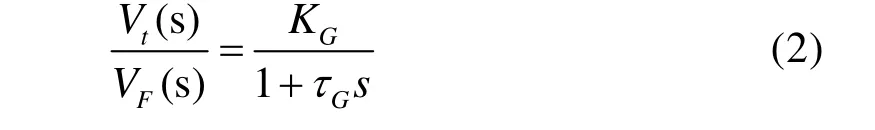
其中，KG表示发电机计及饱和后的动态增益，是发电机偏差ΔVG和励磁电压偏差ΔVF的比值，Gτ为发电机的时间常数；发电机从满载到空载的取值为KG＝0.7～1，Gτ＝1～2s[7]。

电压传感器模型可表示为：

其中，KR为传感器增益，Rτ为时间常数，其值一般为：0.001～0.06s。

2 无模型自适应控制的基本原理

2.1 无模型自适应控制原理

考虑单输入单输出(SISO)非线性系统：

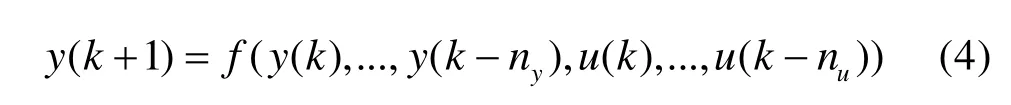
其中，y(k)∈ℝ，u(k)∈ℝ分别表示在k时刻系统的输出和输入数据；ny,nu为正整数，表示未知系统的阶数；f(·)为未知的非线性系统。

假设被控系统满足以下条件：1)对某一给定的系统期望输出yd(k)，存在一致有界的可行控制输入信号，使得系统在此控制输入信号的驱动下，其输出等于期望输出yd(k)；2)f(·)关于各个变量都存在连续的偏导数；3)系统满足广义 Lipchitz条件，即满足对任意的k和 Δu(k)≠ 0，不等式成立。其中，b为一常数

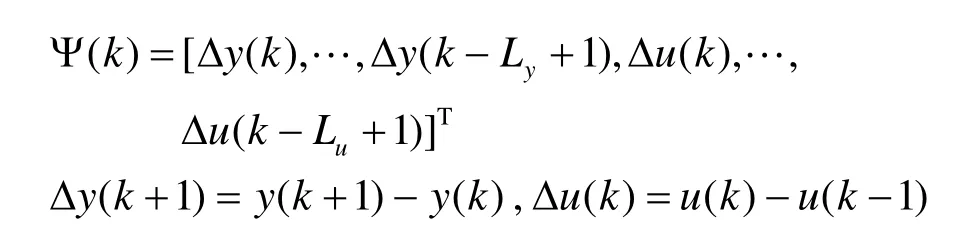
若系统(4)满足以上假设条件，对整数Ly（0≤Ly≤ny）和Lu(1≤Lu≤nu)，则一定存在一个伪梯度向量Φ(k)，使得被控系统可描述为如下的动态线性化形式：

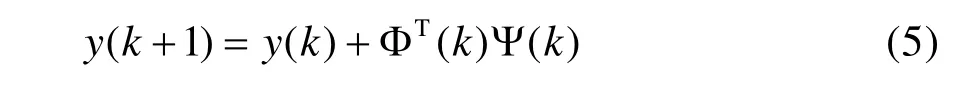
考虑梯度准则函数：

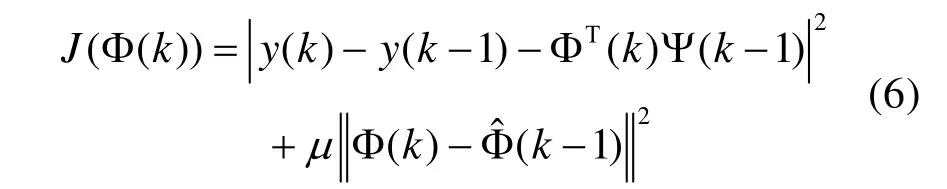
极小化准则函数(6)，可得伪偏导数的估计值：

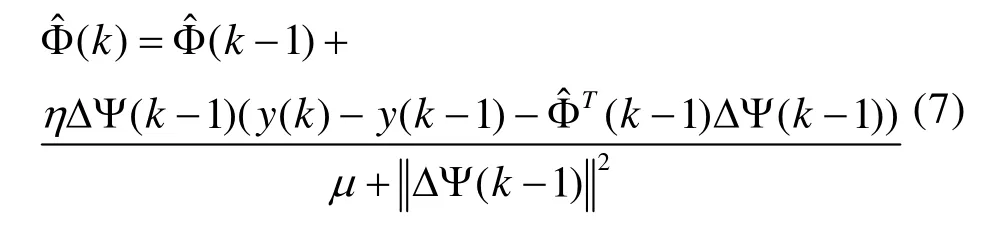
其中，μ＞0，为权重因子，η为步长因子，η∈(0,2]，Δ Ψ(k)＝Ψ(k)-Ψ(k-1)。若≤ε，则(k)＝(1)。其中ε是一个充分小的正数，Φˆ(1)为伪梯度向量的初始值。

考虑控制准则函数：

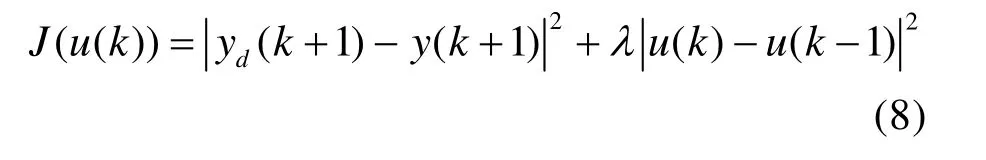
式中，λ＞0，为权重因子，影响系统的快速性和稳定性；yd(k+1)为期望输出。

极小化式(8)，可得MFAC的控制率，如(9)式。其中，ρ为步长因子，ρ∈(0,1]。

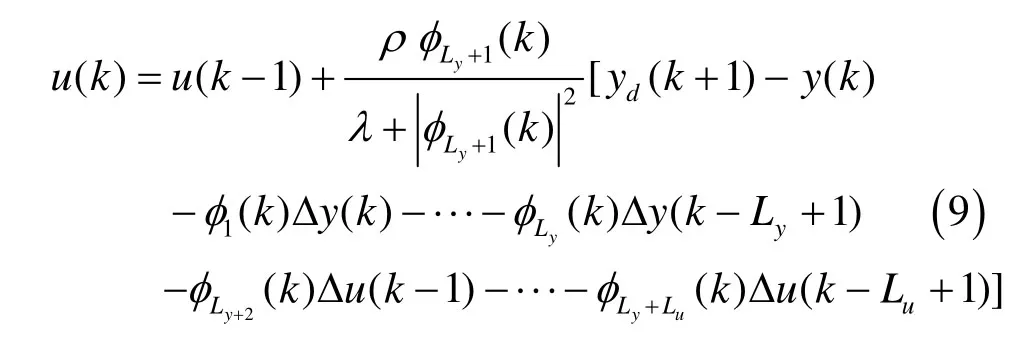
2.2 改进的无模型控制算法

无模型控制器的设计从功能组合的角度出发，即根据系统的控制功能要求，得出满足控制要求表达式，最优化组合功能得到相应的控制率。

实验研究发现，无模型控制方法应用于励磁系统控制的快速性并不理想。考虑具有稳定增益的系统，当系统稳定时，控制器的输出控制量和被控对象的输出是一种固定增益的线性关系，基于这一点，本文进行了一种改进的无模型控制方法研究。

考虑系统(4)，假设此系统具有稳态增益，并设其静态模型如式(10)所示。

其中：为系统的稳态增益，c为常数。

控制准则函数：

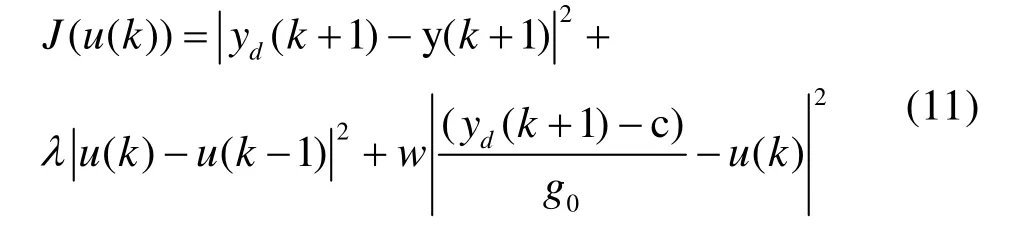
其中，w＞0为权重因子，w与λ一同限制控制量u(k)的变化，从而影响系统的响应速度。

取Lu＝1，Ly＝0，对准则函数(11)求极小值，得改进MFAC的控制率：

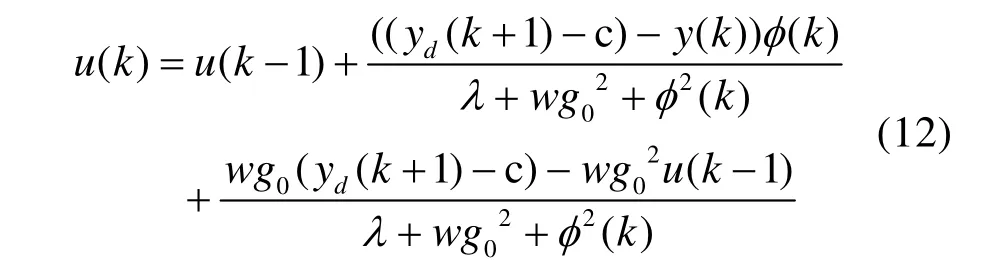
对比准则函数(8)和(11)，准则函数(11)中增加了一项。当系统稳定时，u(k)与yd(k)是一种线性关系，故从理论上来讲，准则函数中新增加的一项有利于提高系统的快速性。令式(12)中的w＝0，即可得普通的无模型控制率。

将无模型控制算法应用于同步发电机励磁控制，控制原理如图2所示。首先，MFAC动态线性化模块由励磁系统的输入、输出数据的增量构建性能指标，最优化性能指标得到伪偏导数的估计值；然后MFAC控制输出模块结合伪偏导数，最优化控制性能指标计算输出控制量u(k)，从而实现励磁系统的无模型控制。通过不断地辨识伪偏导数，调整输出控制量，实现整个励磁系统的实时控制。

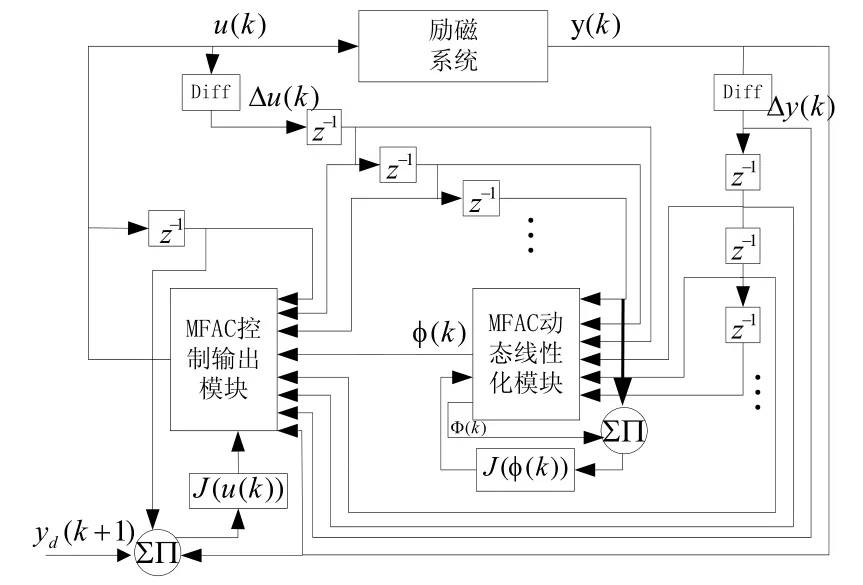
图2 发电机励磁系统的无模型控制原理图

3 单机系统仿真研究

根据图2所示的励磁系统的无模型控制原理图，进行仿真，对比分析发电机空载及带载情况下无模型自适应控制方法的性能。

3.1 发电机空载仿真分析

设置励磁系统参数为：KE＝1，τE＝0.15，KG=1，τG=2，KR=1，τR＝0.02。编写MFAC算法的 S-function，在 Simulink中搭建整个系统的模型。对比分析图1所示的同步发电机励磁系统的MFAC直接控制及改进的MFAC的控制性能。

1)无模型自适应控制

参数设置：λ＝40，ρ＝0.4，μ＝0.16，η＝1，φ(1)＝1.2，Lu＝1，Ly＝0 。

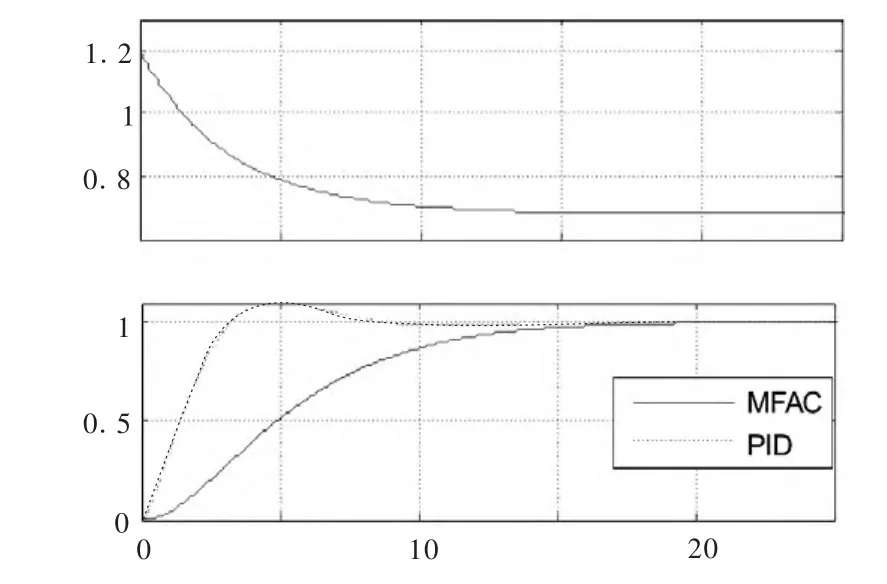
图3 励磁系统MFAC和PID控制仿真结果

仿真结果如图3所示。从图3中可以看出：当t=20 s时，MFAC控制的端电压值达到给定值，即响应时间为20 s，而PID的响应时间为10 s，显然，MFAC算法的快速性不太好。在图中可以看到伪偏导数φ(k)的更新过程，其更新周期与输出响应时间基本一致，这反映了MFAC算法的工作原理，在每个采样周期内，对系统进行辨识得到相应的伪偏导数，然后根据得到的伪偏导数计算控制量，实现系统的控制；当辨识过程稳定时，系统的响应也趋于稳定。

2)改进的无模型自适应控制

参数设置：发电机空载时，根据测定的参数值，得g0＝1，c＝0，λ＝1.1，w＝0.47，ρ＝0.4，μ＝0.16，η＝1，φ(1)＝1.2。

仿真结果如图4所示。从图4中可以看出，改进的MFAC控制的励磁系统的响应时间为4s，相对于普通MFAC，改进的MFAC算法的快速性提高很多；伪偏导数的更新周期约为 3s，符合MFAC的工作原理。而且，w的引入使得算法对其他参数变得不太敏感，参数w的值调整简单，故改进MFAC算法具有很强的实用性。

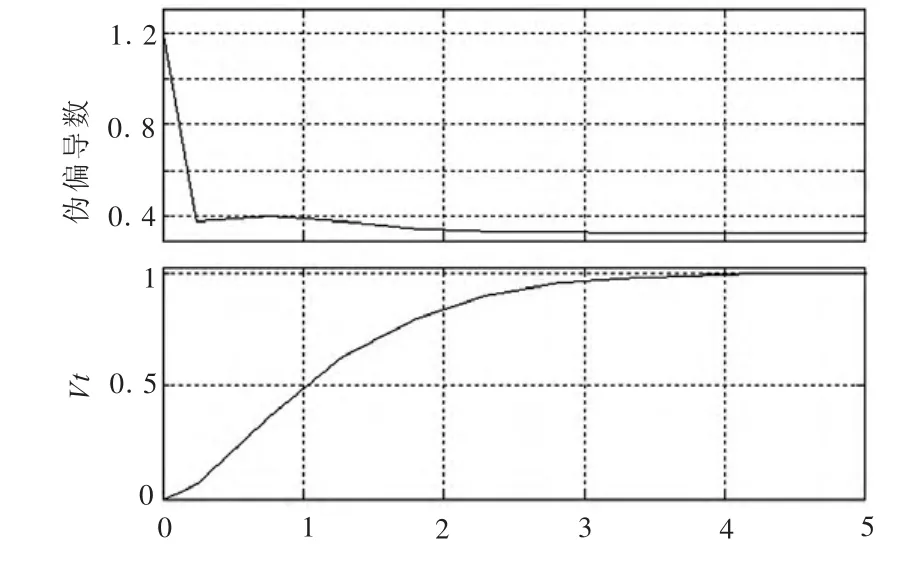
图4 励磁系统的改进的MFAC控制仿真结果

3.2 发电机带载仿真分析

柴油发电机带载仿真如图5所示。柴油发电机的原动机部分采用Simulink中的原动机模型，励磁系统结构如图6所示。

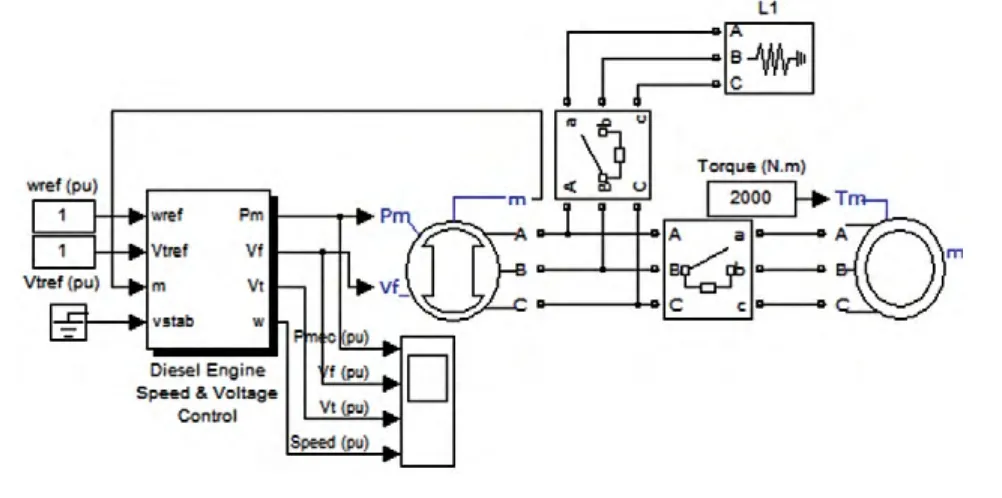
图5 柴油发电机带载仿真图

发电机参数：Pn＝3.125MVA，fn＝6 0Hz，Vn＝2 400V，xd＝1.56，0.296，=0.177，xq＝1.06，=0.177，x1=0.052，＝3.7，＝0.05。

异步电动机参数：Vn＝2400V，Pn＝2250×746W，Tl＝2 000N·mfn＝60Hz，Rs＝0.092，Lls＝0.266/377H，Rr＝0.022Ω，Llr＝0.226/377，Lm＝13.04/377。

负荷1的参数：L1＝1MW。

图6 励磁系统内部结构

柴油发电机带负载 L1和一台电动机运行，由上述的参数设置，发电机的工况已确定。通过实验测得，此稳态工况下Vt/Vf＝1 /1.392。

1)同步发电机励磁系统的改进 MFAC算法仿真分析。

参数设置：g0＝1 /1.392，c＝0，λ＝2.27，ρ＝0.595，μ＝1，η＝1，φ(1)＝1.51，w＝0.1。

图7 改进 MFAC励磁控制的励磁电压和发电机端电压

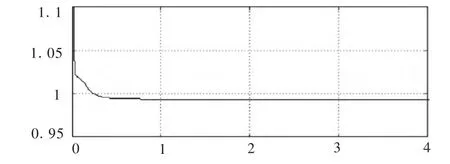
图8 伪偏导数

仿真结果如图7、图8所示。从图7中可以看出：在t=2.7s时，发电机的端电压达到稳态值，改进的MFAC算法进行励磁控制的快速性是很好的，说明了该算法的可行性。从图8中可以看到伪偏导数的更新过程。

2)t=8 s～10 s时，系统的电压传感器受白噪声干扰，噪声功率为0.0001，采样时间为 0.1 s，控制器参数设置不变，仿真结果如图9所示。

在图9(a)中，实线为PID控制的仿真结果，虚线为改进的MFAC控制的结果。可以看出，电压传感器受白噪声干扰后，PID控制的输出电压的波动程度约为 2.5%，改进的 MFAC控制的输出电压约为 0.5%。显然，改进的 MFAC算法比PID算法抗干扰性能更好。图9(b)显示伪偏导数φ(k)的更新情况，在t=8～10 s时，伪偏导数再次更新，t=10 s时，φ(k)的值达到稳定状态。

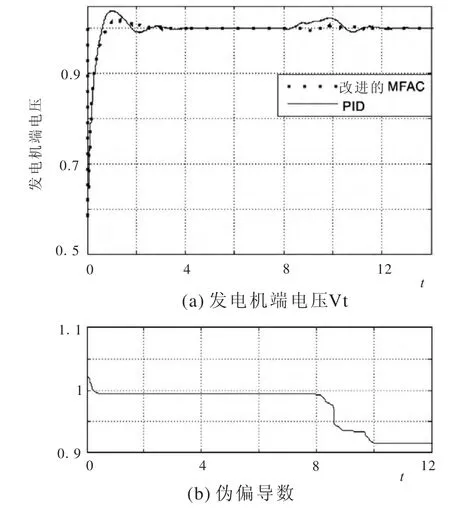
图9 电压传感器受白噪声干扰仿真结果

3)系统的电压传感器发生数据传输延迟故障，延迟时间为0.1 s。仿真结果如图10所示。

从图10(a)中可以看出：当电压传感器发生数据传输延迟故障时，改进的MFAC控制器依然能够实现很好的控制，而PID控制的输出电压产生较大的振荡。图10(b)反映了伪偏导数φ(k)的更新过程。综合2)、3)仿真结果，当传感器出现故障时，无模型算法依然可以实现很好的控制，说明了无模型控制具有很强的自适应性和鲁棒性。

4 总结

本文针对具有稳定增益的系统，提出了一种改进的MFAC算法，算法参数调整简单。对于某一确定工况运行的柴油发电机，运用MFAC算法完成了励磁控制器的设计。从单机系统的仿真结果得出，改进MFAC算法的快速性是比较好的；在传感器发生故障时，MFAC算法展现了极强的自适应性，使得系统在故障情况下仍能够保持很好的稳定性。这也体现了MFAC算法实时更新代表模型信息的伪偏导数的优越性。但本文只是针对于确定工况运行的励磁系统，应用性不是很广泛，MFAC在励磁系统控制中的应用仍需进一步的研究。

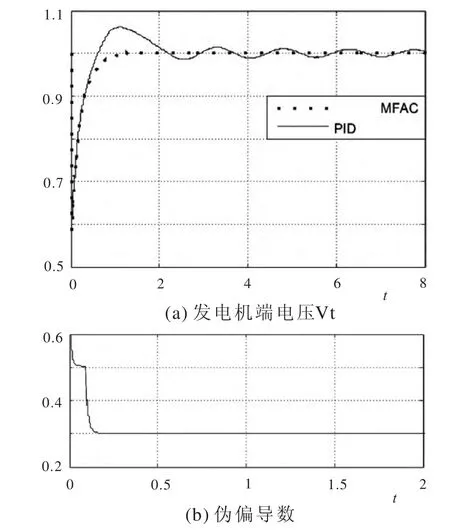
图10 电压传感器数据传输延迟故障仿真结果

[1]贺徽.基于混合智能优化方法的同步发电机励磁控制策略研究[D].武汉:华中科技大学,2011.

[2]施伟锋,陈子顺,汤天浩.船舶发电机励磁系统的CMAC神经网络并行控制[J].电网技术,2005,29(4):31-35.

[3]白敬彩,于少娟,韩如成.同步发电机的反馈-前馈迭代学习励磁控制[J].电机与控制应用,2009,36(3):24-27.

[4]李建,赵艺,陆超,庞晓艳.无模型自适应广域阻尼控制设计方法[J].电网技术,2014,38(2):395-399.

[5]侯忠生.非线性系统参数辨识、自适应控制及无模型学习自适应控制[D].沈阳:东北大学,1994.

[6]侯忠生,许建新.数据驱动控制理论及方法的回顾和展望[J].自动化学报,2009,35(6):650-667.

[7]Zwe-Lee Gaing.A particle swarm optimization approach for optimum design of PID controller in AVR system[J].IEEE Transactions on Energy Conversion,2004,19(2): 384-39.