基于改进型粒子群算法的舰船消磁电流调整方法研究
2015-01-04夏建超徐正喜
夏建超,徐正喜,左 超,耿 攀
(武汉第二船舶设计研究所,武汉 430205)
0 引言
现代舰船大都由钢铁材料建造,在地球磁场作用下会产生感应磁场,造成空间磁场畸变,成为暴露并破坏舰船隐身性能的重要物理特征。加装消磁系统是提升舰船磁隐身性能的重要手段,而消磁绕组电流的调整是影响消磁系统补偿性能的关键[1]。
求解舰船消磁绕组的电流等效于解一个多元一次矛盾方程组,由于该方程组没有确定的解析解,因此通常采用最优解算法比如最小二乘误差(LMS)算法对其进行拟合,然而这种方法主要是减小舰船结果磁场特征的均方根(RMS)误差,它不以求解磁场峰值最小(PM)为目的。
而根据现代舰船磁隐身技术的要求,降低舰船空间结果磁场峰值成为最主要的目标[2]。针对这一目标,本文提出了目标函数为磁场峰值最小的粒子群算法,迭代求解每一个粒子的适应值,最终得到消磁绕组通电电流的最优解。同时为了使该粒子群算法快速收敛,又不至于陷入局部最优,本文通过最小二乘法初步约束粒子位置和速度的范围,对其进行了改进。算例的实施和对比表明,这种改进型粒子群算法具备收敛速度快、优化结果稳定等优点。
1 舰船消磁原理
对采用分区消磁技术的舰船消磁系统,每个消磁绕组电流可单独进行控制,以纵向消磁绕组为例,典型的船舶消磁系统如图1。
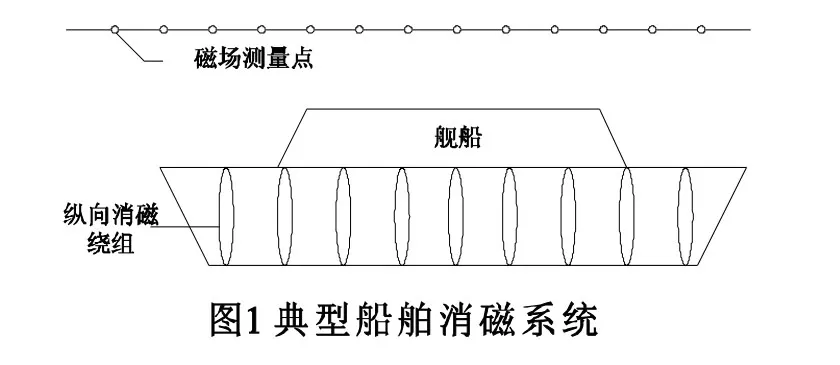
首先,测量舰船在地磁场激励下、典型测量线上的磁感应强度。然后,在无外界磁场激励条件下,分别对每一个绕组通以单位安培电流,在相同的测量线上测量磁感应强度数值,作为该绕组的效率。最后,通过调整各绕组电流,使绕组的叠加磁场与舰船感应磁场尽可能大小相等、方向相反,以达到消磁目的。假设测量线上有m个点,纵向绕组共有n组,第i个区段的安匝量为xi,当安匝量为1时在第j个测量点上产生的磁场为aj,i,而这第j个测量点上的舰船感应磁场为bj;当j从1取到m时,得如下方程组
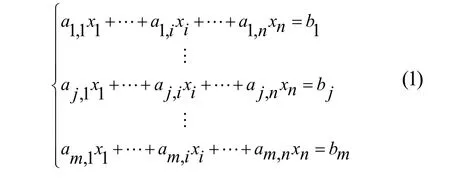
其中bj,aj,i可通过测量得到,方程组左边系数构成绕组效率矩阵A,右边为舰船感应磁场矩阵B,需要确定绕组安匝量矩阵 X,使 AX-B的峰值最小(PM),即可达到较好的消磁效果[3]。
2 算法介绍
2.1 最小二乘法原理
最小二乘法可使上述方程AX-B误差平方和最小,也就是使方程组中每个方程左右两端之差
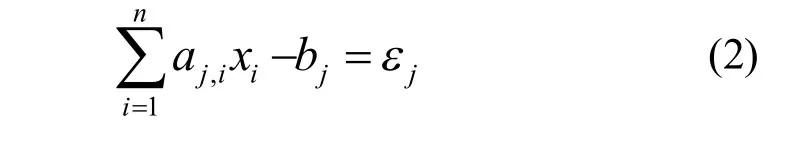
的平方和取极小值,即
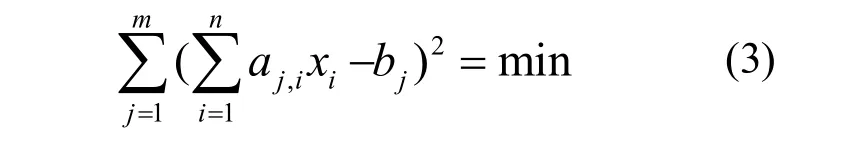
对其求偏导,有
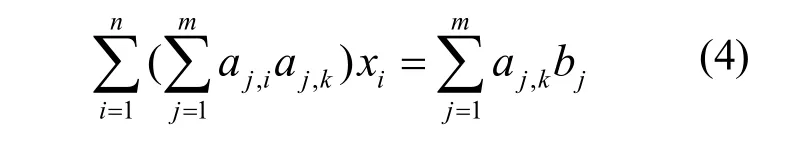
其中k=1,2,…n,若令,,则该方程可用下列矩阵表示

其中,C=ATA,D=ATB,该方程组的解是确定和易求的[4]。
2.2 粒子群算法原理
粒子群优化算法采用群体与进化的概念,将个体看作是在n维搜索空间中的一个没有重量和体积的粒子。首先,在解空间内随机初始化粒子,这些“粒子”在解空间内以某种规律移动,经过若干次的迭代后找到最优解。每一次迭代中,粒子通过跟踪两个值来更新自己:一个是粒子本身的最优解(pbest),另一个值是整个粒子群体当前找到的全局最优解(gbest)。找到这两个值后,每个粒子根据自己的飞行速度,决定自身的走向及飞行距离而不断进化。上述过程可由进化方程描述为:
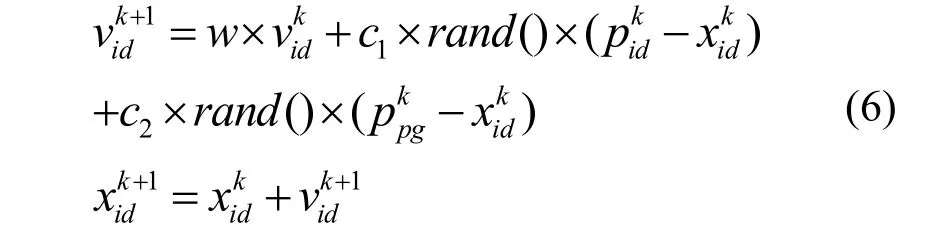
其中w表示惯性权重,i表示第i个粒子,d表示粒子的第d维,k表示第k代,rand()产生[0,1]的随机数,c1、c2表示加速常数[5]。
粒子的位置范围对算法的收敛能力起着重要的作用,合适的粒子位置范围有利于解的快速收敛。粒子的飞行速度有一个最大值vmax,用来限制粒子飞行速度。vmax决定了粒子在解空间的搜索精度,如果vmax太大,粒子会飞过最优解;如果太小,粒子则陷入局部最优解而无法进行全局搜索。因此,通过调整粒子位置、粒子飞行速度可以达到粒子群算法的最佳寻优能力[6]。
2.3 改进型粒子群算法
对进化算法的研究表明,如果能压缩搜索空间,就可以提高优化算法得到最优解的几率[6]。而在以结果磁场峰值最小为目的使用粒子群算法求解消磁电流之前,难以确定每个绕组的电流范围,也难以确定粒子的飞行速度。而以结果磁场方差和最小为目的的最小二乘法却能快速准确的得到每个绕组的电流值。由于两者解的相似性,可将最小二乘法得出的绕组电流范围应用于粒子群算法的程序中,此时粒子飞行速度也会有一个参考,最优解也必须至少小于最小二乘法求出的最小峰值才有价值。
3 算法在舰船消磁电流调整中的应用
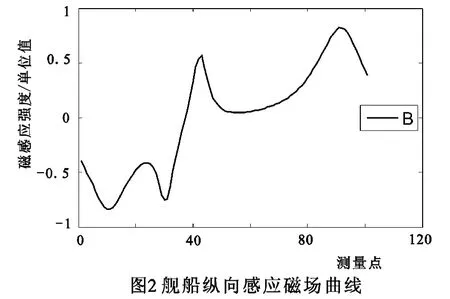
如图1所示的某舰船在只有纵向地磁场激励下,在某测量线101个点上的磁感应强度曲线构成感应磁场矩阵B,如图2。
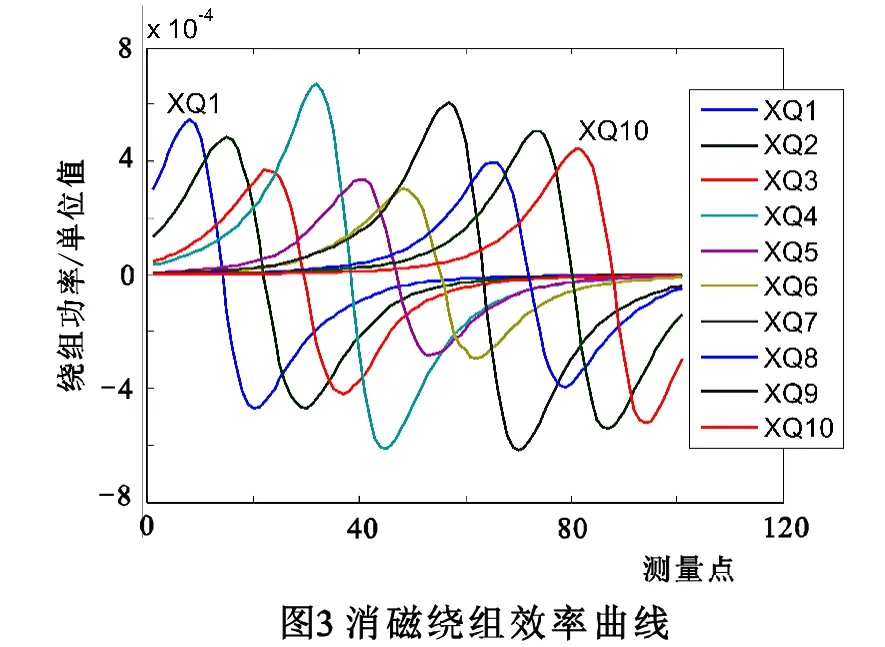
在该船上设置10个纵向消磁绕组,分别单独通电1安培的效率曲线如图3,测量线上的各绕组通电产生的磁场构成绕组效率矩阵A。
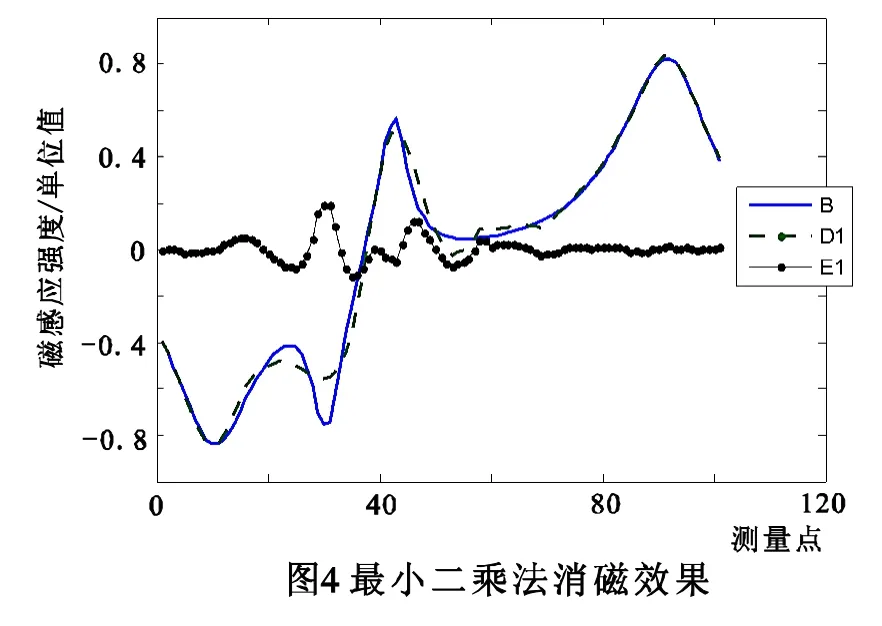
如2.1节所述,由最小二乘法可求解绕组电流矩阵IRMS,在 matlab中,可使用命令IRMS=pinv(A)*B快速得到,将补偿磁场D1=A*IRMS的曲线与感应磁场 B的曲线进行比较,感应磁场与补偿磁场差值即消磁之后的结果磁场为E1=D1-B,如图4所示。
以上最小二乘法求解得到绕组电流值矩阵:

以此作为粒子群算法中粒子位置和速度的变化约束条件,在matlab中,第n个绕组电流范围可设为:
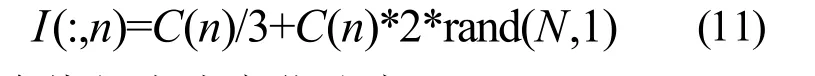
第n个绕组电流变化速度即:
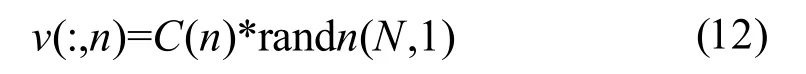
其中N表示粒子数目,C(n)就是IRMS中第n个元素[7]。根据迭代经验,粒子数取N=400,粒子维数(未知数个数)取D=10,学习因子取c1=c2=1.4962,惯性权重w=0.7298[8],最大迭代次数取MaxDT=1 000,目标函数为
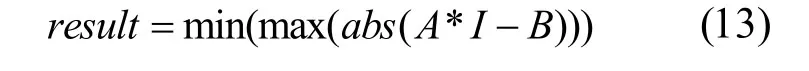
可求出绕组电流矩阵:

将补偿磁场D2=A*IPM的曲线与感应磁场B的曲线比较,并作差值求结果磁场E2=D2-B,如图5。
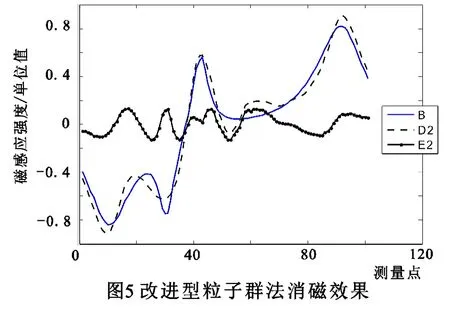
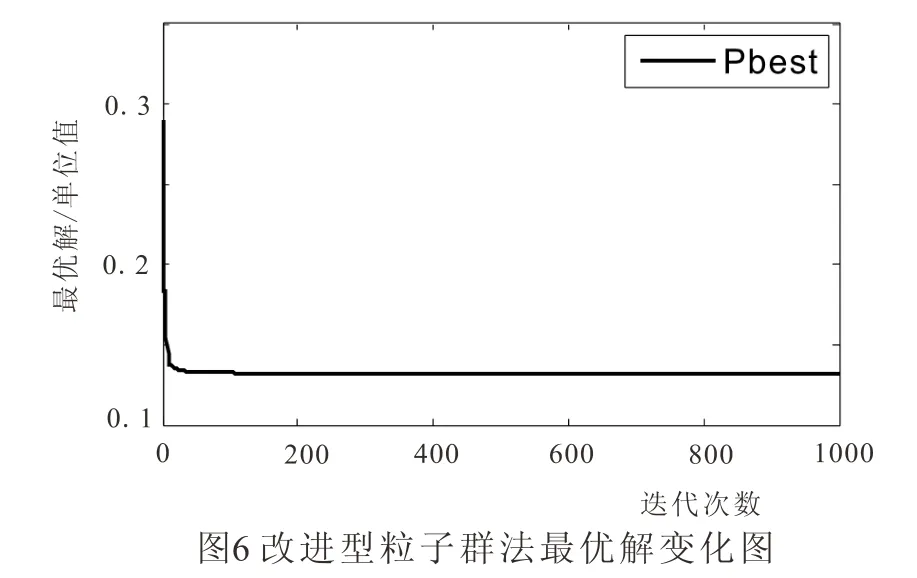
此时结果磁场最大峰值为0.130单位磁感应强度值,相比最小二乘的最大峰值0.194降低33%,优化效果明显。此外,由图6所示的最优解变化图,可知算法在100步左右迭代就已收敛,运算时间只需12 s左右。
如果不采用最小二乘法进行初步约束,而将粒子位置和速度范围设定为随机值,其他条件与上述一致,最优解变化如图7,可见经过5000步计算,结果仍不收敛,且最优解值较大,为0.345,相比最小二乘法的最大峰值0.194升高78%,且在同一台电脑上运算需要1分钟左右。
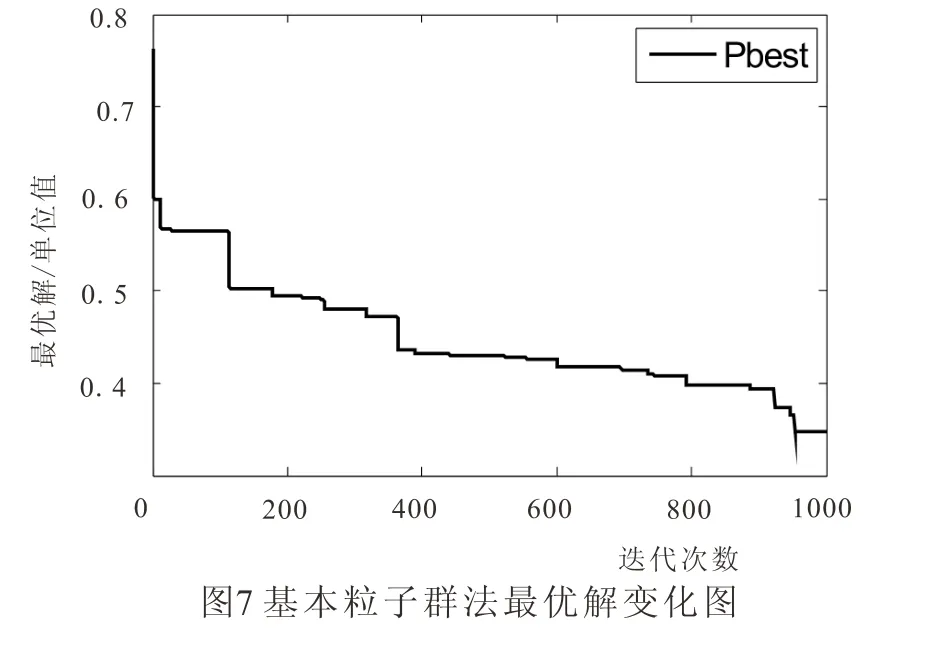
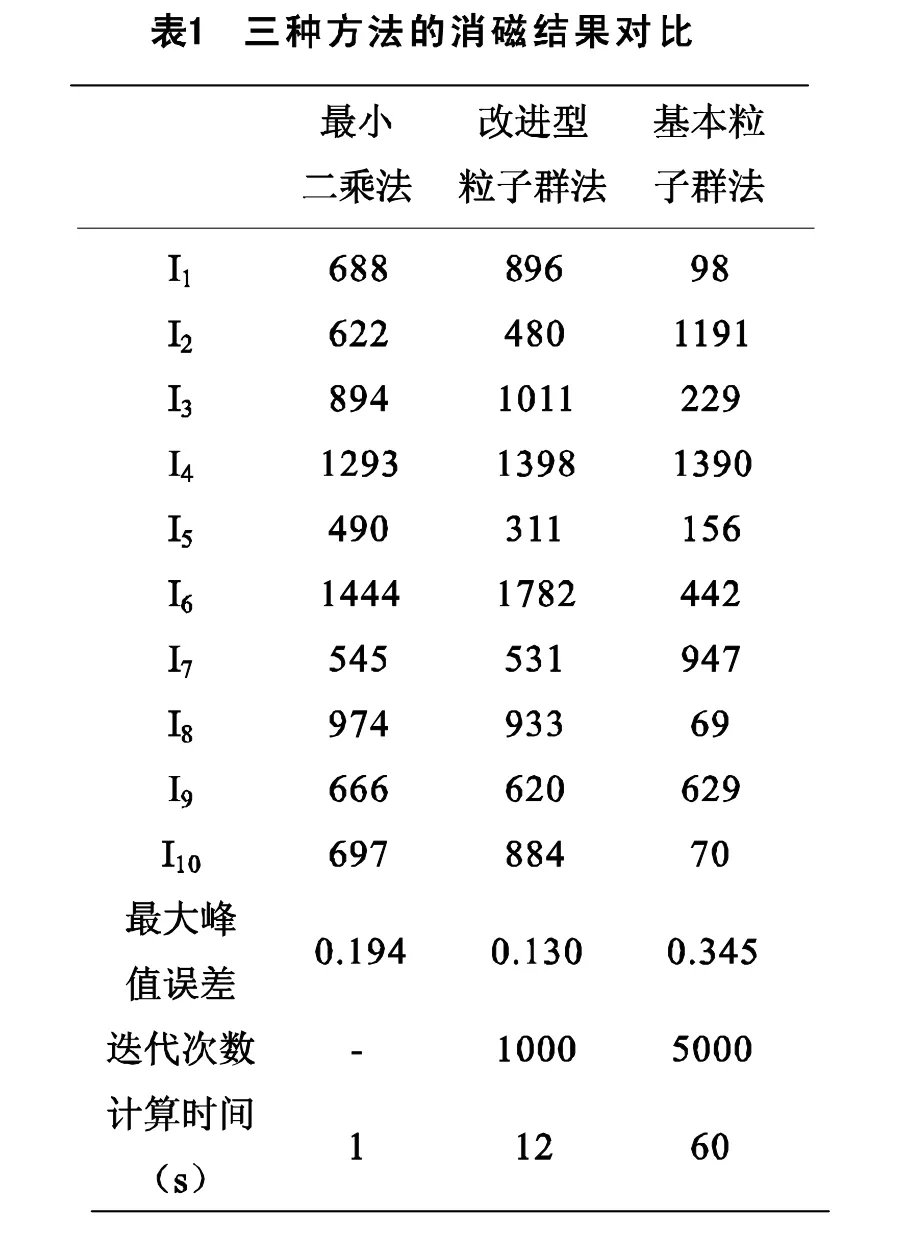
表1对比了三种求解方法的消磁电流、结果磁场最大峰值、迭代次数和计算时间,说明改进型粒子群法在最优解和收敛速度方面具备综合优势。
?
此外,由于基本粒子群算法本身参数的随机性,连续求解10次,所得最优解每次都不相同,而运用改进型粒子群算法求解,最优解稳定性较高,如表2。
4 总结
本文提出了一种改进型粒子群算法用以调整舰船消磁电流,该算法使用最小二乘法的结果来约束粒子群算法中粒子位置和速度的变化范围,限定求解空间和粒子速度,可以得到比最小二乘法和基本粒子群法更优的结果磁场,同时该算法直观易懂、收敛速度快、结果稳定性高,实际算例说明此算法可用于舰船消磁电流的调整优化。

?
[1]张国友.舰船消磁原理及装置[M].武汉: 海军工程大学,2009: 68-92.
[2]韦春健,史振宇.德国海军消磁系统发展现状及应用[J].船电技术,2013,33(06): 36-38.
[3]唐申生,周耀忠,庄清华.大型舰船分区消磁理论研究[J].海军工程大学学报,2003,15(1): 80-83.
[4]刘大明.舰船消磁理论与方法[M].北京: 国防工业出版社,2011: 137-138.
[5]J Kennedy,R C Eberhart.Particle swarm optimization.IEEE International Conference on Neural Networks,Perth,Australia,1995.
[6]胡会超.粒子群优化算法研究进展[A].全国冶金自动化信息网2013年会论文集[C],2013: 200-202.
[7]马莉.MATLAB数学实验与建模[M].北京:清华大学出版社,2010.
[8]周俊,陈璟华,刘国祥,许伟龙.粒子群优化算法中惯性权重综述[J].广东电力,2013,26(7): 6-12.
