考虑徐变的钢－混凝土组合箱梁的变形计算

刘亚茹，刘小洁

(中南大学土木工程学院，湖南长沙410075)

当前，钢－混凝土组合箱梁由于其良好的力学性能在高层结构、大跨度结构等结构中得到越来越广泛的应用，但是，由于混凝土的徐变影响，外荷载保持不变时，钢－混凝土组合箱梁的变形会随时间的增长而增大。而且，混凝土的徐变效应会引起钢－混凝土组合箱梁的内力重分布，从而导致混凝土板应力降低，钢箱梁应力增加。

我国《钢结构设计规范》(GB50017—201X)送审稿初稿中采用等效模量法近似考虑徐变效应，但随着荷载作用时间的延长，混凝土徐变效应对钢－混凝土组合箱梁变形的影响并不一样，因此笼统的取混凝土在长期荷载作用下的变形模量为Ecl=0.5Ec并不准确。国内外学者对组合工字梁在长期荷载作用下的变形进行了研究［3－9］，但对组合箱梁的研究尚不多见，周凌宇等［10－12］对组合箱梁进行了试验研究和理论推导。为丰富钢－混凝土组合箱梁的计算公式，本文对组合箱梁的长期变形问题进行研究和分析，考虑混凝土徐变的影响，建立组合箱梁在长期荷载作用下的挠度变形计算公式。目前国内外尚无组合箱梁的荷载试验，但已有组合工字梁的长期相关试验，由于组合箱梁和组合工字梁的抗弯受力性能相近，因此为验证本文公式的可行性，本文首先借助ANSYS软件，对组合工字梁在长期荷载作用下的受力过程进行有限元模拟，比较实测值和模拟值，得出利用本文建立的有限元模型模拟组合梁在长期荷载作用下的变形是可行的，从而进一步建立组合箱梁的三维模型，比较计算值和模拟值，结果表明本文公式可用于组合箱梁在长期荷载作用下的变形计算。

1 长期荷载作用下钢－混凝土组合箱梁变形计算的理论推导

在荷载长期作用阶段，组合箱梁中的钢箱梁通常处于弹性工作阶段，混凝土板的压应力与应变虽不能保持完全线性关系，但是压应力仍在应力－应变曲线的上升阶段，因此可近似认为压应力沿混凝土翼板截面高度线性分布，故假设:

1)钢箱梁和混凝土板在长期荷载作用下仍处于弹性工作阶段;

2)钢箱梁和混凝土板具有相同曲率，即钢箱梁和混凝土板之间没有掀起。

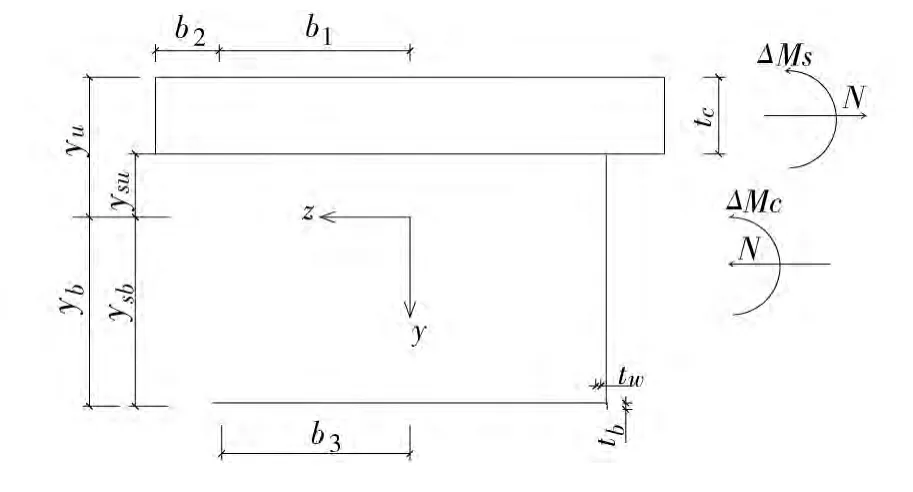
图1 钢－混凝土组合箱梁计算模型Fig.1 Computational model of Steel－ Concrete composite box－beam

由于荷载长期作用期间，截面弯矩不变，故:

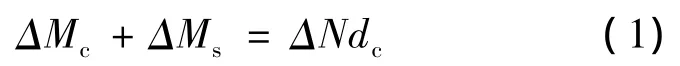
式中:ΔMc和ΔMs分别表示因徐变引起的混凝土板截面和钢箱梁截面的附加弯矩;ΔN表示如图1所示的附加轴力;dc为混凝土板截面形心和钢箱梁截面形心的距离。

混凝土徐变引起的截面附加曲率:

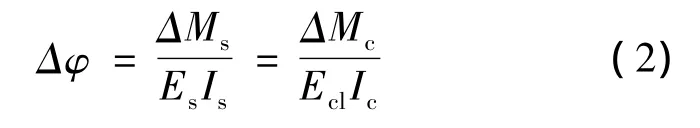
式中:Δφ为混凝土徐变引起的截面附加曲率;Es为钢的弹性模量;Ecl为混凝土考虑徐变后的弹性模量;Is为钢箱梁的截面惯性矩;Ic为混凝土板的截面惯性矩。

钢箱梁底部的附加拉应变和混凝土板顶部的附加压应变分别为

式中:Δεs和Δεc分别为钢梁底部的附加拉应变和混凝土顶板的附加压应变;ysb为钢箱梁底部到截面形心的距离;As和Ac分别为钢箱梁、混凝土板的截面面积;φ为混凝土的徐变系数;εc0为混凝土板顶部的初始应变;hc为混凝土板的高度。

由几何关系可得出附加曲率为

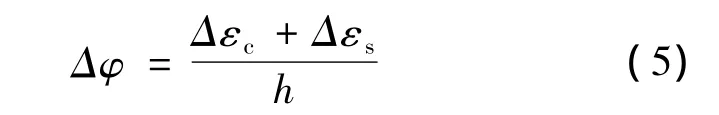
式中:h为组合箱梁的截面高度。

将式(2)和(5)整理可得

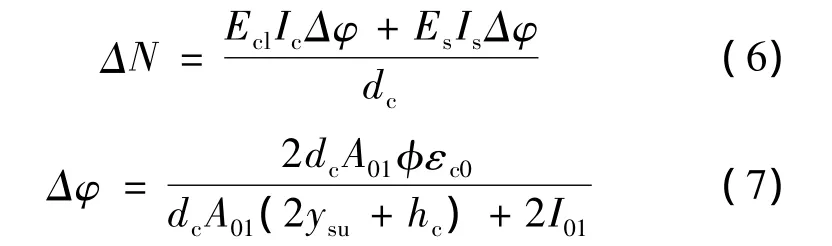
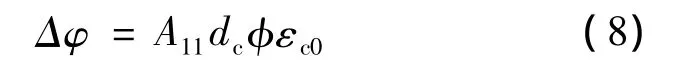
由于长期荷载作用下，钢－混凝土组合箱梁的挠度的增大主要是由混凝土的徐变引起的，因此可认为实际截面曲率为

式(9)中φf为荷载作用开始时产生的曲率。

令组合箱梁沿跨度方的截面抗弯刚度为B(x)，荷载作用下产生的弯矩为M(x)，则式(9)可变换为

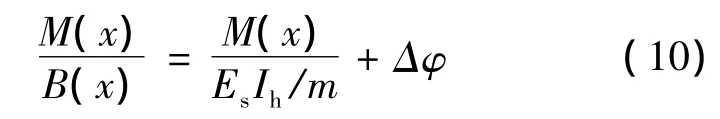
其中m为考虑滑移影响时钢－混凝土组合箱梁的刚度折减系数，按照笔者推导出的刚度计算公式计算:

跨中集中荷载作用下:

均布荷载作用下:

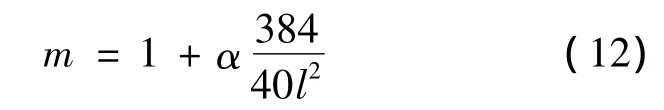
其中:n为钢与混凝土的弹性模量之比;yu为钢箱梁顶部到形心的距离;tb为钢箱底部厚度;p是抗剪连接件的纵向平均间距;Aw为单侧腹板面积;ns为抗剪连接件列数;Ih为换算截面的惯性矩。

将式(8)代入式(10)可以求得在不同荷载作用下组合箱梁的截面抗弯刚度。

跨中集中荷载下:

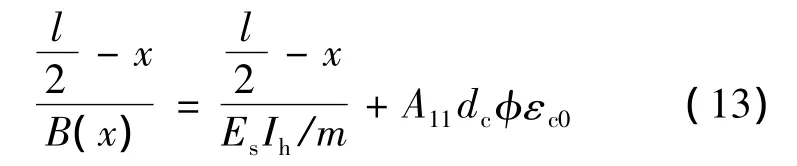
均布荷载下:

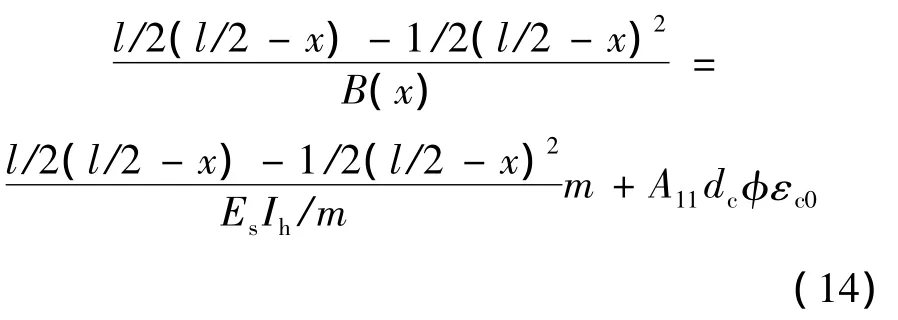
其中，l为箱梁跨度;x为计算截面到跨中截面的距离。

由于文献［13］证明抗弯刚度沿梁长分布较均匀，可近似取等效截面刚度。本文取跨中刚度作为等效截面刚度，因此长期荷载作用下钢－混凝土组合箱梁的抗弯刚度为

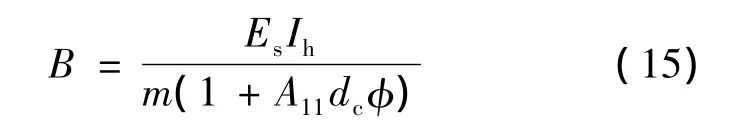
长期荷载作用下，钢－混凝土组合箱梁的跨中挠度计算公式为:

跨中集中荷载作用下:

均布荷载作用下:

2 徐变计算的方法

徐变是混凝土的重要性质之一，大量实验结果表明，应力小于混凝土强度的50%时，徐变应变与应力为线性关系。国内外学者建立了有效模量法、徐变率法、龄期调整有效模量法、老化理论、弹性徐变理论和弹性老化理论等6种徐变计算理论［14］，本文介绍3种常用的计算方法，并通过比较选取本文所用的计算方法。

2.1 有效模量法(EM法)

该方法将徐变问题等效为弹性问题处理，假设荷载不变时，应力与应变成正比，即 Ec=

方法仅在应力无明显变化和混凝土龄期可忽略不计时与试验结果较符合，在应力递增时会高估混凝土的变形，应力递减时会低估变形，而且在卸载时，混凝土的变形将完全恢复，与实际情况不符。

2.2 徐变率法(RC法)

方法假定徐变速率与加载龄期无关，利用该方法仅需要一条徐变曲线，即

该法可以解决许多简单的问题，但是在解答复杂问题时，需要解复杂微分方程，很难得到解析表达式。且应力递增时，低估了混凝土的变形;应力递减时，高估了混凝土的变形，忽略了卸载后的徐变恢复。

2.3 龄期调整有效模量法(TB法)

该方法利用老化系数考虑混凝土老化对最终徐变值的影响，即

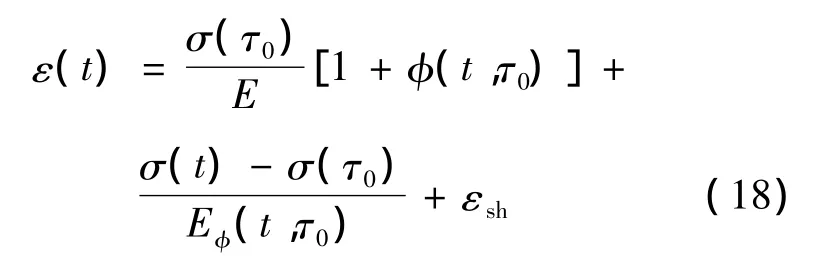
其中老化系数为

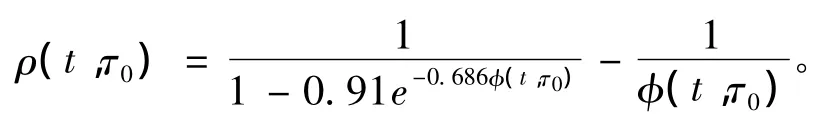
试验［15］证明该方法精确度较高，因此本文采用该方法进行计算。

3 公式验证

首先对文献［6］中的模型GL－1利用ANSYS进行有限元分析。

混凝土单元采用SOLID65单元，钢箱梁单元采用SHELL43单元，栓钉单元采用COMBINE39单元，同时使混凝土板和钢箱梁的水平自由度一致，梁两端采用铰接约束，一端约束x，y和z方向，一端约束y和z方向。为使集中荷载作用处的混凝土板不发生集中破坏，在荷载作用处加垫板，垫板单元采用SOLID45单元，有限的模型见图2。

混凝土徐变准则采用ANSYS提供的creep准则，ANSYS中提供了“显式”和“隐式”2种徐变方法，本文采用显式徐变方法，利用TBOPT=0调用显式徐变方程。显式算法求解徐变使用欧拉朝前法，以时间步开始的应力、应变为基础计算徐变应变率，假定每个时间步长内的徐变应变率为常数:

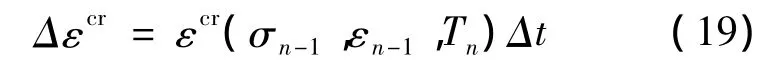
在ANSYS提供的12个徐变方程中，本文使用C6=0的初始徐变方程:

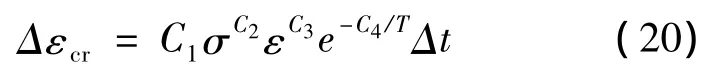
因本文采用线性徐变理论，即徐变变化率与应变保持线性关系，且不考虑温度影响，因此C2=0，C3=1，C4=0。故徐变变形可表达为:

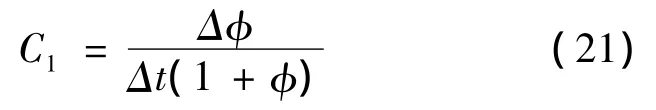
GL－1模型利用ANSYS的分析结果如表1所示，实测挠度与模拟挠度随时间的变化见图4。

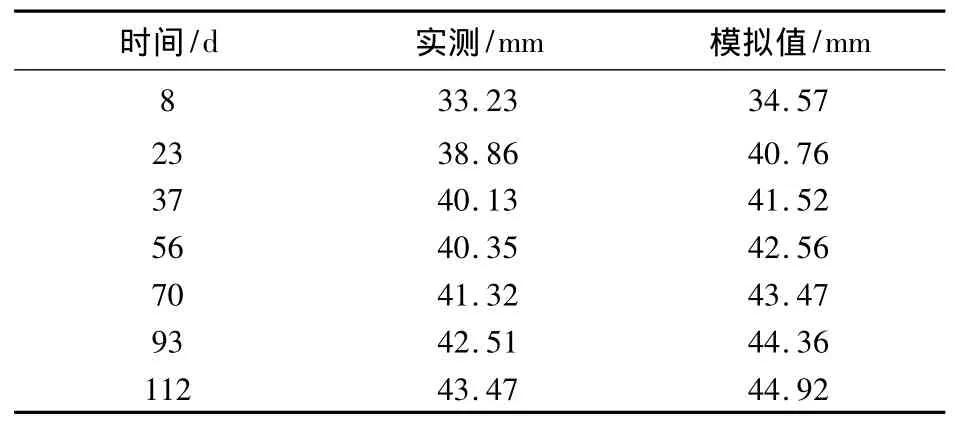
表1 GL－1的挠度计算结果比较Table1 Comparison between test values and simulated values of GL－1

表2 SCB－1的长期挠度变形Table 2 Long－term deflection of SCB－1

图2 GL－1有限元模型Fig.2 Finite element model of GL －1

图3 SCB－1有限元模型Fig.3 Finite element model of GL －1

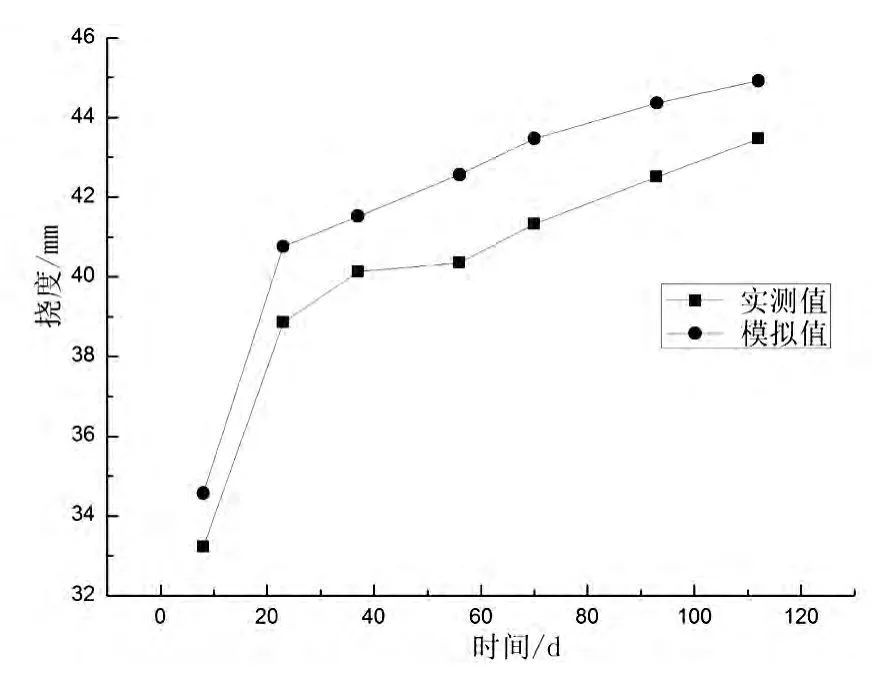
图4 GL－1梁实测挠度与模拟挠度随时间变化曲线Fig.4 Test and simulated curves for GL －1

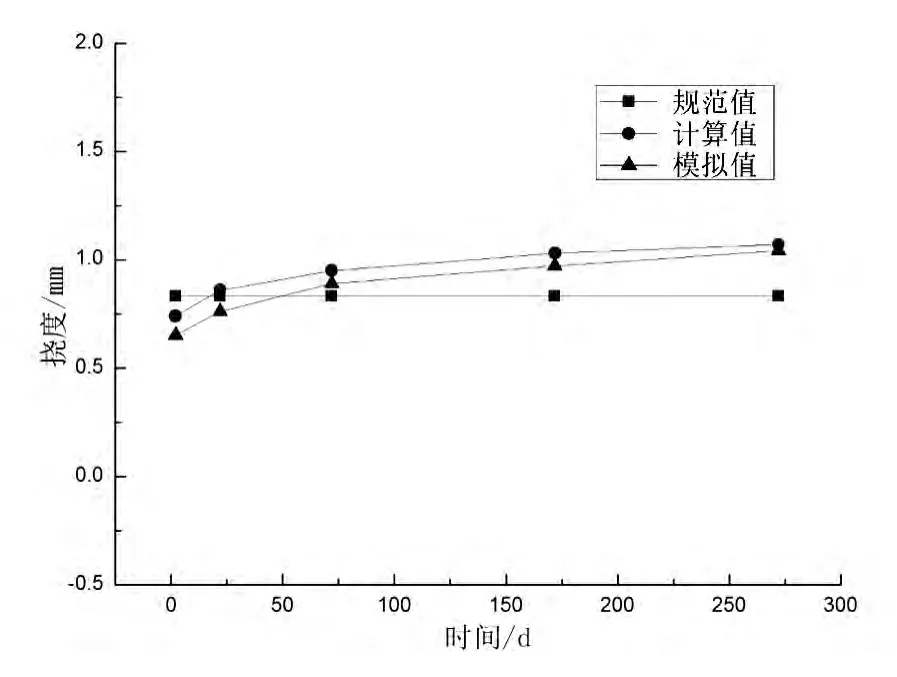
图5 SCB－1梁实测挠度、计算挠度与模拟挠度随时间变化曲线Fig.5 Comparison of simulated values，calculated values by suggested formula and design code for SCB－1

由图4可以看出:计算值和模拟值均大于实测值，且计算值和模拟值相差较小，因此可利用ANSYS对组合箱梁进行模拟分析。本文选用文献［10］的SCG－1进行公式验证。图3为SCB－1梁的有限元模型。由于跨中集中荷载作用下，组合箱梁挠度接近线性变化，因此本文仅考虑SCB－1梁在F=100 kN长期作用下的挠度变化情况，其中混凝土加载龄期为28 d，组合箱梁刚度按照组合箱梁的刚度计算公式计算。计算结果见表2，挠度随时间的变化曲线见图5。

由图5可以看出:组合箱梁的跨中挠度逐渐增大，且在加载初期增长较快，然后随着时间的推移，增长速率逐渐减慢，并趋于平缓。

比较本文公式的计算结果与按规范公式的计算结果，SCB－1梁大约加载20 d即可达到按规范公式的计算结果，因此规范公式的计算结果并不能准确反映组合箱梁的跨中挠度随时间的变化趋势。

4 结论

1)《钢结构设计规范》(GB50017－201X)送审稿初稿采用等效模量法近似考虑徐变效应，采用换算截面法计算组合梁的长期变形，通过计算可以看出，该方法得到的计算值偏小，进行长期荷载作用下组合梁的变形计算时偏于不安全。本文考虑加载龄期、荷载持续时间等对徐变的影响，从理论出发，推导出钢－混凝土组合箱梁考虑徐变时的挠度计算公式。

2)文献［6］的模拟值和实测值的比较证明了有限元建模的可行性，进而对文献［10］中的SCB－1梁进行有限元分析，并比较按照本文公式计算的挠度值和有限元模拟值，研究结果表明，按照本文公式可以方便计算出钢－混凝土组合箱梁在任意加载时间的挠度。公式形式简单，应用方便。

［1］GB/50017－201X，钢结构设计规范送审稿初稿［S］.

GB 50017－201X，Draft code of design of steel structure［S］.

［2］JTJ025－86，公路桥涵钢结构及木结构设计规范［S］.

JTJ025－86，Code for design of steel structure and wood structure of highway bridges and culverts［S］.

［3］余志武，张大付，焦娇.钢－混凝土连续组合箱梁负弯矩区极限抗弯承载力研究［J］.铁道科学与工程学报，2014，11(2):1 －6.

YU Zhiwu，ZHANG Dafu，JIAO Jiao.Research on ultimate flexural bearing capacity of negative moment area for steel－ concrete composite continuous box girder［J］.Journal of Railway Science and Engineering，2014，11(2):1－6.

［4］聂建国.钢－混凝土组合梁长期变形的计算与分析［J］.建筑结构，1997，27(1):42 －45.

NIE Jianguo.Long－term deformation calculation and analysis of steel－ concrete composite beam［J］.Building Structure，1997，27(1):42 －45.

［5］王骅.考虑收缩徐变的钢－混凝土组合梁变形计算［J］.长沙大学学报(自然科学版)，2004，24(1):56 －60.

WANG Ye.Deformation calculation of steel－ concrete composite beam considering shrinkage and creep of concrete［J］.Journal of Changsha University(Natural Science Edition)，2004，24(1):56 －60.

［6］李达.考虑荷载长期作用时型钢－混凝土组合梁的变形［J］.北京科技大学学报，2007，10(29):980 －984.

LI Da.Deformation of steel－ concrete composite beam considering long － term effect［J］.Journal of Beijing Science and Technology，2007，10(29):56 －61.

［7］汪磊.反复荷载作用下部分预应力混凝土梁桥长期挠度计算研究［J］.公路，2011(6):56－61.

WANG Lei.Long－term deformation calculation of partial pretressed concrete beam bridge under repeated loading［J］.Highway，2011(6):56 －61.

［8］AISC－LRFD，Load and resistance factor design specification for structural steel building［S］.3rd Edition.AISC，Chicago，IL，December，1999.

［9］Owens G W，Knowles P R，Dowling P J.Steel designers manual［M］.The Steel Construction Institute.5th ed.Cambridge:Blackwell Science Ltd，1992.

［10］李晓静.钢－混凝土组合箱梁疲劳性能研究［D］.长沙:中南大学，2014.

LI Xiaojing.Research of the fatigue performance of the steel－ concrete composite box beam［D］.Changsha:Central South University，2014.

［11］In Hwan Yang.Uncertainty and updating of long－term predication of prestress forces in PSC box girder bridges［J］.Computers and Structures，2005(27):1820 －1827.

［12］周凌宇.钢－混凝土组合箱梁受力性能及空间非线性分析［D］.长沙:中南大学，2004.

ZHOU Lingyu.Mechanical properties and spatial nonlinear analysis of steel－concrete composite box－beams［D］.Changsha:Central South University，2004.

［13］卢彭真.钢－混凝土组合箱梁空间分析理论与应用研究［D］.成都:西南交通大学，2009.

LU Pengzhen.Analysis theory and application research on the steel－concrete composite box beam［D］.Chengdu:Sichuan Southwest Jiao Tong University，2009.

［14］周旺保.钢－混凝土组合箱梁及其框架结构的静动力性能分析［D］.长沙:中南大学，2013.

ZHOU Wangbao.Static and dynamic performance analysis of steel－concrete composite box beam［D］.Changsha:Central South University，2013.

［15］胡夏闵，薛伟，曹雪娇.钢－混凝土组合梁挠度计算的附加曲率法［J］.建筑结构学报，2010(增刊):385－389.

HU Xiamin，XUE Wei，CAO Xuejiao.Additional curvature method in calculation of deflection of steel－concrete composite beam［J］.Journal of Building Structure，2010(Suppl.):385 －389.

［16］王恩来.钢－混凝土组合梁的长期性能研究［D］.长沙:中南大学，2009.

WANG Enlai.Long－term performance of steel－concrete composite box beam［D］.Changsha:Central South University，2009.

［17］Desi L，Leomi G，Trarantio A M.Time－dependent analysis of prestressed composite beams［J］.J Struct Div，ASCE，1995，121(4):621 －633.

［18］宋玉普.混凝土结构的疲劳性能及设计原理［M］.北京:机械工业出版社，2006.

SONG Yupu.Fatigue behavior and design principle of concrete structures［M］.Beijing:China Machine Press，2006.

［19］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007.

WANG Xinmin.Numerical analysis of engineering structure by ANSYS［M］.Beijing:China Communications Press，2007.

［20］方恺.弯矩作用下考虑连接件刚度的钢－混凝土组合梁有限元模型研究［D］.上海:同济大学，2003.

FANG Kai.Research of finite element model of steelconcrete composite beam under the action of bending moment in consideration of stiffness of shear connector［D］.Shanghai:Tongji Univerity，2003.

［21］周凌宇，贺桂超.大跨度开口钢－混组合箱梁有限元参数分析［J］.铁道科学与工程学报，2012，9(1):5－11.

ZHOU Lingyu，HE Guichao.Parametric analysis of long－span steel－ concrete composite beam［J］.Journal of Railway Science and Engineering，2012，9(1):5－11.

［22］陶慕轩，聂建国.预应力钢－混凝土连续组合梁的非线性有限元分析［J］.土木工程学报，2011，44(2):8－20.

TAO Muxuan，NIE Jianguo.Nonlinear finite element analysis of prestressed steel－concrete continuous composite beam［J］.China Civil Engineering Journal，2011，44(2):8－20.

［23］惠荣炎，黄国兴，易冰若.混凝土的徐变［M］.北京:中国铁道出版社，1988.

HUI Rongyan，HUANG Guoxing，YI Bingruo.Creep of concrete［M］.Beijing:China Railway Press，1988.