可变模糊优选模型的反TBM战斗部研制风险综合评价

韩晓明，陈俊杰，南海阳

（空军工程大学防空反导学院，西安710051）

可变模糊优选模型的反TBM战斗部研制风险综合评价

韩晓明，陈俊杰，南海阳

（空军工程大学防空反导学院，西安710051）

依据反TBM导弹战斗部研制的特点，建立了反TBM战斗部研制风险综合评价指标体系。引入了效用函数对定量评价指标进行统一量化，采用专家评估法对定性指标进行了量化。在此基础上，提出了一种基于可变模糊优选模型的反TBM导弹战斗部研制风险综合评估方案，该模型通过计算各方案的测度并进行比较，实现对战斗部研制风险方案的优劣性的综合评价，通过算例分析，验证了模型的合理性。

战斗部，可变模糊优选模型，评价，反TBM导弹

0 引言

随着来自空中战术弹道导弹（TBM）的威胁不断升级，作为最有效的防御武器——反TBM导弹，得到了各国军事界的高度重视和大力发展，同时也对其提出了更高的要求［1］。反TBM战斗部是反TBM导弹的杀伤装置，它的研制已成为一项耗资巨大的复杂系统工程，在研制的过程中存在着极大的风险。然而，反TBM战斗部研制风险评价所涉及的因素较多、范围较广，属于多目标决策问题，如何在众多的研制方案中作出准确的评价，是研究部门面临的重要课题。因此，对反TBM战斗部研制风险进行综合评价具有非常重要的意义。

1 反TBM战斗部研制风险综合评价指标体系

进行反TBM战斗部研制风险评价的目的，是为了节省研制阶段的各种资源，以便在反TBM战斗部的寿命周期各阶段进行权衡，在各反TBM战斗部型号之间进行比较，从而判断进行研制的必要性。因此，在反TBM战斗部型号发展论证阶段，对战斗部的研制风险进行分析具有重要的意义。

1.1 反TBM战斗部研制风险

在反TBM战斗部的研制中，由于采用了新技术、新材料等，不可避免地会有一些不可预知因素的影响，从而会造成一些不希望事件的发生，如技术上难以解决的问题、性能上不能完全满足指标要求、计划费用的超支、预计研制进度的延误等。反TBM战斗部研制风险评价可以使研制方对战斗部各分系统及总体系统的风险有一个清醒的认识，从而为方案选择及研制风险的管理和控制提供基础［2］。

1.2 反TBM战斗部研制风险评价指标体系

对反TBM战斗部研制风险进行综合评价，采用不同的准则，分析的结果也会不同。本文依据指标体系构建原则（系统性原则、简明性原则、客观性原则、时效性原则），综合考虑反TBM战斗部的发展、特性及组成等因素，并参阅大量相关文献和征求专家的意见后，把反TBM战斗部的研制风险分为立项风险、技术风险、人力风险、社会环境风险、管理风险五大类，进一步对以上五类风险进行细分，构建出反TBM战斗部研制风险综合评价指标体系，如图1所示［3-5］。

图1 反TBM战斗部研制风险综合评价指标体系

2 基于可变优选模型的反TBM战斗部研制风险综合评价

反TBM战斗部研制风险的评价是具有一定程度的不确定性，因为反TBM战斗部研制的风险因素是模糊的。由于主观的原因，人们对某些影响因素的褒贬程度不尽相同，很难直接用统计学的方法确定这些因素的具体判断值。因此，如何对不确定信息资料进行量化处理和综合评价就显得特别重要。本文认为利用模糊优选模型对武器装备研制项目风险进行综合评价有其科学性和更强的实用价值。

2.1 可变优选模型［6］

设有待聚类的n个样本组成的集合：{x1，x2，…，xn}，用m个指标特征值向量（x1j，x2j，…，xmj）对样本进行聚类，则有指标特征值矩阵

xij为样本j指标i的特征值，i=1，2，…，m；j=1，2，…，n。

由于m个聚类指标特征值物理量纲不同，需要对指标特征量进行规格化。即要将指标特征值xij变换为对聚类样本关干模糊概念A趋的指标相对隶属度rij。在模糊聚类中通常有两类指标：

（1）越大越优效益型指标，即指标特征值越大，聚类类别排序越前，其规格化公式为

（2）越小越优成本型指标，即指标特征值越小，聚类类别排序越前，其规格化公式为：

则指标特征值矩阵变换为指标对模糊概念的相对隶属度矩阵，即指标特征值规格化矩阵：

设n个样本依据m个指标特征值规格化数按c个类别进行聚类，其模糊聚类矩阵为

uhj为样本j隶属于类别h的相对隶属度，h=1，2，…，c；j=1，2，…，n。满足条件

类别h的m个指标特征值规格化数表示了h类的聚类特征，在模糊聚类中通常称为聚类中心，则c个类别的聚类特征可用m×c阶模糊聚类特征（聚类中心）矩阵

表示，sih为类别h指标i的聚类特征规格化数，i=1，2，…，m；h=1，2，…，c。

考虑不同指标对聚类的影响不同，引入指标权向量

满足：

2.2 可变模糊模式识别模型

设有待识别的n个样本组成样本集，依据m个指标i的特征值，按已知c个级别指标标准值模式对样本进行识别，其指标特征值与指标标准特征值矩阵分别为

由于指标特征值、指标标准特征值量纲不同，需要对其进行规格化处理，通常指标分为：①递增型（越小越优或成本型），即由1级至c级指标标准特征值递增；②递减型（越大越优或效益型），即由1级至c级指标标准特征值递减。越小越优、越大越优型指标与指标标准特征值的规格化公式分别为

模糊识别模型：

2.3 可变模糊优选模型

如果将c级识别简化为2级识别，a、p的4种组合分别对应着目前国内外4种不同的优选决策（或评价）模型，此时c=2，aj=1，bj=3，则可变模糊模式识别模型简化为

当si1=1，si2=0，h=1得样本j对1级（优级）的相对隶属度

当h=2，则样本j对2级（劣级）得相对隶属度

根据式（15）、式（16）有：

式（15）、式（16）满足可变模糊集的对立模糊集定义，应用中只需求解对1级（优级）的相对隶属度即可。

（1）令a=1，p=1，由于海明距离为绝对值距离，，式（15）变为模糊综合评判模型

（2）令a=1，p=2，式（15）变为TOPSIS理想点模型

（3）令a=2，p=1，式（15）变为描述神经网络系统中神经元的激励函数模型

（4）令a=2，p=2，式（15）变为模糊优选模型

这里由式（17）～式（20）表示的u1j、u2j、u3j、u4j的含义为：由（1）～（4）组模型参数求得的相对优属度。

2.4 评价指标的归一化

2.4.1 指标重要性一致性排序［7-9］

目标集中的元素pk与pl作二元比较，若（1）pk比pl重要，则排序标度ekl=1，elk=0；（2）pk比pl同样重要，则排序标度ekl=0.5，elk=0.5；（3）pl比pk重要，则排序标度ekl=0，elk=1。其中k=1，2，…，m；l=1，2，…，m。

设系统有目标集关于重要性的二元比较矩阵：

式中：ekl仅在0，0.5，1中取值、ekl+elk=1、ekl+elk=1，E称为目标集二元比较重要性排序标度矩阵。

2.4.2 定性指标的量化处理

根据指标的重要性排序，运用专家的经验与知识作出二元比较判断，应用模糊语气算子与模糊标度相对隶属度关系表得到指标的非归一化权向量。

对重要性的相对隶属度进行归一化，得到目标集的全向量：

表1 模糊语气算子与模糊标度、相对隶属度关系表

式中：β1i为排序第1位目标与第i位目标关于重要性的二元比较模糊标度值。

3 算例及分析

3.1 原始数据

以某型反TBM导弹战斗部研制风险方案综合评价和优选为例，由专家提出了5种备选的方案，。现有A，B，C，D，E5种研制方案，对其立项、技术、人力、社会环境和管理5个技术指标的风险等级进行评估。通过问卷调查，实施专家0—1打分法，得到表2所示的原始数据表［2］。

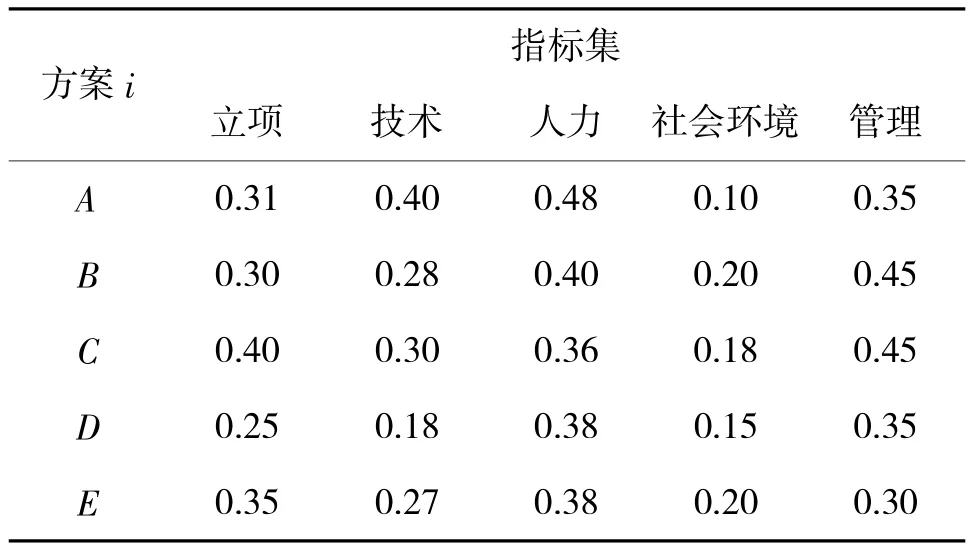
表2 反TBM导弹战斗部风险研制方案

3.2 确定指标相对隶属度矩阵

根据表2中5项指标中都是越小越优型指标，根据公式对5项指标进行规格化，得到指标相对隶属度矩阵：

3.3 指标的重要性排序一致性标度矩阵

根据矩阵F的重要性排序。运用经验知识。以排序为（1）的指标，逐个地与排序为其他序号的指标，作出重要性程度的二元比较判断。根据以上运用专家的经验与知识作出的二元比较判断。应用表1得到5项指标的非归一化权向量

则归一化后指标权向量为

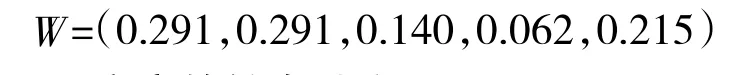
3.4 研制方案的综合排序

令a=1，p=1，应用模糊综合评价模型解得的方案相对优属度向量为：

令a=1，p=2，应用模型TOPSIS理想点模型解得的方案相对优属度向量为：

令a=2，p=1，应用神经网络系统中神经元激励函数模型解得的方案相对优属度向量为：

令a=2，p=2，应用模糊优选模型解得的方案相对优属度向量为：

以上4组参数的均值为：

这样得到的排序结果，通过比较综合测度可得反TBM战斗部研制风险方案的最终排序（由优到劣）为：方案D＞方案E＞方案B＞方案A＞方案C，无论从理论分析或者是与其他方法比较都是合理而可信的。

4 结束语

本文在对国内外典型研制风险方案评价方法分析的基础上，建立了基于可变模糊优选模型的研制风险综合评价模型。利用越小越优成本性进行规格化得到指标相对隶属度指标重要性排序一致性和归一化处理得到评价指标的聚类权重，在此基础上通过模糊综合评价模型、理想点模型、神经网络系统中神经元激励函数模型和模糊优选模型相结合确定和计算研制方案的评价与优选排序。经实例验证，利用可变模糊优选模型进行研制风险的评价，减少了人为因素的作用，所选方法思路清晰、简单易用，适合用于反TBM战斗部研制风险的评价决策，提出了一种综合评价反TBM战斗部研制风险的新方法。

［1］李静海.防空导弹战斗部性能分析及发展趋势［J］.地面防空武器，2005（1）：25-28.

［2］姜科.防空反导导弹战斗部研制方案评价模型研究［D］.西安：空军工程大学，2011.

［3］徐学华，徐翔.弹药系统工程基础［M］.北京：兵器工业出版社，2006.

［4］吕惠文，张炜，王铭坤.大型装备研制风险管理及对策［J］.四川兵工学报，2014，33（12）：52-55.

［5］Gu X H，Cao B.The Synthetic Evaluation of Warhead Overall Efficiency［J］.Journal of Systems Engineering and Electronics，2003，14（1）：12-17.

［6］陈守煜.可变模糊集理论与可变模型集［J］.数学的实践与认识，2008，38（18）：31-34.

［7］陈守煜.可变模糊集理论与模型及其应用［M］.大连：大连理工大学出版社，2009.

［8］Jiang K，Liu T，Zhang L，et al.Research of the Optimal Estimation Model of the Equipment Development Cost Engineering Method［C］//Proc.of International Conference on Engineering and Business Management.USA：Scientific Research Publishing Press，2010.

［9］晁殿雷，韩晓明，张帆.导弹武器系统研制阶段风险评估模型［J］.火力与指挥控制，2010，35（3）：61-64.

Synthetic Evaluation for Developing Risk of Anti-TBM Warhead Based on Variable Fuzzy Optimization Model

HAN Xiao-ming，CHEN Jun-jie，NAN Hai-yang
（School of Air and Missile Defense，Air Force Engineering University，Xi’an 710051，China）

According to the development characteristics of anti-TBM warhead，the comprehensive evaluation index system of anti-TBM warhead development risk is established.Quantitative index will be uniformly quantified by introducing utility function，the qualitative index with Expert evaluation method is established.On the basis of it，a model of synthetic evaluation for developing risk of anti-TBM warhead is put forward based on the variable fuzzy optimization model，which realize the evaluation for the superior and interior of developing plan by calculating and comparing the measure of all plans.The accuracy of the model is proved through an example.

warhead，variable fuzzy optimization model，evaluation，anti-TBM missile

TN958

A

1002-0640（2015）12-0084-05

2014-11-05

2015-01-15

韩晓明（1961-），男，陕西渭南人，教授。研究方向：装备管理与决策。