最短路径算法并行化策略的研究与实现

（武汉外国语学校，湖北武汉，430000）

最短路径算法并行化策略的研究与实现

闵思晗,付逸飞

（武汉外国语学校，湖北武汉，430000）

现阶段，随着我国智能交通系统与通信系统的不断发展完善，网络新特性的出现，对于网络中最短路径问题研究具有非常重要的意义。本文主要选取几种最短路径标号串行算法，并在此基础上分别通过网络复制与网络分割策略，对其最短路径进行求解，从而实现最短路径算法并行策略的研究。

最短路径算法；并行计算；网络复制；网络分割

最短路径算法是实现资源分配与路线设计优化的基础，随着信息科技的不断完善与发展，现阶段网络最短路径算法越来越多，不同的网络环境与应用，需求具有不同特性的最短路径算法，并行计算技术的不断发展为节省计算时间提供了有效的计算路径，不断提高了交通网络最短路径问题的解决效率，实现大规模交通网络最短路径问题的解决。

图1：有向图G=(V,A)

1 最短路径算法比较分析

1.1 标号算法

标号算法在目前的最短路径算法中，占有非常重要的地位，它可以依照不同的节点，对策略进行相应的分析与处理。

例如图一中的有向图G=(V,A)，将节点1作为图中的源点，常用的标号算法主要是指在该图中，求解单个源点到其它各个源点的最短路径，如该图1所示，在建立过程中，每一个独立的节点都具有不同信息分类，例如长度标号,父节点号及节点的当前状态.

在迭代过程中，源点至节点的最短路径中的上限值，主要在长度标号中保留，在最短路径计算结束之时，长度标号成为该线路中唯一最短的路径；在该有向图中，其中位于节点之上的上一层节点标号，在父节点中保存；节点的当前状态中的数值主要代表，其未访问以及永久标号等状态。

1.2 最具代表性的最短路径标号算法的选取

现阶段，我国对最短路径算法的研究已逐渐趋于成熟，但目前多种多样的最短路径算法，在测试网络中的效率以及各项性能都不完善，在本文中最短路径标号算法的选取中，主要选取几种具有代表性的算法来实现计算与求解。Bellman-Ford-Moore(BFM)（LC-1q）,D' Esopo-Pape（LC-2q），以及Dijkstra算法（LS）。

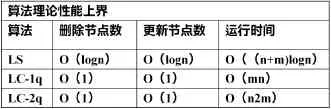
表一：三种最短路径串行算法理论时间复杂性

这三种算法的性能理论具有相应差别，虽然LC算法，理论上的复杂性上界比较大，但在稀疏网络中具有良好的应用性能，由于其自身的应用特性，因此人们对于其期望性能的预测，存在很大的困难性，但与之相反，LS具有良好的预测性。

2 最短路径算法并行化策略的研究

2.1 网络复制策略

在求解最短路径的过程中，可以利用系统的主处理器，将网络复制于各处理器中，网络源点按照处理器个数进行相应划分，并将其分配于各处理器中；之后各个处理器，将不同源点所计算出的不同最短路径，发送至主处理器，进而实现对其的分析与整理。

在对各处理器中的不同源点进行分配时，应根据其间的计算负载平衡，对其进行平均分配，在对源点最短路径进行计算时，各个处理器间不用进行信息的互换，因此一定程度上节省了所需时间，提高了工作效率。

2.2 网络分割策略

网络分割最短路径算法，主要是指在分布式网络中实现单源最短路径的解决，在工作过程中，它首先可将系统中的整体网络划分为多个子网，同时将其均匀分配至各处理器中。在该网络分割系统中，包括边界节点以及内部节点，它们都是系统的重要组成部分，在该算法实施当中，必须要保持各处理器间的部分通信畅通。在利用该方法进行最短路径求解的过程中，需要对边界节点的标号进行系统的更新，在对其进行更新时，还应该将其整理成相应的消息，并将其发送给相邻子网中的处理器，由该处理器对其进行计算。

2.2.1 网络分割

在网络分割时应该注意尽量的将边界节点的数量降到最低，这样可节省开支，同时对于子网中的负载量应使其趋于平衡，这样才能尽量减少处理器在工作时的时间，提高其工作效率。交通网络中可采用模拟退火算法，而随机网格可以采用方形分割法。

模拟退火算法在算法中可以解决大规模的组合优化问题，可以有效解决最短路径计算问题。具体算法如下所示：本文以边界节点量与子网节点量间的方差建立函数（p代表分割后的子网数，nbi代表在第i个子网中所包含的边界节点的个数，nb则代表总边界节点数）

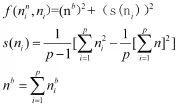
由以上公式可以得出在模拟退火算法方法中，当函数值达到最小时，各边界节点与子网中节点数值差距较小，因此其可以最大化的满足网格分割要求。

2.2.2 终止检测分析

在利用并行标号算法的网格分割求解最短路径时，其消息的转换与交流，会造成时间的过度消耗，同步过程也会造成时间的损耗。终止检测频率，对计算途中的各个处理器的等待时间有很大影响，在本文终止检测方法的选取中，主要采用令牌传递法，该方法不需对最优终止检测频率进行预测。

3 最短路径算法分析

本实验中主要采用并行函数库编程，实现对最短路径的计算，同时在计算过程中，利用6台节点机实现对算法加速比以及其效率的检验，在测试网络的选取中，主要应用了3个实际的道路网格以及3个随机网格，在稀疏性质中保证二者的相似性，同时添加内部节点与边缘节点之间的连接弧，从而使二者的特征更加相似。

算法加速比：本文采取的算法模式都属于粗粒度并行算法。在此基础下可以看出网络复制策略以及网络分割策略都有很好的加速比，同时LC与LS综合比较，以由于串行算法自身的标点节点的选取以及删除等造成的影响，使得LC的整体加速比优于LS，因此从而证实LC比LS更适用于并行化。两种策略下运用机器以及相关源点对最短路径加速比进行分析。

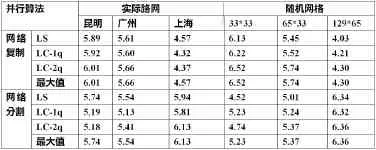
表二：两种策略最短路径并行加速比

根据上述表格变化趋势分析，在实际路网以及随机网格中，网络复制加速比会随着节点数的增加而变小，而网络分割中其加速比会随网络规模的不断增大而增大。因此说明大规模交通网中网络分割比网络复制并行算法更具有优越性。

算法可拓展性：两种并行算法都具有很好的可拓展性，在网络复制中，网络规模越小其扩展性越好，在网格分割中则恰恰相反，因此证实了网络分割，较适用于大规模网络最短路径求解。

4 结束语

综上所述，现阶段，我国对于最短路径算法并行化策略的研究已逐渐趋于完善，对于最短路径的算法也具有多种多样性，本文在研究中主要选取了几种效率较高的串行最短路径标号算法，同时利用网络复制与分割策略对其进行应用，从而进一步提升其计算效率，为交通运输中最短路径并行算法的选择与应用提供相应的依据。

[1] 孙文彬,谭正龙,王江,周长江,何俊芳.最短路径算法的并行化策略分析[J].地理与地理信息科学,2013,04:17-20.

[2] 卢照.基于城市路网最短路径并行搜索算法的研究[D].陕西师范大学,2010.

[3] 郭绍忠,王伟,周刚,胡艳.基于GPU的单源最短路径算法设计与实现[J]. 计算机工程,2012,02:42-44.

[4] 张钟.大规模图上的最短路径问题研究[D].中国科学技术大学,2014.

Research and implementation of the parallel strategy of shortest path algorithm

Min Sihan,Fu Yifei
(Wuhan foreign language school,Wuhan,Hubei,430000)

At present,with the continuous development of the intelligent transportation system and communication system in our country,the emergence of the new features of the network is very important for the research of the shortest path problem in the network.In this paper,we select some of the shortest path label serial algorithm,and on this basis,respectively,through the network replication and network segmentation strategy,the shortest path to solve the problem,so as to achieve the shortest path algorithm parallel strategy.

shortest path algorithm;parallel computing;network replication;network partition

闵思晗（1998-），女，武汉外国语学校高三在读，

付逸飞（1999-），男，武汉外国语学校高二在读